$2S=2+\frac{3}{2^1}+...+\frac{2007}{2^{2005}}$
$\Rightarrow S=2S-S=2-(\frac{1}{2^1}+\frac{1}{2^2}+...+\frac{1}{2^{2005}})-\frac{2007}{2^{2006}}$
$\Leftrightarrow S=3-\frac{2009}{2^{2006}}<3.$

Vậy bạn có thể tự nghĩ được ko? Nếu cứ nhờ người khác giải thế này thì bao giờ mới khá lên được.
Xét $A=x^0+x^1+x^2+...+x^n$
$\Rightarrow x.A=x^1+x^2+x^3+...+x^n+x^{n+1}$
$\Rightarrow x.A-A=(x-1)A=x^{n+1}-x^0$
$\Rightarrow A=\frac{x^{n+1}-1}{x-1}$ với điều kiện $x$ khác $1$.

Không ai làm à, vậy mình xin phép làm mấy bài:
3, PT đã cho tương đương với:
$(x+1)(x^{2}+1)=y^{2}=y.y=y^{0}.y^{2}$
Đến đây chắc là ra rồi.

Bài này nếu $y^2$ còn ước khác thì sao?

$2. x^2+y^2=6(a^2+b^2) (1)$
$\Rightarrow 3|x^2+y^2$
$\Rightarrow 3|x^2$ và $3|y^2.$ (cái này chắc dễ chứng minh nhỉ )
$\Rightarrow 3|x$ và $3|y.$
Đặt $x=3x_1; y=3y_1.$
$(1)\Leftrightarrow 3(x_1^2+y_1^2)=2(a^2+b^2)$
Vì $(2;3)=1\Rightarrow 3|a^2+b^2.$ Tương tự như trên, cũng rút được $a=3a_1;b=3b_1.$
Giờ pt trở thành $x_1^2+y_1^2=6(a_1^2+b_1^2)$
Mời bạn làm tiếp.

Mở rộng 1: Ta sẽ thử mở rộng số mũ của x,y,z:
Cho $x,y,z$ thỏa mãn $x^{2n}+y^{2n}+z^{2n}=\frac{1-16(xyz)^n}{4}.$
Tìm GTNN của $A=\frac{x^n+y^n+z^n+4(xyz)^n}{1+4[(xy)^n+(yz)^n+(zx)^n]}.$

Ta nhận thấy nếu đặt $x^n=a; y^n=b; z^n=c$ thì quay trở về bài toán ban đầu.

Bài làm của daovuquang:
Bổ đề 1: $x,y,z>0$ cmr $x+y+z\geq 3\sqrt[3]{xyz}$ $(1)$
Chứng minh: Đặt $x=a^3,y=b^3,z=c^3.$ Khi đó $(1) \Leftrightarrow a^3+b^3+c^3-3abc\geq 0 \Leftrightarrow (a+b+c).\frac{1}{2}\left[(a-b)^2+(b-c)^2+(c-a)^2\right]\geq 0$
Hiển nhiên do $x,y,z>0 \Rightarrow a,b,c>0$ và $\dfrac{1}{2}\left[(a-b)^2+(b-c)^2+(c-a)^2\right]\geq 0$ dấu $=$ khi $a=b=c \Rightarrow x=y=z$
Bổ đề 2: $x^2+y^2+z^2\geq xy+yz+zx$
Chứng minh: Biến đổi tương đương ta được $\frac{1}{2}[(x-y)^2+(y-z)^2+(z-x)^2]\geq 0.$
Dấu $"="$ xảy ra khi $x=y=z.$
Áp dụng 2 bổ đề trên vào bài, ta được $A\geq \dfrac{3\sqrt[3]{xyz}+4xyz}{1+4(x^2+y^2+z^2)}$ $(2)$
Mặt khác $x^2+y^2+z^2=\dfrac{1-16xyz}{4}(gt)$
Thay vào $(2)$ suy ra $A\geq \dfrac{3\sqrt[3]{xyz}+4xyz}{1+4(x^2+y^2+z^2)}=\dfrac{3\sqrt[3]{xyz}+4xyz}{1+4\left(\frac{1-16xyz}{4}\right)}=\dfrac{3\sqrt[3]{xyz}+4xyz}{2(1-8xyz)}$
Đặt $\sqrt[3]{xyz}=k$
Suy ra $A\geq \dfrac{3k+4k^3}{2(1-8k^3)}$
Mặt khác nhận thấy từ điều kiện $x^2+y^2+z^2=\dfrac{1-16xyz}{4} \Rightarrow 4(x^2+y^2+z^2)+16xyz=1$
$1=4(x^2+y^2+z^2)+16xyz\geq 12\sqrt[3]{x^2y^2z^2}+16xyz$ (áp dụng bổ đề)
$\leftrightarrow 12\sqrt[3]{x^2y^2z^2}+16xyz-1 \le 0 \Rightarrow 12k^2+16k^3-1\le 0 \Rightarrow \left(k-\dfrac{1}{4}\right).\left(k+\dfrac{1}{2}\right)^2\le 0$
Do đó $k-\dfrac{1}{4}\le 0$ (do $\left(k+\dfrac{1}{2}\right)^2\geq 0$)
$\Leftrightarrow k\le \dfrac{1}{4}$ mà $x,y,z>0 \Rightarrow 0<k\leq\dfrac{1}{4}$
Như vậy $A\geq \dfrac{3k+4k^3}{2(1-8k^3)}$ với mọi $0<k\le \dfrac{1}{4}$
Suy ra $A\geq max\left(\dfrac{3k+4k^3}{2(1-8k^3)}\right)$ với $0<k\le \dfrac{1}{4}$ (ta làm được điều này do $0<k\le \dfrac{1}{4}$ là tập xác định)
Ta sẽ chứng minh $max\left(\dfrac{3k+4k^3}{2(1-8k^3)}\right)=\dfrac{13}{28}$
$\Leftrightarrow 28(3k+4k^3)\le 26(1-8k^3)$
$\Leftrightarrow 320k^3+84k-26\le 0$
$\Leftrightarrow 2(4k-1)(40k^2+10k+13)\le 0$
$\Leftrightarrow (4k-1)\le 0$ (do $40k^2+10k+13=40(k^2+\dfrac{1}{4}k+\dfrac{13}{40})=40[(k+\dfrac{1}{8})^2+\dfrac{99}{320}]>0$
$\Leftrightarrow k\le \dfrac{1}{4}$ đúng do ta đã cm trên
Suy ra $max\left(\dfrac{3k+4k^3}{2(1-8k^3)}\right)=\dfrac{13}{28} \Rightarrow A\geq \dfrac{13}{28}$
Dấu $=$ khi $x=y=z$ và $k=\sqrt[3]{xyz}=\dfrac{1}{4} \Rightarrow x=y=z=\dfrac{1}{4}$

Lại là xét hàm nữa đây mà
Mở rộng không đc công nhận
D-B=38h
E=10
F=0
S=40

Bài làm của daovuquang:
Viết lại hệ pt:\[
\left\{ \begin{array}{l}
2x\left( {y^2 + a^2 } \right) = y\left( {y^2 + 9a^2 } \right)(1) \\
2y\left( {z^2 + a^2 } \right) = z\left( {z^2 + 9a^2 } \right)(2) \\
2z\left( {x^2 + a^2 } \right) = x\left( {x^2 + 9a^2 } \right)(3) \\
\end{array} \right.
\]
Dễ thấy $x=y=z=0$ là nghiệm của pt. Dưới đây ta chỉ xét $x,y,z\neq 0.$
Xét $2x(y^2+a^2)=y(y^2+9a^2).$
$\Rightarrow \frac{2x}{y}=\frac{y^2+a^2}{y^2+9a^2}.$
Nhận xét: $VP\geq 0\Rightarrow VT\geq 0\Rightarrow x,y$ cùng dấu.
Tương tự, $y,z$ cùng dấu$\Rightarrow x,y,z$ cùng dấu.
TH1: $x,y,z>0$
Giả sử $x=max{x;y;z}$.
Xét $2x(y^2+a^2)=y(y^2+9a^2).$
Vì $x\geq y$ nên $2y^2+2a^2\leq y^2+9a^2$
$\Leftrightarrow y^2\leq 7a^2\Leftrightarrow y\geq \sqrt{7}a.$
Ta xét tiếp $2z(x^2+a^2)=x(x^2+9a^2)$
Vì $x\geq z$ nên $2x^2+2a^2\geq x^2+9a^2$
$\Leftrightarrow x\geq \sqrt{7}a(4).$
Quay trở lại $(1)$, ta thấy $(1)\Leftrightarrow x=\frac{y(y^2+9a^2)}{2(y^2+a^2)}.$
Ta sẽ chứng minh $\frac{y(y^2+9a^2)}{2(y^2+a^2)}\leq\sqrt{7}a$
$\Leftrightarrow y^2+9a^2y\leq2\sqrt{7}y^2+2\sqrt{7}a^3$
$\Leftrightarrow (\sqrt{7}-y)(y^2-\sqrt{7}y+2)\geq0.$
Nhận thấy BĐT cuối luôn đúng do $\sqrt{7}-y\geq\sqrt{7}-\sqrt{7}=0$ và $y^2-\sqrt{7}y+2=(y-\frac{\sqrt{7}}{2})^2+\frac{1}{4}\geq0.$
Suy ra $\frac{y(y^2+9a^2)}{2(y^2+a^2)}\leq\sqrt{7}a\Rightarrow x\leq\sqrt{7}a(5).$
Kết hợp $(4)$ và $(5)$, ta được $x=\sqrt{7}a.$
Thay vào $(1)$, ta được $y=\sqrt{7}a.$ Thay vào $(2)$, ta được $\Rightarrow z=\sqrt{7}a\Rightarrow x=y=z=\sqrt{7}a.$
TH2: $x,y,z<0$
Đặt $x=-m; y=-n; z=-p\Rightarrow m,n,p>0.$
Viết lại hệ pt:\[
\left\{ \begin{array}{l}
2m\left( {n^2 + a^2 } \right) = n\left( {n^2 + 9a^2 } \right)\\
2n\left( {p^2 + a^2 } \right) = p\left( {p^2 + 9a^2 } \right)\\
2p\left( {m^2 + a^2 } \right) = m\left( {m^2 + 9a^2 } \right)\\
\end{array} \right.
\]
Việc giải hệ này giống hệt như TH1$\Rightarrow$ pt có nghiệm $x=y=z=-\sqrt{7}a.$
Kết luận: $(x;y;z)=(0;0;0);(\sqrt{7}a;\sqrt{7}a;\sqrt{7}a);(-\sqrt{7}a;-\sqrt{7}a;-\sqrt{7}a).$


Em sai từ chỗ này

Xét $2x(y^2+a^2)=y(y^2+9a^2).$
$\Rightarrow \frac{2x}{y}=\frac{y^2+a^2}{y^2+9a^2}.$

Cho em 7 đ

D-B=25h
E=7
F=0
S=42

Em xin giải câu b:


Lấy $F$ là trung điểm $OC$. Kẻ đường trung bình $GL$ của $\triangle{ABC}$ ($GL // AB$ và $GL=\frac{1}{2}AB$)$\Leftrightarrow F$ là trung điểm $GL\Leftrightarrow FO=FC=FG=FL(1).$
Từ phần a lúc trước, ta được $\widehat{HXI}=90^o$ và $AI=CH\Leftrightarrow GI=GH$. Theo tính chất trung tuyến của tam giác vuông, ta được $GX=GI\Leftrightarrow \triangle{GXI}$ cân tại $G\Leftrightarrow \widehat{GXI}=\widehat{GIX}=\widehat{CIJ}(2).$
Tương tự, $\triangle{XLJ}$ cân tại $L\Leftrightarrow \widehat{LXJ}=\widehat{LJX}=\widehat{CJI}(3).$
Từ $(2),(3)\Leftrightarrow \widehat{GXL}=\widehat{GXI}+\widehat{LXJ}=\widehat{CIJ}+\widehat{CJI}=90^o$
$\Leftrightarrow \triangle{GXL}$ vuông tại $X$
$\Leftrightarrow XF=GF=FL(4).$
Từ $(1),(4)\Leftrightarrow FX=FO=FC\Leftrightarrow X$ sẽ chạy trên đường tròn tâm $F$ bán kính $FO.$

Hình vẽ:


Dễ thấy $AMBN$ là hình chữ nhật$\Rightarrow AN=BM$ và $AN // BM.$
Cộng thêm $IN // KB\Rightarrow \widehat{INA}=\widehat{KBM}.$
$\Rightarrow \triangle{AIN}=\triangle{MKB} (cgv.gn)$
$\Rightarrow AI=MK=HC.(1)$
Xét $\triangle{AIN}$ và $\triangle{HCJ}$ có:

$\left\{\begin{matrix}
AI=HC(cmt)\\
IN=CJ\\
\widehat{AIN}=\widehat{HCJ}
\end{matrix}\right.$
$\Rightarrow \triangle{AIN}=\triangle{HCJ}$
$\Rightarrow AN=HJ$ và $AN // HJ.$
Mặt khác từ $(1)$ và $AI // MK\Rightarrow AMKI$ là hình bình hành$\Rightarrow IK // AM.$
Dễ thấy $AN \perp AM\Rightarrow HJ \perp IK.$
Theo gt $KJ \perp AC\Rightarrow J$ là trực tâm $\triangle{HIK}\Rightarrow IJ \perp HK\Rightarrow$ đpcm.

Câu b mới chỉ giải phần thuận.
D-B=11.8h
E=8.5
F=0
S=61.7

Mở rộng 3: Ta thử mở rộng khoảng cách giữa $i,j$ và được bài toán sau:
Cho dãy $n$ số nguyên dương $a_1;a_2;...;a_n$ thỏa mãn tính chất sau: với mọi phần tử $a_i;a_j$ trong dãy mà $i<j-2$ thì tồn tại $a_h;a_k$ sao cho $(a_h;a_k)\vdots[a_i;a_j]$. Tìm GTLN của số các giá trị khác nhau trong dãy.

Xét $\left\{\begin{matrix}
(a_2;a_3)\vdots[a_1;a_4]\Rightarrow a_3\geq(a_2;a_3)\geq[a_1;a_4]\geq a_4
\\
(a_4;a_5)\vdots[a_3;a_6]\Rightarrow a_4\geq(a_4;a_5)\geq[a_3;a_6]\geq a_3
\end{matrix}\right.$
$\Rightarrow a_3=a_4.$
Tương tự, ta được $a_3=a_4=a_5=...=a_{n-2}.$
Mặt khác $\left\{\begin{matrix}
(a_3;a_4)\vdots[a_2;a_5]\Rightarrow a_4\geq(a_3;a_4)\geq[a_2;a_5]\geq a_2
\\
(a_2;a_3)\vdots[a_1;a_4]\Rightarrow a_2\geq(a_2;a_3)\geq[a_1;a_4]\geq a_4
\end{matrix}\right.$
$\Rightarrow a_2=a_4.$ Tương tự $a_{n-1}=a_{n-3}\Rightarrow a_2=a_3=...=a_{n-1}.$ Suy ra số các giá trị khác nhau $\leq3.$
Ta sẽ chỉ ra tập có 3 giá trị khác nhau. Thật vậy, xét $(a_1;a_2;...;a_{n-1};a_n)=(45;180;...;180;15)$ thỏa mãn điều kiện trên.

Mở rộng 1: Ta sẽ mở rộng lên $n$ số $a_1;a_2;...;a_n.$ Cách chứng minh cũng tương tự như với 2012 số.
Ta kí hiệu $[a;b]$ là bội chung nhỏ nhất của $a$ và $b.$
Theo đề bài: $a_2\vdots [a_1;a_3]\Rightarrow a_2\geq[a_1;a_3]\geq a_3.(1)$
Tương tự, $a_3\vdots [a_2;a_4]\Rightarrow a_3\geq a_2.(2)$
Từ $(1),(2)$ ta suy ra $a_2=a_3.$
Tương tự, ta được $a_3=a_4=a_5=...=a_{n-2}=a_{n-1}\Rightarrow$ số các giá trị khác nhau $\leq3.$
Ta sẽ chỉ ra 1 bộ có 3 giá trị khác nhau. Thật vậy, xét $(a_1;a_2;...;a_{n-1};a_{n})=(12;36;...;36;18)$ thỏa mãn đề bài.

Mở rộng 4: Thử đảo ngược mở rộng 3 chút ít, ta thu được 1 bài toán mới:

Cho dãy $n$ số nguyên dương $a_1;a_2;...;a_n$ thỏa mãn tính chất sau: với mọi phần tử $a_i;a_j$ trong dãy mà $i<j-2$ thì tồn tại $a_h;a_k$ sao cho $[a_h;a_k]|(a_i;a_j)$. Tìm GTLN của số các giá trị khác nhau trong dãy.

Xét $[a_2;a_3] | (a_1;a_4)\Rightarrow a_3\leq [a_2;a_3]\leq (a_1;a_4)\leq a_4$
$[a_4;a_5] | (a_3;a_6)\Rightarrow a_4\leq [a_4;a_5]\leq (a_3;a_6)\leq a_3$
$\Rightarrow a_3=a_4.$
Tương tự, ta được $a_3=a_4=a_5=...=a_{n-2}.$
Mặt khác $[a_3;a_4]|(a_2;a_5)\Rightarrow a_4\leq[a_3;a_4]\leq(a_2;a_5)\leq a_2$
$[a_2;a_3]|(a_1;a_4)\Rightarrow a_2\leq[a_2;a_3]\leq(a_1;a_4)\leq a_4$
$\Rightarrow a_2=a_4.$ Tương tự $a_{n-1}=a_{n-3}\Rightarrow a_2=a_3=...=a_{n-1}.$ Suy ra số các giá trị khác nhau $\leq3.$
Ta sẽ chỉ ra tập có 3 giá trị khác nhau. Thật vậy, xét $(a_1;a_2;...;a_{n-1};a_n)=(128;180;...;180;15)$ thỏa mãn điều kiện trên.

Mở rộng 2: Lần này ta sẽ thử thay yếu tố BCNN thành ƯCLN và được bài toán sau:
Cho dãy $n$ số nguyên dương $a_1;a_2;...;a_n$ thỏa mãn tính chất sau: với mọi phần tử $a_i;a_j$ trong dãy mà $i<j-1$ thì tồn tại $a_k$ với $i<k<j$ sao cho $a_k|ƯCLN(a_i;a_j)$. Tìm GTLN của số các giá trị khác nhau có trong dãy.

Kí hiệu (a;b) là ƯCLN của a và b.
Ta có: $\left\{\begin{matrix}
a_2|(a_1;a_3)\Rightarrow a_2\leq(a_1;a_3)\leq a_3\\
a_3|(a_2;a_4)\Rightarrow a_3\leq(a_2;a_4)\leq a_2
\end{matrix}\right.$
$\Rightarrow a_2=a_3.$
Tương tự, ta thu được $a_2=a_3=...=a_{n-2}=a_{n-1}\Rightarrow$ số các giá trị khác nhau $\leq3.$
Nhận thấy $(a_1;a_2;...;a_{n-1};a_n)=(60;15;...;15;30)$ có 3 giá trị khác nhau$\Rightarrow$ GTLN của số các giá trị khác nhau là 3.
P/S: hôm nay viết kiểu gì thế nhỉ >.<"

Ta kí hiệu $[a;b]$ là bội chung nhỏ nhất của $a$ và $b.$
Theo đề bài: $a_2\vdots [a_1;a_3]\Rightarrow a_2\geq[a_1;a_3]\geq a_3.(1)$
Tương tự, $a_3\vdots [a_2;a_4]\Rightarrow a_3\geq a_2.(2)$
Từ $(1),(2)$ ta suy ra $a_2=a_3.$
Tương tự, ta được $a_3=a_4=a_5=...=a_{2010}=a_{2011}\Rightarrow$ số các giá trị khác nhau $\leq3.$
Ta sẽ chỉ ra 1 bộ có 3 giá trị khác nhau. Thật vậy, xét $(a_1;a_2;...;a_{2011};a_{2012})=(12;36;...;36;18)$ thỏa mãn đề bài.

D-B=22h
E=10
F=4*10=40
S=96

Hic, lời giải trước ko có latex.
$36(a^2+11a+30)(a^2+11a+31)=(a^2+11a+12)(a^2+9a+20)(a^2+13a+42)$
$\Leftrightarrow 36(a+5)(a+6)(a^2+11a+31)=(a+4)(a+5)(a+6)(a+7)(a^2+11a+12)$
$\Leftrightarrow (a+5)(a+6)[(a+4)(a+7)(a^2+11a+12)-36(a^2+11a+31)]=0$
$\Leftrightarrow (a+5)(a+6)(a^4+22a^3+125a^2+44a-780)=0$
$\Leftrightarrow (a+5)^2(a+6)^2(a+13)(a-2)=0$
$\Leftrightarrow a$ thuộc tập hợp {-13;-6;-5;2}.
Vậy a thuộc tập hợp {-13;-6;-5;2}.
Mong BTC xóa bài kia của em đi.

D-B=1.1h
E=10
F=0
S=76.9

Đề mang đúng thương hiệu của bạn bong hoa cuc trang.
$(x-7)^1-(x-7)^11=0$
$\Leftrightarrow (x-7)[1-(x-7)^10]=0$
$\Leftrightarrow x=7$ hoặc $(x-7)^10=1$
$\Leftrightarrow x=7$ hoặc $x=8$ hoặc $x=6$.
Vậy $x \in {6;7;8}$
Sorry BTC em ko biết viết kí hiệu hoặc.

D-B=6.8h
E=10
F=1 * 10=10
S=81.2

Mở rộng 1: Giải pt: $(ax+b)^m-(ax+b)^n=0 (1)$ với $m,n\in N*; m\leq n.$
$(1)\Leftrightarrow (ax+b)^m[1-(ax+b)^{m-n}]=0$
$\Leftrightarrow ax+b=0 (2)$ hoặc $(ax+b)^{m-n}=1 (3)$.
Xét $(2):$
$TH1: a=0; b=0\Rightarrow$ vô số nghiệm.
$TH2: a=0; b\neq 0\Rightarrow$ vô nghiệm.
$TH3: a\neq 0\Rightarrow 1$ nghiệm duy nhất $x=-\frac{b}{a}$
Xét $(3):$
$TH1:m-n$ là số chẵn: $(3)\Leftrightarrow ax+(b-1)=0 (*)$ hoặc $ax+(b+1)=0 (**)$.
$(*):$
$TH1: a=0; b=1\Rightarrow$ vô số nghiệm.
$TH2: a=0; b\neq 1\Rightarrow$ vô nghiệm.
$TH3: a\neq 1\Rightarrow 1$ nghiệm duy nhất $x=\frac{1-b}{a}$
$(**):$
$TH1: a=0; b=-1\Rightarrow$ vô số nghiệm.
$TH2: a=0; b\neq -1\Rightarrow$ vô nghiệm.
$TH3: a\neq 0\Rightarrow 1$ nghiệm duy nhất $x=-\frac{b+1}{a}$

Làm sao bạn biết chỉ có $0^1=0^{11}; 1^1=1^{11}; (-1)^1=(-1)^{11}$ mà các số khác lại không được?

Trước tiên mình xin lỗi vì cung cấp đáp án muộn . Do bài vở ở trên lớp còn chưa xong nên như các bạn thấy mình onl hơi muộn . Thôi , vào chuyện chính nào .

Có khá nhiều cách để làm bài này . Đây là cách lớp 6-7 :

Giải :

$(x-7)^1-(x-7)^{11}=0\Leftrightarrow (x-7)^1=(x-7)^{11}$

Nhận thấy $11>1$ . Mà $11$ và $1$ đều là số lẻ nên $(x-7)$ sẽ nhận các giá trị :

$+)TH1:$ $x-7=1$ (vì $1^1=1^{11}$)
$\to x=8$
$+)TH2:$ $x-7=0$ (vì $0^1=0^{11}$)
$\to x=7$
$+)TH3:$ $x-7=-1$ (vì $(-1)^1=(-1)^{11}$)
$\to x=6$

Vậy : $ x\epsilon \left \{ 8;7;6 \right \}$

p/s : Vậy các bạn có thấy đáp án bài này có bất ngờ không ? 3 số tự nhiên liên tiếp .

Cách giải mang nặng tính "mò".

Nhận xét: $MB^2-MC^2=2MA^2\Rightarrow MB^2=MC^2+2MA^2$.
TH1: $M$ nằm trong $\triangle{ABC}$:

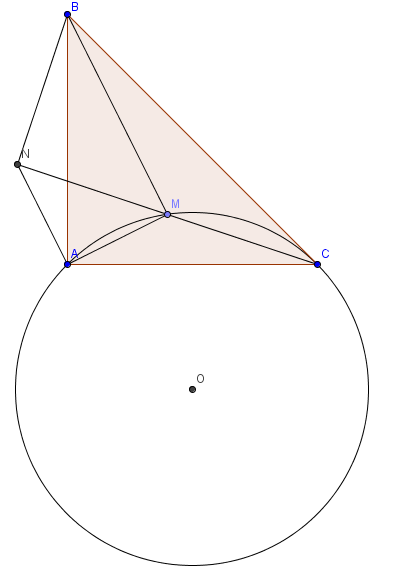
Dựng $\triangle{MAN}$ vuông cân tại A như trên hình vẽ.
Theo định lí Pytago, ta có: $2MA^2=MN^2$.
$\triangle{AMC}=\triangle{ANB}(c.g.c)\Rightarrow MC=NB.$
Xét $\triangle{MNB}$ có $MN^2+NB^2=2MA^2+MC^2=MB^2\Rightarrow \triangle{MNB}$ vuông tại $N\Rightarrow \angle{MNB}=90\Rightarrow \angle{ANB}=\angle{AMC}=135.$
$\Rightarrow M$ sẽ chạy trên cung nhỏ $AC$ của $(O;OA)$ với $\angle{AOC}=360-135.2=90$.
TH2: $M$ nằm ngoài $\triangle{ABC}$:

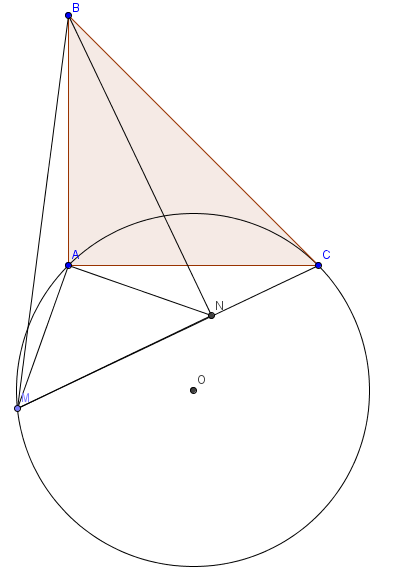
Dựng $\triangle{MAN}$ vuông cân tại A như trên hình vẽ.
Theo định lí Pytago, ta có: $2MA^2=MN^2$.
$\triangle{AMC}=\triangle{ANB}(c.g.c)\Rightarrow MC=NB.$
Xét $\triangle{MNB}$ có $MN^2+NB^2=2MA^2+MC^2=MB^2\Rightarrow \triangle{MNB}$ vuông tại $N\Rightarrow \angle{MNB}=90\Rightarrow \angle{ANB}=\angle{AMC}=45.$
$\Rightarrow M$ sẽ chạy trên cung lớn $AC$ của $(O;OA)$ với $\angle{AOC}=45.2=90$.
Vậy $M$ sẽ chạy trên đường tròn $(O:OA)$.

Em làm cách suy ra, sao không có phần đảo?
D-B=17.5h
E=7đ
F=0
S=51.5

Ta có: $x^4+y^4+z^4+104x=1984 (1)$
$\Rightarrow 1\leq x^4,y^4,z^4<1984\Rightarrow 1\leq x,y,z\leq6.$
Mặt khác, ta nhận thấy $(1984-104x)\vdots4$ mà $x^4,y^4,z^4$ chia cho $4$ chỉ dư $0$ hoặc $1\Rightarrow x^4,y^4,z^4\vdots4\Rightarrow x,y,z\vdots2\Rightarrow x,y,z \in \left{ {2;4;6} \right\}.$ X
Vì $A$ là số tự nhiên$\Rightarrow 20^x+11^y\geq 1969^z\Rightarrow z\leq 2\Rightarrow z=2.$ Mặt khác $x=6$.(nếu $x<6$ thì $20^x+11^y\leq 20^4+11^6<1969^2$, loại)
Xét các trường hợp:
$*y=6\Rightarrow x^4+y^4+z^4+104x=3232>1984.$(loại)
$*y=4\Rightarrow x^4+y^4+z^4+104x=2192>1984.$(loại)
$*y=2\Rightarrow x^4+y^4+z^4+104x=1952<1984.$(loại)
Vậy $A$ không thể viết dưới dạng $a+a^2$ với $a$ là số tự nhiên.

Từ chỗ X trở về sau, lời giải không đúng.
D-B=21.6h
E=3
F=0
S=35.4

Bài 2:
Đặt $\sqrt{x}=a; \sqrt{y}=b\Rightarrow a,b>0.$
Viết lại đề bài: $\frac{a^8+b^8}{(a^2+b^2)^4}+\frac{ab}{a^2+b^2}\geq\frac{5}{8}$
$\Leftrightarrow \frac{a^8+b^8+ab(a^2+b^2)^3}{(a^2+b^2)^4}\geq\frac{5}{8}$
$\Leftrightarrow 8[a^8+b^8+ab(a^2+b^2)^3]\geq5(a^2+b^2)^4$
$\Leftrightarrow 8a^8+8b^8+8a^7b+24a^5b^3+24a^3b^5+8ab^7-5a^8-20a^6b^2-30a^4b^4-20a^2b^6-5b^8\geq0$
$\Leftrightarrow (a-b)^2(3a^2+2ab+3b^2)(a^4+4a^3b-2a^2b^2+4ab^3+b^4)\geq0$
BĐT cuối đúng vì:$\left\{\begin{matrix}
(a-b)^2\geq0\\
3a^2+2ab+3b^2>0\\
a^4+4a^3b-2a^2b^2+4ab^3+b^4=(a^2-b^2)+4ab(a^2+b^2)>0
\end{matrix}\right.$
Vậy ta có đpcm.

Sorry bài kia em viết thiếu:
Dấu $"="$ xảy ra$\Leftrightarrow a=b\Leftrightarrow x=y.$
Mong BTC ghép 2 bài vào nhau.

Từ đầu thì $a,b \ge 0$ và $a+b \neq 0$. Xét thiếu TH $a=0$ hoặc $b=0$.
D-B=9.5h
E=8.3
F=0
S=63.4

Ta có hệ pt sau: $\left\{\begin{matrix}
ax+by+cz=xyz(1)\\
\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}=x+y+z(2)
\end{matrix}\right.$ với $a,b,c,x,y,z>0.$
Chia 2 vế của $(1)$ cho $xyz>0$ ta được $\frac{a}{yz}+\frac{b}{xz}+\frac{c}{xy}=1$
$\Rightarrow \frac{a}{yz}+\frac{b}{zx}<1$ (vì $\frac{c}{xy}>0$)
$\Leftrightarrow z>\frac{a}{y}+\frac{b}{x}.$
Tương tự, $x>\frac{b}{z}+\frac{c}{y}; y>\frac{a}{z}+\frac{c}{x}.$
Khi đó $2(x+y+z)>\frac{b}{z}+\frac{c}{y}+\frac{a}{z}+\frac{c}{x}+\frac{a}{y}+\frac{b}{x}+x+y+z$
$=(\frac{a+b}{z}+z)+(\frac{b+c}{x}+x)+(\frac{c+a}{y}+y)$
$\geq 2(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a})$ (AM-GM 2 số)
$\Leftrightarrow \sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}<x+y+z (3)$
Từ $(2),(3)\Rightarrow$ pt vô nghiệm.

Bài giải chính xác. Chuẩn ko cần chỉnh
D - B = 30h
E = 10
F = 0
S = 48

Bài làm của daovuquang:

Lấy K đối xứng với E qua AB, L đối xứng với E qua AC, J đối xứng với F qua BC.
Theo gt, $\widehat{ABE}=\widehat{CBF}\Rightarrow \widehat{ABF}=\widehat{CBE}(1).$
Từ cách vẽ trên, ta được $\widehat{EBA}=\widehat{KBA}\Rightarrow\widehat{CBF}=\widehat{KBA}.$ Mặt khác $\widehat{FBC}=\widehat{JBC}\Rightarrow \widehat{KBA}=\widehat{JBC}(2).$
Kết hợp $(1),(2)\Rightarrow \widehat{KBF}=\widehat{EBJ}.$ Lại có $KB=EB, FB=JB$( theo cách vẽ)
$\Rightarrow \triangle{KBF}=\triangle{EBJ}(c.g.c)\Rightarrow KF=EJ.$
Mặt khác, xét $\triangle{AKF}$ và $\triangle{ALF}$ có:$\left\{\begin{matrix}
AF chung\\
AK=AL(=AE)\\
\widehat{KAF}=\widehat{LAF}(=\widehat{BAC})
\end{matrix}\right.$
$\Rightarrow \triangle{AKF}=\triangle{ALF}(c.g.c)\Rightarrow KF=LF\Rightarrow EJ=LF.$
Mà theo cách vẽ, $EC=LC và JC=FC\Rightarrow \triangle{EJC}=\triangle{LFC}(c.c.c)\Rightarrow \widehat{ECJ}=\widehat{LCF}\Rightarrow \widehat{BCJ}+\widehat{ECB}+\widehat{FCE}=\widehat{LAC}+\widehat{ACF}+\widehat{FCE}\Rightarrow \widehat{FCB}=\widehat{ACE}\Rightarrow Q.E.D.$

D-B=15.8h
E=10
F=0
S=62.2

Bổ sung cho lời giải, đó chỉ là trường hợp F nằm giữa A và E. Còn trường hợp E nằm giữa A và F thì cũng tương tự.