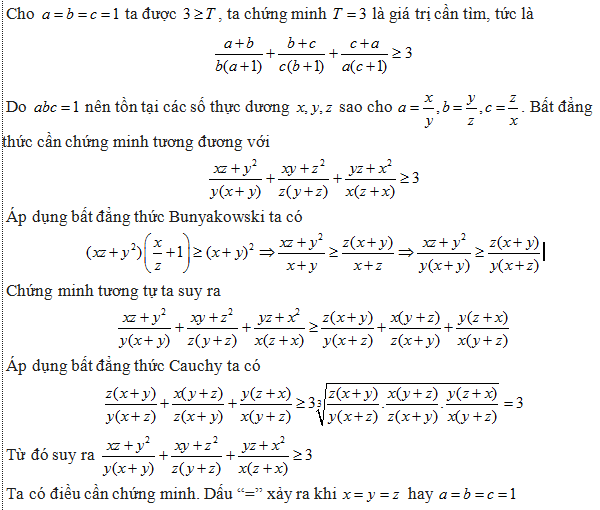Bài 18 (Macedonia National Olympiad). Cho $n \;(n \geqslant 3)$ số thực dương $a_1,\,a_2,\,\ldots,a_n$ thỏa mãn điều kiện

$$\frac{1}{1+a_1^4} + \frac{1}{1+a_2^4} + \cdots + \frac{1}{1+a_n^4} = 1.$$

Chứng minh rằng $$a_1a_2 \cdots a_n \ge (n-1)^{\frac n4}.$$
 

 Bài này quen thuộc

 Áp dụng bất đẳng thức AM-GM ta có $\dfrac{a_1^4}{1+a_1^4}=\dfrac{1}{1+a_2^4}+\dfrac{1}{1+a_3^4}+...+\dfrac{1}{a_n^4}\geq (n-1)\sqrt[n-1]{\dfrac{1}{(1+a_2^4)(1+a_3^4)...(1+a_n^4)}}$

 Tương tự thì $\begin{matrix}\dfrac{a_2^4}{1+a_2^4}\geq (n-1)\sqrt[n-1]{\dfrac{1}{(1+a_1^4)(1+a_3^4)...(1+a_n^4)}}\\ \dfrac{a_3^4}{1+a_3^4}\geq (n-1)\sqrt[n-1]{\dfrac{1}{(1+a_1^4)(1+a_2^4)...(1+a_n^4)}} \\... \\ \dfrac{a_n^4}{1+a_n^4}\geq (n-1)\sqrt[n-1]{\dfrac{1}{(1+a_1^4)(1+a_2^4)...(1+a_{n-1}^4)}}\end{matrix}$

 Nhân các bất đẳng thức trên lại ta được $\prod _{i=1}^n \dfrac{a_i^4}{1+a_i^4}\geq (n-1)^n.\dfrac{1}{\prod \limits _{i=1}^n (1+a_i^4)}$

 Thu gọn và lấy căn 2 vế ta có điều cần chứng minh

Bài 34 (Serbia Junior TST). Cho $a,b,c$ là ba số thực dương. Chứng minh rằng $$\frac{2a}{\sqrt{3a+b}}+\frac{2b}{\sqrt{3b+c}}+\frac{2c}{\sqrt{3c+a}}\leq \sqrt{3(a+b+c)}.$$
 

 Áp dụng bất đẳng thức Cauchy-Schwarz ta có $\sum \dfrac{2a}{\sqrt{3a+b}}\leq 2\sqrt{(a+b+c)\sum \dfrac{a}{3a+b}}$

 Nên ta chỉ cần chứng minh $\sum \dfrac{a}{3a+b}\leq \dfrac{3}{4}\Leftrightarrow \sum \dfrac{b}{3a+b}\geq \dfrac{3}{4}$

 Áp dụng bất đẳng thức Cauchy-Schwarz ta có $\sum \dfrac{b}{3a+b}=\sum \dfrac{b^2}{3ab+b^2}\geq \dfrac{(a+b+c)^2}{(a+b+c)^2+ab+bc+ca}\geq \dfrac{3}{4}$

 Dấu "=" xảy ra khi $a=b=c$

Bài 39 (Mediterranean MO). Cho ba số thực dương $a,b,c$ thỏa mãn $a+b+c=3.$ Chứng minh rằng
\[\sqrt{\frac{b}{a^2+3}}+\sqrt{\frac{c}{b^2+3}}+\sqrt{\frac{a}{c^2+3}} \leqslant \frac32\sqrt[4]{\frac{1}{abc}}.\]
 

 Vế phải của bất đẳng thức thực ra là $\dfrac{1}{2}.\dfrac{3}{\sqrt[4]{abc}}=\dfrac{a+b+c}{2\sqrt[4]{abc}}$

 Áp dụng bất đẳng thức AM-GM thì $a^2+3\geq 4\sqrt{a}$ nên $VT\leq \sum \dfrac{\sqrt{b}}{2\sqrt[4]{a}}$

 Đặt $\sqrt[4]{a}=x,\cdots $ thì ta chỉ cần chứng minh $\sum \dfrac{y^2}{x}\leq \dfrac{x^4+y^4+z^4}{xyz}\Leftrightarrow x^3y+y^3z+z^3x\leq x^4+y^4+z^4$

 Bất đẳng thức trên chứng minh khá dễ bằng AM-GM

 Bài 2. Ta chú ý đến một phân tích quen thuộc là $(x+y)^2=(x-y)^2+4xy$

 Bây giờ đặt $\sum _{j=1}^na_jb_j=S$ và $a_{i}b_{i}=S_i$ thì ta cần chứng minh $\sum_{i=1}^n \dfrac{(a_{i+1}+b_{i+1})^2}{n(a_i-b_i)^2+4(n-1)S} \geq \dfrac{1}{n-1}$

 Hay $\sum_{i=1}^n \dfrac{(a_{i+1}-b_{i+1})^2+4S_{i+1}}{n(a_i-b_i)^2+4(n-1)S} \geq \dfrac{1}{n-1}$

 Không mất tính tổng quát giả sử $(a_1-b_1)^2\leq \min \left \{(a_2-b_2)^2,(a_3-b_3)^2,...,(a_n-b_n)^2\right \}$ thì ta có

 $\sum_{i=1}^n \dfrac{(a_{i+1}-b_{i+1})^2+4S_{i+1}}{n(a_i-b_i)^2+4(n-1)S} \geq \dfrac{\sum \limits_{i=1}^n (a_{i}-b_{i})^2+4\sum \limits_{k=1}^nS_{k}}{n(a_1-b_1)^2+4(n-1)S}=\dfrac{\sum \limits_{i=1}^n (a_{i}-b_{i})^2+4S}{n(a_1-b_1)^2+4(n-1)S}$

 Nên ta chỉ cần chứng minh $\dfrac{\sum \limits_{i=1}^n (a_{i}-b_{i})^2+4S}{n(a_1-b_1)^2+4(n-1)S}\geq \dfrac{1}{n-1}\Leftrightarrow \sum_{i=1}^n (a_{i}-b_{i})^2\geq \dfrac{n}{n-1}(a_1-b_1)^2\Leftrightarrow \sum_{i=2}^n (a_{i}-b_{i})^2\geq \dfrac{1}{n-1}\geq (a_1-b_1)^2$

 Áp dụng bất đẳng thức Cauchy-Schwarz ta có $\sum_{i=2}^n (a_{i}-b_{i})^2\geq \dfrac{1}{n-1}\left (\sum_{j=2}^n a_j-\sum_{k=2}^n b_k \right )^2$

 Mặt khác $\sum_{i=1}^n (a_i-b_i)=0$ nên $\left (\sum_{j=2}^n a_j-\sum_{k=2}^n b_k \right )^2=(a_1-b_1)^2$

 Từ đó ta có điều cần chứng minh ~.~ Mỏi tay

 Bài 11. Không giảm tính tổng quát giả sử $a>b>c$ ( hiển nhiên $a,\ b,\ c$ đôi một không đồng thời bằng nhau )

 Khi đó ta có $1=(a-b)(b-c)(a-c)\leq \dfrac{1}{4}(a-c)^3\Rightarrow a-c\geq \sqrt[3]{4}$

 Lại có $|a|+|b|+|c|\geq |a-c|+|b|\geq a-c\geq \sqrt[3]{4}$ nên ta có giá trị nhỏ nhất

 Dấu "=" xảy ra khi và chỉ khi $b=0;a=-c=\dfrac{1}{\sqrt[3]{2}}$

 Mà mình thấy có mấy câu hơi dở đi nhỉ 

Bài 52 (Taiwan TST). Tìm hằng số $k$ nhỏ nhất để bất đẳng thức

\[\frac{x^2y^2}{1-z}+\frac{y^2z^2}{1-x}+\frac{z^2x^2}{1-y}\leq k-3xyz,\]

luôn đúng với mọi số thực dương $x,y,z$ thỏa mãn điều kiện $x+y+z=1.$

 Áp dụng AM-GM ta có $\sum \dfrac{x^2y^2}{1-z}=\sum \dfrac{x^2y^2}{x+y}\leq \sum \dfrac{xy(x+y)}{4}$

 Nên ta sẽ có $\sum \dfrac{x^2y^2}{1-z}+3xyz\leq \dfrac{1}{4}\left(\sum xy(x+y)+12xyz\right)=\dfrac{1}{4}\left(xy+yz+zx+9xyz\right)\leq \dfrac{1}{6}$

 Hơn nữa tại $k=\dfrac{1}{6}$ thì bất đẳng thức xảy ra dấu "=" tại $x=y=z=1/3$ nên $k_{\min}=\dfrac{1}{6}$

 Câu 3 em nghĩ chỉ cần làm như sau

 Đặt $n=mq+r$ với $0<r<m$ thì khi xét trong $\text{mod 2016}$ ta có $2016^m\equiv -1\Rightarrow 2016^{mq+r}\equiv (-1)^q.2016^r\Rightarrow 2016^r.(-1)^q+1\vdots 2016^m+1$ 

 Mà ta có $|2016^r.(-1)^q+1|\leq |2016^r+1|\leq 2016^m+1$ nên điều trên xảy ra khi $q$ lẻ và $r=0$

 Vậy ta có điều cần chứng minh

 Câu bất đẳng thức thì dùng Cauchy Schwarz $\sum \dfrac{b}{a^2}.\sum \dfrac{1}{ab}.(1+1+1)\geq \left (\sum \dfrac{1}{a}\right )^3$ sau đó biến đổi tương đương cũng ra

Bài hình ngày 1:

a, Bằng biến đổi góc ta có $DKG=FKE$ do đó $GKE=DKF=DPF$. Bằng phương tích suy ra $GDFE$ nội tiếp. Ta chứng minh được $(P,D,G)$ và $(P,F,E)$ thẳng hàng (bằng cộng góc). Từ các điều kiện trên ra có DPCM

Ai có lời giải câu b chưa vậy. Câu a khá đơn giản nhưng câu b làm tốn thời gian quá!!  

 Bạn ghi rõ đoạn chứng minh thằng hàng được không, mình cũng cộng góc mà không ra.

 P/s: Ai giải câu 5 đi

Câu 4.

 a) Ta có $\angle PKB=\angle 180^\circ -\angle MKB=180^\circ -\angle MAB=\angle BAN=\angle BLN=180^\circ -\angle BLP$ nên tứ giác $PKBL$ nội tiếp

 b) Ta có $\angle BKO_2=\angle BO_1O_2=\dfrac{1}{2}\angle BOA=\angle BKA$ nên $K,A,O_2$ thằng hàng, tương tự cho $L,A,O_1$

 Do đó mà $\angle KBA=\dfrac{1}{2}\angle KO_1A=\dfrac{180^\circ -\angle KAO_1}{2} =\dfrac{180^\circ -\angle LAO_2}{2}=\dfrac{1}{2}\angle LO_2A=\angle LBA$

 Nên $BA$ là phân giác $\angle KBL$, do đó $A$ cách đều $BK$ và $BL$

 c) Ta có $\angle PMN=\angle KBA=\angle LBA=\angle PNM$ nên tam giác $PMN$ cân tại $P$

 Nếu $P\in AB$ thì $PK.PM=PA.PB=PL.PN$ nên $PK=PL$

 Nếu $PK=PL$ thì $PK.PM=PL.PN$ nên nếu gọi $A'$ và $A''$ là giao $PB$ với $(O_1)$ và $(O_2)$ thì $PK.PM=PA'.PB=PL.PN=PA''.PB$

 Do đó $A'\equiv A''\equiv A$, và đó đó $P\in AB$

Câu 4. 

a. Ta có $\angle NCM=\angle CAE=\angle NAM$ nên tứ giác đó nội tiếp

b. Có một kết quả quen thuộc là $\angle CAO+\angle ABC=90^\circ$, mà $\angle ABC=\angle AKD$ nên suy ra điều cần chứng minh

c. Sử dụng Thales do $EF\parallel CD$ nên $\dfrac{NF}{CN}=\dfrac{EF}{CD}\Rightarrow \dfrac{CF}{CN}=1-\dfrac{CF}{CD}$

 Chuyến vế ta có điều cần chứng minh

 Cách của mình có lẽ gọn hơn xíu, như sau

 Áp dụng AM-GM ta có $3\sqrt[3]{z^2x^2}+1\leq xz+x+z+1=(x+1)(z+1)$ và $(2x+3y+z)^3=(x+2y+3)^3=(x+1+y+1+y+1)^3\geq 27(x+1)(y+1)^2$

 Áp dụng bất đẳng thức Cauchy-Schwarz ta có $P\geq 27\left [\dfrac{(y+1)^2}{z+1}+\dfrac{(z+1)^2}{x+1}+\dfrac{(x+1)^2}{y+1}\right ]\geq 27(x+y+z+3)=162$

 Dấu "=" xảy ra khi $x=y=z=1$

Tìm $f:R\rightarrow R$ thỏa mãn:

$f(x+y)+f(x)f(y)=f(xy)+f(x)+f(y)$ (1)

Với mọi $x,y$ thực

 Thay $y:=0$ vào (1) ta được $f(0)(f(x)-2)=0$, cho tiếp $x:=0$ suy ra $f(0)=0$ hoặc $f(0)=2$

 Với $f(0)=2$ thì suy ra $f(x)\equiv 2$

 Với $f(0)=0$, thay $x,y$ trong (1) bởi 2 suy ra $f(2)(f(2)-2)=0$

  - Nếu $f(2)=0$, thay $y=x=1$ vào (1) suy ra $f(1)=0$ hoặc $f(1)=3$

    Với $f(1)=3$, thay $y$ lần lượt bởi $1$ và $2$ vào (1) suy ra $f(x+1)+f(x)=3$ và $f(x+2)=f(2x)+f(x)$, suy ra $f\equiv 0$, vô lí

    Với $f(1)=0$, thay $y:=1$ vào (1) suy ra $f(x+1)=2f(x)$, thay tiếp $x:=x+1$ vào (1) ta có

     $f(x+y+1)+f(x+1)f(y)=f(xy+y)+f(x+1)+f(y)\Leftrightarrow f(xy+y)=2f(xy)+f(y)$, hay $f(x+y)=2f(x)+f(y)=f(x)+2f(y)$, suy ra $f$ hằng hay $f\equiv 0$

  - Nếu $f(2)=2$, thay $x,y$ trong (1) bởi 1 suy ra $f(1)=1$ hoặc $f(1)=2$ 

    Với $f(1)=2$, thay $y:=1$ vào (1) suy ra $f\equiv 2$, vô lí 

    Với $f(1)=1$, thay $y:=1$ vào (1) suy ra $f(x+1)=f(x)+1$ 

    Lại thay $x:=x+1$ vào (1) và biến đổi suy ra $f(xy+y)=f(xy)+f(y)$ hay $f(x+y)=f(x)+f(y)$, suy ra $f(xy)=f(x)f(y)$, với mọi $x,y\in \mathbb{R}$

    Từ đây suy ra $f(x)=x$ 

 Vậy có 3 nghiệm hàm thỏa mãn $f(x)\equiv 0, f(x)\equiv 2, f(x)=x,\forall x\in \mathbb{R}$

Bài này là TST chứ bạn 

Bài T9/465 giải như sau có vẻ gọn gàng hơn

P/s: Bài T12 mình giải không hay nên cũng không muốn post

 Một cách nữa cũng khá gọn

 Còn đây là lời giải của mình cho bài T10

Bài Toán:

 

Cho tập $ A= \{ 1; 2 ; 3; ...; 8 \}$ hỏi có thể có bao nhiêu số có 6 chữ số phân biệt được xếp theo trình tự từ bé đến lớn sao cho 6 chữ số này được chọn từ tập $A$ đã cho ?

 Em nghĩ chỉ việc chọn 6 số bất kì trong 8 số trên, còn việc sắp xếp thứ tự thì sau khi chọn do 6 số phân biệt nên mỗi cách chọn 6 số sẽ cho ra duy nhất một số và không lặp. 

Lời giải cho bài toán tổng quát

 Kedlaya.pdf   224.76K   289 Số lần tải

Cho các số thực dương a,b,c thỏa mãn abc=1

Chứng minh rằng $\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+3\geq 2(a+b+c)$

 Áp dụng bất đẳng thức Schur bậc 3 và bất đẳng thức AM-GM ta có

$\begin{eqnarray*}\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+3 &=& a^2b^2+b^2c^2+c^2a^2+3\sqrt[3]{a^4b^4c^4}\\ &\geq & \sum \sqrt[3]{a^2b^2.b^2c^2}(\sqrt[3]{a^2b^2}+\sqrt[3]{b^2c^2})\\ &=&\sum \sqrt[3]{b^4}(\sqrt[3]{a^2}+\sqrt[3]{c^2})\\ &\geq &2\sum \sqrt[3]{b^4ac}=2\sum a  \end{eqnarray*}$

Cách dưới thì giống của mình rồi,còn cách làm Chebyshev thì tốt lắm

 Cách của mình :

 Ta có bất đẳng thức tương đương $\sum \left (\dfrac{4}{3}-\dfrac{1}{1-ab}\right )\geq \dfrac{5}{8}\Leftrightarrow \sum \dfrac{(1-4ab)^2}{(1-4ab)(1-ab)}\geq \dfrac{15}{8}$

 Do $1=(a+b+c)^2>(a+b)^2\geq 4ab$ nên áp dụng bất đẳng thức Cauchy-Schwarz ta có

 $\sum \dfrac{(1-4ab)^2}{(1-4ab)(1-ab)}\geq \dfrac{(3-4\sum ab)^2}{\sum (1-4ab)(1-ab)}=\dfrac{(3-4q)^2}{3-5q+4q^2-8r}\geq \dfrac{(3-4q)^2}{3-5q+4q^2-\dfrac{8(4q-1)}{9}}$

 Ta cần chứng minh $\dfrac{(3-4q)^2}{3-5q+4q^2-\dfrac{8(4q-1)}{9}}\geq \dfrac{15}{8}\Leftrightarrow (3q-1)(68q-41)\geq 0$

 Đúng do $q\leq \dfrac{1}{3}$

 -----------------

 Cái dạng này nhìn khá quen, không biết có lời giải bằng tiếp tuyến hoặc yếu tố không

Mình không biết tại sao lại có ý tưởng thêm bớt $\frac{4}{3$ ở khúc này ? Bạn có thể giải thích không ?

 Mình đưa bất đẳng thức về chứng minh tương đương $\sum \left (k-\dfrac{1}{1-ab}\right )\geq 3k-\dfrac{27}{8}\Leftrightarrow \sum \dfrac{k-1-kab}{1-ab}\geq 3k-\dfrac{27}{8}$

 Dạng này nhìn có vẻ quen, vì các bài toán tương tự để giải bằng yếu tố hay Cauchy-Schwarz đếu có thể đưa về như vậy, và mình thêm bớt để có thể sử dụng Cauchy-Schwarz. Ta sẽ cần tìn một đánh giá cho $ab$ sao cho bất đẳng thức $k-1>kab$ càng chặt càng tốt. Ta có một số đánh giá như sau :

 $ab\leq \dfrac{(a+b)^2}{4}\leq \dfrac{a^2+b^2}{2}\leq \dfrac{1}{2}$

 $3(ab+bc+ca)\leq (a+b+c)^2$, cho $c\rightarrow 0$ thì thành $1\geq 3ab$

 $1=(a+b+c)^2>(a+b)^2\geq 4ab$

 Tuy nhiên nếu để ý một tí thì ta nhận ra rằng đánh giá $(a+b)^2\geq 4ab$ chặt hơn $a^2+b^2\geq 2ab$, và tuy rằng nó chưa phải chặt nhất ( vì theo mình biết thì còn có cả cái mà "Làm mạnh bất đẳng thức Cauchy" nữa ), lúc đó không biết do vô tình hay sao nhưng mình nghĩ $ab<\dfrac{1}{4}$ có lẽ là vừa đủ. 

 Tiếp theo và việc chọn hằng số $k$ sao cho $\dfrac{k-1}{1}=\dfrac{k}{4}\Leftrightarrow k=\dfrac{4}{3}$, việc tiếp theo như bạn thấy

 Nhưng thực ra mình nghĩ lời giải của mình ở trên vẫn mang hơi hướng gì đó hơi may mắn một tí, thực ra trong quá trình biến đổi mình có sai và tưởng như $\dfrac{1}{4}$ vẫn là không đủ. Và nói thật, lúc đó mình định buông xuôi May dò lại được

Ai có lời giải thuần bằng C-S hay AM-GM thì post lên nhé

 

Xét phép đổi biến $p,q,r$,ta sẽ có $r\in \left ( 0;\frac{1}{27} \right ]; q \in \left ( 0;\frac{1}{3} \right ]$.Theo Schur thì $r\geqslant \frac{4q-1}{9}$

 

BĐT cần chứng minh tương đương với:

$\sum \frac{ab}{1-ab}\leqslant \frac{3}{8}\Leftrightarrow \sum \frac{1}{1-ab}\leqslant \frac{27}{8}\Leftrightarrow \frac{\sum (1-ab)(1-bc)}{(1-ab)(1-bc)(1-ca)}\leqslant \frac{27}{8}$

$\Leftrightarrow \frac{3-2q+r}{1-q+r-r^{2}}\leqslant \frac{27}{8}\Leftrightarrow f(r)=27r^{2}-19r+11q-3\leqslant 0$

 

Dễ thấy $f'(r)=54r-19<0,\forall r \in \left ( 0;\frac{1}{27} \right ]$ nên $f(r)\leqslant f\left ( \frac{4q-1}{9} \right )=\frac{(16q+5)(3q-1)}{9}\leqslant 0,\forall q \in \left ( 0;\frac{1}{3} \right ]$

 

Ta có đpcm.

 Có hai cách khác ở đây ạ http://diendantoanho...-xyleq-frac278/

theo BĐT trên thì ta sẽ đi chứng minh : 

$\sum \frac{a^4}{1+a^2b}\geq \sum \frac{a^3b}{1+ab^2}\Leftrightarrow \sum \frac{a^3(a-b)}{(1+a^2b)(1+ab^2)}\geq 0$

Ta có : $\frac{a^3(a-b)}{X}+\frac{b^3(b-c)}{Y}+\frac{c^3(c-a)}{Z}=\frac{(a-b)^2(a^2+ab+b^2)}{M}+\frac{(b^3-c^3)(a-c)}{N}\geq 0$

BĐT trên đúng nếu giả sử $a\geq b\geq c$

BĐT đc CM $☺$

Có chắc là giả sử được không? :V

Lâu rồi mới gặp lại mà nó làm khó t.

      Bài 1: Chứng minh rằng với mọi số thực $a,b,c$, ta có:

$2(1+abc)+\sqrt{2(1+a^2)(1+b^2)(1+c^2)} \geq (1+a)(1+b)(1+c)$

      Bài 2: Chứng minh rằng với mọi $a,b,c > 0$, ta có:

$\frac{a^4}{1+a^2b}+\frac{b^4}{1+b^2c}+\frac{c^4}{1+c^2a} \geq \frac{abc(a+b+c)}{1+abc}$

      Bài 3: Cho $a,b,c$ là các số thực dương thõa mãn $a^2+b^2+c^2=3$

                 Chứng minh rằng:

$\sqrt{\frac{a^2}{a^2+b+c}}+\sqrt{\frac{b^2}{b^2+c+a}}+\sqrt{\frac{c^2}{c^2+a+b}} \leq \sqrt{3}$

 Bài 2 làm như sau

 Áp dụng bất đẳng đẳng thức Cauchy-Schwarz:

 $\sum \dfrac{a^4}{1+a^2b}=\sum \dfrac{a^4bc}{bc+a^2b^2c}\geq \dfrac{abc\left(a\sqrt{a}+b\sqrt{b}+c\sqrt{c}\right)^2}{(1+abc)(ab+bc+ca)}$

 Nên ta chỉ cần chứng minh $\left(a\sqrt{a}+b\sqrt{b}+c\sqrt{c}\right)^2\geq (a+b+c)(ab+bc+ca)$

 Mà $ab+bc+ca\leq \dfrac{1}{3}(a+b+c)^2$

 Cho nên chỉ cần chỉ ra $3\left(a\sqrt{a}+b\sqrt{b}+c\sqrt{c}\right)^2\geq (a+b+c)^3$

 Lấy căn bậc 6 hai vế thì nó tương đương $\sqrt[3]{\dfrac{\sqrt{a}^3+\sqrt{b}^3+\sqrt{c}^3}{3}}\geq \sqrt{\dfrac{\sqrt{a}^2+\sqrt{b}^2+\sqrt{c}^2}{3}}$

 Đúng theo bất đẳng thức trung bình lũy thừa

 

 Chuỗi 1:

 Cho x, y và z là ba số thực dương.

 Hãy tìm giá trị nhỏ nhất của biểu thức:

 

$P=\frac{1}{x+\sqrt{xy}+\sqrt[3]{xyz}}-\frac{2}{\sqrt{x+y+z}}.$

 

 Áp dụng bất đẳng thức AM-GM ta có $x+\sqrt{xy}+\sqrt[3]{xyz}\leq x+\dfrac{x+4y}{4}+\dfrac{x+4y+16z}{12}=\dfrac{4}{3}(x+y+z)$

 Đặt $\sqrt{x+y+z}=t$ thì $P\geq \dfrac{3}{4t^2}-\dfrac{2}{t}\geq \dfrac{-4}{3}$

 Dấu "=" xảy ra khi $16z=4y=x=\dfrac{3}{7}$

 

 Chuỗi 2:

 Cho x, y và z là ba số thực không âm, thoả mãn:

$xy+yz+zx=1.$

 Hãy tìm giá trị nhỏ nhất của biểu thức:

$P=\frac{1}{x^{2}+y^{2}}+\frac{1}{y^{2}+z^{2}}+\frac{1}{z^{2}+x^{2}}+\frac{5}{2}(x+1)(y+1)(z+1).$

 

 Giả sử $c=\min \{a,b,c\}$, khi đó ta có $\sum \dfrac{1}{x^2+y^2}\geq \dfrac{10}{(x+y+z)^2}$

 Lại có $(x+1)(y+1)(z+1)=xyz+1+x+y+z+xy+yz+zx\geq x+y+z+2$

 Đặt $t=x+y+z$ với $t\in [0;\sqrt{3}]$ thì $P\geq \dfrac{10}{t^2}+\dfrac{5(t+2)}{2}\geq \dfrac{35}{2}$

 Dấu "=" xảy ra khi $a=b=1,c=0$ cùng các hoán vị

Cho dãy số $(u_{n})$ thoả mãn điều kiện: $u_{1}=\frac{\sqrt{6}-\sqrt{2}}{2},u_{n+1}=\sqrt{2+u_{n}}$ với mọi $n=1,2,...$. CMR: Dãy số $(u_{n})$ có giới hạn và tìm $lim2^{n}\sqrt{2-u_{n}}$

 Đặt $u_1=2\cos \dfrac{5\pi}{12}$ và sau đó quy nạp chứng minh được $u_n=2\cos \dfrac{5\pi}{3.2^{n+1}}$, rồi sử dụng giới hạn $\lim _{x\to 0} \dfrac{\sin x}{x}=1$ là xong

 T8-463.doc   135K   218 Số lần tải