Anh Phudinhgioihan cũng đi thi ạ? Làm được bao nhiêu phần trăm vậy anh

Kết quả toán 10.pdf

Kết quả toán 11.pdf

Lớp 10 : 10 điểm đc HCV, 5 điểm được HCĐ @@~

Chấm ảo lắm chú, chặt chém không tha đâu =))

Cho tam giác $ABC$, đường tròn $(K)$ bất kì tiếp xúc với $AB,AC$ lần lượt tại $E,F$. $(K)$ cắt đoạn thẳng $BC$ tại $M,N$ sao cho $M$ nằm giữa $B$ và $M$. $FM$ cắt $EN$ tại $I$. Đường tròn ngoại tiếp $\Delta IFM, IEN$ cắt nhau tại $J$ khác $I$. Chứng minh rằng $IJ$ đi qua $1$ điểm cố định và $KJ \perp IJ$.

Ai có tài liệu về S.O.S cho tớ xin với. Xin chân thành cảm ơn mọi người     

Xem tại đây !

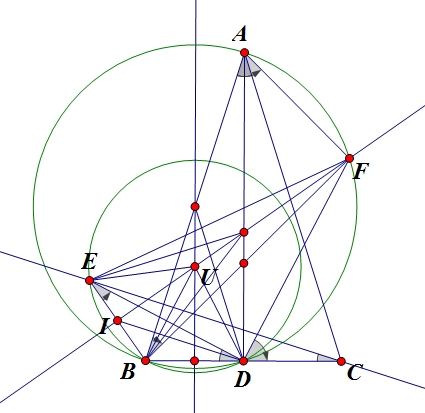
$\boxed{\text{Bài toán 5}}$ Cho $\Delta ABC$ cân tại $A$. Gọi $D$ là trung điểm $BC$. Lấy điểm $E$ ở ngoài tam giác sao cho $CE$ vuông góc với $AB$ và $BD = BE$. Trung trực của đoạn thẳng $BE$ cắt cung nhỏ $AD$ của đường tròn ngoại tiếp $\Delta ABD$ tại $F$.Chứng minh rằng $DE \perp DF$.

 

P/S: Phấn đấu mỗi ngày một bài được giải, cố lên nào ^^!

Giải như sau: (nhìn đề cứ tưởng khó, hóa ra cũng không ảo lắm )

Gọi $I$ là trung điểm của $EP$, $H$ là giao điểm của $CE$ và $AB$. Vẽ đường thẳng $Dx$ vuông góc với $DE$ cắt đường trung trực của $EB$ tại $F'$.

Ta có tứ giác $AHDC$ nội tiếp nên: \[\angle BAD = \angle ECB\]

Lại có: $\angle ECB= \angle IDB$ (do $DI // CE$) nên: \[ \angle BAD = \angle IDB (1)\]

Mà tứ giác $IEF'D$ nội tiếp nên: \[ \angle IDB = \angle EDB - \angle IDE= \angle IED - \angle IDE = \angle IF'D - \angle IF'E = \angle BF'D (2)\]

Từ $(1)$ và $(2)$ suy ra:  \[ \angle BF'D = \angle BAD \]

Nên tứ giác $AF'DB$ nội tiếp đường tròn đường kính $AB$, mà $F,F'$ nằm cùng một nửa mặt phẳng bờ $EB$ nên ta có: \[ F \equiv F' \to DE \perp DF (Q.E.D)\]

$\boxed{\text{Bài toán 6}}$ Cho $\Delta ABC$ nội tiếp đường tròn $(O)$ và ngoại tiếp đường tròn $(I)$. $(I)$ tiếp xúc với $BC,CA,AB$ lần lượt tại $D,E,F$. Gọi $({\omega _a}),({\omega _b}),({\omega _c})$ tiếp xúc với $(I),(O)$ tại $D,K$ (đối với $\omega_a$), tại $E,M$ (đối với $\omega_b$), tại $F,N$ (đối với $\omega_c$). Chứng minh rằng: 

$[1]$ $DK,EM,FN$ đồng quy, gọi điểm đó là $P$.

$[2]$ Trực tâm $\Delta DEF$ nằm trên $OP$.

Cho tam giác ABC cân tại A. Gọi D là trung điểm BC. Lấy điểm E ở ngoài tam giác sao cho CE vuông góc với AB và BD = BE. Trung trực của đoạn thẳng BE cắt cung nhỏ AD của đường tròn ngoại tiếp tam giác ABD tại F. CMR: DE vuông góc với DF

Bài toán này nằm trong mục các bài toán tổng hợp trên diễn đàn Mathlinks.ro, bạn vui lòng trao đổi trong Topic nàynhé!

Nhờ Mod THCS khóa topic này lại, cảm ơn!

___

NLT

$\boxed{\text{Bài toán 5}}$ Cho $\Delta ABC$ cân tại $A$. Gọi $D$ là trung điểm $BC$. Lấy điểm $E$ ở ngoài tam giác sao cho $CE$ vuông góc với $AB$ và $BD = BE$. Trung trực của đoạn thẳng $BE$ cắt cung nhỏ $AD$ của đường tròn ngoại tiếp $\Delta ABD$ tại $F$.Chứng minh rằng $DE \perp DF$.

P/S: Phấn đấu mỗi ngày một bài được giải, cố lên nào ^^!

^{Ai có cuốn vẻ đẹp bất đẳng thức của phạm kim hùng không ạ?}

^{Em nghe nói cuốn đó có nhiều bất đẳng thức từ các cuộc thi IMO lắm đấy}

^{Bác nào có thì cho em mượn nha}

Theo mình biết thì tác giả Phạm Kim Hùng có cuốn sách đầu tay và nổi tiếng nhất là Sáng tạo Bất đẳng thức, làm gì có Vẻ đẹp BĐT ở đây, cuốn đó có lẽ của thầy Trần Phương. 

Còn về Sáng tạo BĐT của PKH, bạn có thể xem ở link đây!

Cho số nguyên dương $n, n>1$ thỏa mãn $3^n-1 \vdots n$. Chứng minh rằng $n \vdots 2$.

$\boxed{\text{Bài toán 4}}$ Cho $\Delta ABC$, lấy $D,E,F$ lần lượt thuộc các cạnh $BC,CA,AB$ sao cho $AD,BE,CF$ đồng quy.$M,D,E$ lần lượt thuộc các cạnh $EF,DF,DE$ sao cho $MD,NE,PF$ đồng quy. Chứng minh rằng: $AM,BN,CP$ đồng quy.

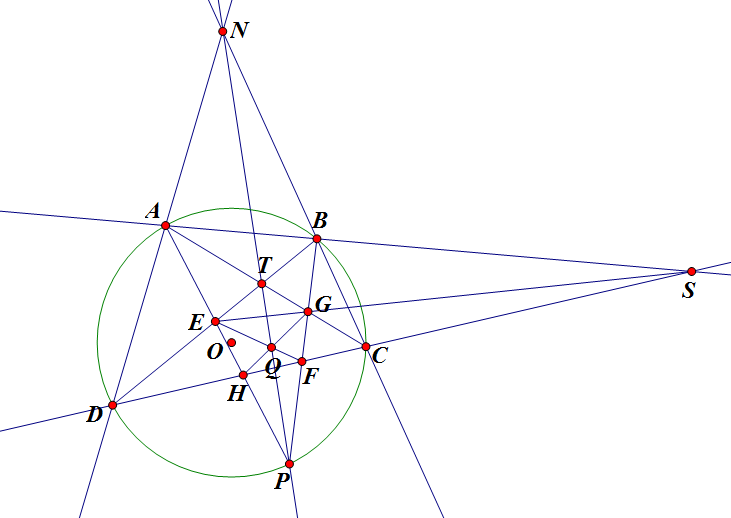
Cho $ABCD$ là tứ giác nội tiếp đường tròn $(O)$ ($AB$ không là đường kính). Gọi $P$ là 1 điểm bất kì trên cung $CD$ không chứa $A,B$. Vẽ $PA$ cắt $DC,DB$ tại $H,E$ tương ứng. Vẽ $PB$ cắt $CD,CA$ tại $F,G$ tương ứng. $HG$ cắt $FE$ tại $Q$.

$T$ là giao điểm của $AC,BD$ còn $S$ là giao điểm của $AB,CD$.

Chứng minh rằng: $P,Q,T$ thẳng hàng $\Leftrightarrow OS \perp PQ$

Giải như sau :

Xét trường hợp $AD$ và $BC$ không song song. Gọi $N$ là giao điểm của chúng.

Khi đó, áp dụng định lý Brocard, ta có: $OS \perp NT$. 

Chứng minh chiều thuận

Ta có $P,Q,T$ thẳng hàng, để chứng minh $OS \perp PQ$ ta đi chứng minh $N,T,Q,P$ thẳng hàng.

Áp dụng định lý Desargues vào $\Delta ATB$ và $\Delta HQF$, ta được: $E,G,S$ thẳng hàng.

Áp dụng định lý Desargues (đảo) vào $\Delta AED$ và $\Delta BGC$ được: $N,T,P$ thẳng hàng.

Từ đó suy ra: $N,T,Q,P$ thẳng hàng $\to ...$.

....

Trường hợp $AD//BC$ chắc đơn giản

P/S: Chiều đảo em còn 1 vướng bận nữa chưa xử được (

___

NLT

Giải phương trình nghiệm nguyên: $(x^2+1)(y^2+1)+4=2(x+1)(y+1)$

Ta có:\[(x^2+ 1)(y^2 + 1) + 4 = 2(x + 1)(y + 1) \Leftrightarrow (y^2 + 1)x^2 - 2(y + 1)x + {y^2} - 2y + 3 = 0( 1)\]

Mà: \[\Delta '\left( 1 \right) = {\left( {y + 1} \right)^2} - ({y^2} - 2y + 3)({y^2} + 1) =  - {y^4} + 2{y^3} - 3{y^2} + 4y - 2\]

Ta chứng minh: $\Delta '(1) \le 0, \forall y \in \mathbb{Z}$. Điều này tương đương với: \[{y^4} - 2{y^3} + 3{y^2} - 4y + 2 \ge 0 \Leftrightarrow {\left( {{y^2} - y} \right)^2} + 2{\left( {y - 1} \right)^2} \ge 0(True)\].

Để tồn tại $x,y$ thì $y=1 \to x=1$

Vậy: \[ \boxed{\text{x=y=1}}\]

P/s: Cũng có thể đánh giá $VT \ge VP$ của phương trình ban đầu, từ đó tìm được các giá trị $x,y$.

___

NLT

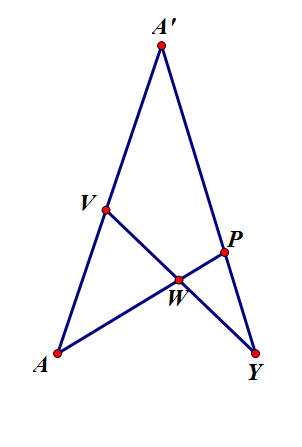
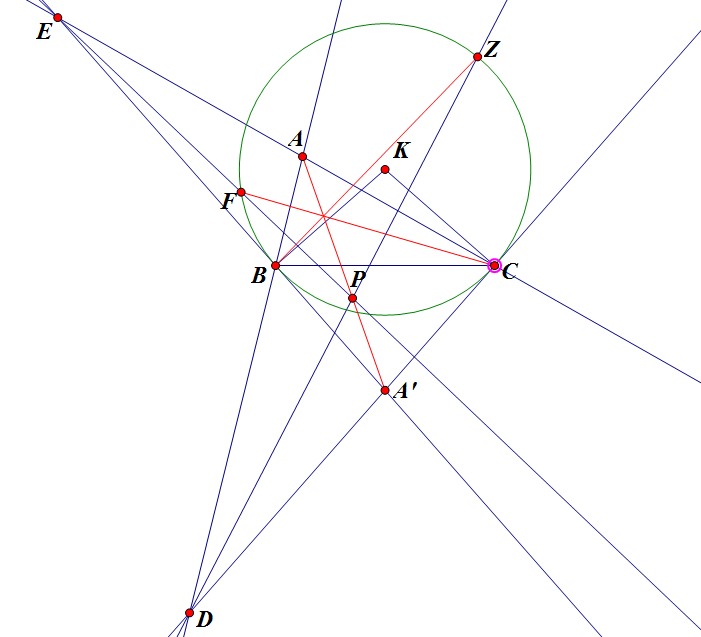
$\boxed{\text{ Bài toán 1 }}$  Cho $\Delta ABC$, đường tròn tâm $K$ tùy ý sao cho $BC$ là dây cung của $(K)$. Gọi $A'$ là giao điểm các tiếp tuyến tại $B$ và $C$ của $(K)$; $D$ là giao điểm của $AB$ và $A'C$, $E$ là giao điểm của $AC$ và $A'B$. Cho $P$ là một điểm tùy ý trên $AA'$; $Z$ và $F$ lần lượt là giao điểm của $DP$ và $EP$ với $(K)$ ($Z,F$ cùng một nửa mặt phẳng bờ $BC$). Chứng minh rằng: $AA'; BZ; CF$ đồng quy.

 

 

Bài 1.png

Hướng nghĩ khác: Cái hình mình chỉnh khá lâu mới được vậy, mong mọi người thông cảm.

Gọi $Q,R$ lần lượt là các giao điểm của $AB,AC$ với $(K)$.

Gọi $P$ là giao điểm của $BZ$ và $CX$ (tại em vẽ hình thiếu tên giao điểm đó, điểm $P$ đề ra có thể cho là điểm $P'$ vậy), $W$ là giao điểm của $RZ$ và $XQ$; $V$ là giao điểm của $BR$ và $CQ$, $Y$ là giao điểm của $BX$ và $CZ$.

Ta đi chứng minh $A, P, A'$ thẳng hàng.

Áp dụng Định lý Pascal cho lục giác nội tiếp đường tròn:

+ Lục giác $BBRCCQ$, ta có: $A', V, A$ thẳng hàng.

+ Lục giác $BBXCCZ$, ta có: $P, A', Y$ thẳng hàng

+ Lục giác $BXQCZR$, ta có: $W, V, Y$ thẳng hàng

+ Lục giác $XQBZRC$, ta có: $W, A, P$ thẳng hàng.

P/s: Ý tưởng của mình mới tới đây thôi, tức là chỉ còn trường hợp dưới đây: (không mất tính tổng quát có thể giả sử thứ tự các điểm như hình dưới)

Giờ em đi ngủ, lúc nào có thời gian em nghĩ tiếp, mọi người nghĩ theo ý tưởng này được không ạ? :| 

P/s: Ý tưởng dùng Desargues cho bài toán này là khá tự nhiên ... Near đã giải quá chuẩn rồi

Sắp thi rồi, có thể mình sẽ ít lên topic này một thời gian, mong mọi người đừng để nó đóng bụi nhé !

___

NLT

$\boxed{\text{ Bài toán 3}}$  Cho $\Delta ABC$, $A_1, B_1,C_1$ lần lượt thuộc các cạnh $BC,CA,AB$. $AA_1, BB_1, CC_1$ lần lượt cắt đường tròn ngoại tiếp tam giác $ABC$ tương ứng tại $A_2,B_2,C_2$. Chứng minh rằng: \[ \frac{AA_{1}}{A_{1}A_{2}}+\frac{BB_{1}}{B_{1}B_{2}}+\frac{CC_{1}}{C_{1}C_{2}}\ge \frac{3p^{2}}{r(4R+r)}\]

Trong đó: $p,r,R$ lần lượt là nửa chu vi, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp của $\Delta ABC$.

$\boxed{\text{ Bài toán 2 }}$  Cho tứ giác $ABCD$ nội tiếp $(O)$. Giả sử $\begin{vmatrix} AD-BC \end{vmatrix} = \begin{vmatrix} AC - BD \end{vmatrix}$. Chứng minh tứ giác $ABCD$ là hình thang cân.

 

Spoiler

Bài này khá là lừa tình

Giải như sau: 

Gọi $M,N,P$ lần lượt là trung điểm của $AB,BD,AC$ lần lượt là trung điểm của $AB,BD,AC$.

Áp dụng công thức đường trung tuyến vào các tam giác $ABC, ADC, BDP$, ta có: \[AB^2 + BC^2+ CD^2 + DA^2= 2(BP^2 + DP^2)+ AC^2= 4NP^2 + AC^2 + BD^2 (1)\]

Theo định lý Ptolemy, ta có: \[AB.CD + AD.BC = AC.BD (2) \to 2AB.CD +2AD.BC = 2AC.BD \]

Lấy $(1)$ trừ $(2)$ vế theo vế ta được: \[{\left( {AB - CD} \right)^2} + {\left( {BC - AD} \right)^2} = {\left( {AC - BD} \right)^2} + 4N{P^2}\]

Kết hợp với giả thiết suy ra: \[{\left( {AB - CD} \right)^2} = 4N{P^2} \Leftrightarrow NP = \frac{1}{2}|AB - CD| = |MN - MP|\]

Theo BĐT tam giác suy ra $MN=MP \to AD=BC$

Vậy $ABCD$ là hình thang cân, phép chứng minh hoàn tất !

___

NLT

Tại sao lại dễ thấy cái đó? Bạn làm tương minh ra thử coi.

Điều này dễ thấy thật mà , ta có:\[f(x) = \sqrt {{x^2} - 7x + 12}  + \sqrt {{x^2} - 9x + 20}  + \sqrt {{x^2} - 8x + 15} \]

\[ \to f'\left( x \right) = \frac{{2x - 7}}{{2\sqrt {{x^2} - 7x + 12} }} + \frac{{2x - 9}}{{2\sqrt {{x^2} - 9x + 20} }} + \frac{{2x - 8}}{{2\sqrt {{x^2} - 8x + 15} }} < 0,\forall x \in [0;3]\]

$\boxed{\text{ Bài toán 1 }}$  Cho $\Delta ABC$, đường tròn tâm $K$ tùy ý sao cho $BC$ là dây cung của $(K)$. Gọi $A'$ là giao điểm các tiếp tuyến tại $B$ và $C$ của $(K)$; $D$ là giao điểm của $AB$ và $A'C$, $E$ là giao điểm của $AC$ và $A'B$. Cho $P$ là một điểm tùy ý trên $AA'$; $Z$ và $F$ lần lượt là giao điểm của $DP$ và $EP$ với $(K)$ ($Z,F$ cùng một nửa mặt phẳng bờ $BC$). Chứng minh rằng: $AA'; BZ; CF$ đồng quy.

GEOMETRY IS A WONDERFUL PART OF MATHEMATICS !

Thân ái chào các bạn !

Thay cho lời mở đầu, mời các bạn vui lòng đọc topic sau!

Các Topic tổng hợp các bài toán trên Mathlinks.ro về các phần Số học, Dãy số - Giới hạn, Phương trình - Hệ phương trình, Phương trình hàm, Đa thức ,... đã được anh Phúc ( dark templar ) lập cách đây không lâu. Hôm nay mình mạn phép lập ra Topic tổng hợp các bài toán Hình học trên diễn đàn Mathlinks.ro .

P/s: Để tăng tính thẩm mỹ, các bạn gửi bài trên đây theo code sau: 

$\boxed{\text{ Bài toán ...}}$ Nội dung bài toán.

Hoặc

CHÚ Ý:  Khoảng từ 4-7 ngày kể từ sau ngày post đề bài, nếu không ai đưa ra lời giải, mình xin trích dẫn lời giải trên Mathlinks.ro. Khi có lời giải cho 1 bài toán, thì sẽ có 1 hoặc 2 bài mới được post lên. Một lưu ý nữa, khi các bạn giải bài cố gắng vẽ hình giúp nhé !

Cùng nổi bão lên nào, chém mạnh tay vào nhé !!!

___

NLT

Chat

Spoiler

@Dark templar: Thật ra lúc đầu anh cũng định lập topic Hình học nhưng mà anh thấy mảng Hình học bên VMF mình có vẻ yếu nên thôi.Cũng may đã có sự góp mặt của các siêu tân binh mới Mà em nhớ bảo các bạn vẽ Hình khi giải bài nhé.

@ NLT:Dạ, nếu họ không vẽ em sẽ ráng vẽ  ^^! Các tân binh mới cũng là lý do để em lập Topic này đó ạ. Có thể với đà này phương châm mỗi tuần 1 bài toán quá anh ơi   

 PQ đi qua trung điểm cung AB (cũng là trung điểm cung CD)

Một cách khác để chứng minh điều này, để ý rằng $IP // MN$ do cùng vuông góc $AB$.

Lại có $\angle QPI = \angle QMN (= \angle QAI = \angle QAN)$.

Từ 2 điều trên có $PQ$ đi qua trung điểm cung $AB$

Anh Định khách sáo quá, mọi người phải cảm ơn Anh đã góp ý mới đúng chứ ạ !
Lần này nâng cấp có một số thứ ở phiên bản trước không tương thích, trong đó có những thứ mà anh Định nói.
Mọi người thấy tiếng Anh ở đâu thì cũng xin vui lòng báo với BQT để dịch ra tiếng Việt (và nếu thấy dùng tiếng Việt chưa được hay thì góp ý để thay đổi  ).
Xin cảm ơn mọi người.

Hình như lệnh 

	Spoiler 
	
...
 

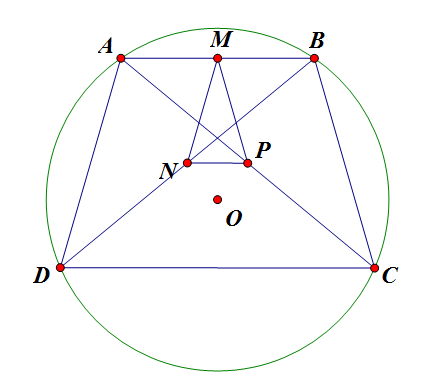
Cho hình thang $ABCD$ nội tiếp đường tròn $(O)$, đáy lớn $CD$, $H$ là trung điểm $CD$. Gọi $I,J,K$ lần lượt là tâm đường tròn nội tiếp của $\Delta ACD, \Delta AHD, \Delta AHC$. Đường tròn đường kính $AI$ cắt $(O)$ tại $Q$ và cắt $AB$ tại $P$. Chứng minh rằng $PQ, (O)$ và đường tròn ngoại tiếp $\Delta AKJ$ cùng đi qua $1$ điểm. 

___

NLT

tài liệu mình đọc có phân nhóm các lời giải, và mình biết có đến 51 cách chứng minh lận

Thế thì thay vì post cách 1, cách 2, cách 3,... bạn có thể up tài liệu đó lên diễn đàn để mọi người cùng học tập, có ích hơn là gõ $\LaTeX$ trong 1 topic như thế này, sẽ mất nhiều thời gian và công sức lắm bạn ạ

Spoiler

 Còn nếu bạn không có ebook, có thể chia sẻ với mọi người tên, hoặc bìa của cuốn sách. Nếu nó quá hiếm, chúng ta có thể trao đổi trực tiếp qua bưu điện , hì hì  

___

NLT

Sau khi đọc xong một vài quyển sách có nói về BĐT Nesbitt, mình xin chia sẻ với diễn đàn một số cách chứng minh BĐT này:

Đề bài: Chứng minh với mọi a, b, c >0 thì:

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \frac{3}{2}$.

( sách  Những con đường khám phá lời giải Bất đẳng thức-NXB Sư phạm-chương 5)

Cách 1:

Thực sự trên mạng đã nói nhiều về vấn đề này, và đã có rất nhiều cách chứng minh Nesbitt, xem tại đây !

___

NLT

Đây có thể là một phương pháp khá quen thuộc nhưng cũng lạ lẫm với một số người, do viết lời nói đầu không hay nên mình xin đi vào vấn đề luôn và chia sẻ link sau(có thể có bạn đã có rồi   ) 

Phương pháp pqr

Đây là phương pháp đánh giá tích, chỉ cần nắm vững đạo hàm và một số biến đổi thì bất đẳng thức đối xứng nào cũng có thể giải được. Các định lí trong phương pháp này sẽ giúp bài toán trở nên đơn giản hơn khi quy về được một hàm $f(abc,ab+bc+ac,a+b+c)$ nếu thuần nhất thì hoàn toàn có thể quy về 1 biến (khá đơn giản)

Nếu có trùng lặp mong các bạn thông báo 

Đây là phương pháp ABC mà bạn? Có gì nhầm lẫn chăng? Bạn đọc post này và kiểm tra lại, nếu đúng thì sửa lại tiêu đề nhé ! 

___

NLT