Cho x,y,z>0 thỏa mãn x+y+z=1. Chứng minh $\sqrt{x^{2}+2y^{2}}+\sqrt{y^{2}+2z^{2}}+\sqrt{z^{2}+2x^{2}} \geq \sqrt{3}$
Jiki Watanabe nội dung
Có 63 mục bởi Jiki Watanabe (Tìm giới hạn từ 29-04-2020)
#695379 Chứng minh $\sqrt{x^{2}+2y^{2}}+...
 Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:53
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:53
trong
Bất đẳng thức và cực trị
#695378 Chứng minh rằng $x^{2}+y^{2}\leq 2$
 Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:47
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:47
trong
Bất đẳng thức và cực trị
Cho $x^{2}+y^{3} \geq x^{3}+y^{4}$. Chứng minh rằng $x^{2}+y^{2}\leq 2$
#695376 Chứng minh
 Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:33
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Jiki Watanabe
on 24-10-2017 - 20:33
trong
Bất đẳng thức và cực trị
Cho x,y>0 thỏa mãn x2+x3 $\geq$ x3+x4. Chứng minh x3+y3 $\leq$ 2
#693939 Biết $\alpha+\beta +\gamma=360^{\circ}...
 Đã gửi bởi
Jiki Watanabe
on 29-09-2017 - 23:22
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 29-09-2017 - 23:22
trong
Hình học
Về phía ngoài tam giác ABC dựng các tam giác AMB, BNC, CPA cân có số đo các góc ở đỉnh là AMB $=\alpha $; BNC$=\beta$; CPA$=\gamma $. Biết $\alpha+\beta +\gamma=360^{\circ}$. Tính số đo ba góc của tam giác MNP.
#693626 $1+\frac{1}{\sqrt[3]{2}}+\f...
 Đã gửi bởi
Jiki Watanabe
on 24-09-2017 - 10:21
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 24-09-2017 - 10:21
trong
Đại số
Chứng minh: $1+\frac{1}{\sqrt[3]{2}}+\frac{1}{\sqrt[3]{3}}+\frac{1}{\sqrt[3]{4}}+...+\frac{1}{\sqrt[3]{2009}}>237$
#693201 Tính tỉ số giữa các cạnh của tam giác ABC
 Đã gửi bởi
Jiki Watanabe
on 17-09-2017 - 13:40
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 17-09-2017 - 13:40
trong
Hình học
Cho tam giác ABC vuông tại A. Lấy E là trung điểm của BC. I là tâm đường tròn nội tiếp tam giác ABC. Biết tam giác IEC vuông. Tính tỉ số giữa các cạnh của tam giác ABC.
#693200 Cho đường tròn (O) nội tiếp tam giác ABC
 Đã gửi bởi
Jiki Watanabe
on 17-09-2017 - 13:36
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 17-09-2017 - 13:36
trong
Hình học
Cho tam giác ABC và đường tròn (O) nội tiếp tam giác. (O) tiếp xúc với BC tại D. Kẻ đường kính DON. Tiếp tuyến tại N cắt AB, AC tại I, K. Gọi giao điểm của AN với BC là F. Chứng minh rằng BD=CF
#692157 Tìm giá trị nhỏ nhất của tổng
 Đã gửi bởi
Jiki Watanabe
on 02-09-2017 - 22:08
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 02-09-2017 - 22:08
trong
Đại số
Cho bảng hình vuông kích thước 10x10 được chia thành 100 ô vuông nhỏ. Người ta viết các số tự nhiên từ 1 đến 100 theo trình tự sau:
- Hàng T1, từ trái sang, viết các số từ 1 đến 10
- Hàng T2, từ trái sang, viết các số từ 11 đến 20
- ....
Cứ như vậy cho đến hết. Sau đó cắt bảng thành các hình chữ nhật có kích thước 2x1 hoặc 1x2. Tính tích của 2 số trong hình chữ nhật nhỏ rồi cộng 50 tích lại với nhau.
Cần phải cắt như thế nào để tổng đó nhỏ nhất và nhỏ nhất là bao nhiêu?
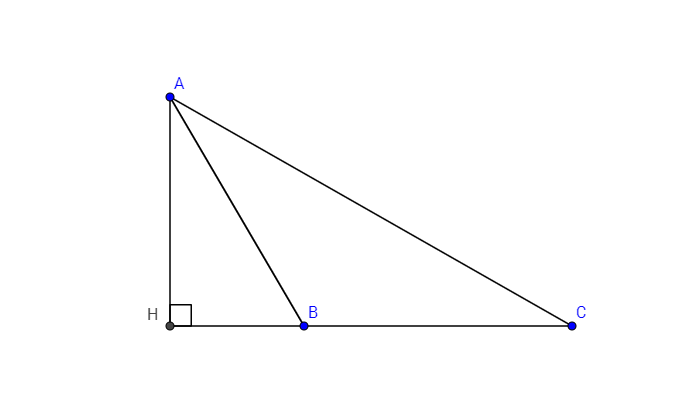
#691535 Tìm H để $P_{HOC}$ đạt giá trị lớn nhất.
 Đã gửi bởi
Jiki Watanabe
on 25-08-2017 - 21:10
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 25-08-2017 - 21:10
trong
Hình học
Cho $(O;r)$, đường kính AB. $H \in OA$. Dây CD vuông góc với AB tại H. Xác định vị trí của H để chu vi tam giác HOC lớn nhất.
#691155 $\sqrt{2+\sqrt{2+\sqrt{3}}}...
 Đã gửi bởi
Jiki Watanabe
on 20-08-2017 - 20:26
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 20-08-2017 - 20:26
trong
Đại số
Tính $\sqrt{2+\sqrt{2+\sqrt{3}}}-\sqrt{6-3\sqrt{2+\sqrt{3}}}$
#690592 $\frac{3}{\sqrt{x}+\sqrt{y...
 Đã gửi bởi
Jiki Watanabe
on 15-08-2017 - 17:14
trong
Phương trình, hệ phương trình và bất phương trình
Đã gửi bởi
Jiki Watanabe
on 15-08-2017 - 17:14
trong
Phương trình, hệ phương trình và bất phương trình
thực ra đây là 1 bất đẳng thức dấu bằng xảy ra khi x=4;y=9 mà hình như đề bị sai
$\frac{3}{\sqrt{x}+\sqrt{y}}+\frac{\sqrt{x}}{\sqrt{y}+2}+\frac{\sqrt{y}}{5}+\frac{2}{\sqrt{x}+3}= 2$
có thể là giải phương trình bằng phương pháp bất đẳng thức thì sao ạ .-.
#690572 $\frac{3}{\sqrt{x}+\sqrt{y...
 Đã gửi bởi
Jiki Watanabe
on 15-08-2017 - 10:36
trong
Phương trình, hệ phương trình và bất phương trình
Đã gửi bởi
Jiki Watanabe
on 15-08-2017 - 10:36
trong
Phương trình, hệ phương trình và bất phương trình
Giải phương trình: $\frac{3}{\sqrt{x}+\sqrt{y}}+\frac{\sqrt{y}}{\sqrt{y}+2}+\frac{\sqrt{y}}{5}+\frac{2}{\sqrt{x}+3}=2$
#690482 Chứng minh M di động trên đường tròn cố định
 Đã gửi bởi
Jiki Watanabe
on 14-08-2017 - 09:22
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 14-08-2017 - 09:22
trong
Hình học
Cho $(O;R)$. A cố định nằm trên đường tròn, B di động nằm trên đường tròn. $M \in AB$ sao cho $AM= \frac{2}{3} AB$. Chứng minh M di động trên đường tròn cố định. Tính bán kính đường tròn đó.
#689881 Topic phương trình, hệ phương trình vô tỉ
 Đã gửi bởi
Jiki Watanabe
on 07-08-2017 - 23:26
trong
Phương trình, hệ phương trình và bất phương trình
Đã gửi bởi
Jiki Watanabe
on 07-08-2017 - 23:26
trong
Phương trình, hệ phương trình và bất phương trình
Bài 126:
Giải phương trình: $\sqrt{x(x-1)}+\sqrt{x(x+2)}=2\sqrt{x^2}$.
ĐKXĐ: $x\geq 1$ hoặc $x=0$ hoặc $x\leq -2$
- Xét $x=0$ ta được $x=0$ là nghiệm của phương trình
- Xét $x\geq 1$ ta có:
pt$\Leftrightarrow \sqrt{x-1}+\sqrt{x+2}=2\sqrt{x}$
$\Leftrightarrow x-1+x+2+2\sqrt{(x-1)(x+2)}=4x$
$\Leftrightarrow 2x-1=2\sqrt{(x+1)(x+2)}$ $(x\geq 0,5)$
$\Leftrightarrow 4x^2-4x+1=4x^2+4x-8$
$\Leftrightarrow x=\frac{9}{8}$ (TM)
- Xét $x\leq -2$ ta có:
pt$\Leftrightarrow \sqrt{1-x}+\sqrt{-x-2}=2\sqrt{-x}$
$\Leftrightarrow 1-x-x-2+2\sqrt{(1-x)(-x-2)}=-4x$
$\Leftrightarrow -2x+1=2\sqrt{x^2+x-2}$ $(x\leq 0,5)$
$\Leftrightarrow 4x^2-4x+1=4x^2+4x-8$
$\Leftrightarrow x=\frac{9}{8}$ (L)
Vậy tập nghiệm của phương trình là $S=\left \{ 0;\frac{9}{8} \right \}$
#689791 Cho tam giác ABC nhọn nội tiếp (O;r)
 Đã gửi bởi
Jiki Watanabe
on 06-08-2017 - 23:58
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 06-08-2017 - 23:58
trong
Hình học
#689790 $A=a^2+\sqrt{a^4+a+1}$
 Đã gửi bởi
Jiki Watanabe
on 06-08-2017 - 23:43
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 06-08-2017 - 23:43
trong
Đại số
Cho $a=\frac{1}{2}\sqrt{\sqrt{2}+\frac{1}{8}}-\frac{\sqrt{2}}{8}$. Tính $A=a^2+\sqrt{a^4+a+1}$
#688420 Chứng minh góc B và C nhọn
 Đã gửi bởi
Jiki Watanabe
on 23-07-2017 - 16:34
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 23-07-2017 - 16:34
trong
Hình học
#688268 Topic phương trình, hệ phương trình vô tỉ
 Đã gửi bởi
Jiki Watanabe
on 21-07-2017 - 21:01
trong
Phương trình, hệ phương trình và bất phương trình
Đã gửi bởi
Jiki Watanabe
on 21-07-2017 - 21:01
trong
Phương trình, hệ phương trình và bất phương trình
Ăn nhẹ tí nhỉ
Bài 150: $x-4\sqrt{2x+2}-2\sqrt{2-x}+9=0$
#688214 Chứng minh góc B và C nhọn
 Đã gửi bởi
Jiki Watanabe
on 21-07-2017 - 10:22
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 21-07-2017 - 10:22
trong
Hình học
Cho tam giác ABC có BC=14, đường cao AH=12 và AC+AB=28.
a) Chứng minh góc B và C nhọn
b) Tính AB, AC
#687199 Chứng minh rằng nếu $PF \perp DQ$ thì AP=BC
 Đã gửi bởi
Jiki Watanabe
on 11-07-2017 - 09:43
trong
Hình học
Đã gửi bởi
Jiki Watanabe
on 11-07-2017 - 09:43
trong
Hình học
Cho hình chữ nhật $ABCD$ có $FA=FB (F\in AB)$. $P$ nằm trên tia phân giác góc C. $PQ\perp BC$ (Q$\in$BC). Chứng minh rằng nếu $PF \perp DQ$ thì $AP=BC$
#686512 Min $A=\sqrt{x^3+2(1+\sqrt{x^3+1})}+\...
 Đã gửi bởi
Jiki Watanabe
on 04-07-2017 - 23:07
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Jiki Watanabe
on 04-07-2017 - 23:07
trong
Bất đẳng thức và cực trị
Tìm giá trị nhỏ nhất của biểu thức $A=\sqrt{x^3+2(1+\sqrt{x^3+1})}+\sqrt{x^3+2(1-\sqrt{x^3+1})}$
#686047 Chứng minh tồn tại một số dương trong hai số $2a+b-2\sqrt{cd...
 Đã gửi bởi
Jiki Watanabe
on 30-06-2017 - 20:17
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 30-06-2017 - 20:17
trong
Đại số
Cho $a,b,c,d > 0$. Chứng minh tồn tại một số dương trong hai số $2a+b-2\sqrt{cd}$ và $2c+d-2\sqrt{ab}$
#685778 ĐỊNH ĐỀ GOLDBACH
 Đã gửi bởi
Jiki Watanabe
on 27-06-2017 - 23:40
trong
Toán học lý thú
Đã gửi bởi
Jiki Watanabe
on 27-06-2017 - 23:40
trong
Toán học lý thú
Ta có 8 nhóm số nguyên tố “Hưng Phú” như sau:
A1 là tập hợp những số lẻ, có chữ số tận cùng là 1 và chia 3 dư 1.
A3 là tập hợp những số lẻ, có chữ số tận cùng là 3 và chia 3 dư 1.
A7 là tập hợp những số lẻ, có chữ số tận cùng là 7 và chia 3 dư 1.
A9 là tập hợp những số lẻ, có chữ số tận cùng là 9 và chia 3 dư 1.
B1 là tập hợp những số lẻ, có chữ số tận cùng là 1 và chia 3 dư 2.
B3 là tập hợp những số lẻ, có chữ số tận cùng là 3 và chia 3 dư 2.
B7 là tập hợp những số lẻ, có chữ số tận cùng là 7 và chia 3 dư 2.
B9 là tập hợp những số lẻ, có chữ số tận cùng là 9 và chia 3 dư 2.
P (Prime) là tập hợp các số nguyên tố.
Gọi S = A1 A3 A7 A9 B1 B3 B7 B9.
Thì ta có các phát biểu sau:
Thứ nhất: Tập hợp P chắc chắn phải là tập con của tập hợp S, hoặc nói cách khác, tập hợp P chắc chắn phải chứa trong tập hợp S; hoặc nói cách khác nữa, mọi phần tử của tập hợp P đều là phần tử của tập hợp S.
$2\in P$ nhưng $2\notin S$
?? ![]() ??
??
#685766 Chứng minh $\frac{a+(\sqrt{a}-\sqrt{c...
 Đã gửi bởi
Jiki Watanabe
on 27-06-2017 - 20:39
trong
Đại số
Đã gửi bởi
Jiki Watanabe
on 27-06-2017 - 20:39
trong
Đại số
Cho $a,b,c>0$ thỏa mãn $\sqrt{a}+\sqrt{b}\neq \sqrt{c}$ và $ab=(\sqrt{a}+\sqrt{b}-\sqrt{c})^2$
Chứng minh rằng $\frac{a+(\sqrt{a}-\sqrt{c})^2}{b+(\sqrt{b}-\sqrt{c})^2}=\frac{\sqrt{a}-\sqrt{c}}{\sqrt{b}-\sqrt{c}}$
- Diễn đàn Toán học
- → Jiki Watanabe nội dung