Hihi, ôn thi kiểu này hiệu quả nhỉ, 100% đỗRất nhiều người sử dụng tài liệu này để ôn văn
le_hoang1995 nội dung
Có 342 mục bởi le_hoang1995 (Tìm giới hạn từ 29-04-2020)
#342014 Tài liệu ôn thi có 1-0-2
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 20:58
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 20:58
trong
Quán hài hước
#341863 Chứng minh: $a^r(a^2-b^2)(c+a)+b^r(b^2-c^2)(a+b)+c^r(c^2-a^2)(b+c)\...
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 13:32
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 13:32
trong
Bất đẳng thức và cực trị
Không mất tổng quát, giả sử a là số lớn nhất.1. Với $a,b,c,r\geq 0$ chứng minh bất đẳng thức sau
$a^r(a^2-b^2)(c+a)+b^r(b^2-c^2)(a+b)+c^r(c^2-a^2)(b+c)\geq 0$
Xét hàm số $f(a)=VT$
$$f'(a)=r.a^{r-1}(a^2-b^2)(a+c)+2a^{r+1}(a+c)+a^r(a^2-b^2)+b^r(b^2-c^2)-2ac^r(b+c)$$ Dễ thấy $f'(a) \ge 0$ vì $2a^{r+1}(a+c)\geq 2ac^r(b+c)$. Suy ra hàm số đồng biến.
TH1 $a\ge b\ge c$. $$\Rightarrow f(a)\ge f(b)=2b^{r+1}(b^2-c^2)+c^r(c^2-b^2)(b+c)=(b^2-c^2)(2b^{r+1}-bc^r-c^{r+1})\geq 0$$
TH2 $a\ge c\ge b$ $$\Rightarrow f(a)\geq f©=2c^{r+1}(c^2-b^2)+b^r(b^2-c^2)(c+b)=(c^2-b^2)(2c^{r+1}-b^rc-b^{r+1})\geq 0$$
ĐPCM
#341839 Chứng minh góc $O_1$=$O_2$
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 12:21
trong
Hình học
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 12:21
trong
Hình học
Đường thẳng Ox và Oy cắt hai đường tròn tại bốn điểm $A_1,A_2,A_3,A_4$ và $B_1,B_2,B_3,B_4$ như hình vẽ. Các đường thằng $A_1,B_1$ giao với $A_2,B_2$ tại $O_1$; $A_3,B_3$ giao với $A_4,B_4$ tại $O_2$
Chứng minh góc $O_1$=$O_2$
Có $ \widehat{O_{1}B_{2}B_{1}}=\widehat{O_{2}A_{3}A_{4}}$ Do tứ giác $A_2A_3B_3B_2$ nội tiếp.Tại sao lại có đoạn:
$ 180^o - \widehat{O_{1}B_{1}B_{2}}-\widehat{O_{1}B_{2}B_{1}}$
$= 180^o - \widehat{O_{2}A_{3}A_{4}}-\widehat{O_{2}A_{4}A_{3}}$
?
Và $\widehat{O_{1}B_{1}B_{2}}=\frac{1}{2}sd\widetilde{A_1B_4}=\frac{1}{2}.(360-sd\widetilde{A_1B_1B_4})=180-\frac{1}{2}sd\widetilde{A_1B_1B_4}=180-\widehat{A_1A_4B_4}=\widehat{O_2A_4A_3}$
#341744 Sáng tạo BĐT liên quan đến các bộ trội-chứng minh và ứng dụng
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 01:14
trong
Tài liệu, chuyên đề, phương pháp về Bất đẳng thức
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 01:14
trong
Tài liệu, chuyên đề, phương pháp về Bất đẳng thức
Phần III Một số đại lượng trung bình.
1. Bài toán mở đầuBài toán sau đâu khá quen thuộc: Cho các số thực dương $a_1,a_2,...,a_n$ và số thực $k\ge1$.Chứng minh rằng:
$$\frac{a_1^k+a_2^k+...+a_n^k}{n}\geq \left ( \frac{a_1+a_2+...+a_n}{n} \right )^k$$
Cách chứng minh cho bài toán này không khó lắm, chúng ta chỉ cần áp dụng BĐT Jensen cho hàm số lồi $f(a)=a^k$ với $ k \ge 1$ là được.
Từ bài toán trên, chúng ta đi tìm một hướng mở rộng hơn cho nó, để dễ dàng nhất, ta đi đến bài toán sau:
2. Các bài toán.
Bài 1. (Đào Thanh Oai- Lê Văn Hoàng).Cho hai dãy số thực dương thỏa mãn $a_1 \ge a_2 \ge ...\ge a_n \ge 1$ và $x_1 \ge x_2 \ge ... \ge x_n \ge1$. Chứng minh BĐT:
$$\frac{a_1^{x_1}+a_2^{x_2}+...+a_n^{x_n}}{n} \ge \left ( \frac{a_1+a_2+...+a_n}{n} \right )^{\frac{x_1+x_2+...+x_n}{n}}$$
Chứng minh:
Xét dãy số giảm $a_1 \ge a_2 \ge ... \ge a_k \ge ... \ge a_n\ge 1$ và dãy số giảm $x_1 \ge x_2 \ge ... \ge x_k \ge ... \ge x_n \ge 1$
Xét hàm số các hàm số dạng $f_k(t)=a_k^{t}$ với $t \ge1; a_k \ge 1$. Các hàm số này lồi và $f_k'(x_0)=a_k^{x_0}.lna_k \geq a_{k+1}^{x_0}.lna_{k+1}= f'_{k+1}(x_0)$.
Nên các hàm số thỏa mãn tính chất của định lý mở rộng bất đẳng thức karamata.
Xét hai bộ số $(x_1,x_2,...,x_n)$ và $ \left ( x,x,...,x \right )$ trong đó $x=\frac{x_1+x_2+...+x_n}{n}$
Dễ thấy ta luôn có $$\frac{x_1+x_2+...+x_k}{k}\geq \frac{x_1+x_2+...+x_k+x_{k+1}}{k+1}\geq ...\geq \frac{x_1+x_2+...+x_n}{n}$$ $$\Rightarrow x_1+x_2+...+x_k\geq k.\frac{x_1+x_2+...+x_n}{n}=k.x=x+x+...+x$$
Vậy hai bộ số $(x_k)$ và $(x)$ trên cũng thỏa mãn định lý mở rộng bất đẳng thức karamata.
Như vậy, ta chỉ cần áp dụng định lý trên
$f_1(x_1)+f_2(x_2)+....f_n(x_n)\geq f_1(x)+f_2(x)+....f_n(x)$
$$\Rightarrow a_1^{x_1}+a_2^{x_2}+...+a_n^{x_n}\geq a_1^x+a_2^x+...+a_n^x$$ $$\Rightarrow \frac{a_1^{x_1}+a_2^{x_2}+...+a_n^{x_n}}{n}\geq \frac{a_1^x+a_2^x+...+a_n^x}{n}$$
Theo một kết quả quen thuộc, ta có $$\frac{b_1^t+b_2^t+...+b_n^t}{n}\geq \left ( \frac{b_1+b_2+...+b_n}{n} \right )^t$$ với $ t \ge1$.
Áp dụng vào bài trên ta được $$ \frac{a_1^x+a_2^x+...+a_n^x}{n}\geq \left ( \frac{a_1+a_2+...+a_n}{n} \right )^x$$ (vì dễ thấy $x \ge 1$)
Suy ra $$\Rightarrow \frac{a_1^{x_1}+a_2^{x_2}+...+a_n^{x_n}}{n}\geq \left ( \frac{a_1+a_2+...+a_n}{n} \right )^x$$
_________________________________________________________________
Còn 1 cách nữa để chứng minh bài toán trên, sử dụng 1 BĐT của anh Đào Thanh Oai tại đây
(Coi bộ $(x_k)$ thành bộ $(b_k)$)
Với $a_1 \geq a_2 \geq ......\geq a_n \geq 1$ hoặc $1 \geq a_n \geq a_{n-1} ......\geq a_1 \geq 0$ và $b_1 \geq b_2 \ .... \geq b_n \geq 0$ Ta có bất đẳng thức:
$(b_1+b_2+...+b_n)(a_1^{b_1}+.....+a_n^{b_n})\geq b_1(a_1^{b_1}+a_1^{b_2}.....+a_1^{b_n})+.....+b_n(a_n^{b_1}+.....+a_n^{b_n}) $
Dấu bằng xảy ra khi và chỉ khi hoặc:
$a_1=a_2 = ......= a_n$ hoặc $b_1=b_2 = ......= b_n$
Đặt $\frac{b_1+b_2+...+b_n}{n}=b$
Sử dụng BĐT AM-GM và BĐT Chê-bư sép cho 2 bộ đơn điệu cùng chiều trên, ta được
$(b_1+b_2+...+b_n)(a_1^{b_1}+.....+a_n^{b_n})\geq b_1(a_1^{b_1}+a_1^{b_2}.....+a_1^{b_n})+.....+b_n(a_n^{b_1}+.....+a_n^{b_n})$
$\geq b_1.n.a_1^{b}+b_2.n.a_2^{b}+...+b_n.n.a_n^{b}$
$=n\left [ b_1.a_1^{b}+b_2.a_2^{b}+...+b_n.a_n^{b} \right ]$
$\geq n.\frac{1}{n}.(b_1+b_2+...+b_n).\left [ a_1^{b}+a_2^{b}+...+.a_n^{b} \right ]$
$\Rightarrow (b_1+b_2+...+b_n)(a_1^{b_1}+.....+a_n^{b_n})\geq(b_1+b_2+...+b_n)\left [ a_1^{b}+a_2^{b}+...+.a_n^{b} \right ]$
$\Rightarrow a_1^{b_1}+.....+a_n^{b_n}\geq a_1^{b}+a_2^{b}+...+.a_n^{b}$
$\Rightarrow \frac{a_1^{b_1}+.....+a_n^{b_n}}{n}\geq \frac{a_1^{b}+a_2^{b}+...+.a_n^{b}}{n}$
Theo một kết quả quen thuộc, ta có
$$\frac{x_1^k+x_2^k+...+x_n^k}{n}\geq \left ( \frac{x_1+x_2+...+x_n}{n} \right )^k$$.
Áp dụng vào trên ta được
$$\frac{a_1^{b}+a_2^{b}+...+.a_n^{b}}{n}\geq \left ( \frac{a_1+a_2+...+a_n}{n} \right )^{b}$$
Suy ra $$\frac{a_1^{b_1}+.....+a_n^{b_n}}{n}\geq \left ( \frac{a_1+a_2+...+a_n}{n} \right )^{b}$$
Dấu bằng xảy ra khi $$\left\{\begin{matrix}
a_1=a_2=..=a_n\\b_1=b_2=...=b_n
\end{matrix}\right.$$
Bài toán 2 ( Lê Văn Hoàng) Cho $a_1 \ge a_2 \ge ... \ge a_n >0$ và $ x_1 \ge x_2 \ge... \ge x_n>0$. Chứng minh bất đẳng thức:
$$a_1^{x_1}.a_2^{x_2}...a_n^{x_n}\geq \left ( a_1.a_2...a_n \right )^{\frac{x_1+x_2+...+x_n}{n}}$$
Giải:
Trước hết, ta chứng minh BĐT sau:
Với $(x_k)$ và $(a_k)$ là hai bộ giảm thì ta có $$a_1^{x_1}...a_n^{x_n}\geq a_1^{x_{k1}}.a_2^{x_{k2}}...a_n^{x_{kn}}$$.
Trong đó $x_{k1}, x_{k2},...$ là một hoán vị bất kì của dãy $x_k$
Thật vậy, lấy logarit tự nhiên hai vế, ta cần chứng minh $$x_1.lna_1+x_2.lna_2+...+x_n.lna_n\geq x_{k1}.lna_1+...+x_{kn}.lna_n$$.
Nhưng nó đúng theo BĐT hoán vị
____________________________
Xét các bộ số $(x_1,x_2,...,x_n)$ với $x_1 \ge x_2 \ge ... \ge x_n$ và $(b,b,b...,b)$ $b=\frac{x_1+x_2+...+x_n}{n}$
Dễ thấy ta có $(x_k)\gg (b)$
Áp dụng BĐT Muihard ta có $$\sum a_1^{x_{k1}}.a_2^{x_{k2}}...a_n^{x_{kn}}\geq \sum a_1^{b_{k1}}a_2^{b_{k2}}...a_n^{b_{kn}}$$
$$=n!.\left ( a_1.a_2...a_n \right )^{b}$$
Lại theo bổ đề trên $$ n!.a_1^{x_1}.a_2^{x_2}...a_n^{x_n} \ge \sum a_1^{x_{k1}}.a_2^{x_{k2}}...a_n^{x_{kn}}$$
Suy ra $$a_1^{x_1}.a_2^{x_2}...a_n^{x_n}\geq \left ( a_1.a_2...a_n \right )^b \ge \left ( a_1.a_2...a_n \right )^{\frac{x_1+x_2+...+x_n}{n}}$$
__________________________________
Áp dụng kết quả bài toán trên, ta thay tương ứng $(x_k)$ bằng $(a_k)$, ta thu được bài toán:
$$a_1^{a_1}.a_2^{a_2}...a_n^{a_n}\geq (a_1a_2...a_n)^{\frac{a_1+a_2+...+a_n}{n}}$$
Nhưng ta còn biết 1 kết quả mạnh hơn bài toán trên:
$$a_1^{a_1}.a_2^{a_2}...a_n^{a_n}\geq\left ( \frac{a_1+a_2+...+a_n}{n} \right ) ^{a_1+a_2+...+a_n}\geq (a_1a_2...a_n)^{\frac{a_1+a_2+...+a_n}{n}}$$
Như vậy liệu ta có thể có:
$$a_1^{x_1}.a_2^{x_2}...a_n^{x_n}\geq\left ( \frac{a_1+a_2+...+a_n}{n} \right )^{\frac{x_1+x_2+...+x_n}{n}}$$
??????????????????????
#341734 Hài :D
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 00:27
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 00:27
trong
Quán hài hước
#341733 Hài :D
 Đã gửi bởi
le_hoang1995
on 30-07-2012 - 00:25
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 30-07-2012 - 00:25
trong
Quán hài hước
#341713 $$\frac{1}{a}+\frac{a}{b}+ab^2 \ge \sqrt{3(1+a^...
 Đã gửi bởi
le_hoang1995
on 29-07-2012 - 23:22
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
le_hoang1995
on 29-07-2012 - 23:22
trong
Bất đẳng thức - Cực trị
http://onluyentoan.v...read.php?t=6794
#341707 ĐK để $x_1y_1+....+x_ny_n\geq (y_1+y_2+...+y_n)\sqrt[n]{x...
 Đã gửi bởi
le_hoang1995
on 29-07-2012 - 23:12
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
le_hoang1995
on 29-07-2012 - 23:12
trong
Bất đẳng thức - Cực trị
Mọi người xem thử hộ em xem có sai lầm gì không nhé, lần đầu tiên em sử dụng các BĐT kiểu như thế này nên sợ có gì đó chưa hiểu rõ bản chất của nó. Cho font to lên nhé, tại vì toàn có số mũ thôi.$\alpha _1\geq \alpha _2\geq ...\geq \alpha _n>0;$
$ \alpha _1+\alpha _2+...+\alpha _n=1;$
Với $x_1\geq x_2\geq ...\geq x_n>0$
$x_1^{\alpha _1}.x_2^{\alpha _2}..x_n^{\alpha _n}\geq \sqrt[n]{x_1x_2...x_n}$.
Trước hết, ta chứng minh BĐT sau:
Với $(x_k)$ và $(a_k)$ là hai bộ giảm thì ta có $$x_1^{a_1}...x_n^{a_n}\geq x_1^{a_{k1}}.x_2^{a_{k2}}...x_n^{a_{kn}}$$.
Trong đó $a_{k1}, a_{k2},...$ là một hoán vị bất kì của dãy $a_k$
Thật vậy, lấy logarit tự nhiên hai vế, ta cần chứng minh $$a_1.lnx_1+a_2.lnx_2+...+a_n.lnx_n\geq a_{k1}.lnx_1+...+a_{kn}.lnx_n$$.
Nhưng nó đúng theo BĐT hoán vị
____________________________
Xét các bộ số $(a_1,a_2,...,a_n)$ với $a_1 \ge a_2 \ge ... \ge a_n$ và (b,b,b...,b) $b=\frac{a_1+a_1+...+a_n}{n}=\frac{1}{n}$.
Ta có bộ a trội hơn bộ b ( trong sách STBDT trang 321)
Áp dụng BĐT Muihard ta có $$\sum x_1^{a_{k1}}.x_2^{a_{k2}}...x_n^{a_{kn}}\geq \sum x_1^{b_{k1}}x_2^{b_{k2}}...x_n^{b_{kn}}$$
$$=n!.\left ( x_1.x_2...x_n \right )^{\frac{1}{n}}=n!.\sqrt[n]{x_1.x_2...x_n}$$
LẠi theo bổ đề em vừa làm trên $$ n!.x_1^{a_1}.x_2^{a_2}...x_n^{a_n} \ge \sum x_1^{a_{k1}}.x_2^{a_{k2}}...x_n^{a_{kn}}$$
Suy ra $$ x_1^{a_1}.x_2^{a_2}...x_n^{a_n} \ge \sqrt[n]{x_1.x_2...x_n}$$
#341630 GTNN của $P$ theo $a, b$ với : $$ P = \su...
 Đã gửi bởi
le_hoang1995
on 29-07-2012 - 21:13
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
le_hoang1995
on 29-07-2012 - 21:13
trong
Bất đẳng thức - Cực trị
Bài toán được giải quyết ở đây.
http://diendantoanho...dfracmc-na2ca2/
#341613 Topic bất đẳng thức THCS (2)
 Đã gửi bởi
le_hoang1995
on 29-07-2012 - 20:32
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 29-07-2012 - 20:32
trong
Bất đẳng thức và cực trị
$$VT=\sum \frac{a}{a+\sqrt{a+bc}}=\sum \frac{a}{a+\sqrt{a(a+b+c)+bc}}$$Bài 484:Cho $a,b,c\in R^{+}$ thỏa $a+b+c=1$.Chứng minh:
$$\frac{a}{a+\sqrt{a+bc}}+\frac{b}{b+\sqrt{b+ca}}+\frac{c}{c+\sqrt{c+ab}}\leq 1$$
$$=\sum \frac{a}{a+\sqrt{(a+b)(a+c)}}\leq \sum \frac{a}{a+\sqrt{ac}+\sqrt{ab}}$$
$$=\sum \frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1$$
#341457 ĐK để $x_1y_1+....+x_ny_n\geq (y_1+y_2+...+y_n)\sqrt[n]{x...
 Đã gửi bởi
le_hoang1995
on 29-07-2012 - 14:13
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
le_hoang1995
on 29-07-2012 - 14:13
trong
Bất đẳng thức - Cực trị
Mời mọi người cho ý kiến với điều kiện $x_1\geq x_2\geq ...\geq x_n>0;$
nếu $y_1\geq y_2\geq ...\geq y_n$ thì có xảy ra bất đẳng thức:
$x_1y_1+....+x_ny_n\geq (y_1+y_2+...+y_n)\sqrt[n]{x_1x_2..x_n}$
Dấu = xảy ra khi và chỉ khi $x_1=x_2=...=x_n$
Và khi dãy $y_1\leq y_2\leq ...\leq y_n$ bất đẳng thức đổi chiều
Với dãy y giảm thì có 1 cách là áp dụng trực tiếp BĐT chebusep và AM-GMĐể chứng minh bất đẳng thức trên có thể chứng minh bất đẳng thức sau: Với
$\alpha _1\geq \alpha _2\geq ...\geq \alpha _n>0;$
$ \alpha _1+\alpha _2+...+\alpha _n=1;$
Với $x_1\geq x_2\geq ...\geq x_n>0$
$x_1^{\alpha _1}.x_2^{\alpha _2}..x_n^{\alpha _n}\geq \sqrt[n]{x_1x_2...x_n}$.
Sau khi chứng minh được bất đẳng thức này tiếp tục áp dụng bất đẳng thức Chauchy suy rộng; từ đó ta có được dpcm
$$x_1y_1+x_2y_2+...+x_ny_n\geq \frac{1}{n}.(y_1+y_2+...+y_n)(x_1+...+x_n)$$
$$\geq \frac{1}{n}.(y_1+y_2+...+y_n).n\sqrt[n]{x_1x_2...x_n}=VP$$
Còn chiều ngược lại thì nếu làm như trên bị ngược dấu. Cái bđt trên kia chứng minh như thế nào anh?
#341118 ĐUỔI HÌNH BẮT CHỮ
 Đã gửi bởi
le_hoang1995
on 28-07-2012 - 15:53
trong
Góc giao lưu
Đã gửi bởi
le_hoang1995
on 28-07-2012 - 15:53
trong
Góc giao lưu




#341057 ĐUỔI HÌNH BẮT CHỮ
 Đã gửi bởi
le_hoang1995
on 28-07-2012 - 12:48
trong
Góc giao lưu
Đã gửi bởi
le_hoang1995
on 28-07-2012 - 12:48
trong
Góc giao lưu

#340941 Bạn ôn thi ở đâu?
 Đã gửi bởi
le_hoang1995
on 27-07-2012 - 23:01
trong
Góc giao lưu
Đã gửi bởi
le_hoang1995
on 27-07-2012 - 23:01
trong
Góc giao lưu
2. Mong sẽ có nhiều thầy cô và các bạn có thể hướng dẫn ôn thi đại học để các mem 95 đạt thành tích cao như các anh năm nay.
3. Em thấy riêng mem 95 thôi, vì vẫn có mục thi thử đại học cho tất cả mọi người mà.
4. Có ạ
Em xin cảm ơn BTC
#340701 $a+b+c=3$. Chứng minh bất đẳng thức : $$a^{\fra...
 Đã gửi bởi
le_hoang1995
on 27-07-2012 - 08:03
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
le_hoang1995
on 27-07-2012 - 08:03
trong
Bất đẳng thức - Cực trị
Cũng còn cách khác để chứng minh BĐT này.Ta sẽ chứng minh $(ab+bc+ca)(a^2b+b^2c+c^2a)\leq 9$
Không mất tổng quát, giả sử b nằm giữa a và c, ta có $$b^2c+c^2a=c(b-a)(b-c)+abc+bc^2\leq abc+bc^2$$.
$$\Rightarrow VT\leq b(a^2+ac+c^2)(ac+b(a+c))\leq \frac{b.[(a+c)^2+b(a+c)]^2}{4}=\frac{b.(a+c)^2.9}{4}$$
$$=9.b.\frac{a+c}{2}.\frac{a+c}{2}\leq 9.\left ( \frac{b+a+c}{3} \right )^3=9$$
#340324 CM: $\sqrt{6 +\sqrt{6+\sqrt{6+\sqrt...
 Đã gửi bởi
le_hoang1995
on 26-07-2012 - 07:33
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 26-07-2012 - 07:33
trong
Bất đẳng thức và cực trị
Bài 6. Cho a > 0, chứng minh rằng:
\[
\sqrt {a + \sqrt {a + ... + \sqrt a } } < \dfrac{{1 + \sqrt {4a + 1} }}{2}
\]
(ở vế trái có n dấu căn, n > 1)
Lời giải:
Đặt $$x_{1}=\sqrt{a},\; \; x_{2}=\sqrt{a+\sqrt{a}},\; \; ...,x_{n}=\sqrt{a+\sqrt{a+...+\sqrt{a}}}\; \; \; \left ( 1 \right )$$
Do $a>0$ nên ta có $x_{n}>x_{n-1}$. Từ (1) suy ra:
$$x_{n}^{2}=a+x_{n-1}\Rightarrow x_{n}^{2}<a+x_{n}\Rightarrow x_{n}^{2}-x_{n}-a<0\; \; \: \left ( 2 \right )$$
Xét tam thức bậc hai: $f\left ( t \right )=t^{2}-t-a$.
Từ (2) ta có $f\left ( x_{n} \right )<0$ nên theo định lí đảo về dấu tam thức bậc hai thì $t_{1}<x_{n}<t_{2}$ với $t_{1},\; t_{2}$ là hai nghiệm của $f\left ( t \right )$ tức:
$$x_{n}<\dfrac{1+\sqrt{4a+1}}{2}\; \; hay\; \; \sqrt{a+\sqrt{a+...+\sqrt{a}}}<\dfrac{1+\sqrt{4a+1}}{2}\; \; \; \; \;(đpcm)$$
Thay $a=6$ vào ta được $\sqrt{6+\sqrt{6+\sqrt{6+...}}}<3$
#339324 Topic bất đẳng thức THCS (2)
 Đã gửi bởi
le_hoang1995
on 23-07-2012 - 20:03
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 23-07-2012 - 20:03
trong
Bất đẳng thức và cực trị
Bổ sung thêm một cách nữa nhé, dạng của nó khiến ta nghĩ đến BĐT Chebusep.Mình làm bài này nếu đề là $\frac{3}{2\sqrt[3]{(abc)^2}}$
Áp dụng bất đẳng thức $Cauchy-Schwarz$ dạng $Engel$ và $AM-GM$ ta có:
$\frac{a}{bc(b+c)}+\frac{b}{ac(a+c)}+\frac{c}{ab(a+b)}=\frac{a^2}{abc(b+c)}+\frac{b^2}{abc(a+c)}+\frac{c^2}{abc(a+b)}\geq \frac{(a+b+c)^2}{2abc(a+b+c)}=\frac{a+b+c}{2abc}\geq \frac{3}{2\sqrt[3]{(abc)^2}}$
Không mất tổng quát, giả sử $ a \ge b \ge c$, khi đó cách bộ sau đơn điệu cùng chiều
$\left ( \frac{a}{b+c};\frac{b}{c+a};\frac{c}{a+b} \right )$ và $\left ( \frac{1}{bc};\frac{1}{ca};\frac{1}{ab} \right )$
Theo BĐT Chebusep và Nesbit
$$\frac{a}{bc(b+c)}+\frac{b}{ac(a+c)}+\frac{c}{ab(a+b)}\geq \frac{1}{3}.\left ( \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right ).\left ( \frac{1}{bc}+\frac{1}{ca}+\frac{1}{ab} \right )\geq \frac{1}{3}.\frac{3}{2}.\frac{3}{\sqrt[3]{(abc)^2}}=\frac{3}{2\sqrt[3]{(abc)^2}}$$
#339112 $ \frac{a}{b}+\frac{b}{c...
 Đã gửi bởi
le_hoang1995
on 23-07-2012 - 07:22
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 23-07-2012 - 07:22
trong
Bất đẳng thức và cực trị
PS, chết thật, làm ẩu quá, xin lỗi các bạn, mình làm lại.Bài toán:
Ch0 $a,b,c>0$,$a^2+b^2+c^2=3$
Chứng minh rằng:
$\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq \frac{9}{a+b+c}$
Ta chứng minh BĐT $$(a+b+c)\left ( \frac{a}{b}+\frac{b}{c}+\frac{c}{a} \right )\geq 3\sqrt{3(a^2+b^2+c^2)}$$.
Và do đó chỉ cần sử dụng BĐT trên với giả thiết $a^2+b^2+c^2=3$ là ra.
Có hai cách chứng minh BĐT này
$$
$$Theo BĐT Cauchy-schwarz ta có
$$VT\geq \frac{(a+b+c)^3}{ab+bc+ca}$$
Như vậy ta cần chứng minh
$$(a+b+c)^3\geq 3(ab+bc+ca)\sqrt{3(a^2+b^2+c^2)}$$
$$\Leftrightarrow (a+b+c)^3\geq 3\sqrt{3(a^2+b^2+c^2)(ab+bc+ca)^2}$$
Theo BĐT AM-GM ta có
$$3\sqrt{3(a^2+b^2+c^2)(ab+bc+ca)^2}\leq 3\sqrt{3.\left ( \frac{a^2+b^2+c^2+2(ab+bc+ca)}{3} \right )^3}=(a+b+c)^3$$
ĐPCM
Cách 2.
Nhân ra ta phải chứng minh $$\sum \frac{ab}{c}+\sum \frac{a^2}{b}+\sum a\geq 3\sqrt{3(a^2+b^2+c^2)}$$
Sử dụng BĐT $ (x+y+z)^2 \geq 3(xy+yz+zx)$ ta được
$$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\geq \sqrt{3(b^2+c^2+a^2)}$$
Như vậy ta cần chứng minh $$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+a+b+c\geq 2\sqrt{3(a^2+b^2+c^2)}$$
Ta sẽ chứng minh BĐT mạnh hơn là $$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+a+b+c\geq\frac{6(a^2+b^2+c^2)}{a+b+c}$$
Không mất tổng quát, giả sử b là số nằm giữa a và c. BĐT cần chứng minh tương đương với
$$\sum \left ( \frac{a^2}{b}-2a+b \right )\geq \frac{6(a^2+b^2+c^2)}{a+b+c}-2(a+b+c)$$
$$\Leftrightarrow \sum \frac{(a-b)^2}{b}\geq \frac{6(a^2+b^2+c^2)}{a+b+c}-2(a+b+c)$$
Theo cauchy-schwarz ta có $$\sum \frac{(a-b)^2}{b}\geq \frac{4(a-c)^2}{a+b+c}$$
Như vậy cần phải chứng minh $$2(a-c)^2\geq 3(a^2+b^2+c^2)-(a+b+c)^2\Leftrightarrow (b-c)(b-a)\leq 0$$
Đúng theo giả sử. Vậy BĐT trên đúng. Mặt khác dễ thấy $$\frac{6(a^2+c^2+c^2)}{a+b+c}\geq 2\sqrt{3(a^2+b^2+c^2)}\Leftrightarrow \sqrt{3(a^2+b^2+c^2)}\geq a+b+c$$
Đúng nên ta suy ra ĐPCM
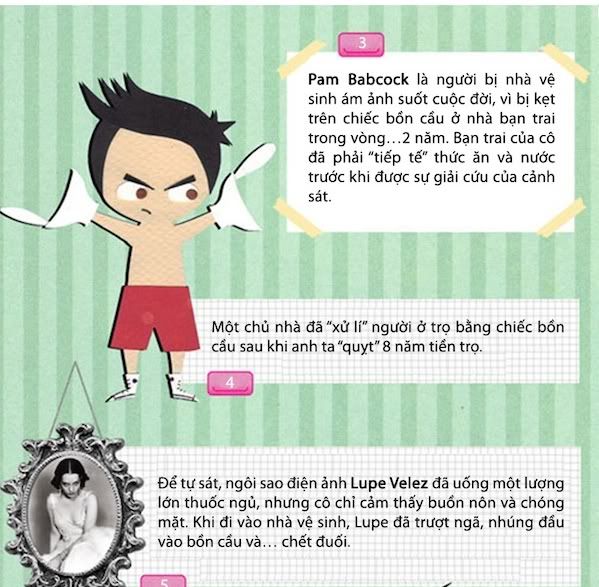
#338396 Toilet thú vị
 Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:46
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:46
trong
Quán hài hước
#338393 Toilet thú vị
 Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:38
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:38
trong
Quán hài hước
Bạn có muốn thử không?
Chắc hẳn các bạn vẫn còn nhớ đến nhà hàng toilet tại Trung Quốc. Mới đây, một nhà hàng tương tự đã được khai trương tại Thủ đô Bắc Kinh của Trung Quốc. Nhà hàng tiếp tục gây sốc cho nhiều người với hình thức phục vụ thức ăn kiểu… nhà vệ sinh.

Nhà hàng toilet ở Trung Quốc.
Bạn có muốn ăn?
[font='normal Arial', ', Helvetica, sans-serif} ']Nhà hàng được thiết kế như một nhà vệ sinh công cộng. Những món ăn ngon miệng và hấp dẫn sẽ được đựng trong các bồn cầu thu nhỏ rồi mang lên phục vụ thực khách. Một số khách hàng tỏ ra thích thú với hình thức độc đáo này, tuy nhiên nhiều người lại thấy nó rất kinh khủng…[/font]
[font=normal Arial', Helvetica, sans-serif]
Thức ăn được đựng trong các bồn cầu thu nhỏ.
 [/font]
[/font]
Nguồn: http://www.vietgiait...n-tai-bac-kinh/
#338391 Toilet thú vị
 Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:32
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:32
trong
Quán hài hước
Và những bật mí kinh ngạc về cách sử dụng toilet cùng giấy toilet trên toàn thế giới!

#338384 Toilet thú vị
 Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:18
trong
Quán hài hước
Đã gửi bởi
le_hoang1995
on 21-07-2012 - 13:18
trong
Quán hài hước

#336698 $(a^{2}+1)(b^{2}+1)(c^{2}+1)\geq (ab+...
 Đã gửi bởi
le_hoang1995
on 17-07-2012 - 08:03
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 17-07-2012 - 08:03
trong
Bất đẳng thức và cực trị
1 phát bài 405:
Biến đổi tương đương,ta có:
BĐT cần chứng minh tương đương $(a+b+c)^2+a^2b^2c^2\geq 2abc(a+b+c)<=>(a+b+c-abc)^2\geq 0$
BĐT sau cùng đúng nên có đpcm
Có mấy hum không lên mà topic nì sôi động qá
Cách khác cho bài này :
$VT=[(a+b)^{2}+(ab-1)^{2}](c^{2}+1)\geq [c(a+b)+ab-1]^{2}= (ab+bc+ca-1)^{2}$
Xong !
#336682 $\frac{a}{b+2c+3a}+\frac{b}...
 Đã gửi bởi
le_hoang1995
on 17-07-2012 - 00:42
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 17-07-2012 - 00:42
trong
Bất đẳng thức và cực trị
Một cách trâu bò, quy đồng lên, ta phải chứng minhCho a,b,c$> 0$
chứng minh $\frac{a}{b+2c+3a}+\frac{b}{c+2a+3b}+\frac{c}{a+2b+3c}\leq \frac{1}{2}$
$$2(a^3+b^3+c^3)+3(a^2b+b^2c+c^2a)\geq 12abc+(ab^2+bc^2+ca^2)$$.
Nhưng đây là tổng của 2 BĐT quen thuộc dùng Schur và AM-GM.
$$a^3+b^3+c^3+3abc\geq (a^2b+b^2c+c^2a)+(ab^2+bc^2+ca^2)$$
$$(a^3+b^3+c^3)+4(a^2b+b^2c+c^2a)\geq 3abc+12abc=15abc$$
Dấu bằng xảy ra khi $a=b=c$
#336680 Cho $3^{-x}+3^{-y}+3^{-z}=1$
 Đã gửi bởi
le_hoang1995
on 17-07-2012 - 00:28
trong
Bất đẳng thức và cực trị
Đã gửi bởi
le_hoang1995
on 17-07-2012 - 00:28
trong
Bất đẳng thức và cực trị
Đặt $3^x=a;3^y=b;3^z=c$, ta quy bài toán vềChứng minh: $\frac{9^{x}}{3^{x}+3^{y}3^{z}}+\frac{9^{y}}{3^{y}+3^{x}3^{z}}+\frac{9^{z}}{3^{z}+3^{y}3^{x}}\geq \frac{3^{x}+3^{y}+3^{z}}{4}$
Cho $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1\Leftrightarrow ab+bc+ca=abc$, chứng minh rằng
$$\frac{a^2}{a+bc}+\frac{b^2}{b+ca}+\frac{c^2}{c+ab}\geq \frac{a+b+c}{4}$$.
Ta chứng minh như sau.
$$VT=\sum \frac{a^2}{a+bc}=\sum \frac{a^3}{a^2+abc}=\sum \frac{a^3}{a^2+ab+bc+ca}=\sum \frac{a^3}{(a+b)(a+c)}$$.
Ta cần chứng minh $\frac{a^3}{(a+b)(a+c)}+\frac{b^3}{(b+c)(b+a)}+\frac{c^3}{(c+a)(c+b)}\geq \frac{a+b+c}{4}$
Có nhiều cách chứng minh bài này, ở đây mình làm theo cách Holder, có thể làm theo AM-GM cũng được.
$$VT\geq \frac{(a+b+c)^3}{[(a+b)+(b+c)+(c+a)].[(a+c)+(b+a)+(c+b)]}=\frac{(a+b+c)^3}{4(a+b+c)^2}=VP$$
ĐPCM
- Diễn đàn Toán học
- → le_hoang1995 nội dung