Cho m,n là 2 số nguyên dương và $m|n$. Tìm ideal A của $\mathbb{Z}_n$ sao cho $\mathbb{Z}_n/A\cong \mathbb{Z}_m$.

CMR: nếu $u=u(x,t)$ thoả phương trình truyền nhiệt $\frac{\partial u }{\partial t}=a^2\frac{\partial^2 u}{\partial x^2}, a>0$ thì

$v=\frac{1}{a\sqrt{t}}e^{-\frac{x^2}{4a^2t}}u(\frac{x}{a^2t},\frac{-1}{a^4t}), t>0$ cũng thoả phương trình đó.

Chứng minh rằng: Nhóm $\mathbb{Q}/\mathbb{Z}$ có cấp vô hạn nhưng mọi phần tử có cấp hữu hạn.

Không biết có nhầm gì không chứ $G$ đâu chứa nhóm con cấp $p^d$ với $d>k$ nhỉ, vì $|K|=p^d|p^km=|G|\Rightarrow p^d|p^k\Rightarrow d\leq k$ (vì $(p,m)=1$). Chắc đề là $0<d\leq k$ (mà chắc cũng không cần vì tự suy ra được từ 2 cái màu xanh).
Ta có $H\cap K$ là nhóm con của $K$ mà $K$ không là nhóm con của $H$ nên $H\cap K\neq K$, nên $|H\cap K|=p^e,e<d$. Theo công thức này, $|HK|=\frac{|H||K|}{|H\cap K|}=\frac{p^{k+d}}{p^e}=p^{k+d-e}$, ta có $k+d-e>k$, theo suy luận ở trên thì $HK$ không thể là nhóm con của $G$ (vì $|HK|=p^{k+d-e}\nmid p^km=|G|$).

bạn có cách nào để chứng minh cái công thức màu xanh ko á?

Cho $G$ là nhóm cấp $p^km$, với $p$ là số nguyên tố  và $(p, m)=1$. Giả sử $H$ là nhóm con cấp $p^k$ và K là nhóm con cấp $p^d$, $0<k\leq d$  nhưng $K$ không là nhóm con của $H$. CMR:          

$HK$ không là nhóm con của G.

Với $S\subset G,g\in G$, ký hiệu $S^{-1}=\{s^{-1}|s\in S\},gS=\{gs|s\in S\}$.
Lưu ý $x^{-1}=y^{-1}\Leftrightarrow x=y, gx=gy\Leftrightarrow x=y,\forall x,y,g\in G$, vậy nên $|S|=|S^{-1}|,|S|=|gS|,\forall S\subset G,g\in G$.
Lấy $g\in G$ bất kì, ta có $|H|+|gK^{-1}|=|H|+|K|>|G|$ nên $|H\cap gK^{-1}|>0$, chọn được $h\in H\cap gK^{-1},k\in K,gk^{-1}=h$ thì $hk=g$, vậy $G=HK$. 

Bạn giải thích cái chỗ mà $\left | H \right |+\left | gK^{-1} \right |>|G|$ thì có đc $|H\cap gK^{-1}|>0$ giúp mình với ạ.

Cho $G$ là một nhóm hữu hạn và $H, K \subset G$. CMR

$\left | H \right |+ \left | K \right |>\left | G \right | \Rightarrow G=HK=\left \{ ab/ a\in H,b \in K \right \}$

Cho dãy số Fibonacci $\left\{\begin{matrix} F_1=F_2=1 & \\ F_n=F_{n-1}+F_{n-2} & \end{matrix}\right.$ Chứng minh rằng: $F_m |F_n \Leftrightarrow m|n$

Bài 1: Cho$p$ là số nguyên tố. CMR:

a) $C^{k}_{p}\equiv 0 (mod p)$ $\forall k=\overline{1,p-1}$

b)$C^{k}_{p-1}\equiv (-1)^{k} (modp)$ $\forall k=\overline{1,p-1}$

Bài 2: Cho Cho dãy số Fibonacci $\left\{\begin{matrix} F_1=F_2=1 & \\ F_n=F_{n-1}+F_{n-2} (n\geqslant 3) & \end{matrix}\right.$. Chứng minh $(m,n)=d \Rightarrow (F_m,F_n)=F_d$

Bài 3: Cho $p$ là số nguyên tố và $a$ là sô nguyen dương nhỏ hơn $p$. CMR pt $ax\equiv b(modp)$ có nghiệm là:

$x\equiv b(-1)^{a-1}.\frac{(p-1)(p-2)...(p-a+1)}{a!}(modp)$

Bài 4: Cho $\sigma (n)=\sum_{d|n}d$. Số tự nhiên $n\in \mathbb{N}^{*}$ là số thiếu nếu $\sigma (n)<2n$, số thừa nếu $\sigma (n)>2n$. CMR

a) Có vô số số tự nhiên thỏa $\sigma (n)=2n-1$

b) Số lẻ chỉ có 2 ước nguyên tố cùng nhau là sô thiếu.

Cho tứ diện $ABCD$ có thể tích bằng $3$. Trên các mật phẳng $(BCD), (ACD), (ABD), (ABC)$ lần lượt lấy các điểm $A_{1}, B_{1}, C_{1}, D_{1}$ sao cho $AA_1// BB_1// CC_1// DD_1$. Tính thể tích khối tứ diện $A_1B_1C_1D_1$.

Cho ma trận $A=(a_{ij})_{n\times n}$

Tính det(A) với $a_{ij}=|i-j|$?

1) Từ giả thiết $\Leftrightarrow 3z^2-6xy.z+x^2+2y^2=0(*)$

Ta xem (*) là pt bậc 2 theo ẩn z với x,y là tham số.

(*) có nghiệm $\Leftrightarrow \Delta'_{(*)}\geq 0 \Leftrightarrow (3xy)^2-3(x^2+2y^2)\geq 0 \Leftrightarrow \frac{1}{y^2}+\frac{2}{x^2}\leq 3.$ $(**)$

Từ $(**)\Rightarrow 9\geq (1+2)(\frac{1}{y^2}+\frac{2}{x^2})=(1^2+(\sqrt{2})^2)(\frac{1^2}{y^2}+\frac{(\sqrt{2})^2}{x^{2}})\geq (\frac{1}{x}+\frac{2}{y})^2$ (Bunhiacopxki)

$\Rightarrow \frac{1}{y}+\frac{2}{x}\leq 3.\square$.

Dấu "=" $\Leftrightarrow \frac{1}{1/y}=\frac{\sqrt{2}}{\sqrt{2}/x} \Rightarrow x=y=z=1$.

TXĐ: $\ D=\mathbb{R} \Rightarrow f(x)$  liên tục trên $\ \mathbb{R}$ 

$\ f'(x)=x^4+(m-6)x^3-3(2m+1)x^2+18x=x(x-6)(x^2+mx-3)$

$\ f'(x)=0 \Leftrightarrow x=0 \vee x=6\vee x=\frac{-m\pm \sqrt{m^2+12}}{2}$

Nhận xét: $\ \left\{\begin{matrix}-m+\sqrt{m^2+12}>0 & \\ -m-\sqrt{m^2+12}<0 & \end{matrix}\right. , \forall m$

Gọi $\ x_1,x_2,x_3,x_4$ là no của $\ f'(x)=0$ và không mất tính tổng quát của bài toán, ta giả sử $\ x_1< x_2< x_3$

Ycbt $\ \Leftrightarrow \left | x_1-x_2 \right |+\left |x_3-x_4 \right |=2 \Leftrightarrow \left | \frac{-m-\sqrt{m^2+12}}{2}-0 \right |+\left | \frac{-m+\sqrt{m^2+12}}{2}-6 \right |=2 \Leftrightarrow m+\sqrt{m^2+12}+\left | \sqrt{m^2+12}-m-12 \right |=4 (*)$

$\ TH1: \sqrt{m^2+12}-m-12>0 \Rightarrow (*)\Leftrightarrow m+\sqrt{m^2+12}+\sqrt{m^2+12}-m-12=4 \Leftrightarrow ...\Leftrightarrow m=\pm 2\sqrt{13}$

So đk, ta nhận $\ m=-2\sqrt{13}$

$\ TH2:\sqrt{m^2+12}-m-12<0 \Rightarrow (*) \Leftrightarrow m+\sqrt{m^2+12}-\sqrt{m^2+12}+m+12=4\Leftrightarrow m=-4$

So đk, ta nhận $\ m=-4$

Vậy $\ m\in \left \{ -4; -2\sqrt{13} \right \}$ thì thỏa ycbt.

Câu 4:

Chọn $\ a \in X\setminus \left \{ 0 \right \}: 20$ cách

       $\ b\in X: 21$ cách 

         $\ c \in X: 21$ cách 

=> KGM: $\ n(\Omega )=20.21.21=8820$

$\ * y=\frac{a}{3}x^3-bx^2+cx\Rightarrow y'=ax^2-2bx+c$

Hàm số cho đạt cực trị tại $\ x=1$ 

$\ \Leftrightarrow \left\{\begin{matrix} a\neq 0 & & \\ \Delta_{y'}>0 & & \\ y'(1)=0 & & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a\neq 0 & & \\ b^2-ac>0 & & \\ a-2b+c=0 & & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a\neq 0 & & \\ (a+c)^2-4ac>0 & & \\ a+c=2b & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} a\neq 0 & & \\ a\neq c & & \\ a+c=2b & & \end{matrix}\right.$

=> Ta cần chọn các số $\ a, b, c$ ($\ a \neq c$) sao cho $\ a, b, c$ lạp thành CSC

Ta có: $\ b\in \mathbb{Z} \Rightarrow $ 2b chẵn => a+c chẵn => 2 số a, c phải cũng chẵn hoặc cùng lẻ.

TH1: a,c cùng lẻ

Chọn a: 10 cách          

    $\ c \neq a: 9$ cách  

=> có $\ 10.9=90$ cách 

TH2: a,c cùng chẵn 

Chọn $\ a \neq 0: 10$ cách

      $\ c \neq a: 10$ cách

=> có $\ 10.10=100$ cách 

=> có tất cả $\ 100+90=190$ hàm số thỏa ycbt.

Vậy xác xuát cần tìm là: $\ P=\frac{190}{8820}=\frac{19}{882}$.

P/s: ở đây mình  chỉ càn chọn 2 số a,c vì từ pt a+c=2b ta có đc tính chát của a,c, đòng thời từ a,c ta sẽ có dc b.

$\ a,c\in \left [ -10;10 \right ] \Rightarrow a+c\in \left [ -20;20 \right ]\Rightarrow 2b\in \left [ -20;20 \right ] \Rightarrow b\in \left [ -10;10 \right ]$   

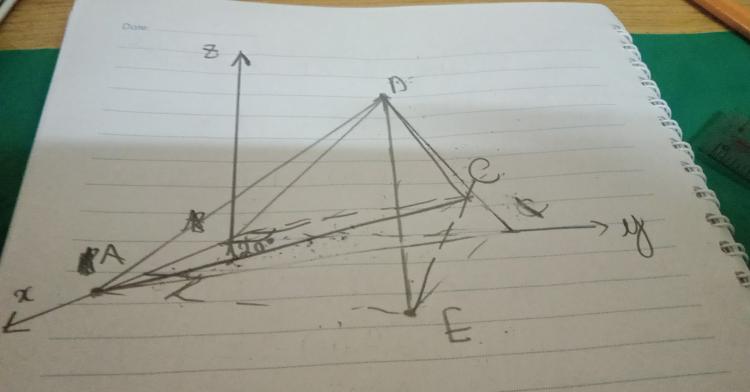
Câu 3b: (xem hình vẽ)

Gọi $\ R$ là bán kính mặt cầu ngoại tiếp tứ diện $\ ABCD$

Chọn hệ tọa độ $\ Oxyz$ sao cho:

$\ A(a;0;0), B(0;0;0), C(2a\cos 120^o;2a\sin 120^o;0)=C(-a;a\sqrt{3};0)$

* Cần tìm D <= phải tìm E.

Xét mp $\ Oxy$

Ta có $\ EA\perp AB(cmt)$ $\ \Rightarrow x_E=a$

Mà $\ \widehat{EBA}=30^o => BE: y-0=\tan 30^o(x-0) \Leftrightarrow BE:y=\frac{\sqrt{3}}{3}x \Rightarrow E(a;\frac{a\sqrt{3}}{3};0)$

Lại có: $\ \left\{\begin{matrix} DE\perp (ABC) & \\ DE=\frac{a}{\sqrt{6}} & \end{matrix}\right. \Rightarrow D(a;\frac{a\sqrt{3}}{3};\frac{a}{\sqrt{6}})$

Gọi $\ (S): x^2+y^2+z^2-2Ax-2By-2Cz+D=0$ là phương trinh mặt cầu ngoại tiếp tứ diện $\ ABCD$

$\ B(0;0;0)\in (S) =>D=0$

$\ A(a;0;0)\in (S) => A=\frac{a}{2}.$

$\ C(-a;a\sqrt{3};0)\in (S) \Rightarrow B=\frac{5a}{2\sqrt{3}}$

$\ D(a;\frac{a\sqrt{3}}{3};\frac{a}{\sqrt{6}})\in (S) \Rightarrow C=\frac{-7\sqrt{6}a}{12}$

Vậy $\ R=\sqrt{A^2+B^2+C^2-D}=a\sqrt{\frac{35}{8}}$

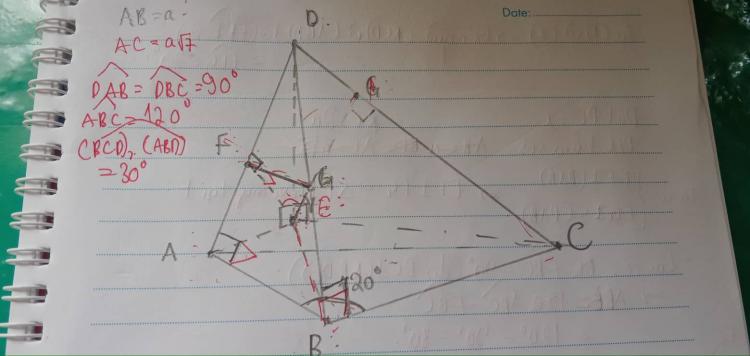
Câu 3a: TT (xem hình vẽ)

Kẻ $\ DE\perp (ABC)$ tại $\ E$

Gọi F, G lần lượt là hình chiếu của E lên DA và DB.

$\ \left\{\begin{matrix}AB\perp AD & \\ AB\perp DE \ & \end{matrix}\right. \Rightarrow AB\perp (ADE)$

Mà $\ EF\subset (ADE) \Rightarrow AB\perp EF$

Lại có $\ AD\perp EF$

$\ \Rightarrow EF\perp (ABD) (1)$

$\ \left\{\begin{matrix} BC\perp DE & \\ BC\perp DB & \end{matrix}\right. \Rightarrow BC\perp (BDE) \Rightarrow BC \perp EG (EG\subset (BDE))$

Mà $\ BD\perp EG \Rightarrow EG\perp (BCD)(2)$

Từ (1) và (2) => Góc giữa $\ (BCD)$ và $\ (ABD)$ là $\ \widehat({EF,EG})=\widehat{FEG}=30^{o}$

Đặt $\ DE=x$

Đ/l hàm cos: $\ BC=2a$

Ta có: $\ \left\{\begin{matrix} EF\perp (DAB) & \\ FG\subset (DAB) & \end{matrix}\right. => EF\perp FG \Rightarrow \Delta EFG$ vuông tại F.

Lại có $\ \widehat{EBC}=90^{o}(BC\perp (BDE))$

$\ \Rightarrow \widehat{ABE}=\widehat{ABC}-\widehat{EBC}=120^{o}-90^{o}=30^{o}$

$\ \Delta ABE$ vuông tại A:

$\ \tan 30^{o}=\frac{EA}{AB}\Rightarrow EA=\frac{a\sqrt{3}}{3}$

$\ EB=\sqrt{EA^2+AB^2}=\frac{2a\sqrt{3}}{3}$

$\ \Delta AED$ vuông tại E có đg cao EF

$\ \frac{1}{EF^2}=\frac{1}{ED^2}+\frac{1}{EA^2}\Rightarrow EF=\frac{a\sqrt{3}{x}}{3\sqrt{(\frac{a\sqrt{3}}{3})^2+x^2}}$

$\ \Delta EBD$ vuông tại E có đg cao EG

$\ \frac{1}{EG^2}=\frac{1}{ED^2}+\frac{1}{EB^2}\Rightarrow EG=\frac{2a\sqrt{3}x}{3\sqrt{(\frac{2a\sqrt{3}}{3})^2+x^2}}$

$\ \Delta EFG$ vuông tại F có $\ \widehat{FEG}=30^o$

$\ \cos 30^o=\frac{EF}{EG} \Leftrightarrow \frac{\sqrt{3}}{2}=\frac{1}{2}.\frac{\sqrt{\frac{4a^2}{3}+x^2}}{\sqrt{\frac{a^2}{3}+x^2}} \Leftrightarrow ...\Rightarrow x=\frac{a}{\sqrt{6}}$

Vậy $\ V_{ABCD}=\frac{1}{3}.DE.S_{\Delta ABC}=\frac{1}{3}.\frac{a}{\sqrt{6}}.\frac{1}{2}a.2a.\sin 120^o=\frac{a^3}{6\sqrt{2}}$

Câu 2: độc giả tự giải vì không quá khó. Sử dụng công thức đạo hàm và pttt là ra.

DS: y=202x+2020.

Câu 1: Phân tích

Đầu tiên, ta dùng pp Hàm đăc trưng do không thể biến đổi thông thuòng theo cách đại số.

  Tiếp theo, ta tách các logarit bà chuyển về mỗi vế.

   $\log_{3}(x+5)^{2} + (...) = \log_{3}(x+1)^2+ (...)$

Như vậy là đã xong, nhưng cái khó khăn ở đây là bài này giấu rất kĩ, biến đổi $x^2+x$ sang biểu thức bao gồm $(x+5)^2$ và $(x+1)^2$. Do đó, từ ý tưởng và câu hỏi tự đặt ra. Mình có phương pháp sau:

Ta cần biểu diễn $x^2 +x$ theo $(x+5)^2$ và $(x+1)^2$, tức là:

 $ x^{2}+ x=a(x^{2}+10x+25)+b(x^{2}+2x+1)+c$

$ \Leftrightarrow x^{2}+x=(a+b)x^2+(10a+2b)x +25a+b+c$

$ \Rightarrow \left\{\begin{matrix} a+b=1 & & \\ 10a +2b=1 & & \\ 25a+b+c=0 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} a=-\frac{1}{8} & & \\ b=\frac{9}{8} & & \\ c=2 & & \end{matrix}\right.$ 

Giải

 ĐK: $\ \left\{\begin{matrix} x\neq -5 & \\ x\neq -1 & \end{matrix}\right.$ 

PT $ \Leftrightarrow \log _{3}(x+5)^2-\log _{3}(x+1)^2=-\frac{1}{8}(x^2+10x+25)+\frac{9}{8}(x^2+2x+1)+2$

$ \Leftrightarrow \log _{3}(x^2+10x+25)+\frac{1}{8}(x^2+10x+25)=\log _{3}(9x^2+18x+9)+\frac{1}{8}(9x^2+18x+9)$

Xét hàm số $ f(t)=\log_{3}t+\frac{1}{8}t, t\in (0;+\infty )$

$ f'(t)=\frac{1}{t\ln3}+\frac{1}{8}>0, \forall t\in (0;+\infty )$

$ \Rightarrow f(t)$ đồng biến trên $\ (0;+\infty )$

$ \Rightarrow f(x^2+10x+25)=f(9x^2+18x+9)$

$\ \Leftrightarrow x^2+10x+25=9x^2+18x+9$

$\ \Leftrightarrow 8x^2+8x-16=0$

$\ \Leftrightarrow x=-2 \vee x=1$ (nhận)

 Vậy $ S=\left \{ -2;1 \right \}$

SỞ GD&ĐT TP.HỒ CHÍ MINH

KÌ THI HSG CẤP THÀNH PHỐ

Khóa ngày: 07/04/2022

Thời gian làm bài: 120 phút (không kể thời gian phát đề)

Câu 1: (3 điểm)
Giải phương trình: $ \log_3\left(\frac{x+5}{x+1}\right)^2=x^2+x$.

Câu 2: (3 điểm)