Chủ đề dài, gồm 5 phần.
- Mở đầu
- Dựng hình dưới góc nhìn của Đại số
- Một chút đại số trừu tượng
- Chứng minh của Edmund Landau
- Lời kết
(Xuyên suốt bài viết này, chúng ta quy ước: dựng hình là dựng hình bằng thước thẳng và compass)
1. Mở đầu
Các bài toán dựng hình đã được nghiên cứu từ thời Hy Lạp cổ đại. Trong giai đoạn đó, nổi lên ba bài toán dựng hình sau:
- Chia một góc cho trước thành ba góc bằng nhau.
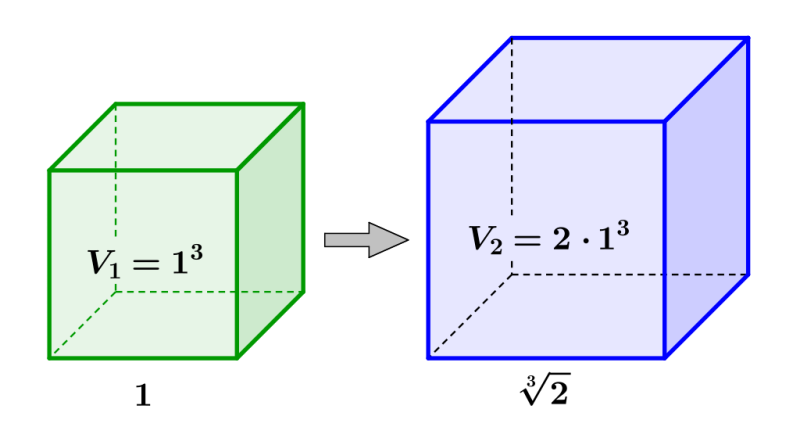
- Dựng một hình lập phương có thể tích gấp đôi thể tích một hình lập phương cho trước.
- Dựng một hình vuông có diện tích bằng một đường tròn cho trước.
Với những ai đọc về lịch sử toán học, hẳn mọi người đã biết tới ba bài toán dựng hình này, cũng như biết rằng câu trả lời cho cả ba bài toán là: không dựng được. Hai bài toán đầu tiên được giải quyết sau khoảng 2000 năm, bởi nhà toán học người Pháp Pierre Wantzel, bằng đại số, trong đó có lý thuyết mở rộng trường (Theory of Field Extensions).
Trong bài viết này, mình trình bày chứng minh cho bài toán dựng hình thứ hai trong danh sách trên. Tuy nhiên, mình không trình bày chứng minh của Pierre Wantzel, mà là của Edmund Landau. Lý do là mới đây, khi đọc Chương 6 trong cuốn Mathematics and Its History (3rd edition, written by John Stillwell), mình đã được thấy ý tưởng của chứng minh đó (ít nhất là với mình) của Landau. Vì mừng quá, nên mình bắt tay vào viết một chủ đề ngắn nhằm trình bày chứng minh đó theo cách tiếp cận được, sao cho các bạn học sinh trung học phổ thông cũng có thể hiểu và appreciate (các bạn học sinh trung học phổ thông nếu có biết các kiến thức này rồi thì mong các bạn lượng thứ, vì mình không biết hiện nay các bạn học sinh nói chung và học sinh ôn thi học sinh giỏi, Olympic học gì đâu). Trong quá trình viết, mình cũng vỡ lẽ hơn.
Đính chính: Chứng minh trong bài viết này được truyền cảm hứng từ ý tưởng chứng minh của Landau được nêu trong cuốn sách Mathematics and Its History. Mình chỉ triển khai chứng minh đó và bổ sung những gì mình thấy là chưa thuyết phục. Mình chưa tìm ra chứng minh nguyên bản của Landau.
Spoiler alert: Chứng minh vẫn sử dụng các kiến thức toán học ngoài chương trình phổ thông từ lớp 1 đến 12 của Việt Nam hiện nay (Thời điểm bài viết này bắt đầu được soạn lằ ngày 6 tháng 7 năm 2023). Tuy nhiên, hàm lượng các kiến thức đó trong chứng minh của Landau là không nhiều, và có thể diễn đạt đi vào lòng học sinh phổ thông Việt Nam được. Phần chính của bài viết là mục 4. Các mục trước đó tồn tại nhằm mục đích giới thiệu và chuẩn bị kiến thức.
Những điều cần có để đọc bài viết:
- Internet và sự kiên nhẫn.
- Hệ tọa độ Descartes, phương trình đường thẳng và đường tròn.
- Căn thức và cách giải phương trình bậc hai.
Mong rằng, ngay cả với các bạn đọc dù đã có những kiến thức đáng kể về đại số cũng có thể đọc chủ đề này mà không cảm thấy khó chịu về mặt Toán học, và xem đây như một cuộc dạo chơi nhẹ nhàng.
Nếu có sơ suất trong bài viết này, mong bạn đọc chỉ giáo, đặt câu hỏi.
2. Dựng hình dưới góc nhìn của Đại số
2.1. Nhắc lại về dựng hình
Dựng hình bằng thước và compass là một công việc có phần trừu tượng. Dựng hình chỉ cung cấp hai dụng cụ vẽ hình là cây thước thẳng dài vô hạn không chia độ dài (để vẽ đường thẳng đi qua hai điểm phân biệt), và compass có khẩu độ tùy ý (để vẽ đường tròn với tâm cho trước và đi qua một điểm cho trước khác). Rõ ràng đây đều là những công cụ không có thật, nhưng lại lý tưởng vì chúng ta có thể vẽ một đoạn thẳng dài tùy ý, một đường tròn với bán kính tùy ý.
Vậy dựng hình thì làm gì? Là việc dựng những đối tượng hình học (điểm, đoạn thẳng, đường tròn) bằng hai công cụ trên, khi đã cho sẵn một số đối tượng hình học khác.
Chỉ còn lại câu hỏi là làm như thế nào. Câu trả lời của mình là
- Áp dụng những phép dựng nền tảng (dựng đường thẳng đi qua hai điểm phân biệt, dựng đường tròn với tâm cho trước và đi qua một điểm cho trước khác, dựng giao điểm của hai đường thẳng phân biệt và không song song, dựng giao điểm đường thẳng và đường tròn, dựng giao điểm hai đường tròn).
- Áp dụng các tiên đề, định lý hình học. Tức là với tiên đề, định lý này, chúng ta luận ra được rằng có thể dựng được đối tượng này khi đã có trước những đối tượng kia. Ví dụ, để dựng tâm đường tròn ngoại tiếp của một tam giác cho trước, chúng ta dùng tới phép dựng đường trung trực, và định lý rằng ba đường trung trực của một tam giác đồng quy tại tâm đường tròn ngoại tiếp.
Tóm lại, câu chuyện vẫn là quy về những gì đã biết, và chia nhỏ đến mức độ tiên đề và các phép dựng nền tảng.
(Nếu bạn hỏi tại sao lại dựng hình, thì có lẽ bài viết này không dành cho bạn, và mình cũng không trả lời được tại sao).
Dựng hình đã được giới thiệu từ chương trình trung học cơ sở. Tính đến năm mà mình học trung học cơ sở (năm 2009), đã có quyết định giảm tải nội dung này. Tuy vậy, mình tin là bạn đọc nào đã học qua toán ở bậc trung học cơ sở đều đã được học qua những phép dựng hình sau, hoặc biết tới những định lý gắn với các phép dựng này:
- Cho trước một đoạn thẳng, dựng đường trung trực của đoạn thẳng đó.
- Cho trước một góc, dựng đường phân giác trong của góc đó.
- Cho trước một đường thẳng và một điểm nằm ngoài đường thẳng. Qua điểm đó, hãy dựng đường thẳng đi qua điểm đó và song song với đường thẳng cho trước.
- Dựng tam giác đều (ở đây, đối tượng cho trước có thể là một đường tròn, hay là hai điểm phân biệt, ...)
- Cho trước một tam giác, dựng đường tròn đi qua ba đỉnh của tam giác đó.
- Cho trước một tam giác, dựng các đường tròn tiếp xúc với ba cạnh của tam giác đó.
2.2. Hệ tọa độ Descartes
Hình học và số học là hai nhánh Toán học cổ xưa nhất. Các ý tưởng đại số cũng đã manh nha, theo cùng hình học gần như từ đầu. Chỉ có điều ở thuở sơ khai, ý tưởng và diễn đạt cho đại số còn gắn chặt với Hình học (chẳng hạn, tính chất phân phối của phép nhân với phép cộng được diễn đạt bằng tổng diện tích của các hình chữ nhật xếp sát nhau, trong Mệnh đề 1, Quyển 2 của bộ Elements viết bởi Euclid). Chỉ từ thời kỳ Phục Hưng trở đi, các nhà toán học mới dùng kí hiệu để làm các phép toán, và đại số được giải phóng khỏi Hình học. Nhưng rồi đại số cũng quay trở lại để hỗ trợ hình học dưới dạng hệ tọa độ Descartes.
Với hệ tọa độ Descartes, ta có thể tương ứng mặt phẳng với hệ tọa độ Descartes Oxy (hai trục), tương ứng các đường (chẳng hạn đường thẳng, đường tròn và các đường conic khác...) với một phương trình. Bằng cách đó, các bài toán hình học được quy về bài toán đại số, dù chưa chắc đã giải được. Các bài toán dựng hình cũng không phải ngoại lệ. Mục ngay sau đây dùng để giới thiệu đoạn từ điển hình học/dựng hình - hệ tọa độ Descartes.
2.3. Dựng hình dưới góc nhìn của đại số
Chúng ta mang bài toán dựng hình sang hệ tọa độ Descartes. Để phương pháp đại số cho việc dựng hình được tiếp thu tốt và phát huy tác dụng, việc cần làm là thông dịch ngôn ngữ hình học sang đại số (ở đây là hệ tọa độ Descartes)
- Mặt phẳng ===> Tất cả các bộ hai số thực và có thứ tự $(x, y)$ (order pairs).
- Điểm ===> Một bộ hai số thực có thứ tự $(x, y)$.
- Đường thẳng ===> Phương trình $ax + by + c = 0$ (trong đó, $a$ và $b$ không đồng thời bằng không).
- Dựng đường thẳng đi qua hai điểm cho trước ===> Đưa ra phương trình dạng $ax + by + c = 0$ sao cho hai bộ (ứng với hai điểm) $(x_{1}, y_{1})$ và $(x_{2}, y_{2})$ thỏa mãn phương trình đó.
- Đường tròn ===> Phương trình ${(x - a)}^{2} + {(y - b)}^{2} = {r}^{2}$ (trong đó, $(a, b)$ là tâm đường tròn, còn $r$ là bán kính đường tròn).
- Dựng đường tròn với tâm là một điểm cho trước, đi qua một điểm cho trước khác ===> Đưa ra phương trình dạng ${(x - a)}^{2} + {(y - b)}^{2} = {r}^{2}$, trong đó $(a, b)$ tương ứng với tâm đường tròn, còn $r$ là khoảng cách giữa hai điểm cho trước.
- Giao điểm của hai đường ===> Nghiệm của một hệ phương trình (mỗi phương trình tương ứng với một đường). Chúng ta cũng sẽ coi việc giải ra nghiệm của hệ như là đã dựng được giao điểm vậy (thông dịch phép dựng giao điểm)
Tóm lại, dựng hình bằng đại số, hay dựng hình theo ngôn ngữ đại số chính là việc lập phương trình và hệ phương trình, giải phương trình và hệ phương trình.
Đã có trong đầu đoạn từ điển, các tiên đề và định lý hình học, kỹ năng giải phương trình và hệ phương trình bậc một và bậc hai, các phép dựng nền tảng, và các bài toán cần giải. Cái chúng ta thiếu để bắt đầu là những đối tượng hình học cho trước (tạm gọi đây là cơ sở dựng hình). Đến đây, mình có một nhận định rằng chúng ta chỉ cần một loại đối tượng hình học là điểm để làm cơ sở dựng hình mà thôi, bởi vì những đối tượng lớn hơn như đường thẳng và đường tròn đều dựng được từ các điểm phân biệt. Hãy gọi những điểm trong một cơ sở dựng hình là các điểm cơ sở.
Khái niệm cơ sở dựng hình là cần thiết vì một công việc như dựng hình có phần khởi đầu. Cũng như để chứng minh các bài toán hình học, con người bắt đầu từ một hệ tiên đề.
2.4. Số dựng được và các phép toán đại số tương ứng với thao tác dựng hình
Việc thông dịch từ điểm thành bộ hai số thực có thứ tự cho phép chúng ta chuyển từ điểm thành số (cụ thể là hai số). Ứng với điểm dựng được sẽ là số dựng được.
Định nghĩa Điểm dựng được. Cho trước cơ sở dựng hình gồm hai điểm $(0, 0)$ và $(1, 0)$. Một điểm được gọi là dựng được nếu như có thể áp dụng các phép dựng hình nền tảng và xuất phát từ hai điểm $(0, 0)$ và $(1, 0)$ để dựng ra được điểm đó.
Thực ra định nghĩa trên rất straightforward đến mức bạn đọc có thể nghi ngờ sự cần thiết của nó.
Định nghĩa Số dựng được. Cho trước cơ sở dựng hình gồm hai điểm $(0, 0)$ và $(1, 0)$. Một số thực $r$ được gọi là dựng được nếu như từ cơ sở dựng hình trên, chúng ta có thể dựng được điểm $(r, 0)$.
Từ định nghĩa này, chúng ta rút ra được tính chất đầu tiên:
Sự tương đương giữa số dựng được và điểm dựng được. Trong mặt phẳng tọa độ, một điểm là dựng được nếu và chỉ nếu hoành độ và tung độ của điểm đó đều là các số dựng được.
Ví dụ: Các điểm $(n, m)$ (trong đó $n$, $m$ là các số nguyên) là các điểm dựng được. Như vậy các số nguyên đều dựng được. Hơn nữa, các các điểm có tọa độ hữu tỉ cũng dựng được (nhờ có định lý Thales).
Có một câu hỏi cũng như cơ hội ở đây. Đó là từ một cơ sở dựng hình, những số nào là số dựng được? Hay nói cách khác, số dựng được có dấu hiệu nhận biết nào? Trước khi phát biểu dấu hiệu đó, mình đưa ra hai bổ đề và tóm lược ý tưởng chứng minh hai bổ đề đó.
Bổ đề 1. Cho $a$ và $b$ là các số dựng được. Khi đó các số $a + b$, $a - b$, $a\cdot b$, $a/b$ (nếu $b\ne 0$) và $\sqrt{ab}$ (nếu $ab\ge 0$) cũng là các số dựng được.
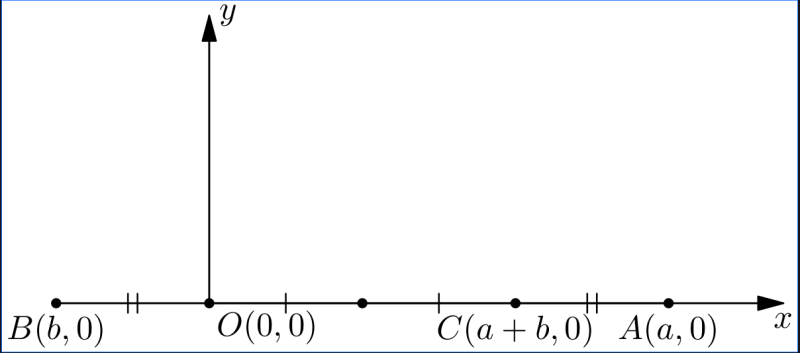
Tóm lược cách chứng minh bổ đề. Kí hiệu $O$ là gốc tọa độ của mặt phẳng tọa độ. $A$ là điểm có tọa độ $(a, 0)$, và $B$ là điểm có tọa độ $(b, 0)$.
Điểm có tọa độ $(a+b, 0)$ là điểm đối xứng với $O$ qua trung điểm của đoạn thẳng $AB$.
Dựng điểm có tọa độ $(a+b, 0)$
Điểm có tọa độ $(b, 0)$ dựng được thì điểm có tọa độ $(-b, 0)$ cũng đựng được (chúng ta dựng điểm đối xứng với $B$ qua $O$). Theo kết quả vừa chứng minh thì $a - b = a + (-b)$ là một số dựng được.
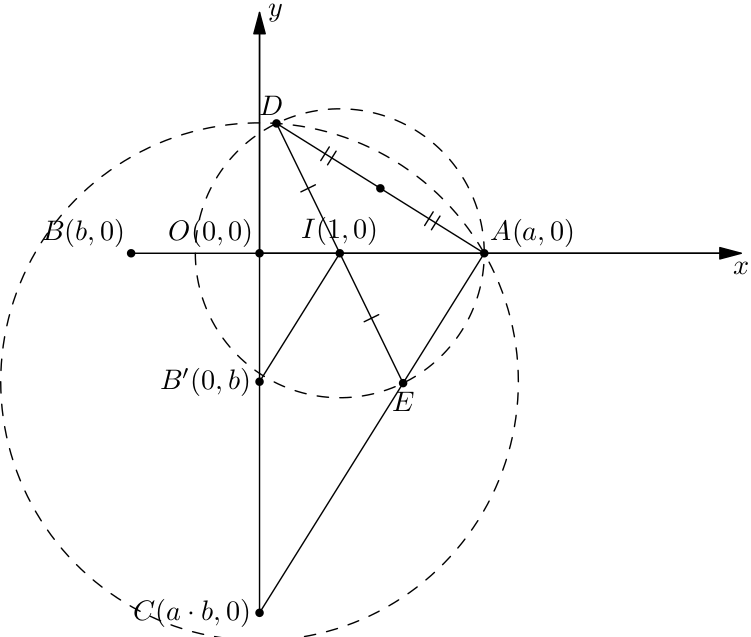
Nếu một trong hai số bằng 0 thì $a\cdot b = 0$, và số $a\cdot b$ dựng được. Nếu một trong hai số bằng 1 thì $a\cdot b$ bằng số còn lại, và dựng được. Với trường hợp còn lại (cả hai số khác 0 và 1), chúng ta lần lượt thực hiện các bước sau
- Dựng điểm $B'$ có tọa độ $(0, b)$.
- Điểm $I$ có tọa độ $(1, 0)$ có sẵn trong cơ sở dựng hình.
- Dựng đường tròn tâm $B'$ và đi qua $A$, dựng đường tròn tâm $I$ và đi qua $A$. Dựng giao điểm $D$ của hai đường tròn này. $D$ cũng là điểm đối xứng với $A$ qua đường thẳng $IB'$.
- Dựng giao điểm $E$ khác $D$ của đường thẳng $ID$ với đường tròn tâm $I$ và đi qua $D$. Điểm $E$ cũng là điểm đối xứng với $D$ qua $I$. Vì $IB'$ không vuông góc với $IA$ nên $IB'$ không vuông góc với $ID$, dẫn tới $DE$ không vuông góc với $IB'$. Mà $DA$ có vuông góc với $IB'$. Do đó $A$ và $E$ là hai điểm phân biệt.
- Đường thẳng $AE$ song song với $IB'$ (theo định lý về đường trung bình của tam giác).
- Dựng $C$ là giao điểm của $AE$ với $OB'$. Theo định lý Thales, $\dfrac{\overline{OC}}{\overline{OB'}} = \dfrac{\overline{OA}}{\overline{OI}}$. Theo đó, tọa độ của $C$ là $(0, a\cdot b)$.
- Dựng giao điểm của đường tròn tâm $O$, đi qua $C$ với đường thẳng $OA$, chúng ta thu được hai điểm $(\pm a\cdot b, 0)$.
Dựng điểm có tọa độ $(a\cdot b, 0)$
Để dựng điểm có tọa độ $(a/b, 0)$, chúng ta dựng điểm có tọa độ $(1/b, 0)$ và áp dụng phép dựng phép nhân vừa rồi. Nếu $b = \pm 1$, chúng ta dựng xong vì đã có sẵn điểm $(1, 0)$ và có thể dựng điểm $(-1, 0)$.
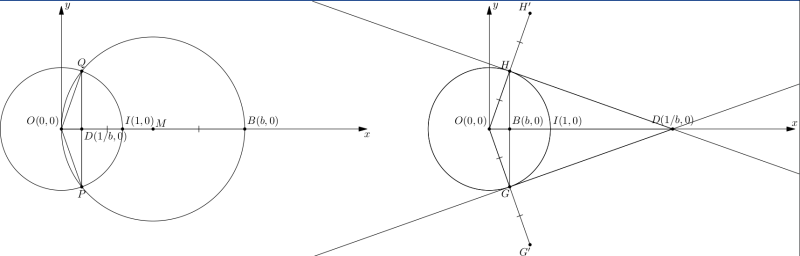
Nếu $\vert b\vert > 1$, chúng ta dựng như sau:
- Dựng đường tròn đơn vị (tâm là $O$ và đi qua $I$)
- Dựng đường trung trực của đoạn thẳng $OB$ (dựng đường tròn tâm $B$ và đi qua $O$, dựng đường tròn tâm $O$ và đi qua $B$, đường thẳng đi qua giao điểm của hai đường tròn này là đường trung trực của đoạn thẳng $OB$).
- Dựng giao điểm của đường thẳng $OB$ với đường trung trực của đoạn thẳng $OB$, chúng ta thu được trung điểm của đoạn thẳng $OB$. Đặt tên điểm này là $M$.
- Dựng đường tròn tâm $M$ và đi qua $O$. Dựng giao điểm của đường tròn này với đường tròn đơn vị. Dựng giao điểm của hai đường tròn này (đặt tên là $P, Q$). Dựng giao điểm của đường thẳng $PQ$ với đường thẳng $OA$, đặt tên điểm này là $D$.
- Vì bình phương độ dài cạnh tam giác vuông bằng tích độ dài cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền, chúng ta áp dụng định lý này cho tam giác $ODP$ và chỉ ra được rằng tọa độ của điểm $D$ là $(1/b, 0)$.
Nếu $\vert b \vert < 1$, chúng ta dựng như sau
- Dựng đường tròn đơn vị.
- Dựng đường tròn tâm $B$ và đi qua $O$. Dựng giao điểm của đường tròn này với đường thẳng $OB$. Một trong hai giao điểm là $O$, giao điểm còn lại, chúng ta đặt tên là $F$.
- Dựng đường trung trực của đoạn thẳng $OF$ (dựng đường tròn tâm $O$ và đi qua $F$, dựng đường tròn tâm $F$ và đi qua $O$, đường thẳng đi qua giao điểm của hai đường tròn này là đường trung trực của đoạn thẳng $OF$). Đường trung trực của đoạn thẳng $OF$ chính là đường thẳng đi qua $B$ và vuông góc với $OB$.
- Dựng giao điểm của đường tròn đơn vị và đường trung trực của đoạn thẳng $OF$. Đặt tên hai giao điểm là $G$ và $H$.
- Dựng điểm $G'$ đối xứng với $O$ qua $G$ và điểm $H'$ đối xứng với $O$ qua $H$.
- Dựng đường trung trực của đoạn thẳng $OG'$ và $OH'$ (với cách dựng đường trung trực như thực hiện trên). Hai đường trung trực này cũng lần lượt là đường thẳng qua $G$ và vuông góc với $OG$, đường thẳng qua $H$ và vuông góc với $OH$.
- Dựng giao điểm của hai đường trung trực vừa dựng, đặt tên giao điểm là $D$. Hai tam giác vuông $ODG$ và $ODH$ bằng nhau theo trường hợp cạnh huyền và cạnh góc vuông. Do đó $DG = DH$. Như vậy $D$ thuộc đường trung trực của đoạn thẳng $GH$, tức là $D$ thuộc đường thẳng $OA$.
- Để chứng minh tọa độ của $D$ là $(1/b, 0)$, chúng ta sử dụng định lý giống với trường hợp trước (áp dụng cho tam giác vuông $ODG$).
Dựng điểm có tọa độ $(1/b, 0)$
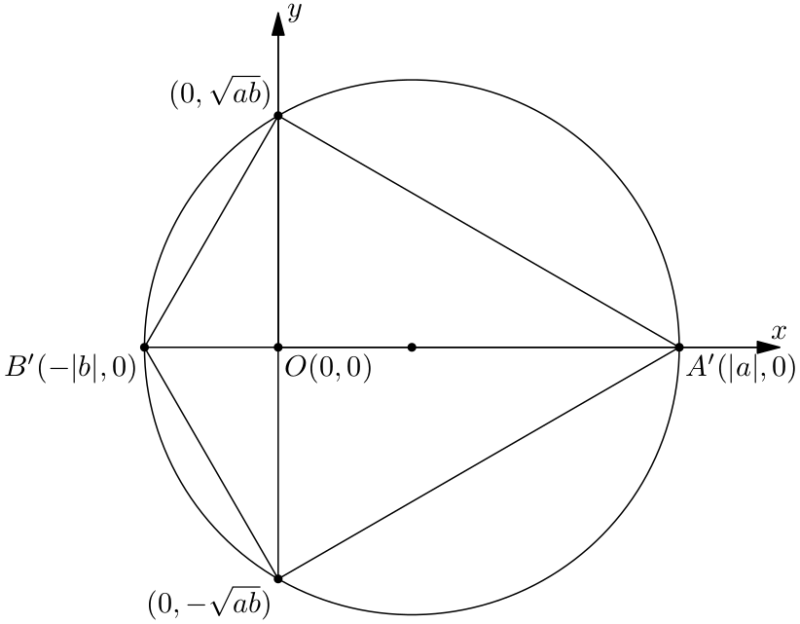
Để dựng điểm có tọa độ $(\sqrt{ab}, 0)$, chúng ta sử dụng định lý: trong tam giác vuông, bình phương độ dài đường cao tương ứng với cạnh huyền bằng tích độ dài hình chiếu của hai cạnh góc vuông lên cạnh huyền. Nếu một trong hai số bằng không, chuyện đã xong vì gốc tọa độ $(0,0)$ thuộc cơ sở dựng hình. Nếu cả hai khác không và $ab > 0$, chúng ta dựng hai điểm $A'$ có tọa độ $(\vert a\vert, 0)$ và $B'$ có tọa độ $(-\vert b\vert, 0)$, rồi dựng hai giao điểm của trục $Oy$ với đường tròn đường kính $A'B'$. Hai giao điểm mới này có tọa độ là $(0, -\sqrt{ab})$ và $(0, \sqrt{ab})$. Có được hai điểm này thì chúng ta dựng được điểm có tọa độ $(\sqrt{ab}, 0)$.
Dựng điểm có tọa độ $(0, \pm\sqrt{ab})$
$\blacksquare$
Bổ đề 2. Trong mặt phẳng tọa độ,
- một đường thẳng là dựng được khi và chỉ khi phương trình đường thẳng đó có thể viết ở dạng $ax + by + c = 0$ và $a, b, c$ là các số dựng được,
- một đường tròn là dựng được khi và chỉ khi phương trình đường tròn đó có thể viết ở dạng ${(x - a)}^{2} + {(y - b)}^{2} = {r}^{2}$ và $a, b, r$ là các số dựng được.
Chứng minh bổ đề.
Phần 1.a. Bắt đầu bằng Phương trình đường thẳng $\ell$ có thể viết ở dạng $ax + by + c = 0$ và $a, b, c$ là các số dựng được.
Nếu $a = 0$ thì đường thẳng $\ell$ đi qua hai điểm có tọa độ là $\left(0, \frac{-c}{b}\right)$ và $\left(1, \frac{-c}{b}\right)$. Theo bổ đề 1 thì tọa độ của hai điểm này là các số dựng được, tức là hai điểm dựng được, và đường thẳng $\ell$ dựng được.
Nếu $a\ne 0$ thì đường thẳng $\ell$ đi qua hai điểm có tọa độ là $\left( 0, \frac{-c}{b} \right)$ và $\left(1, \frac{-c-a}{b}\right)$. Theo bổ đề 1 thì tọa độ của hai điểm này là các số dựng được, tức là hai điểm dựng được, và đường thẳng $\ell$ dựng được.
Phần 1.b. Bắt đầu bằng Đường thẳng $\ell$ dựng được.
Nếu $\ell$ vuông góc với trục hoành thì chúng ta dựng được giao điểm của $\ell$ với đường thẳng có phương trình $y = 0$ và đường thẳng có phương trình $y = 1$. Tọa độ của hai giao điểm lần lượt là $(x_{0}, 0)$ và $(x_{0}, 1)$. Đây là hai điểm dựng được, nên $x_{0}$ là số dựng được. Một phương trình của đường thẳng $\ell$ là $x - x_{0} = 0$.
Nếu $\ell$ không vuông góc với trục hoành thì chúng ta dựng được giao điểm của $\ell$ với đường thẳng có phương trình $x = 0$ và đường thẳng có phương trình $x = 1$. Tọa độ của hai giao điểm lần lượt là $(0, y_{0})$ và $(1, y_{1})$. Đây là hai điểm dựng được, nên $y_{0}, y_{1}$ là các số dựng được. Một phương trình của đường thẳng $\ell$ là $(y_{1} - y_{0})x - y + y_{0} = 0$.
Phần 2.a. Bắt đầu bằng Phương trình đường tròn $(S)$ có thể viết ở dạng ${(x - a)}^{2} + {(y - b)}^{2} = {r}^{2}$ và $a, b, r$ là các số dựng được.
$a$ và $b$ là các số dựng được nên điểm $K$ có tọa độ $(a, b)$ dựng được. $r$ là số dựng được nên điểm $M$ có tọa độ $(r, 0)$ dựng được. Dựng điểm $N$ sao cho $\overrightarrow{KN} = \overrightarrow{OM}$ ($O$ là gốc tọa độ). Đường tròn tâm $K$ và đi qua $N$ có phương trình như trên. Do đó đường tròn $(S)$ dựng được.
Phần 2.b. Bắt đầu bằng Đường tròn $(S)$ dựng được.
Ít nhất một trong hai điểm có tọa độ $(0, 0)$ và $(1, 0)$ không trùng với tâm của đường tròn $(S)$. Dựng đường thẳng đi qua điểm đó và tâm của đường tròn $(S)$. Dựng giao điểm của đường thẳng này và đường tròn $(S)$. Hai giao điểm này dựng được và có tọa độ lần lượt là $(x_{1}, y_{1})$, $(x_{2}, y_{2})$. Hoành độ và tung độ của hai điểm này là các số dựng được. Như vậy, đường tròn $(S)$ có phương trình
\[ {\left( x - \frac{1}{2}(x_{1} + x_{2}) \right)}^{2} + {\left( y - \frac{1}{2}(y_{1} + y_{2}) \right)}^{2} = \frac{1}{4}{(x_{2} - x_{1})}^{2} + \frac{1}{4}{(y_{2} - y_{1})}^{2}. \]
có hệ số là các số dựng được.
$\blacksquare$
Định lý về dấu hiệu nhận biết số dựng được. Một số thực là số dựng được khi và chỉ khi số đó viết được dưới dạng biểu thức chỉ gồm hữu hạn các số nguyên và năm phép toán cộng, trừ, nhân, chia, và căn bậc hai.
Giải thích (Mình gọi là giải thích, không phải chứng minh vì có một nhận định còn để ngỏ).
Chiều thuận. Cho $r$ là một số viết được dưới dạng biểu thức chỉ gồm hữu hạn các số nguyên và năm phép toán cộng, trừ, nhân, chia, và căn bậc hai. Chúng ta sẽ chứng minh bằng quy nạp rằng $(r, 0)$ là điểm dựng được, bằng cách quy nạp theo số lần xuất hiện của các phép toán trong biểu thức của số $r$.
Nếu có $0$ phép toán trong biểu thức của $r$ thì $r$ là số nguyên. Mọi số nguyên đều là số dựng được. Vẫn bằng phép quy nạp toán học, thông qua quan hệ $n = (n - 1) + 1$, cùng với bổ đề trên, chúng ta rút ra được rằng mọi số nguyên dương đều dựng được. Nếu số $a$ dựng được thì số $(-a)$ cũng dựng được. Do đó mọi số nguyên âm đều dựng được.
Giả thiết quy nạp: số thực viết được dưới dạng biểu thức gồm hữu hạn các số nguyên và năm phép toán cộng, trừ, nhân, chia, và căn bậc hai, trong đó các phép toán xuất hiện $n$ lần thì số thực đó là số dựng được.
Chúng ta xét một số thực $r$ viết được dưới dạng biểu thức gồm hữu hạn các số nguyên và năm phép toán cộng, trừ, nhân, chia, và căn bậc hai, trong đó các phép toán xuất hiện $(n+1)$ lần. Do thứ tự thực hiện phép tính, sẽ có phép toán trong biểu thức của $r$ được thực hiện sau cùng. Nếu phép toán sau cùng là một trong các phép toán cộng, trừ, nhân, chia thì theo giả thiết quy nạp, hai toán hạng là các số dựng được và theo bổ đề, $r$ là số dựng được. Còn nếu phép toán sau cùng là căn bậc hai thì theo giả thiết quy nạp $r^{2}$ dựng được (vì biểu thức của $r^{2}$ có $n$ phép toán), và theo bổ đề thì $r$ là số dựng được.
Theo nguyên lý quy nạp, $r$ dựng được.
Chiều đảo. Cho $r$ là một số dựng được.
Các phép dựng nền tảng (được định nghĩa không hình thức ở mục 2.1):
- hoặc tương ứng với việc thiết lập phương trình (dựng đường thẳng đi qua hai điểm và đường tròn với tâm là điểm cho trước, đi qua một điểm cho trước),
- hoặc tương ứng với việc giải phương trình và hệ phương trình bậc một (phương trình đường thẳng) và phương trình bậc hai (phương trình đường tròn). Dựng giao điểm hai đường thẳng tương ứng với giải hệ hai phương trình bậc nhất hai ẩn. Dựng giao điểm đường thẳng và đường tròn tương ứng với giải hệ gồm phương trình đường thẳng và phương trình đường tròn. Dựng giao điểm hai đường tròn tương ứng với giải hệ gồm hai phương trình đường tròn.
Nhận định sau cần được chứng minh chặt chẽ và cover nhiều trường hợp, tuy nhiên mình chưa thể chứng minh và để NGỎ, đó là: Mọi phép dựng được hợp thành bởi các phép dựng nền tảng nêu trên.
Theo định nghĩa của số dựng được, điểm có tọa độ $(r, 0)$ dựng được. Nói rõ hơn, điểm này dựng được sau khi áp dụng hữu hạn lần các phép dựng nền tảng. Chúng ta sẽ chứng minh rằng khi bắt đầu từ một cơ sở dựng hình gồm các điểm dựng được thì
- Phương trình đường thẳng đi qua hai điểm dựng được nhận hệ số là các số dựng được.
- Phương trình đường tròn với tâm là điểm dựng được, đi qua một điểm dựng được cũng nhận hệ số là các số dựng được.
- Giao điểm hai đường thẳng (mỗi đường thẳng đi qua hai điểm dựng được) là một điểm dựng được.
- Giao điểm một đường thẳng (đi qua hai điểm dựng được) với một đường tròn (có tâm là điểm dựng được, đi qua một điểm dựng được) là các điểm dựng được.
- Giao điểm hai đường tròn (mỗi đường tròn có tâm là điểm dựng được, đi qua điểm dựng được) là các điểm dựng được.
Phần 1. Ký hiệu tọa độ hai điểm dựng được là $(x_{1}, y_{1})$ và $(x_{2}, y_{2})$. Hoành độ và tung độ của mỗi điểm là các số dựng được.
Phương trình đường thẳng đi qua hai điểm này là
\[ (y_{2} - y_{1})(x - x_{1}) - (x_{2} - x_{1})(y - y_{1}) = 0.\]
Theo bổ đề trên, hệ số trong phương trình đường thẳng này là các số dựng được.
Từ phần 1 này, ta suy ra rằng một đường thẳng là dựng được khi và chỉ khi phương trình đường thẳng đó có thể viết ở dạng mà các hệ số đều là các số dựng được.
Phần 2. Ký hiệu tọa độ hai điểm dựng được là $(x_{1}, y_{1})$ và $(x_{2}, y_{2})$.
Phương trình đường tròn với tâm có tọa độ $(x_{1}, y_{1})$, đi qua điểm có tọa độ $(x_{2}, y_{2})$ là
\[ {(x-x_{1})}^{2} + {(y - y_{1})}^{2} = {(x_{2}-x_{1})}^{2} + {(y_{2} - y_{1})}^{2} \]
Theo bổ đề trên, hệ số trong phương trình đường tròn này là các số dựng được.
Phần 3. Cả hai đường thẳng đi qua hai điểm dựng được nên phương trình của chúng có thể viết ở dạng $a_{1}x + b_{1}y + c_{1} = 0$ và $a_{2}x + b_{2}y + c_{2} = 0$ với hệ số là những số dựng được. Tọa độ giao điểm của hai đường thẳng thu được thông qua việc giải hệ hai phương trình trên. Tọa độ đó là
\[ \left(-\frac{c_{1}b_{2} - c_{2}b_{1}}{a_{1}b_{2} - a_{2}b_{1}}, -\frac{a_{1}c_{2} - a_{2}c_{1}}{a_{1}b_{2} - a_{2}b_{1}}\right) \]
Hai thành phần tọa độ đều là các số dựng được, theo bổ đề 1. ($a_{1}b_{2} - a_{2}b_{1}\ne 0$ vì hai đường thẳng cắt nhau)
Phần 4. Đường thẳng có phương trình $ax + by + c = 0$, đường tròn có phương trình ${(x - x_{0})}^{2} + {(y - y_{0})}^{2} = {r}^{2}$, trong đó $a, b, c, x_{0}, y_{0}, r$ là các số dựng được. Giao điểm của đường thẳng và đường tròn là nghiệm của hệ hai phương trình trên. Chúng ta đưa ra cách giải
Nếu $a = 0$ thì $y = \frac{-c}{b}$ và là một số dựng được. Chúng ta thế giá trị này vào phương trình đường tròn, thu được một phương trình bậc hai với ẩn $x$, hệ số là các số dựng được. Do công thức nghiệm của phương trình bậc hai chỉ gồm các phép toán cộng, trừ, nhân, chia, căn bậc hai và thực hiện trên các hệ số của phương trình, nên nghiệm cũng là các số dựng được.
Nếu $a\ne 0$ thì $x = \frac{-by - c}{a}$. Chúng ta thế $x = \frac{-by - c}{a}$ vào phương trình đường tròn, thu được một phương trình bậc hai với ẩn $y$, hệ số là các số dựng được. Bằng lập luận giống hệt trường hợp trước, chúng ta kết luận nghiệm của phương trình bậc hai đó cũng là các số dựng được.
Tóm lại giao điểm của đường thẳng và đường tròn như giả thiết là các điểm dựng được.
Phần 5. Hai đường tròn có phương trình lần lượt là ${(x - x_{1})}^{2} + {(y - y_{1})}^{2} = {r_{1}}^{2}$ và ${(x - x_{2})}^{2} + {(y - y_{2})}^{2} = {r_{2}}^{2}$. Tọa độ giao điểm hai đường tròn cũng là nghiệm của hệ hai phương trình trên.
Bằng cách trừ phương trình thứ nhất cho phương trình thứ hai, chúng ta thu được một phương trình bậc nhất hai ẩn. Vậy là chúng ta đã quy Phần 5 về Phần 4. Như vậy giao điểm hai đường tròn như giả thiết là các điểm dựng được.
Trong cả 5 phép dựng nền tảng, hệ số của phương trình đường thẳng, đường tròn là các số dựng được; giao điểm của các đường dựng được có tọa độ là những số dựng được. Những tọa độ đó, hệ số đó đều được cấu thành từ số nguyên (vì cơ sở dựng hình là hai điểm $(0, 0)$ và $(1, 0)$), và hữu hạn lần xuất hiện các phép toán cộng, trừ, nhân, chia, và căn bậc hai. Cùng với việc điểm $(r, 0)$ dựng được, chúng ta kết luận là $r$ có thể được viết dưới dạng biểu thức gồm hữu hạn số nguyên, các phép toán cộng, trừ, nhân, chia, và căn bậc hai. $\blacksquare$
Căn bậc hai là phép toán lạc loài nhất ở đây, và cũng góp phần tạo nên sự phức tạp trong hệ sinh thái của các số dựng được, bởi vì trong biểu thức của một số dựng được, căn bậc hai có thể được áp dụng nhiều lần, và lồng nhau. Để kết thúc phần này và đi tiếp đến chứng minh, mình đưa ra thêm ví dụ về số dựng được:
$$\sqrt{2}, \sqrt{3}, \frac{1 + \sqrt{5}}{2}, \sqrt[4]{2}, \sqrt{\frac{1 + \sqrt{2}}{\sqrt{3} - \sqrt[4]{2}}}, \sqrt{3 + \sqrt{5 - \sqrt{6}} + \sqrt[8]{7}}$$
Lưu ý rằng đối với một số dựng được, biểu thức cho số đó mà chỉ gồm hữu hạn số nguyên, phép cộng, trừ, nhân, chia và căn bậc hai không phải là duy nhất. Ngoài ra, có những số có thể viết dưới dạng biểu thức mà có phép toán căn bậc ba, nhưng vẫn viết theo dạng trên được, chẳng hạn $\sqrt[3]{8} = 2$.
3. Một chút đại số trừu tượng
Như đã cảnh báo ở mục 1, chứng minh dùng đến kiến thức toán học nằm ngoài chương trình phổ thông. Mục 3 này nói về phần kiến thức đó ở mức đủ dùng cho chứng minh. Dưới đây là một chút đại số trừu tượng.
Tại sao lại gọi là đại số trừu tượng, nó khác gì đại số? Hmm, là một kẻ ngoại đạo với Toán, mình sẽ nói thế này: Ý tưởng cơ bản nhất của đại số là thực hiện các phép toán trên các số và kí hiệu. Chỉ cần tới các kí hiệu, phép toán và luật (tính chất của phép toán) là làm việc được. Cái mà học sinh phổ thông làm việc cùng là đại số sơ cấp. Còn đại số trừu tượng thì tiến thêm, khi mà nhánh này giới thiệu những cấu trúc đại số. Thực ra học sinh phổ thông đã được làm việc với một cấu trúc đại số rất nhiều, đó là trường (Field), cụ thể là trường số hữu tỉ, trường số thực, trường số phức. Chỉ là chưa từng được định nghĩa hay gọi chúng với những cái tên như vậy.
3.1. Định nghĩa trường
Khi đọc phần dưới, bạn đọc có thể cảm thấy người viết hơi lẩm cẩm khi mà viết ra những thứ quá đỗi quen thuộc. Mình có một yêu cầu nhỏ: bạn đọc hãy đọc danh sách 9 tính chất bên dưới với những ý niệm sau
- Không (chưa) cần biết phép cộng và nhân là gì.
- Mỗi gạch đầu dòng ở ngay bên dưới là những tiên đề (hãy thừa nhận chúng).
- Không đồng nhất kí hiệu với những gì đã biết ở số thực.
(Một trong những bài học chí mạng mà mình mất vài năm để rút ra đấy là: Khi học Toán, có những lúc cần biết chấp nhận những gì bản thân chưa hiểu để đi tiếp)
Cho trước một tập hợp $\mathbb{F}$ khác rỗng và hai luật hợp thành, hay phép toán, lần lượt gọi là phép cộng (kí hiệu $+$) và phép nhân (kí hiệu $\cdot$). Ở hai phép toán này, ta kết hợp phần tử của $\mathbb{F}$ và tương ứng chúng với một phần tử nữa. Theo ngôn ngữ tập hợp và ánh xạ:
$$\begin{align*}+:\quad& \mathbb{F}\times\mathbb{F} \to \mathbb{F} \\ & (a, b) \mapsto a + b \end{align*}$$
$$\begin{align*}\cdot:\quad& \mathbb{F}\times\mathbb{F} \to \mathbb{F} \\ & (a, b) \mapsto a\cdot b\end{align*}$$
Người ta còn phát biểu rằng: $\mathbb{F}$ đóng với phép cộng và nhân.
Tập hợp $\mathbb{F}$ cùng với hai phép toán đó được gọi là một trường nếu chúng thỏa mãn 9 tính chất sau (được gọi là 9 tiên đề về Trường)
- (F1) Phép cộng có tính chất kết hợp (Addition is associative): Với mọi phần tử $a, b, c$ của $\mathbb{F}$
- $$(a + b) + c = a + (b + c)$$
- (F2) Phép cộng có phần tử đồng nhất, hay trung lập (Addition has an identity element): Tồn tại một phần tử của $\mathbb{F}$, kí hiệu là $0$ sao cho với mọi $a$ thuộc $\mathbb{F}$ thì
- $$a + 0 = 0 + a = a$$
- (F3) Mỗi phần tử của $\mathbb{F}$ đều có phần tử đối (Each element has an additive inverse): Với mỗi $a$ thuộc $\mathbb{F}$, tồn tại một phần tử được kí hiệu là $(-a)$ sao cho
- $$a + (-a) = (-a) + a = 0$$
- (F4) Phép cộng có tính chất giao hoán (Addition is commutative): Với mọi phần tử $a$, $b$ thì
- $$a + b = b + a$$
- (F5) Phép nhân có tính chất kết hợp (Multiplication is associative): Với mọi phần tử $a, b, c$ của $\mathbb{F}$
- $$(a \cdot b) \cdot c = a \cdot (b \cdot c)$$
- (F6) Phép nhân có tính chất phân phối với phép cộng (Multiplication is distributive over addition): Với mọi phần tử $a, b, c$ của $\mathbb{F}$
- $$a\cdot (b + c) = a\cdot b + a\cdot c\qquad (b + c)\cdot a = b\cdot a + c\cdot a$$
- (F7) Phép nhân có phần tử đồng nhất, hay đơn vị (Multiplication has an identity element): Tồn tại một phần tử của $\mathbb{F}$, kí hiệu là $1$ (khác $0$) sao cho với mọi $a$ thuộc $\mathbb{F}$ thì
- $$a\cdot 1 = 1\cdot a = a$$
- (F8) Phép nhân có tính chất giao hoán (Multiplication is commutative): Với mọi phần tử $a$, $b$ của $\mathbb{F}$ thì
- $$a\cdot b = b\cdot a$$
- (F9) Mỗi phần tử khác $0$ đều có nghịch đảo (Every non-zero element has a multiplicative inverse): Với mỗi phần tử $a\ne 0$ thuộc $\mathbb{F}$, tồn tại phần tử (kí hiệu là) ${a}^{-1}$ thuộc $\mathbb{F}$ sao cho
- $$a\cdot {a}^{-1} = {a}^{-1}\cdot a = 1$$
Sau đây là vài ví dụ và phản ví dụ về trường:
- Tập hợp số thực với hai phép toán cộng và nhân đã được học là một trường.
- Tập hợp số hữu tỉ với hai phép toán cộng và nhân đã được học là một trường.
- Tập hợp số phức với hai phép toán cộng và nhân đã được học là một trường.
- Tập hợp số tự nhiên với hai phép toán cộng và nhân đã được học là không phải một trường.
- Tập hợp số nguyên với hai phép toán cộng và nhân đã được học là không phải một trường.
- (Đây là ví dụ không hiển nhiên nhất trong danh sách này) Tập hợp $J = \{ a + b\sqrt{2} \vert a, b\in\mathbb{Q} \}$ với hai phép toán cộng và nhân đã học là một trường.
Hãy nói thêm về ví dụ cuối cùng. Để kiểm tra $J$ (cùng hai phép toán) có phải một trường không, ta không cần kiểm tra từng tính chất. Bởi vì các phần tử của $J$ cũng là các số thực, nên chỉ cần kiểm tra:
- Số $0$ và số $1$ thuộc $J$.
- Phép cộng thông thường hai phần từ của $J$ cho ra một phần tử của $J$.
- Phép nhân thông thường hai phần từ của $J$ cho ra một phần tử của $J$.
- Phần tử đối của $J$ cũng thuộc $J$.
- Phần tử nghịch đảo của $J$ cũng thuộc $J$.
4. Chứng minh của Edmund Landau
Edmund Landau là một nhà toán học làm việc trong lĩnh vực lý thuyết số người Đức. Trong cuốn Mathematics and Its History, tác giả John Stillwell viết rằng Edmund Landau đã đưa ra lời giải cho bài toán gấp đôi thể tích khối lập phương khi còn là sinh viên, và chứng minh của Landau là sơ cấp. Nếu chẳng may bạn đọc bỏ quên mục 1, mình viết lại ở đây rằng: Trong bài viết này, mình cố gắng tái hiện chứng minh của Landau theo ý tưởng trong cuốn sách, bởi mình chưa tìm ra chứng minh nguyên bản.
4.1. Các trường số dựng được
Đầu tiên, chúng ta xây dựng các trường số dựng được (là trường gồm toàn là các số dựng được). Cái khó khăn ở đây là căn bậc hai có thể lồng nhau nhiều lần tùy ý, miễn sao hữu hạn. Landau xây dựng chúng bằng quan hệ hồi quy.
- $F_{0} = \mathbb{Q}$ (đây là một trường số dựng được, đó là trường số hữu tỉ)
- Với số nguyên không âm $k$, định nghĩa $F_{k+1} = \{ a + b\sqrt{c_{k}} : a, b \in F_{k} \}$ với một số $c_{k}$ cụ thể thuộc $F_{k}$.
Từ định nghĩa này, chúng ta có thể chỉ ra ngay rằng hai số hữu tỉ $0$ và $1$ thuộc $F_{k}$, với mọi $k$ nguyên không âm, bất kể các số $c_{0}, c_{1}, c_{2},\ldots c_{k-1}$ được chọn như thế nào từ $F_{0}, F_{1}, F_{2},\ldots F_{k-1}$.
Chúng ta chứng minh hai kết quả sau. Cả hai mệnh đề sẽ được chứng minh bằng phương pháp quy nạp toán học.
Mệnh đề 1. $F_{k}$ cùng với phép cộng và nhân hai số thực là một trường với mỗi số nguyên không âm $k$.
Chứng minh mệnh đề 1. Mệnh đề trên đúng với $k = 0$.
Giả sử mệnh đề đúng với $k = n\ge 0$. Chúng ta chứng minh mệnh đề đúng với $k = n + 1$.
Nếu $r$ thuộc $F_{n}$ thì $r = r + 0\sqrt{c_{n}} \in F_{n+1}$. Như vậy $F_{n}\subseteq F_{n+1}$.
Theo định nghĩa của $F_{n+1}$, với mọi $a, b, x, y\in F_{n}$ và $c_{n}\ge 0 \in F_{n}$, $a + b\sqrt{c_{n}}$ và $x + y\sqrt{c_{n}}$ là hai phần tử của $F_{n+1}$.
Bước 1. $F_{n+1}$ đóng với phép cộng.
$(a + b\sqrt{c_{n}}) + (x + y\sqrt{c_{n}}) = (a + x) + (b + y)\sqrt{c_{n}}$. Theo giả thiết quy nạp, $a + x\in F_{n}$ và $b + y\in F_{n}$. Do đó $(a + b\sqrt{c_{n}}) + (x + y\sqrt{c_{n}}) \in F_{n+1}$.
Bước 2. $F_{n+1}$ đóng với phép nhân.
$(a + b\sqrt{c_{n}}) \cdot (x + y\sqrt{c_{n}}) = (ax + byc_{n}) + (bx + ay)\sqrt{c_{n}}$. Theo giả thiết quy nạp, $ax + byc_{n}\in F_{n}$ và $bx + ay\in F_{n}$. Do đó $(a + b\sqrt{c_{n}}) \cdot (x + y\sqrt{c_{n}}) \in F_{n+1}$.
Bước 3. Số đối của $a + b\sqrt{c_{n}}$ là $(-a) + (-b)\sqrt{c_{n}}$, cũng thuộc $F_{n+1}$, vì $(-a), (-b), c_{n}\in F_{n}$.
Bước 4. Nếu $a + b\sqrt{c_{n}} \ne 0$ thì nghịch đảo của $a + b\sqrt{c_{n}} \ne 0$ cũng thuộc $F_{n+1}$.
Trường hợp 1. $a = 0, b\ne 0, c_{n}\ne 0$. Lúc này nghịch đảo của $a + b\sqrt{c_{n}}$ là ${\sqrt{c_{n}}}^{-1}{b}^{-1} = \frac{1}{bc_{n}}\sqrt{c_{n}}$. Theo định nghĩa và giả thiết quy nạp, số này thuộc $F_{n+1}$.
Trường hợp 2. $a\ne 0, b = 0$ hoặc $a\ne 0, c_{n} = 0$. Lúc này phần tử nghịch đảo là ${a}^{-1}$. Số này thuộc $F_{n}$ theo giả thiết quy nạp, nên cũng thuộc $F_{n+1}$.
Trường hợp 3. $a, b, c_{n}\ne 0$.
Nếu $a^{2} - b^{2}c_{n}\ne 0$ thì ta có phần tử nghịch đảo $\dfrac{a}{a^{2} - b^{2}c_{n}} + \frac{b\sqrt{c_{n}}}{a^{2} - b^{2}c_{n}}$ thuộc $F_{n+1}$. Nếu $a^{2} - b^{2}c_{n} = 0$ thì $a + b\sqrt{c_{n}} = a + b\cdot\left\vert\frac{a}{b}\right\vert$. Nếu $a$ và $b$ trái dấu thì $a + b\sqrt{c_{n}} = 0$ (mâu thuẫn với giả thiết ban đầu). Còn nếu $a$ và $b$ cùng dấu thì $a + b\sqrt{c_{n}} = 2a$, có nghịch đảo là $\frac{1}{2a}$ thuộc $F_{n}$. Do đó $\frac{1}{2a}$ cũng thuộc $F_{n+1}$.
Như vậy $F_{n+1}$ với hai phép toán cộng và nhân số thực cũng là một trường.
Theo nguyên lý quy nạp, mệnh đề đúng. $\blacksquare$
Mệnh đề 2. Trong mỗi $F_{k}$, tồn tại phần tử $c_{k}$ sao cho $c_{k} > 0$ và $\sqrt{c_{k}}\notin F_{k}$ (lưu ý là chúng ta không nhất thiết dùng số $c_{k}$ này để tạo ra trường $F_{k+1}$). Khi đó với $a, b\in F_{k}$, $a + b\sqrt{c_{k}} = 0$ khi và chỉ khi $a = b = 0$.
Chứng minh mệnh đề 2. Với $k = 0$, $c_{0} = 2$ là một phần tử như vậy.
Chúng ta cần chứng minh Với hai số hữu tỉ $a$ và $b$ mà ta có $a + b\sqrt{2} = 0$ thì $a = b = 0$. Hãy xem xét bốn trường hợp
- $a = 0$ và $b\ne 0$ thì $a + b\sqrt{2}\ne 0$ (mâu thuẫn)
- $a\ne 0$ và $b = 0$ thì $a + b\sqrt{2}\ne 0$ (mâu thuẫn)
- $a, b$ cùng khác không thì $\sqrt{2} = -\dfrac{a}{b}$, tức là $\sqrt{2}\in F_{0}$ (mâu thuẫn)
- $a = b = 0$ thì $a + b\sqrt{2} = 0$.
Do đó $a + b\sqrt{2} = 0$ thì $a = b = 0$.
Giả sử mệnh đề đúng với $k = n\ge 0$.
Số thuộc $F_{n+1}$ có dạng $a + b\sqrt{c_{n}}$, với $a, b\in F_{n}$ và $c_{n}$ là một số cố định thuộc $F_{n}$.
Nếu $\sqrt{c_{n}}\in F_{n}$ thì $a + b\sqrt{c_{n}} \in F_{n}$ (do $F_{n}$ là một trường), kéo theo $F_{n+1} = F_{n}$. Theo giả thiết quy nạp, $F_{n}$ chứa phần tử mà căn bậc hai của nó không thuộc $F_{n}$. Mà $F_{n+1} = F_{n}$ nên $F_{n+1}$ chứa phần tử mà căn bậc hai của nó không thuộc $F_{n+1}$. Ngược lại, nếu $\sqrt{c_{n}}\notin F_{n}$, chúng ta chỉ ra $c_{n+1} = \sqrt{c_{n}}$ thỏa mãn $c_{n+1}\in F_{n+1}$ và $\sqrt{c_{n+1}}\notin F_{n+1}$. Theo định nghĩa của $F_{n}$, $c_{n+1} \in F_{n+1}$.
Giả sử phản chứng rằng $\sqrt{c_{n+1}}\in F_{n+1}$. Khi đó, tồn tại $x, y\in F_{n}$ sao cho $\sqrt{\sqrt{c_{n}}} = x + y\sqrt{c_{n}}$. Bình phương hai vế rồi biến đổi tương đương đẳng thức, chúng ta thu được
\[ x^{2} + y^{2}c_{n} + (2xy - 1)\sqrt{c_{n}} = 0 \]
Lưu ý $c_{n} > 0$. Theo giả thiết quy nạp, $x^{2} + y^{2}c_{n} = 2xy - 1 = 0$. Từ hai đẳng thức này, chúng ta suy ra $2xy = 1$, $x = 0$ và $y = 0$. Điều này dẫn tới $\sqrt{\sqrt{c_{n}}} = 0$. Như vậy giả sử phản chứng $\sqrt{c_{n+1}}\in F_{n+1}$ là sai, tức là $\sqrt{c_{n+1}}\notin F_{n+1}$.
Cuối cùng, nếu $a + b\sqrt{c_{n+1}} = 0$ với $a, b\in F_{n+1}$, chúng ta xem xét bốn trường hợp:
- $a = 0$ và $b\ne 0$ thì $a + b\sqrt{c_{n+1}} = b\sqrt{c_{n+1}}\ne 0$ (mâu thuẫn)
- $a\ne 0$ và $b = 0$ thì $a + b\sqrt{c_{n+1}} = a \ne 0$ (mâu thuẫn)
- $a\ne 0$ và $b\ne 0$ thì $\sqrt{c_{n+1}} = -\dfrac{a}{b} \in F_{n+1}$ (mâu thuẫn)
- $a = b = 0$ thì $a + b\sqrt{c_{n}} = 0$.
Ba trường hợp đầu tiên dẫn đến mâu thuẫn. Do vậy $a + b\sqrt{c_{n+1}} = 0$ thì $a = b = 0$.
Theo nguyên lý quy nạp, mệnh đề đúng. $\blacksquare$
Có một chi tiết mà tác giả Stillwell không đưa ra trong cuốn sách. Đó là câu hỏi: Liệu có cách nào thiết lập các trường $F_{1}, F_{2}, \ldots$ sao cho một số dựng được cho trước sẽ thuộc một trong các trường đó không? Mệnh đề và chứng minh dưới đây khẳng định điều đó.
Mệnh đề 3. Với một tập hợp hữu hạn $C = \{ x_{1}, x_{2}, \cdots, x_{n} \}$ chỉ gồm $n$ số dựng được, ta luôn chọn được các số $c_{0}, c_{1}, \ldots$ và các trường $F_{1}, F_{2}, \ldots$ sao cho các số trong $C$ cùng thuộc một trường $F_{k}$ nào đó.
(Đây là khó khăn riêng của mình với Mệnh đề 3: Ban đầu, mình phát biểu Mệnh đề 3 chỉ gồm đúng một số dựng được thay vì cả một tập hợp to tùy ý và hữu hạn, nhưng rồi mình nhận ra hạn chế của phát biểu đó. Mình thay bằng hai số, thấy vẫn chưa được, rồi ba số, và khi đi đến phát biểu trên thì mình hài lòng.)
Chứng minh mệnh đề 3. Chúng ta chứng minh bằng quy nạp mạnh, cụ thể là quy nạp theo số lần xuất hiện các phép toán trong biểu thức của $C$ (Số dựng được nào có số lần xuất hiện phép toán nhiều nhất? Quy nạp theo số lượng đó).
Khi n = 0 (không dùng phép toán nào). Lúc này các số dựng được đều nguyên và chúng cùng thuộc $F_{0}$.
Khi n = 1 (dùng một phép toán đúng một lần).
Nếu các số dựng được trong $C$ viết được dưới dạng biểu thức gồm đúng một trong bốn phép toán cộng/trừ/nhân/chia và hai số nguyên thì chúng đều là số nguyên, và đều thuộc về trường $F_{0}$.
Nếu trong $C$ có những số cần được viết dạng căn bậc hai của số nguyên thì khác. Trong tập hợp $C$, không mất tính tổng quát, hãy coi như $x_{1}, x_{2}, \ldots x_{m}$ ($m\le n$) là các số được viết dưới dạng căn bậc hai của một số nguyên. Khi đó chúng ta xây dựng các trường $F_{1}, F_{2}, \ldots, F_{m}$ như sau:
- $F_{1} = \{ a + bx_{1} : a, b\in F_{0} \}$
- $F_{2} = \{ a + bx_{2} : a, b\in F_{1} \}$
- $\ddots$
- $F_{m} = \{ a + bx_{m} : a, b\in F_{m-1} \}$.
Như vậy $F_{m}$ là một trường thỏa mãn.
Giả thiết quy nạp: Các số trong $C$ viết được dưới dạng biểu thức với các số nguyên và có không quá $p$ lần xuất hiện các phép toán, và chúng thuộc một trường $F_{k}$ nào đó (đi kèm với sự lựa chọn $c_{0}, c_{1}, \ldots c_{k-1}$ nào đó).
Xét một số dựng được $c$ viết được dưới dạng biểu thức mà các phép toán xuất hiện $(p+1)$ lần. Các phép toán có thứ tự ưu tiên, và khi liệt kê theo độ ưu tiên giảm dần thì chúng ta có danh sách: căn bậc hai, nhân chia, cộng trừ. Nói riêng, các biểu thức ở ngoặc trong cùng được thực hiện trước. Vì biểu thức của $c$ chỉ có hữu hạn các phép toán và giữa chúng có thứ tự ưu tiên, nên sẽ có một phép toán được thực hiện sau cùng.
Nếu phép toán cuối cùng của các số trong $C$ là phép cộng hoặc trừ hoặc nhân hoặc chia, thì theo giả thiết quy nạp, các số đó thuộc trường $F_{k}$.
Nếu có những số $x_{1}, x_{2}, \ldots x_{m}$ ($m\le n$) mà phép toán cuối cùng là căn bậc hai, và các số còn lại $x_{m+1}, x_{m+2}, \ldots, x_{n}$ có phép toán cuối cùng là cộng, trừ, nhân, hoặc chia thì
- $x_{i}$ (với $m < i \ne n$) là tổng, hiệu, tích, hoặc thương của hai số dựng được $a_{i}$ và $b_{i}$ nào đó (cặp số này gồm không quá $p$ lần thực hiện phép toán cộng trừ nhân chia và căn bậc hai).
- $x_{j}$ (với $1\le j \le m$) là căn bậc hai của số dựng được $y_{j}$ nào đó (số $y_{j}$ này gồm không quá $p$ lần thực hiện phép toán cộng trừ nhân chia và căn bậc hai).
Theo giả thiết quy nạp, các số $a_{i}, b_{i} (m < i \le n)$ và $y_{j} (1\le j \le m)$ cùng thuộc một trường $F_{k}$ nào đó (đi kèm là các số $c_{0}\in F_{0}, c_{1}\in F_{1}, \ldots, c_{k-1}\in F_{k-1}$ để thiết lập các trường liên tiếp).
Chúng ta định nghĩa ra các trường khác, nhưng bắt đầu bằng $F_{k}$ thay vì $F_{0}$.
- $F_{k+1} = \{ a + b\sqrt{y_{1}} : a, b \in F_{k} \}$
- $F_{k+2} = \{ a + b\sqrt{y_{2}} : a, b \in F_{k+1} \}$
- $\ddots$
- $F_{k+m} = \{ a + b\sqrt{y_{m}} : a, b \in F_{k+m-1} \}$.
Vậy thì trường $F_{k+m}$ là một trường thỏa mãn.
Theo nguyên lý quy nạp, mệnh đề đúng. $\blacksquare$
4.2. Gấp đôi thể tích khối lập phương
Chúng ta đi đến kết quả chính của bài viết này.
Định lý. $\sqrt[3]{2}$ không phải một số dựng được.
Chứng minh định lý. Trước tiên, chúng ta chứng minh $\sqrt[3]{2}$ là một số vô tỉ.
Giả sử phản chứng rằng $\sqrt[3]{2}$ là một số hữu tỉ.
Khi đó, tồn tại hai số tự nhiên $a$ và $b$ nguyên tố cùng nhau sao cho $\sqrt[3]{2} = \dfrac{a}{b}$. Điều này kéo theo ${a}^{3} = 2{b}^{3}$. Đẳng thức thu được cho thấy ${a}^{3}$ là số chẵn, hay $a$ là số chẵn. Chia hai vế của đẳng thức cho 8, ta được ${\left(\dfrac{a}{2}\right)}^{3} = \dfrac{b^{3}}{4}$. Vì ${\left(\dfrac{a}{2}\right)}^{3}$ là một số tự nhiên nên $\dfrac{b^{3}}{4}$ cũng vậy, tức là $b$ là số chẵn. Chúng ta đã chỉ ra rằng ước chung lớn nhất của $a$ và $b$ không nhỏ hơn $2$, và điều này mẫu thuẫn với việc $a$ và $b$ nguyên tố cùng nhau. Do đó $\sqrt[3]{2}$ là số vô tỉ.
Giả sử phản chứng rằng $\sqrt[3]{2}$ là một số dựng được.
Do $\sqrt[3]{2}$ vô tỉ nên sẽ tồn tại số nguyên không âm $n$ sao cho tồn tại dãy $c_{0}, c_{1}, \ldots, c_{n}$ và $F_{1}, F_{2}, \ldots, F_{n+1}$ sao cho $\sqrt[3]{2}\in F_{n+1}$. Theo Well-Ordering Principle (tập hợp khác rỗng các số nguyên và bị chặn dưới thì có phần tử nhỏ nhất), tồn tại số tự nhiên $k$ nhỏ nhất thỏa mãn: tồn tại dãy $c_{0}, c_{1}, \ldots, c_{k}$ và $F_{1}, F_{2}, \ldots, F_{k+1}$ sao cho $\sqrt[3]{2}\in F_{k+1}$. Nói cách khác, $\sqrt[3]{2}\in F_{k+1}$ và $\sqrt[3]{2}\notin F_{k}$ $(\star)$. Theo định nghĩa của $F_{k+1}$, tồn tại $a, b\in F_{k}$ sao cho $\sqrt[3]{2} = a + b\sqrt{c_{k}}$. Lập phương hai vế, chúng ta thu được
\[ 2 = {a}^{3} + {b}^{3}c_{k}\sqrt{c_{k}} + 3{a}^{2}b\sqrt{c_{k}} + 3{a}{b}^{2}c_{k} \]
đẳng thức trên tương đương với
\[ 0 = ({a}^{3} + 3{a}{b}^{2}c_{k} - 2) + ({b}^{3}c_{k} + 3{a}^{2}b)\sqrt{c_{k}}. \]
Nếu $\sqrt{c_{k}} \in F_{k}$ thì $\sqrt[3]{2} \in F_{k}$, điều này mâu thuẫn với $(\star)$. Do đó $\sqrt{c_{k}}\notin F_{k}$. Theo Mệnh đề 2
\[ {a}^{3} + 3{a}{b}^{2}c_{k} = 2\qquad {b}^{3}c_{k} + 3{a}^{2}b = 0 \]
Từ điều trên, chúng ta có $2 = {a}^{3} + 3{a}{b}^{2}c_{k} - ({b}^{3}c_{k} + 3{a}^{2}b)\sqrt{c_{k}} = {(a - b\sqrt{c_{k}})}^{3}$, dẫn đến $\sqrt[3]{2} = a - b\sqrt{c_{k}}$. $\sqrt[3]{2} = \dfrac{(a + b\sqrt{c_{k}}) + (a - b\sqrt{c_{k}})}{2} = a\in F_{k}$, mâu thuẫn với $(\star)$.
Giả sử phản chứng là sai. Như vậy $\sqrt[3]{2}$ không phải một số dựng được. $\blacksquare$
Việc dựng một khối lập phương có thể tích gấp đôi thể tích một khối lập phương cho trước tương đương với việc dựng số $\sqrt[3]{2}$. Định lý trên và chứng minh đã phủ định sự tồn tại của một phép dựng như vậy.
4.3. Bình luận
Thực ra, việc tạo ra các trường $F_{1}, F_{2}, \ldots$ chính là việc mở rộng trường (nói một cách không chính thức, đó là tạo ra một trường chứa trường đã cho).
Việc tạo ra các trường $F_{1}, F_{2}, \ldots$ song hành với việc chọn các số $c_{0}, c_{1}, \ldots$ nhằm tạo ra một trường chứa một số dựng được cần được thực hiện một cách có chủ đích. Chẳng hạn nếu cứ chọn $c_{n} = 0$ hay $1$ thì các trường trên chỉ là trường số hữu tỉ, chúng ta sẽ mãi giậm chân tại chỗ và không bao giờ với tới con số $\sqrt{2}$, chứ chưa nói gì đến những biểu thức dài hơn như là $\sqrt{2} + \sqrt{3} + \sqrt{5 + \sqrt{7}}$.
(Bổ sung theo gợi ý từ anh @perfectstrong) Mình muốn làm rõ ghi chú ở sau phát biểu Mệnh đề 3. Mục tiêu của mình là chứng minh rằng có thể xây dựng được các trường liên tiếp sao cho có một trường trong dãy chứa một số dựng được cho trước. Mình nhận ra rằng mình cần phải chứng minh điều đó bằng hồi quy, bởi vì sự kết hợp của các phép toán với nhau rất hỗn loạn nhưng biểu thức luôn có khởi đầu đơn giản, ngắn gọn. Nếu chỉ chứng minh cho một số thì khi đến bước quy nạp, số dựng được $c$ (có không quá $(n+1)$ lần thực hiện phép toán) có phép toán cuối cùng là phép cộng chẳng hạn, thì mình viết $c = a + b$. Theo giả thiết quy nạp thì $a$ thuộc một trường (ứng với một dãy số khi thiết lập trường), $b$ cũng thuộc một trường (ứng với một dãy số khi thiết lập trường). Để mà kết hợp $a$ và $b$ và cho ra một trường chứa $c$, mình thấy quá xa vời, bởi vì $a$ và $b$ không nhất thiết cùng một trường (với cùng dãy số khi thiết lập trường). Thế nên mình bổ sung, để cho mệnh đề gồm hai số dựng được, rồi ba, rồi cho số lượng hữu hạn tùy ý - Có thêm những thay đổi này vì mình thấy sự xuất hiện của số 2 hay là số 3 thật là kỳ quặc, chi bằng tổng quát hóa.
Biểu thức $a + b\sqrt{c}$ có dáng dấp của phương trình Pell $x^{2} - d{y}^{2} = 1$. Lịch sử và phương pháp giải phương trình kiểu này có phần trình bày tương đối chi tiết và sâu sắc trong cùng cuốn sách Mathematics and Its History. Mình nghĩ cuốn sách cũng là một tư liệu hay cho những người yêu thích Toán, ngay cả khi không học ngành Toán.
5. Lời kết
Việc học từ các bài toán dựng hình là ý nghĩa với những ai muốn hiểu các đối tượng hình học trong hình học Euclid. Thông qua việc dựng hình, người học được vận dụng các kết quả đã biết, nhìn nhận mối liên kết giữa các đối tượng. Thật đáng buồn rằng nội dung dựng hình không còn được dạy chính thức.
Nếu chúng ta chỉ làm những thứ chúng ta biết, nói riêng là học hình học nhưng chỉ cần biết hình học chẳng hạn thì phần kiến thức đó cũng "đóng" như một trường vậy. Riêng trong trường hợp dựng hình này, bạn đọc đã thấy có những thứ nằm ngoài kiến thức của hình học phẳng, và nếu không vượt ra khuôn khổ của nó thì chưa chắc bài toán dựng hình Hy Lạp cổ đại kia đã có câu trả lời thỏa đáng.
Mình cảm thấy khó có thể nói điều sau mà không mang âm hưởng áp đặt: Để đi xa trong việc học Toán, hãy bước ra khỏi hình học phẳng, bước ra khỏi Olympic.
Cuối cùng, file PDF đính kèm là cuốn sách Mathematics and Its History mà mình tải về từ Z-Library (file có kích thước lớn hơn 1MB nên mình không upload lên được).
Bài viết đã được chỉnh sửa nội dung bởi manguish: 10-07-2023 - 16:32
Chỉnh LaTeX (có một công thức không hiển thị)