Chủ đề này có 159 trả lời

[perfectstrong]

Bài này có thể dùng đường thẳng Steiner anh à.Cũng khá đơn giản.

Em post lên đi, coi như là lời giải của anh là lời giải 2

[nguyenthehoan]

Em post lên đi, coi như là lời giải của anh là lời giải 2

Vâng.Dễ thấy gọi là đối xứng của $DE$ qua các cạnh của tam giác $XYZ$ chính là đối xứng của $DE$ qua các cạnh tam giác $ABC$.

 

Vì trực tâm tam giác $XYZ$ thuộc $DE$ nên đối xứng của $DE$ qua các cạnh tam giác $XYZ$ đồng quy.

 

Hay đối xứng của $DE$ qua các cạnh tam giác $ABC$ đồng quy.Suy ra $DE$ đi qua trực tâm tam giác $ABC$.

 

P/s:Lúc nghĩ ra bài này em cũng đi theo hướng của anh.Không ngờ lại có cách đơn giản hơn chỉ dùng đường thẳng Steiner

[nguyenthehoan]

Lâu lâu ko làm bất đẳng thức hình...

 

$\boxed{\text{Bài toán 20}}$ Cho $\Delta ABC$ đều cạnh bằng $\sqrt{3}$.$M$ là điểm bất kì di động

 

trong mặt phẳng tam giác.

 

Chứng minh rằng:$MA^{2}+MB^{2}+MC^{2}\leq MA^{2}.MB^{2}+MB^{2}.MC^{2}+MC^{2}.MA^{2}$

 

$\boxed{\text{Bài toán 21}}$ Với $P$ là điểm bất kì chạy trong mặt phẳng chứa $\Delta ABC$,Tìm vị trí của

 

$P$ để biểu thức 

 

$P=PA.PB+PB.PC+PC.PA$ đạt GTNN.Tính giá trị nhỏ nhất đó.

 

P/S:Hai bài khá dễ...Cái hay là tổng quát chúng

Giải quyết luôn hai bài này vậy

 

**** Bài 20: Ta có bổ đề: Cho tam giác $ABC$ với ba cạnh $a,b,c$.$M$ là một điểm bất kì trong mặt phẳng tam giác.

 

Khi đó với $x,y,z$ dương thì:

 

$(x+y+z)(xMA^{2}+yMB^{2}+zMC^{2})\geq a^{2}yz+b^{2}zx+c^{2}xy$  (***)

 

Bổ đề này đã được chứng minh tại đây:http://diendantoanho...fracb2yfracc2z/

 

Áp dụng:Cho $x=\frac{MB.MC}{MA},y=\frac{MC.MA}{MB},z=\frac{MA.MB}{MC}$

 

Ta có ngay điều phải chứng minh.Đẳng thức xảy ra khi $M$ là tâm tam giác $ABC$.

 

**** Bài 21:Ta cũng cần có một bổ đề (Từng là đề thi TST của trung quốc).

 

Cho tam giác $ABC$.$P$ là một điểm bất kì.Khi đó ta có 

 

$\sum \frac{PC.PB}{AB.AC}\geq 1$.Đẳng thức xảy ra khi $P$ trùng ba đỉnh hoặc trực tâm tam giác.

 

Áp dụng:Giả sử $BC\geq CA\geq AB$.Suy ra $BC.CA\geq BC.AB\geq AC.AB$

 

Nên $1\leq \sum \frac{PB.PC}{AB.AC}\leq \frac{\sum PB.PC}{AB.AC}$.

 

Vậy $\sum PA.PB\geq AB.AC$.Đẳng thức khi $P$ trùng $A$.

 

Chứng minh bổ đề:(China 98): Áp dụng trực tiếp bổ đề (***) với 

 

$x=\frac{PB.PC}{AB.AC},y=\frac{PC.PA}{BC.BA},z=\frac{PA.PB}{CA.CB}$ ta có

 

$\sum \frac{PA.PB}{CA.CB}\sum \frac{PC^{2}PA.PB}{CA.CB}\geq \sum \frac{PC^{2}PA.PB}{CA.CB}$

 

Ta có ngay điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 27-05-2013 - 16:43

[perfectstrong]

Em bổ sung thêm chứng minh cái bổ đề bài 21 vào cho anh luôn nhé

[perfectstrong]

$\boxed{\text{Bài toán 27}}$ http://www.artofprob...opic.php?t=6453

Let $AD$ be the common chord of two circles $\Gamma_1$ and $\Gamma_2$.  A line through $D$ intersects $\Gamma_1$ at $B$ and $\Gamma_2$ at $C$.  Let $E$ be a point on the segment $AD$, different from $A$ and $D$. The line $CE$ intersects $\Gamma_1$ at $P$ and $Q$.  The line $BE$ intersects $\Gamma_2$ at $M$ and $N$.

(i) Prove that $P, Q, M, N$ lie on the circumference of a circle $\Gamma_3$.

(ii) If the centre of $\Gamma_3$ is $O$, prove that $OD$ is perpendicular to $BC$.

===========================

Gọi $AD$ là dây chung của 2 đường tròn $\Gamma_1$ và $\Gamma_2$. 1 đường thẳng qua $D$ cắt $\Gamma_1$ tại $B$ và $\Gamma_2$ tại $C$. Gọi $E$ là 1 điểm trên đoạn $AD$, khác $A$ và $D$. Đường thẳng $CE$ cắt $\Gamma_1$ tại $P$ và $Q$. Đường thẳng $BE$ cắt $\Gamma_2$ tại $M$ và $N$.

 

(i) Chứng minh rằng $P,Q,M,N$ cùng nằm trên đường tròn $\Gamma_3$.

 

(ii) Nếu tâm của $\Gamma_3$ is $O$, chứng minh rằng $OD$ vuông góc với $BC$.

 

 

======================================================

 

 

$\boxed{\text{Bài toán 27}}$ http://www.artofprob...opic.php?t=6265

Two circles $\gamma_1$ and $\gamma_2$ meet at $A$ and $B$. Let $r$ be a line through $B$ that meets $\gamma_1$ at $C$ and $\gamma_2$ at $D$, such that $B$ is between $C$ and $D$. Let $s$ be the line parallel to $AD$, which is tangent to $\gamma_1$ in $E$ and has the minimal distance from $AD$. $EA$ meets $\gamma_2$ in $F$, and let $t$ be the line through $F$ which is tangent to $\gamma_2$. Prove that:
a) $t \parallel AC$.
b) $r,s$ and $t$ are concurrent.

===========================

2 đường tròn $\gamma_1$ và $\gamma_2$ cắt nhau tại $A$ và $B$. Gọi $r$ là 1 đường thẳng qua $B$ cắt $\gamma_1$ tại $C$ và $\gamma_2$ tại $D$ sao cho $B$ nằm giữa $C$ và $D$. Gọi $s$ là đường thẳng song song với $AD$ mà tiếp xúc với $\gamma_1$ tại $E$, đồng thời có khoảng cách ngắn nhất tới $AD$. $EA$ cắt $\gamma_2$ tại $F$, và gọi $t$ là đường thẳng qua $F$ tiếp xúc $\gamma_2$. Chứng minh rằng:

a) $t \parallel AC$.

b) $r,s$ và $t$ đồng quy.

[nguyenthehoan]

$\boxed{\text{Bài toán 27}}$ http://www.artofprob...opic.php?t=6453

 

Let $AD$ be the common chord of two circles $\Gamma_1$ and $\Gamma_2$.  A line through $D$ intersects $\Gamma_1$ at $B$ and $\Gamma_2$ at $C$.  Let $E$ be a point on the segment $AD$, different from $A$ and $D$. The line $CE$ intersects $\Gamma_1$ at $P$ and $Q$.  The line $BE$ intersects $\Gamma_2$ at $M$ and $N$.

(i) Prove that $P, Q, M, N$ lie on the circumference of a circle $\Gamma_3$.

(ii) If the centre of $\Gamma_3$ is $O$, prove that $OD$ is perpendicular to $BC$.

===========================

Gọi $AD$ là dây chung của 2 đường tròn $\Gamma_1$ và $\Gamma_2$. 1 đường thẳng qua $D$ cắt $\Gamma_1$ tại $B$ và $\Gamma_2$ tại $C$. Gọi $E$ là 1 điểm trên đoạn $AD$, khác $A$ và $D$. Đường thẳng $CE$ cắt $\Gamma_1$ tại $P$ và $Q$. Đường thẳng $BE$ cắt $\Gamma_2$ tại $M$ và $N$.

 

(i) Chứng minh rằng $P,Q,M,N$ cùng nằm trên đường tròn $\Gamma_3$.

 

(ii) Nếu tâm của $\Gamma_3$ is $O$, chứng minh rằng $OD$ vuông góc với $BC$.

 

 

======================================================

 

 

$\boxed{\text{Bài toán 28}}$ http://www.artofprob...opic.php?t=6265

 

Two circles $\gamma_1$ and $\gamma_2$ meet at $A$ and $B$. Let $r$ be a line through $B$ that meets $\gamma_1$ at $C$ and $\gamma_2$ at $D$, such that $B$ is between $C$ and $D$. Let $s$ be the line parallel to $AD$, which is tangent to $\gamma_1$ in $E$ and has the minimal distance from $AD$. $EA$ meets $\gamma_2$ in $F$, and let $t$ be the line through $F$ which is tangent to $\gamma_2$. Prove that:
a) $t \parallel AC$.
b) $r,s$ and $t$ are concurrent.

===========================

2 đường tròn $\gamma_1$ và $\gamma_2$ cắt nhau tại $A$ và $B$. Gọi $r$ là 1 đường thẳng qua $B$ cắt $\gamma_1$ tại $C$ và $\gamma_2$ tại $D$ sao cho $B$ nằm giữa $C$ và $D$. Gọi $s$ là đường thẳng song song với $AD$ mà tiếp xúc với $\gamma_1$ tại $E$, đồng thời có khoảng cách ngắn nhất tới $AD$. $EA$ cắt $\gamma_2$ tại $F$, và gọi $t$ là đường thẳng qua $F$ tiếp xúc $\gamma_2$. Chứng minh rằng:

a) $t \parallel AC$.

b) $r,s$ và $t$ đồng quy.

Bài giải:

 

Bài toán 27:

 

Gọi $I$ và $J$ thứ tự là tâm hai đường tròn.

 

Gọi $X$ và $Y$ là trung điểm của $PQ$ và $MN$.Vẽ $IZ$ và $JT$ vuông góc $BC$.

 

a) Ta có $\overline{EM}.\overline{EN}=\overline{EA}.\overline{ED}=\overline{EP}.\overline{EQ}$

 

Nên $M,N,P,Q$ cùng thuộc một đường tròn.

 

b)Nếu $O$ là tâm đường tròn đi qua $M,N,P,Q$ thì $XO\perp PQ,YO\perp MN$

 

Vậy để chứng minh $DO\perp BC$ ta phải chứng minh hai tam giác $DXY$ và $EBC$ trực giao.

 

Xét biểu thức $P=DB^{2}-DC^{2}+XC^{2}-XE^{2}+YE^{2}-YB^{2}$

 

Ta có $XC^{2}-XE^{2}=IC^{2}-IE^{2},YE^{2}-YB^{2}=JE^{2}-JB^{2}$ nên 

 

$P=DB^{2}-DC^{2}+IC^{2}-JB^{2}+JE^{2}-IE^{2}$

 

$=DB^{2}-DC^{2}+IC^{2}-JB^{2}+JD^{2}-ID^{2}$

 

$=DB^{2}-DC^{2}+IZ^{2}+ZC^{2}-JT^{2}-TB^{2}+JT^{2}+TD^{2}-IZ^{2}-DZ^{2}=0$

 

Do đó ta có DPCM.

 

Bài toán 28:

 

 

 

Gọi $P$ là giao điểm của $t$ và $r$.$O,I$ là tâm hai đường tròn.

 

a)Ta có $\widehat{AFP}=\widehat{AFD}+\widehat{DAE}=\widehat{ABE}+\frac{1}{2}\widehat{AID}=\widehat{ABE}+\frac{1}{2}\widehat{AOC}=\widehat{CBE}=\widehat{FAx}$

 

Với $Ax$ là tia đối của $AC$.

 

Vậy $PF//AC$ hay $t//AC$.DPCM.

 

b)Ta phải chứng minh $PE$ là tiếp tuyến của $(O)$.

 

Thật vậy:$\widehat{FPB}=\widehat{AEB}$ (cùng bù $\widehat{ACB}$)

 

Nên $FPBE$ nội tiếp.Suy ra $\widehat{PEF}=\widehat{PBF}=\widehat{DBF}=\widehat{DAF}$

 

Suy ra $EP//AD$ hay $EP\equiv t$

 

Vậy $r,t,s$ đồng quy tại $P$.DPCM.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 30-05-2013 - 15:59

[perfectstrong]

Bài 27b: Cách khác: (Theo ML)

 It is sufficient to prove that $ OB^2-OC^2=DB^2-DC^2$.
  We have\[
\begin{array}{rcl}
 OB^2  - OC^2  &=& P_{B/\left( {\Gamma _3 } \right)}  - P_{C/\left( {\Gamma _3 } \right)}  \\
  &=& \overline {BM} .\overline {BN}  - \overline {CP} .\overline {CQ}  \\
  &=& \overline {BD} .\overline {BC}  - \overline {CD} .\overline {CB}  \\
  &=& \left( {\overline {BD}  - \overline {CD} } \right)\left( {\overline {BD}  + \overline {CD} } \right) \\
  &=& BD^2  - CD^2  \\
 \end{array}
\]

=========================================

Ta chỉ cần chứng minh $ OB^2-OC^2=DB^2-DC^2$.

Ta có\[
\begin{array}{rcl}
 OB^2  - OC^2  &=& P_{B/\left( {\Gamma _3 } \right)}  - P_{C/\left( {\Gamma _3 } \right)}  \\
  &=& \overline {BM} .\overline {BN}  - \overline {CP} .\overline {CQ}  \\
  &=& \overline {BD} .\overline {BC}  - \overline {CD} .\overline {CB}  \\
  &=& \left( {\overline {BD}  - \overline {CD} } \right)\left( {\overline {BD}  + \overline {CD} } \right) \\
  &=& BD^2  - CD^2  \\
 \end{array}
\]

Bài 28b: Một vài hướng làm khác.

Cách 2:

Assume $R=r\cap AE,\, T=r\cap t,\, S=r\cap s$. We have to show that $T\equiv S$. We have $\frac {RD}{RS}=\frac {RA}{RE},\, \frac {RC}{RT}=\frac {RA}{RF}$. We thus need $\frac{RD}{RC}=\frac {RF}{RE}$. This is true because the lines $EC, FD$ are parallel (because $\angle AEC=\angle AFD$)

=====================================

Giả sử rằng $R=r \cap AE, T=r \cap t, S=r\cap s$. Ta sẽ chứng minh $T \equiv S$. Ta có $\frac {RD}{RS}=\frac {RA}{RE},\, \frac {RC}{RT}=\frac {RA}{RF}$. Ta chỉ cần chứng minh $\frac{RD}{RC}=\frac {RF}{RE}$. Điều này đúng bởi $EC,FD$ song song (do $\angle AEC=\angle AFD$).

 

 

Cách 3:

$BE$ intersected $(\gamma_2)$ at $X$.
Appliying the Reim's theorem, $FX\parallel s$.
$TF$ is the tangent to $(\gamma_2)$ at $F$.
According to a special case of Pascal's theorem for $FADBXF$, we are done.

=====================================

$BE$ cắt $(\gamma_2)$ tại $X$.

Áp dụng định lý Reim, ta có $FX \parallel s$.

$TF$ tiếp xúc $(\gamma_2)$ tại $F$.

Theo dạng đặc biệt của định lý Pascal cho $FADBXF$, ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 30-05-2013 - 10:16

[nguyenthehoan]

$\boxed{\text{Bài toán 29}}$ Cho tam giác $ABC$.Đường tròn nội tiếp $(I)$ tiếp xúa $BC,CA,AB$ lần lượt tại

 

$A_{1},B_{1},C_{1}$.Gọi $X$ là một điểm nằm trong tam giác $ABC$.$A_{2},B_{2},C_{2}$ thứ tự là các

 

giao điểm của $A_{1}X$ với $B_{1}C_{1}$,$B_{1}X$ với $C_{1}A_{1}$,$C_{1}X$ với

 

$A_{1}B_{1}$.$A_{3},B_{3},C_{3}$ là giao điểm của $A_{1}X,B_{1}X,C_{1}X$ với $(I)$.

 

a)Chứng minh rằng $AA_{2},BB_{2},CC_{2}$ đồng quy tại $P$.

 

b)Chứng minh rằng $AA_{3},BB_{3},CC_{3}$ đồng quy tại $Q$.

 

c)Chứng minh rằng $P,Q,X$ thẳng hàng.

 

Mathlinks:http://www.artofprob...p?f=46&t=515890

 

Let $I$ be incentre of incircle of triangle $ABC$.The circle $(I)$ tangents to the side $BC,CA,AB$ at 

 

$A_{1},B_{1},C_{1}$,respectively.Let $X$ be a point inside triangle $ABC$.$A_{2},B_{2},C_{2}$ 

 

be the intersections of $A_{1}X,B_{1}X,C_{1}X$ with the side $B_{1}C_{1},C_{1}A_{1},A_{1}B_{1}$.

 

$A_{1}X,B_{1}X,C_{1}X$ intersect the circle $(I)$ at the second points $A_{3},B_{3},C_{3}$.

 

a)Prove that $AA_{2},BB_{2},CC_{2}$ are concurrent at $P$.

 

b)Prove that $AA_{3},BB_{3},CC_{3}$ are concurrent at $Q$.

 

c)Prove that $P,Q,X$ are collinear.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 30-05-2013 - 10:40

[perfectstrong]

Bài 29: câu a đúng theo bài 4 do $AA_1,BB_1,CC_1$ đồng quy

[nguyenthehoan]

Bài 29: câu a đúng theo bài 4 do $AA_1,BB_1,CC_1$ đồng quy

Thực chất bài toán chỉ có câu c).Nhưng em tách thành ba ý cho nó chi tiết

[nguyenthehoan]

Lời giải Bài toán 29:

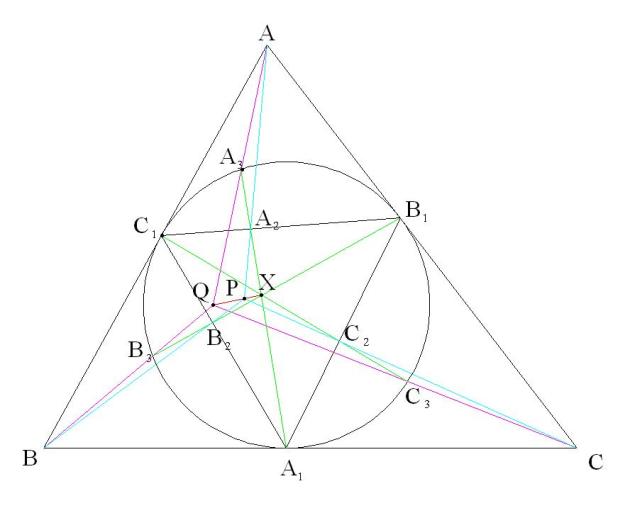
a)Bài 4.

 

b)Áp dụng định lí sin ta có:

 

$\frac{\sin \widehat{A_{3}AB_{1}}}{\sin \widehat{A_{3}B_{1}A}}=\frac{A_{3}B_{1}}{A_{3}A}$

 

Làm tương tự với tam giác $AA_{3}C_{1}$ rồi chia hai vế ta có 

 

$\frac{\sin \widehat{A_{3}AB_{1}}}{\sin \widehat{A_{3}AC{1}}}.\frac{\sin \widehat{A_{3}C_{1}A}}{\sin \widehat{A_{3}B_{1}A}}=\frac{A_{3}B_{1}}{A_{3}C_{1}}$

 

Hay: $\frac{\sin \widehat{A_{3}AB_{1}}}{\sin \widehat{A_{3}AC{1}}}.=\frac{A_{3}B_{1}}{A_{3}C_{1}}.\frac{\sin \widehat{A_{3}B_{1}A}}{\sin \widehat{A_{3}B_{1}A}}$

 

Lại có $\frac{A_{3}B_{1}}{A_{3}C_{1}}=\frac{\sin \widehat{A_{3}A_{1}B_{1}}}{\sin \widehat {A_{3}A_{1}C_{1}}}$

 

Suy ra $\frac{\sin \widehat{A_{3}AB_{1}}}{\sin \widehat{A_{3}AB_{1}}}=(\frac{\sin \widehat{A_{3}A_{1}B_{1}}}{\sin \widehat{A_{3}A_{1}C_{1}}})^{2}$

 

Xây dựng tương tự hai tỉ số nữa rồi nhân vào và sử dụng định lí XEeva dạng $sin$ ta có DPCM.

 

c)Áp dụng định lí Pascan ta có ngay tiếp tuyến tại $C_{1}$,$A_{3}B_{3}$ và $A_{2}B_{2}$ đồng 

 

quy tại $N$.

 

Hay $AB,A_{2}B_{2},A_{3}B_{3}$ đồng quy.

 

Áp dụng định lí Desargues ta có ngay $P,Q,X$ thẳng hàng.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 31-05-2013 - 16:21

[perfectstrong]

$\boxed{\text{Bài toán 30}}$ http://www.artofprob...opic.php?t=6088

$ABC$ is a triangle. $M$ is on $AB$ and $N$ is on $AC$ which satifies $MN\parallel BC$. Let $P$ be the midpoint of $BC$. Let $MP$ and $BN$ intersect at $X$. Let $Y$ be on $AC$ that $XY\perp AC$. Prove: $\widehat{MYX}=\widehat{PYX}$

 

===========================

 

Cho tam giác $ABC$. $M$ trên $AB$ và $N$ trên $AC$ sao cho $MN\parallel BC$. Gọi $P$ là trung điểm $BC$. $MP$ cắt $BN$ tại $X$. Lấy $Y$ trên $AC$ sao cho $XY \perp AC$. Chứng minh rằng: $\widehat{MYX}=\widehat{PYX}$

[nguyenthehoan]

$\boxed{\text{Bài toán 30}}$ http://www.artofprob...opic.php?t=6088

$ABC$ is a triangle. $M$ is on $AB$ and $N$ is on $AC$ which satifies $MN\parallel BC$. Let $P$ be the midpoint of $BC$. Let $MP$ and $BN$ intersect at $X$. Let $Y$ be on $AC$ that $XY\perp AC$. Prove: $\widehat{MYX}=\widehat{PYX}$

 

===========================

 

Cho tam giác $ABC$. $M$ trên $AB$ và $N$ trên $AC$ sao cho $MN\parallel BC$. Gọi $P$ là trung điểm $BC$. $MP$ cắt $BN$ tại $X$. Lấy $Y$ trên $AC$ sao cho $XY \perp AC$. Chứng minh rằng: $\widehat{MYX}=\widehat{PYX}$

Lời giải:

 

Để ý rằng $XY\perp YC$ nên để chứng minh $\widehat{MYX}=\widehat{PYX}$,ý tưởng tự nhiên ta

 

sẽ nghĩ tới là hàng điểm điều hòa.Cụ thể ta sẽ chứng minh: $Y(YM,YP,YX,YC)=-1$

 

Gọi $K$ là giao điểm của $MP$ với $AC$.Nhận thấy:

 

$MN//BC$ và $BC$ cắt $NB,NP,NC$ thỏa mãn $PB=PC$ nên ta có ngay: $N(NM,NP,NX,NC)=-1$ 

 

Hay $(MP,XK)=-1$.

 

Vậy $Y(YM,YP,YX,YC)=-1$.Hay ta có điều phải chứng minh.

 

Mở rộng Ta có bài toán tương tự sau:

 

(30.1) Cho tam giác $ABC$.$D,E,F$ thuộc các cạnh $AB,BC,CA$ thỏa mãn $AD,BE,CF$ đồng quy.

 

Gọi $X$ là hình chiếu của $D$ lên $EF$.Khi đó ta có $\widehat{BXD}=\widehat{CXD}$.

 

Làm xong 30,mình có một bài toán thế này.(cũng khá dễ thôi )

 

(30.2)Cho tam giác $ABC$.Điểm $M,N$ thứ tự thuộc các cạnh $AB,AC$ thỏa mãn $AN^{2}=AM.AB$

 

Qua $A$ vẽ tiếp tuyến thứ hai $AK$ đến $(BMN)$.Trên cung $NB$ không chứa $M,K$ của

 

$(BMN)$ lấy điểm $P$ thỏa mãn $\frac{PN}{PB}=2.\frac{KB}{KN}$.Gọi $E$ là giao điểm của $NP$ 

 

với $BC$.$ME$ cắt $NB$ tại $F$.Vẽ $FX\perp AC$.($X\in AC$).Chứng minh rằng:

 

$\widehat{MXF}=\widehat{EXF}$

[perfectstrong]

$\boxed{\text{Bài toán 31}}$ http://www.artofprob...opic.php?t=6076

Let $ ABC$ be a non-equilateral triangle. For a point $ P$ in the plane of $ ABC$, we denote by $ A^{\prime}$, $ B^{\prime}$, $ C^{\prime}$ the intersections of $ PA$, $ PB$, $ PC$ with the circumcircle of triangle $ ABC$. Show that there are exactly two positions of $ P$ for which triangle $ A^{\prime}B^{\prime}C^{\prime}$ is equilateral, and show that the line determined by them contains the circumcenter of $ ABC$.

 

===========================

Cho $ABC$ là 1 tam giác không đều. Với mỗi điểm $P$ trong mặt phẳng $ABC$, gọi $A',B',C'$ là những giao điểm của $PA,PB,PC$ và đường tròn ngoại tiếp $ABC$ tương ứng. Chứng minh rằng tồn tại đúng 2 vị trí của $P$ để $\triangle A'B'C'$ đều, và hơn nữa, đường thẳng đi qua 2 điểm đó chứa tâm đường tròn ngoại tiếp của $ABC$.

[nguyenthehoan]

$\boxed{\text{Bài toán 31}}$ http://www.artofprob...opic.php?t=6076

Let $ ABC$ be a non-equilateral triangle. For a point $ P$ in the plane of $ ABC$, we denote by $ A^{\prime}$, $ B^{\prime}$, $ C^{\prime}$ the intersections of $ PA$, $ PB$, $ PC$ with the circumcircle of triangle $ ABC$. Show that there are exactly two positions of $ P$ for which triangle $ A^{\prime}B^{\prime}C^{\prime}$ is equilateral, and show that the line determined by them contains the circumcenter of $ ABC$.

 

===========================

Cho $ABC$ là 1 tam giác không đều. Với mỗi điểm $P$ trong mặt phẳng $ABC$, gọi $A',B',C'$ là những giao điểm của $PA,PB,PC$ và đường tròn ngoại tiếp $ABC$ tương ứng. Chứng minh rằng tồn tại đúng 2 vị trí của $P$ để $\triangle A'B'C'$ đều, và hơn nữa, đường thẳng đi qua 2 điểm đó chứa tâm đường tròn ngoại tiếp của $ABC$.

Ta nhắc lại ba bổ đề quen thuộc sau:

 

1)Cho tam giác $ABC$ không đều.Phân giác trong và ngoài góc $A$ cắt $BC$ tại $X,Y$.Gọi $(\omega _{a})$

 

là đường tròn đường kính $XY$.Xác định tương tự các đường tròn $(\omega _{b}),(\omega _{c})$.

 

Khi đó các đường tròn $(\omega _{a}),(\omega _{b}),(\omega _{c})$ cùng đi qua hai điểm $D,E$                    

 

 2)Đường thẳng $DE$ đi qua tâm ngoại tiếp tam giác $ABC$.

 

3)Cho tam giác $ABC$ và 1 điểm $P$.$A',B',C'$ là giao của $PA,PB,PC$ với $(ACB)$.$D,E,F$ là

 

hình chiếu của $P$ lên $BC,CA,AB$.Khi đó hai tam giác $A'B'C'$ và $DEF$ đồng dạng.

 

Áp dụng vào bài toán:

 

Giả sử điểm $P$ thỏa mãn bài toán:.Theo bổ đề 3) thì tam giác $DEF$ đều.

 

Ta có $\frac{PC}{PB}=\frac{\sin{(PB,BD)}}{\sin{(CD,CP)}}=\frac{\sin{(PE,ED)}}{\sin{(ED,EP)}}$

 

Mặt khác áp dụng định lí Sin cho tam giác $PED$ và $PFD$ và chú ý $ED=FD$ ta có.

 

$\frac{\sin{(PE,ED)}}{\sin{(ED,EP)}}=\frac{\sin{(PD,PF)}}{\sin{(PE,PD)}}=\frac{\sin{(BF,BD)}}{\sin{(CD,CE)}}=\frac{AC}{AB}$

 

Vậy $\frac{PC}{PB}=\frac{AC}{AB}$.Hay $P$ nằm trên đường tròn Apollonius tỉ số $\frac{AC}{AB}$

 

dựng trên $BC$,Hay chính là đường tròn $\omega _{a}$ trong bổ đề 1.

 

Tương tự suy ra $P$ là giao điểm của 3 đường tròn $\omega _{a},\omega _{b},\omega _{c}$.

 

Do 3 đường tròn này cắt nhau tại 2 điểm và đường thẳng nối hai điểm này đi qua $O$ theo bổ đề 2 

 

nên ta có ngay DPCM.

 

P/S:Mở rộng bổ đề 1 và 2

 

(31.1)Cho tam giác $ABC$.Các điểm $A',B',C'$ thuộc $BC,CA,BA$ sao cho $AA',BB',CC'$ đồng 

 

quy.$A"$ là giao điểm của $BC$ với $B'C'$.Định nghĩa tương tự các điểm $B",C"$.Khi đó các

 

đường tròn đường kính $A'A",B'B",C'C"$ chung trục đẳng phương $\Delta$ và $\Delta$ đi qua tâm

 

ngoại tiếp tam giác $ABC$.

[perfectstrong]

3 bổ đề mà nguyenthehoan dùng, đều là về điểm isodynamic. Tính chất của nó, mọi người có thể xem thêm trong này

 Isodynamic_moon_c.pdf   261.83K   1713 Số lần tải

và đây

http://en.wikipedia....sodynamic_point

[perfectstrong]

$\boxed{\text{Bài toán 32}}$ http://www.artofprob...opic.php?t=5787

 

Given three fixed pairwisely distinct points $A$, $B$, $C$ lying on one straight line in this order. Let $G$ be a circle passing through $A$ and $C$ whose center does not lie on the line $AC$. The tangents to $G$ at $A$ and $C$ intersect each other at a point $P$. The segment $PB$ meets the circle $G$ at $Q$.

Show that the point of intersection of the angle bisector of the angle $AQC$ with the line $AC$ does not depend on the choice of the circle $G$.

 

===========================

 

Cho trước 3 điểm đôi một phân biệt $A,B,C$ cùng nằm trên 1 đường thẳng theo thứ tự đó. Gọi $G$ là đường tròn qua $A,C$ mà có tâm không nằm trên đường thẳng $AC$. Tiếp tuyến tới $G$ tại $A,C$ cắt nhau tại $P$. Đoạn $PB$ cắt đường tròn $G$ tại $Q$.

 

Chứng minh rằng giao điểm của phân giác góc $AQC$ và đường thẳng $AC$ không phụ thuộc cách chọn $G$.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 04-06-2013 - 14:59

[nguyenthehoan]

$\boxed{\text{Bài toán 32}}$

Given three fixed pairwisely distinct points $A$, $B$, $C$ lying on one straight line in this order. Let $G$ be a circle passing through $A$ and $C$ whose center does not lie on the line $AC$. The tangents to $G$ at $A$ and $C$ intersect each other at a point $P$. The segment $PB$ meets the circle $G$ at $Q$.

Show that the point of intersection of the angle bisector of the angle $AQC$ with the line $AC$ does not depend on the choice of the circle $G$.

 

===========================

 

Cho trước 3 điểm đôi một phân biệt $A,B,C$ cùng nằm trên 1 đường thẳng theo thứ tự đó. Gọi $G$ là đường tròn qua $A,C$ mà có tâm không nằm trên đường thẳng $AC$. Tiếp tuyến tới $G$ tại $A,C$ cắt nhau tại $P$. Đoạn $PB$ cắt đường tròn $G$ tại $Q$.

 

Chứng minh rằng giao điểm của phân giác góc $AQC$ và đường thẳng $AC$ không phụ thuộc cách chọn $G$.

 

Bài toán là hệ quả trực tiếp của định lí về tứ giác điều hòa.

 

Theo một bài toán quen biết thì ta có ngay $QP$ là đường đối trung của tam giác $AQC$.

 

Do đó theo tính chất đường đối trung ta có ngay:

 

$\frac{QA}{QC}=(\frac{BA}{BC})^{2}$ không đổi.

 

Gọi $E$ là giao của phân giác góc $\widehat{AQC}$ tới $AC$ thì 

 

$\frac{EA}{EC}=\frac{QA}{QC}=(\frac{BA}{BC})^{2}$,do đó $E$ cố định.

 

Ta có DPCM.

[barcavodich]

Bạn chứng minh lại đường đối trung giùm với

Mình quên béng cách chứng minh rồi

[perfectstrong]

$\boxed{\text{Bài toán 33}}$ http://www.artofprob...opic.php?t=5959

 

Let $(O)$ be a fixed circle and $A, B$ be 2 fixed points lying on it. $C$ varies on $(O)$. Denote by $M, N$ respectively the intersections of the perpendicular bisectors of $CA$ and $CB$ and the bisector $CD$ of $ACB$. Let $K$ be the intersection of the lines through $M, N$ respectively parallel to $CA, CB$.

Prove that $CK$ always passes through a fixed point.

 

===========================

 

Cho $(O)$ là 1 đường tròn cố định và $A,B$ là 2 điểm cố định trên đó. $C$ di động trên $(O)$. Gọi $M,N$ lần lượt là giao điểm của trung trực $CA,CB$ với phân giác $CD$ của $ACB$. Gọi $K$ là giao điểm của đường thẳng qua $M,N$ thứ tự song song với $CA,CB$.

Chứng minh rằng $CK$ luôn qua 1 điểm cố định.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 04-06-2013 - 15:12