Chủ đề này có 159 trả lời

[nguyenthehoan]

$\boxed{\text{Bài toán 33}}$ http://www.artofprob...opic.php?t=5959

 

Let $(O)$ be a fixed circle and $A, B$ be 2 fixed points lying on it. $C$ varies on $(O)$. Denote by $M, N$ respectively the intersections of the perpendicular bisectors of $CA$ and $CB$ and the bisector $CD$ of $ACB$. Let $K$ be the intersection of the lines through $M, N$ respectively parallel to $CA, CB$.

Prove that $CK$ always passes through a fixed point.

 

===========================

 

Cho $(O)$ là 1 đường tròn cố định và $A,B$ là 2 điểm cố định trên đó. $C$ di động trên $(O)$. Gọi $M,N$ lần lượt là giao điểm của trung trực $CA,CB$ với phân giác $CD$ của $ACB$. Gọi $K$ là giao điểm của đường thẳng qua $M,N$ thứ tự song song với $CA,CB$.

Chứng minh rằng $CK$ luôn qua 1 điểm cố định.

Trước hết ta phát biểu và chứng minh bổ đề quen thuộc sau:

 

Cho $\Delta ABC$ và một điểm $P$.$I,J$ là hình chiếu của $P$ lên $AB,AC$.Nếu $\frac{PI}{PJ}=\frac{AB}{AC}$ thì $P$ nằm trên

 

đường đối trung đỉnh $A$ của $\Delta ABC$.

 

 

Chứng minh:Ta có $\frac{PI}{PJ}=\frac{\sin \widehat{PAB}}{\sin \widehat{PAC}}$

 

Gọi $R$ là giao điểm của $AP$ và $BC$.Áp dụng định lí Sin cho hai tam giác $RAB$ và $RAC$ ta có

 

$\frac{\sin \widehat{PAB}}{\sin \widehat{PAC}}=\frac{TB}{TC}.\frac{AC}{AB}$

 

Từ đó $\frac{RB}{RC}=(\frac{AB}{AC})^{2}$.Nên theo tính chất đường đối trung ta có ngay DPCM.

 

Áp dụng vào bài toán:Gọi $X,Y$ là trung điểm của $AB,AC$

 

 

Vẽ $KE\perp BA$ và $KF\perp AC$.Các tứ giác $KMXE$ và $KNYF$ là hình chữ nhật cho ta 

 

$KE=MX$ và $KF=MY$.Do đó $\frac{KE}{KF}=\frac{MX}{NY}=\frac{CX}{CY}=\frac{CA}{CB}$

 

(Do $CM$ là phân giác góc $\widehat{ACB}$)

 

Do đó theo bổ đề ta có ngay $CK$ là đường đối trung của tam giác $ABC$.Theo một tính chất

 

quen biết thì $CK$ đi qua giao điểm các tiếp tuyến tại $A,B$ của $(O)$ và ta có DPCM.

[perfectstrong]

Một nhận xét của darij grinberg trong bài toán 33 là

The barycentric coordinates of the point $K$ with respect to triangle $ABC$ are $\left( a^{2}:b^{2}:2ab-c^{2}\right) $.

Equivalently, its trilinear coordinates are $\left( ca:bc:2ab-c^{2}\right)$
 

===============================

Tọa độ tỉ cự của điểm $K$ đối với tam giác  $ABC$ là $\left( a^{2}:b^{2}:2ab-c^{2}\right) $.

 

Tương tự, tọa độ trilinear là $\left( ca:bc:2ab-c^{2}\right)$

 

 

**************************

Tham khảo về tọa độ trilinear: http://en.wikipedia....ear_coordinates

[perfectstrong]

$\boxed{\text{Bài toán 34}}$ http://www.artofprob...opic.php?t=5995

 

Let $A$ be a point outside the circle $(\gamma)$, and $AB$ and $AC$ be the two tangents from $A$ to this circle $(\gamma)$. Let $l$ be an arbitrary tangent to $(\gamma)$ that cuts $AB$ and $AC$ in $P$ and $Q$ respectively. A line through $P$ parallel to $AC$ cuts $BC$ in $R$.

Prove that while $l$ varies, $QR$ passes through a fixed point.

 

===========================

Cho $A$ là 1 điểm ngoài đường tròn $(\gamma)$, và $AB,AC$ là 2 tiếp tuyến từ $A$ tới đường tròn $(\gamma)$. Gọi $l$ là 1 tiếp tuyến bất kì của $(\gamma)$ cắt $AB,AC$ tại $P,Q$ tương ứng. 1 đường thẳng qua $P$ song song với $AC$ cắt $BC$ tại $R$.

Chứng minh rằng khi $l$ di động, $QR$ qua 1 điểm cố định.

[nguyenthehoan]

Tiếp tục:http://www.artofprob...hp?f=47&t=76947

_______________________________________

$\boxed{\text{Bài toán 35}}$ Let $ABC$ be a triangle for which $(a-b)(a-c)<0$.Denote the $D,E$ are the intersections of the line $IG$ with $AB$ and $AC$,where $I$ and $G$ are the incentre and centroid of triangle $ABC$,respectively.If the quadrilateral $BCED$ is cyclic,prove the inequality $\frac{1}{b}+\frac{1}{c}<\frac{2}{a}$

 

===================================================

 

Cho tam giác $ABC$ thỏa mãn $(a-b)(a-c)<0$ với $a,b,c$ là ba cạnh tam giác.Gọi $I,G$ thứ tự là tâm nội tiếp và trọng tâm tam giác.$D,E$ là giao điểm của đường thẳng $IG$ với các cạnh $AB$ và $AC$.Nếu tứ giác $BCED$ nội tiếp,hãy chứng minh bất đẳng thức sau: $\frac{1}{b}+\frac{1}{c}<\frac{2}{a}$

[nguyenthehoan]

Lời giải Bài toán 34

 

 

Ta sẽ chứng minh trong trường hợp tiếp tuyến $l$ cắt các cạnh $AB,AC$.Trường hợp còn lại chứng

 

minh tương tự.

 

Gọi $K$ là giao điểm của $QR$ với $AB$,ta sẽ chứng minh $K$ là điểm cố định.

 

Theo định lí Mêlêlauyt ta có:$\frac{KB}{KA}.\frac{QA}{QC}.\frac{RC}{RB}=1\Rightarrow \frac{KB}{KA}=\frac{QC}{QA}.\frac{PB}{PA}$

 

(Đã áp dụng định lí talet).

 

Gọi $X,Y$ là giao điểm của $BC$ với $OP,OQ$.Ta có $\widehat{POQ}=\frac{\widehat{COB}}{2}=\widehat{BOA}=\widehat{COA}$

 

Do đó $BPYO$ và $CQXO$ là các tứ giác nội tiếp.Từ đó $\Delta BPX\sim \Delta CYQ(gg)$ nên

 

$BP.CQ=BX.CY$.Lại có $\widehat{OXC}=\widehat{OQC}\Rightarrow \widehat{OXB}=\widehat{OQA}$

 

Và $\widehat{OBX}=\widehat{OAQ}\Rightarrow \Delta OXB\sim \Delta OQA$

 

Suy ra $\frac{BX}{AQ}=\frac{BO}{AO}$.Tương tự $\frac{CY}{AP}=\frac{CO}{AO}$.Suy ra 

 

$\frac{BX.CY}{AQ.AP}=(\frac{R}{AO})^{2}$.Hay $\frac{BP.CQ}{AQ.AP}=(\frac{R}{AO})^{2}$.

 

Vậy ta có $\frac{KB}{KA}=(\frac{R}{OA})^{2}$ nên $X$ cố định.Ta có DPCM.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 05-06-2013 - 08:09
Sửa tên điểm

[perfectstrong]

Bài 34: (mọi người check giúp luôn nhé )

Thêm 3 lời giải khác từ ML

Solution 2:

We will prove that the pole of $QR$ is on a fixed line. The pole of $QR$ is the intersection of the polars of $Q$ and $R$.

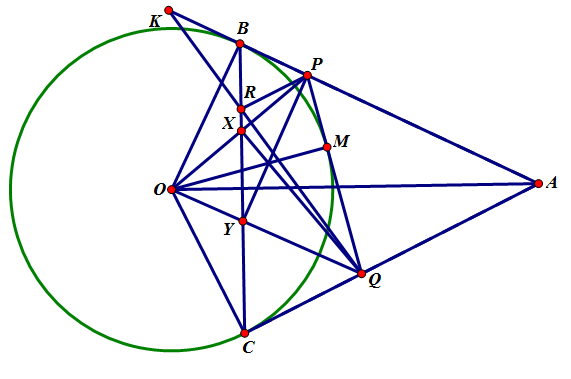
Let $l$ be tangent to $(\gamma)$ in $X$. So the polar of $Q$ is $XC$ . We name the line through $P$ parallel to $AC$: $d$.

So the polar of $R$ is the line through $A$ and the pole of $d$.

The pole of $d$ (which is $Y$) is on the diameter of $(\gamma)$ perpendicular to $d$ (which is the diameter through $C$ which we name $CD$) . It lies also on $BX$. So we have found $Y=(CD, BX)$. Let $Z$ be the intersection of $CX$ and $AY$( so $Z$ is the pole of $QR$).
Now to finish: its obvious that $Z$ is on $BD$ which is constant ( because $AY$ ,the polar of $R$, passes through $Z$ so the

polar of $Z$ passes through $R$ so $Z$ is on $BD$)

 

Lời giải 2:

Ta sẽ chứng minh cực của $QR$ nằm trên 1 đường thẳng cố định. Cực của $QR$ là giao điểm của đường đối cực ứng với $Q$ và $R$.

$l$ tiếp xúc $(\gamma)$ tại $X$. Do đó đường đối cực của $Q$ là $XC$. Ta gọi đường thẳng qua $P$ song song với $AC$ là $d$.

Do đó đường đối cực ứng với $R$ là đường thẳng qua $A$ và cực của $d$.

Cực của $d$ (gọi là $Y$) nằm trên đường kính của $(\gamma)$ sao cho đường kính đó vuông góc với $d$ (đó là đường kính qua $C$ mà ta gọi là $CD$). Nó cũng nằm trên $BX$. Do đó ta có $Y=CD \cap BX$. Gọi $Z$ là giao của $CX$ và $AY$ thì $Z$ là cực của $QR$.

Để hoàn tất: rõ ràng rằng $Z$ nằm trên $BD$ là cố định (vì $AY$, đường đối cực của $R$, đi qua $Z$ nên đường đối cực của $Z$ đi qua $R$, từ đó $Z$ nằm trên $BD$.).

===============================

Solution 3:

Suppose $T$ is intersection of $QR$ and $AB$ If the tangent from $T$ to circle (not $AB$ the other) is' not parallel to $AC$ by Brianchon theorem $PR$ , $AC$ and tangent from $T$ to circle are concurrent.
But $PR$ is parallel to $AC$ contradiction. So $T$ is constant.

 

Lời giải 3:

Giả sử rằng $T$ là giao điểm của $QR$ và $AB$. Nếu tiếp tuyến từ $T$ tới đường tròn (khác $AB$) không song song với $AC$ thì do định lý Brianchon, $PR,AC$ và tiếp tuyến từ $T$ đồng quy.

Nhưng $PR \parallel AC$: mâu thuẫn. Vậy $T$ cố định.

===============================

Solution 4:

We must show that the application from line $AC$ to line $BC$ which maps $Q\to R$ is a perspectivity. In order to do this we must show that it's a homographic (preserving the cross-ratio) transformation and it maps $C\to C$.

It's easy to see that it's homographic because it's the composition of $Q\to P$ (from line $AC$ to line $AB$; it's wel-known that this sort of transformation is homographic (even if $(\gamma)$ is a conic, not only a circle)) and $P\to R$ (from line $AB$ to line $BC$).

We must now show that $C\to C$. In this case $Q=C\Rightarrow l=AC\Rightarrow P=A\Rightarrow PR=AC\Rightarrow R=AC\cap BC=C$, Therefore, $QR$ always passes the center of that perspectivity and we're done.

 

Lời giải 4:

Ta phải chứng minh rằng ánh xạ từ đường thẳng $AC$ tới đường thẳng $BC$ mà biến $Q \to R$ là 1 phép chiếu xuyên tâm. Để chứng minh điều này, ta chỉ cần chứng minh đó là phép biến hình đơn ánh (bảo toàn tỉ số kép) và biến $C \to C$.

 

Dễ thấy đó là phép biến hình đơn ánh vì nó là tích ánh xạ của $Q \to P$ (từ đường thẳng $AC$ tới đường thẳng $AB$, đây là điều quen thuộc rằng những biến hình như vậy là đơn ánh (kể cả khi $(\gamma)$ là đường conic, không là hình tròn)) và $P \to R$ (từ đường thẳng $AB$ tới đường thẳng $BC$).

 

Ta chỉ cần chứng minh rằng $C \to C$. Khi $Q=C\Rightarrow l=AC\Rightarrow P=A\Rightarrow PR=AC\Rightarrow R=AC\cap BC=C$. Như vậy $QR$ luôn đi qua tâm chiếu biến đường thẳng $BC$ thành $AC$. Chứng minh hoàn tất.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 05-06-2013 - 09:06

[perfectstrong]

Bài 34: Anh/em/mình tìm được thêm 1 lời giải nữa

Lời giải 5:

Vẽ $l$ tiếp xúc $(\gamma)$ tại $E$. $O$ là tâm của $(\gamma)$. Dựng đường kính $CD$. Tiếp tuyến tại $D$ của $(O)$ cắt $AB$ tại $T$: cố định.

Ta sẽ chứng minh $Q,R,T$ thẳng hàng. Trước hết, ta chứng minh $RE$ đi qua $D$. Thật vậy:

Dễ thấy $\vartriangle PBR$ cân tại $P$ mà $PB=PE$ nên suy ra $PB=PR=PE$, tức $P$ là tâm đường tròn ngoại tiếp $\vartriangle BRE$. Do đó:

\[
\begin{array}{l}
  \Rightarrow \left( {EP;ER} \right) \equiv \frac{\pi }{2} + \frac{1}{2}\left( {PR;PE} \right) \equiv \frac{\pi }{2} + \left( {BR;BE} \right) \equiv \frac{\pi }{2} + \frac{1}{2}\left( {OC;OE} \right) \pmod {\pi }  \\
  \Rightarrow \left( {EP;ER} \right) \equiv \frac{\pi }{2} + \left( {OQ;OE} \right) \equiv \left( {QE;QO} \right)\pmod {\pi } \\
  \Rightarrow RE\parallel OQ \Rightarrow \left( {ER;EC} \right) \equiv \left( {QO;EC} \right) \equiv \frac{\pi }{2} \equiv \left( {ED;EC} \right)\pmod {\pi } \\
 \end{array}
\]

Từ đó ta có $E,R,D$ thẳng hàng. Nếu $EC \parallel BD \Rightarrow l \parallel AB$: mâu thuẫn nên $EC \cap BD=H$.

Đường đối cực của $T,Q$ đối với $(O)$ đi qua $H$ nên $TQ$ là đường đối cực của $H$.

Mặt khác, $HBD,HEC$ là 2 cát tuyến tới $(O)$ và $BC \cap ED=R \Rightarrow R \in TQ$ hay $QT$ luôn qua $R$ cố định.

[perfectstrong]

$\boxed{\text{Bài toán 36}}$ http://www.artofprob...opic.php?t=5189

 

Let $ABC$ be a triangle and $H$ it's orthocenter. We draw two lines through the point $H$ which are perpendicular to each other. The first line intersects the lines $BC, CA, AB$ at the points $A_{1}, B_{1}, C_{1}$, respectively; the second line intersects the lines $BC, CA, AB$ at the points $A_{2}, B_{2}, C_{2}$, respectively. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the midpoints of the segments $A_{1}A_{2}, B_{1}B_{2}, C_{1}C_{2}$, respectively.

 

Prove that these points $A^{\prime}, B^{\prime}, C^{\prime}$ lie on one line.

 

===============================

 

Cho $ABC$ là 1 tam giác có $H$ là trực tâm. Ta vẽ 2 đường thẳng qua $H$ vuông góc nhau. Đường thẳng thứ 1 cắt $BC,CA,AB$ tại $A_1,B_1,C_1$ tương ứng. Đường thẳng thứ 2 cắt $BC,CA,AB$ tại $A_2,B_2,C_2$ tương ứng. Gọi $A^{\prime}, B^{\prime}, C^{\prime}$ lần lượt là trung điểm $A_1A_2,B_1B_2,C_1C_2$.

 

Chứng minh rằng $A^{\prime}, B^{\prime}, C^{\prime}$ thẳng hàng.

[nguyenthehoan]

Lời giải bài toán 36:

Trước hết ta phát biểu và chứng minh một bổ đề:Cho tam giác $ABC$,trực tâm $H$.$AH,BH,CH$ cắt

$(ABC)$ tại $D,E,F$.Một đường thẳng qua $H$ cắt $BC,CA,AB$ tại $X,Z,Y$.Khi đó ta có $(HXD),(HEZ),(HFY)$ đồng quy tại 1 điểm trên $(ABC)$.

 

Chứng minh:Gọi $P$ là giao điểm của $(HYF)$ và $(HZE)$.Ta sẽ chứng minh $P\in (ABC)$.

 

Thật vậy:$(EP,PZ)=(EP,PH)+(PH,PF)=2\pi -(HZ,ZE)-(FY,YH)=2(\pi -(HZ,ZA)-(AY,YH))=2(ZA,AY)=2(CA,AB)$.

 

Từ đó suy ra $P$ thuộc $(ABC)$.Tương tự từ đó suy ra bổ đề trên.

 

Áp dụng bổ đề vào bài toán:

 

Ta dễ dàng có $H,A_{1},A_{2},D$ cùng thuộc đường tròn đường kính $A_{1}A_{2}$.

 

Tương tự ta và áp dụng bổ đề ta có ngay các đường tròn đường kính $A_{1}A_{2},B_{1}B_{2},C_{1}C_{2}$ cùng đi qua 2 điểm.

 

Từ đó suy $A',B',C'$ thẳng hàng.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 06-06-2013 - 20:57

[nguyenthehoan]

Mình có một mở rộng rất hay cho bài 36 như sau:

(36.1) Cho tam giác $ABC$ nhọn,$H$ là điểm bất kì trong tam giác.Gọi $D$ là đối xứng của $H$ qua $BC$,Và $X$ là giao điểm của $AH$ với $(ABC)$.Gọi $A_{1}$ và $A_{2}$ là giao điểm của các phân giác trong và ngoài góc $X$ của $\Delta HDX$ với $BC$.Đường thẳng $A_{1}H$ cắt $CA,AB$ tại $B_{1},C_{1}$.Đường thẳng $A_{2}H$ cắt $CA,AB$ tại $B_{2},C_{2}$.Gọi $A',B',C'$ thứ tự là trung điểm của $A_{1}A_{2},B_{1}B_{2},C_{1}C_{2}$.Chứng minh rằng $A',B',C'$ thẳng hàng.

 

Lang thang xem lại các bài toán cũ của VMF,phát hiện vài điều rất lí thú:

+)Đường thẳng $A'B'C'$ trong bài toán 36 chính là đường thẳng Droz-Farny

Một số bài toán liên quan:

(36.2) Cho $\Delta ABC$ và $d$ là đường thẳng đi qua trực tâm $H$.$d_{a}$ là đối xứng của $BC$ qua $d$.$d_{a}$ cắt đường thẳng qua $H$ song song $BC$ tại $A'$.Định nghĩa tương tự các điểm $B',C'$.Chứng minh rằng $A',B',C'$ thẳng hàng.

(36.2) Cho tam giác $ABC$ trực tâm $H$.$d$ và $d'$ là hai đường thẳng bất kì qua $H$.$d$ cắt $BC,CA,AB$ tại $A',B',C'$ và $D'$ cắt $BC,CA,AB$ tại $A",B",C"$.Gọi $O_{1},O_{2},O_{3}$ là tâm ngoại tiếp các tam giác $HA'A",HB'B",HC'C"$.$HO_{1},HO_{2},HO_{3}$ cắt $A'A",B'B",C'C"$ tại $M,N,P$.Chứng minh rằng $M,N,P$ thẳng hàng.

 

Một file mình kiếm đươc..(không nhiều lắm)

 Droz-farny line.pdf   25.63K   266 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 08-06-2013 - 11:41

[perfectstrong]

Một lời giải khác cũng khá hay trong bài 36 dựa trên nhận xét là các tứ giác toàn phần $ABCA_1B_1C_1,ABCA_2B_2C_2$ có cùng điểm Miquel.

Chứng minh:

Ta nhắc lại định lý Miquel cho tam giác:

 

Cho $\vartriangle ABC$ và 3 điểm $X,Y,Z$ thứ tự trên $BC,CA,AB$.

Khi đó, $(AYZ),(BXZ),(CXY)$ đồng quy.

============================

Gọi $H_a,H_b$ lần lượt là điểm đối xứng của $H$ qua $BC,CA$. Dễ thấy $H_a,H_b \in (ABC)$ và $A_1H_a,H_bB_1$ là các đường thẳng đối xứng của $d_1$ qua $BC,CA$ tương ứng.

Suy ra, theo định lý Collings, $A_1H_a\cap H_bB_1=K \in (ABC)$.

Áp dụng định lý Miquel cho $\triangle KA_1B_1$ với 3 điểm $H_a,H,H_b$ thì $(KH_aH_b),(A_1HH_a),(B_1H_bH)$ đồng quy tại điểm $M$. (*)

Chú ý do tính đối xứng nên $\widehat{A_2HA_1}=\widehat{A_2H_aA_1}=90^o \Rightarrow A_2 \in (A_1HH_a)$. Tương tự $B_2 \in (HB_1H_b)$.

Như vậy $M$ là giao điểm còn lại của $(A_1HA_2),(B_2HB_1)$. Do đó $M$ là điểm Miquel của tứ giác toàn phần $CB_1HA_2B_2A_1$.

Suy ra $M \in (CB_1A_1)$. Mà chú ý từ (*) nên $M \in (KH_aH_b)=(ABC)$.

Do đó $M$ là điểm Miquel của tứ giác toàn phần $ABCA_1B_1C_1$. Tương tự, $M$ cũng là điểm Miquel của tứ giác toàn phần $ABCA_2B_2C_2$.

3 đường tròn đường kính $A_1A_2,B_1B_2,C_1C_2$ cùng đi qua 2 điểm $M,H$ nên tâm của chúng thẳng hàng. Ta có đpcm.

[perfectstrong]

Tiếp tục:http://www.artofprob...hp?f=47&t=76947

_______________________________________

$\boxed{\text{Bài toán 35}}$ Let $ABC$ be a triangle for which $(a-b)(a-c)<0$.Denote the $D,E$ are the intersections of the line $IG$ with $AB$ and $AC$,where $I$ and $G$ are the incentre and centroid of triangle $ABC$,respectively.If the quadrilateral $BCED$ is cyclic,prove the inequality $\frac{1}{b}+\frac{1}{c}<\frac{2}{a}$

 

===================================================

 

Cho tam giác $ABC$ thỏa mãn $(a-b)(a-c)<0$ với $a,b,c$ là ba cạnh tam giác.Gọi $I,G$ thứ tự là tâm nội tiếp và trọng tâm tam giác.$D,E$ là giao điểm của đường thẳng $IG$ với các cạnh $AB$ và $AC$.Nếu tứ giác $BCED$ nội tiếp,hãy chứng minh bất đẳng thức sau: $\frac{1}{b}+\frac{1}{c}<\frac{2}{a}$

Lời giải:

Không mất tính tổng quát, giả sử $b \le c$. Từ giả thiết, ta có: $b<a<c \quad (*)$

Trên trục $BC$, chọn chiều trùng với $\overrightarrow{BC}$.

Vẽ $AI,AG$ cắt $BC$ tại $L,K$ tương ứng. Theo tính chất phân giác, ta có:

\[
\frac{{LC}}{{LB}} = \frac{b}{c} \Rightarrow \frac{{LC}}{{BC}} = \frac{b}{{b + c}} \Rightarrow LC = \frac{{ab}}{{b + c}} \Rightarrow LB = \frac{{ac}}{{b + c}}
\]
Vì $c>b>0$ nên \[
CL = \frac{{ab}}{{b + c}} < \frac{{ab}}{{2b}} = \frac{a}{2} = CK \Rightarrow L \in \left[ {CK} \right]
\]
Mặt khác:\[
\begin{array}{l}
 \frac{{IL}}{{IA}} = \frac{{CL}}{{CA}} = \frac{{BL}}{{BA}} = \frac{a}{{b + c}} \\
  \Rightarrow LK = CK - CL = \frac{a}{2} - \frac{{ab}}{{b + c}} = \frac{{a\left( {c - b} \right)}}{{2\left( {c + b} \right)}} \\
 \end{array}
\]
Giả sử $b+c=2a$ thì $\frac{{IL}}{{IA}} = \frac{a}{{b + c}} = \frac{1}{2} = \frac{{GK}}{{GA}} \Rightarrow IG\parallel BC$.

Điều này cho ta $BDEC$ là hình thang. Mà $BDEC$ là tứ giác nội tiếp nên $\widehat{DBC}=\widehat{ECB} \Rightarrow c=b$: trái với (*). Do đó $b+c \ne 2a$ và $IG \cap BC=M$.

Áp dụng định lý Menelaus cho $\triangle AKL$ với cát tuyến $GIM$

\[
\begin{array}{l}
 \frac{{\overline {MK} }}{{\overline {ML} }}.\frac{{\overline {IL} }}{{\overline {IA} }}.\frac{{\overline {GA} }}{{\overline {GK} }} = 1 \Rightarrow \frac{{\overline {MK} }}{{\overline {ML} }} = \frac{{\overline {IA} }}{{\overline {IL} }}.\frac{{\overline {GK} }}{{\overline {GA} }} = \left( { - \frac{{b + c}}{a}} \right).\left( { - \frac{1}{2}} \right) = \frac{{b + c}}{{2a}} \\
  \Rightarrow \frac{{\overline {MK} }}{{\overline {LK} }} = \frac{{b + c}}{{b + c - 2a}} \Rightarrow \overline {MK}  = \frac{{b + c}}{{b + c - 2a}}.\overline {LK}  = \frac{{b + c}}{{b + c - 2a}}.\left[ { - \frac{{a\left( {c - b} \right)}}{{2\left( {c + b} \right)}}} \right] = \frac{{a\left( {b - c} \right)}}{{2\left( {b + c - 2a} \right)}} \\
 \end{array}
\]
Từ đó:\[
\frac{{\overline {MB} }}{{\overline {MK} }} = 1 + \frac{{\overline {KB} }}{{\overline {MK} }} = 1 + \frac{{ - \frac{a}{2}}}{{\frac{{a\left( {b - c} \right)}}{{2\left( {b + c - 2a} \right)}}}} = \frac{{2\left( {c - a} \right)}}{{c - b}}
\]
Áp dụng định lý Menelaus cho $\triangle AKB$ với cát tuyến $DGM$

\[
\begin{array}{l}
 \frac{{\overline {DA} }}{{\overline {DB} }}.\frac{{\overline {MB} }}{{\overline {MK} }}.\frac{{\overline {GK} }}{{\overline {GA} }} = 1 \Rightarrow \frac{{\overline {DA} }}{{\overline {DB} }} = \frac{{\overline {MK} }}{{\overline {MB} }}.\frac{{\overline {GA} }}{{\overline {GK} }} = \frac{{c - b}}{{2\left( {c - a} \right)}}.\left( { - 2} \right) = \frac{{b - c}}{{c - a}} \\
  \Rightarrow \frac{{\overline {DA} }}{{\overline {BA} }} = \frac{{b - c}}{{b + a - 2c}} \Rightarrow \overline {AD} .\overline {AB}  = c^2 .\frac{{c - b}}{{2c - a - b}},\left( 1 \right) \\
 \end{array}
\]
Tương tự:\[
\overline {AE} .\overline {AC}  = b^2 .\frac{{c - b}}{{a + c - 2b}},\left( 2 \right)
\]
Từ (1),(2) và do $BDEC$ nội tiếp được nên \[
\begin{array}{l}
 c^2 .\frac{{c - b}}{{2c - a - b}} = b^2 .\frac{{c - b}}{{a + c - 2b}} \\
  \Leftrightarrow c^2 \left( {a + c - 2b} \right) = b^2 \left( {2c - a - b} \right) \\
  \Leftrightarrow a\left( {b^2  + c^2 } \right) + b^3  + c^3  - 2bc\left( {b + c} \right) = 0 \\
  \Leftrightarrow a = \frac{{\left( {b + c} \right)\left( {3bc - b^2  - c^2 } \right)}}{{b^2  + c^2 }}\\
 \end{array}
\]
Kết hợp (*), ta có:\[
\left. \begin{array}{l}
 a > b \Leftrightarrow \frac{{\left( {c - b} \right)\left( {2b^2  - c^2 } \right)}}{{b^2  + c^2 }} > 0 \Leftrightarrow b > \frac{c}{{\sqrt 2 }} \\
 a < c \Leftrightarrow \frac{{\left( {c - b} \right)\left( {b^2  - 2c^2 } \right)}}{{b^2  + c^2 }} < 0 \Leftrightarrow b < c\sqrt 2  \\
 \end{array} \right\} \Rightarrow \frac{c}{{\sqrt 2 }} < b < c\sqrt 2 ,\left( {**} \right)
\]
BĐT cần chứng minh tương đương với

\[
\frac{1}{b} + \frac{1}{c} < \frac{{2\left( {b^2  + c^2 } \right)}}{{\left( {b + c} \right)\left( {3bc - b^2  - c^2 } \right)}} \Leftrightarrow \frac{{\left( {b - c} \right)^2 \left( {b^2  + 3bc + c^2 } \right)}}{{bc\left( {b + c} \right)\left( {b^2  - 3bc + c^2 } \right)}} < 0 \quad (3)
\]
Xét hàm $f(b)=b^2-3bc+c^2$ (cho $c$ cố định). Vì $f$ lõm và từ (**) nên

\[
f\left( b \right) = b^2  - 3bc + c^2  \le \max \left\{ {f\left( {c\sqrt 2 } \right);f\left( {\frac{c}{{\sqrt 2 }}} \right)} \right\} = \max \left\{ {\left( {3 - 3\sqrt 2 } \right)c^2 ;\left( {\frac{3}{2} - \frac{3}{{\sqrt 2 }}} \right)c^2 } \right\} < 0
\]
Như vậy (3) đúng. Ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-06-2013 - 08:25

[nguyenthehoan]

$\boxed{\text{Bài toán 37}}$ http://www.artofprob...opic.php?t=5889

Three circles $\kappa _{1},\kappa _{2},\kappa _{3}$ of radii $R_{1},R_{2},R_{3}$ respectively,pass through a point $O$ and intersect two by two in $A,B,C$,the point $O$ lies inside triangle $ABC$.Let $A_{1},B_{1},C_{1}$ be the intersections of $AO,BO,CO$ with the sides $BC,CA,AB$ of the triangle $ABC$.Denote $\alpha =\frac{OA_{1}}{AA_{1}},\beta =\frac{OB_{1}}{BB_{1}},\gamma =\frac{OC_{1}}{CC_{1}}$.Let $R$ be the radii of circumcircle of triangle $ABC$.Prove that:

$\alpha R_{1}+\beta R_{2}+\gamma R_{3}\geq R$.

 

============================================

 

Ba đường tròn $\kappa _{1},\kappa _{2},\kappa _{3}$ với bán kính lần lượt là $R_{1},R_{2},R_{3}$ cùng đi qua một điểm $O$ và đôi một cắt nhau tại một điểm thứ hai là $A,B,C$,điểm $O$ nằm trong tam giác $ABC$.Gọi $A_{1},B_{1},C_{1}$ là giao điểm của $AO,BO,CO$ với các cạnh $BC,CA,AB$.Kí hiệu $\alpha =\frac{OA_{1}}{AA_{1}},\beta =\frac{OB_{1}}{BB_{1}},\gamma =\frac{OC_{1}}{CC_{1}}$.Gọi $R$ là bán kính đường tròn ngoại tiếp tam giác $ABC$.Chứng minh rằng:

$\alpha R_{1}+\beta R_{2}+\gamma R_{3}\geq R$.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 07-06-2013 - 08:51

[perfectstrong]

$\boxed{\text{Bài toán 37}}$ http://www.artofprob...opic.php?t=5889

Three circles $\kappa _{1},\kappa _{2},\kappa _{3}$ of radii $R_{1},R_{2},R_{3}$ respectively,pass through a point $O$ and intersect two by two in $A,B,C$,the point $O$ lies inside triangle $ABC$.Let $A_{1},B_{1},C_{1}$ be the intersections of $AO,BO,CO$ with the sides $BC,CA,AB$ of the triangle $ABC$.Denote $\alpha =\frac{OA_{1}}{AA_{1}},\beta =\frac{OB_{1}}{BB_{1}},\gamma =\frac{OC_{1}}{CC_{1}}$.Let $R$ be the radii of circumcircle of triangle $ABC$.Prove that:

$\alpha R_{1}+\beta R_{2}+\gamma R_{3}\geq R$.

 

============================================

 

Ba đường tròn $\kappa _{1},\kappa _{2},\kappa _{3}$ với bán kính lần lượt là $R_{1},R_{2},R_{3}$ cùng đi qua một điểm $O$ và đôi một cắt nhau tại một điểm thứ hai là $A,B,C$,điểm $O$ nằm trong tam giác $ABC$.Gọi $A_{1},B_{1},C_{1}$ là giao điểm của $AO,BO,CO$ với các cạnh $BC,CA,AB$.Kí hiệu $\alpha =\frac{OA_{1}}{AA_{1}},\beta =\frac{OB_{1}}{BB_{1}},\gamma =\frac{OC_{1}}{CC_{1}}$.Gọi $R$ là bán kính đường tròn ngoại tiếp tam giác $ABC$.Chứng minh rằng:

$\alpha R_{1}+\beta R_{2}+\gamma R_{3}\geq R$.

Lời giải:

Ta sử dụng bổ đề trong bài 21:

Cho tam giác $ABC$ và $P$ là 1 điểm bất kì. Khi đó ta có:

\[
\sum {\frac{{PC.PB}}{{AB.AC}}}  \ge 1
\]
===========================

Quay lại bài toán.

Đặt $S_{ABC}=S$. Sử dụng định lý hàm sin trong $\triangle OBC$, ta có $R_1  = \frac{{BC}}{{2\sin BOC}}$.

Mặt khác:\[
\alpha  = \frac{{S_{BOA_1 } }}{{S_{BAA_1 } }} = \frac{{S_{COA_1 } }}{{S_{CAA_1 } }} = \frac{{S_{BOA_1 }  + S_{COA_1 } }}{{S_{BAA_1 }  + S_{CAA_1 } }} = \frac{{S_{BOC} }}{S}
\]

Kết hợp với nhau cho ta\[
\alpha R_1  = \frac{{S_{BOC} }}{S}.\frac{{BC}}{{2\sin BOC}} = \frac{{OB.OC.BC}}{{4S}}
\]
Lập các biểu thức tương tự rồi cộng lại, ta có:\[
\alpha R_1  + \beta R_2  + \gamma R_3  = \frac{{OB.OC.BC + OC.OA.AC + OA.OB.AB}}{{4S}}
\]
BĐT cần chứng minh trở thành:\[
\begin{array}{l}
 \frac{{OB.OC.BC + OC.OA.AC + OA.OB.AB}}{{4S}} \ge R \\
  \Leftrightarrow OB.OC.BC + OC.OA.AC + OA.OB.AB \ge 4SR = BC.CA.AB \\
 \end{array}
\]
Nhưng BĐT cuối lại đúng theo bổ đề nên ta có đpcm.

[barcavodich]

Bài toán $38$

Let $P$ be a point inside $\Delta ABC$.The perpendiculars from $P$ to $BC$,$CA$,$AB$ meet the circumcircle of $\Delta ABC$ in $X,Y,Z$ respectively . Show that the perpendiculars from $A$ to $YZ$,$B$ to $XZ$ and $C$ to $XY$ are concurrent

http://www.artofprob...=5189&view=next

 

 

Bài viết đã được chỉnh sửa nội dung bởi barcavodich: 07-06-2013 - 10:06

[nguyenthehoan]

Bài toán $38$

Let $P$ be a point inside $\Delta ABC$.The perpendiculars from $P$ to $BC$,$CA$,$AB$ meet the circumcircle of $\Delta ABC$ in $X,Y,Z$ respectively . Show that the perpendiculars from $A$ to $YZ$,$B$ to $XZ$ and $C$ to $XY$ are concurrent

http://www.artofprob...=5189&view=next

 

 

Đây chính là định lí Carnot về tam giác trực giao!Một định lí cơ bản của hình học phẳng.

[nguyenthehoan]

$\boxed{\text{Bài toán 39}}$ http://www.artofprob...opic.php?t=5588

Let $O$ be an interior point of an acute triangle $ABC$.The circle with centres the midpoints of its sides and passing through $O$ mutually intersect the second time at the points $K,L,M$ different from $O$.Prove that $O$ be the incentre of the triangle $KLM$ if and only if $O$ be the circumcentre of the triangle $ABC$

 

==============================================

 

Cho một điểm $O$ nằm bên trong tam giác nhọn $ABC$.Các đường tròn với tâm là trung điểm các cạnh tam giác và đi qua $O$ cắtnhau tại các điểm $K,L,M$ khác $O$.Chứng minh rằng $O$ là tâm nội tiếp tam giác $KLM$ khi và chỉ khi $O$ là tâm ngoại tiếp tam giác $ABC$.

 

P/s:Bài toán không khó và có một số mở rộng thú vị!!!

[The Collection]

$\boxed{\text{Bài toán 39}}$ http://www.artofprob...opic.php?t=5588

Let $O$ be an interior point of an acute triangle $ABC$.The circle with centres the midpoints of its sides and passing through $O$ mutually intersect the second time at the points $K,L,M$ different from $O$.Prove that $O$ be the incentre of the triangle $KLM$ if and only if $O$ be the circumcentre of the triangle $ABC$

 

==============================================

 

Cho một điểm $O$ nằm bên trong tam giác nhọn $ABC$.Các đường tròn với tâm là trung điểm các cạnh tam giác và đi qua $O$ cắtnhau tại các điểm $K,L,M$ khác $O$.Chứng minh rằng $O$ là tâm nội tiếp tam giác $KLM$ khi và chỉ khi $O$ là tâm ngoại tiếp tam giác $ABC$.

 

P/s:Bài toán không khó và có một số mở rộng thú vị!!!

 

Giải như sau:

 

 

Gọi $D,E,F$ lần lượt là trung điểm của các cạnh $BC,CA,AB$.

 

Ta có: $O,K$ là các giao điểm của $(D),(E)$ nên $OK \perp DE \to OK \perp BC$.

 

Và: $OF \perp BC$ do $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$.

 

Suy ra: $O,K,F$ thẳng hàng.

 

Tương tự: $L,O,D$ thẳng hàng và $M,O,E$ thẳng hàng.

 

Để ý $FD$ là trung trực của $OM$ nên $\angle FMD=\angle FOD$.

 

Tương tự: $\angle DKF=\angle DOK$.

 

Suy ra: $\angle FMD+\angle DKF=180^o$

 

Nên tứ giác $FMDK$ nội tiếp $\to \angle FMK=\angle FDK$.

 

Mặt khác tứ giác $FMDE$ nội tiếp do $\angle DFM=\angle DEO (=\angle DFO)$.

 

Nên tứ giác $FMKE$ nội tiếp $\to \angle MEO=\angle OFM \to \angle MLO=\angle KLO \to LO$ là phân giác của $\angle KLM$.

 

Tương tự thì $KO$ là phân giác của $\angle LKM$. Dĩ nhiên ta có đpcm.

 

___

 

 

Èo, post bài xong mới thấy cách chứng minh đơn giản hơn như sau:

 

 

Gọi $Q,R.S$ như hình vẽ, rõ ràng đó lần lượt là trung điểm của $OL,OM,OK$ và lần lượt là chân đường các đường cao của tam giác $FED$ nên $O$ là tâm đường tròn nội tiếp của tam giác $QRS$ (bổ đề quen thuộc). Để ý rằng $QR//LM, RS//MK, SQ//KL$ nên $O$ cũng là tâm đường tròn nội tiếp tam giác $MKL$, ta có đpcm. (ngắn hơn trên khá nhiều)

 

Bài viết đã được chỉnh sửa nội dung bởi tranminhbao2607: 07-06-2013 - 14:28

[perfectstrong]

Giải như sau:

 

hình.png

 

Gọi $D,E,F$ lần lượt là trung điểm của các cạnh $BC,CA,AB$.

 

Ta có: $O,K$ là các giao điểm của $(D),(E)$ nên $OK \perp DE \to OK \perp BC$.

 

Và: $OF \perp BC$ do $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$.

 

Suy ra: $O,K,F$ thẳng hàng.

 

Tương tự: $L,O,D$ thẳng hàng và $M,O,E$ thẳng hàng.

 

Để ý $FD$ là trung trực của $OM$ nên $\angle FMD=\angle FOD$.

 

Tương tự: $\angle DKF=\angle DOK$.

 

Suy ra: $\angle FMD+\angle DKF=180^o$

 

Nên tứ giác $FMDK$ nội tiếp $\to \angle FMK=\angle FDK$.

 

Mặt khác tứ giác $FMDE$ nội tiếp do $\angle DFM=\angle DEO (=\angle DFO)$.

 

Nên tứ giác $FMKE$ nội tiếp $\to \angle MEO=\angle OFM \to \angle MLO=\angle KLO \to LO$ là phân giác của $\angle KLM$.

 

Tương tự thì $KO$ là phân giác của $\angle LKM$. Dĩ nhiên ta có đpcm.

 

___

 

 

Èo, post bài xong mới thấy cách chứng minh đơn giản hơn như sau:

 

hinh 1.png

 

Gọi $Q,R.S$ như hình vẽ, rõ ràng đó lần lượt là trung điểm của $OL,OM,OK$ và lần lượt là chân đường các đường cao của tam giác $FED$ nên $O$ là tâm đường tròn nội tiếp của tam giác $QRS$ (bổ đề quen thuộc). Để ý rằng $QR//LM, RS//MK, SQ//KL$ nên $O$ cũng là tâm đường tròn nội tiếp tam giác $MKL$, ta có đpcm. (ngắn hơn trên khá nhiều)

tranminhbao2607 giải thiếu rồi. Đề yêu cầu 2 chiều mà đây mới có mỗi chiều đảo.

[The Collection]

tranminhbao2607 giải thiếu rồi. Đề yêu cầu 2 chiều mà đây mới có mỗi chiều đảo.

 

Dạ, em đọc thiếu đề ạ, chiều thuận giải quyết tương tự, ở đây đưa về giải quyết bài toán sau: Cho điểm $M$ nằm trong tam giác $ABC$ thoản mãn $M$ là tâm đường tròn nội tiếp tam giác $D,E,F$, ở đây $D,E,F$ lần lượt là chân đường vuông góc của $M$ tới $BC,CA,AB$. Khi đó $M$ là trực tâm của tam giác $ABC$.

 

Đây là bài toán quen thuộc, chứng minh như sau:

 

 

Ta có: $\angle FMA=\angle FEA = \angle DEC= \angle DMC (1)$

Mặt khác: $\angle FMD = 180^o - \angle FBD = 180^o - \angle FBM - \angle MBD$

Và $\angle MBD=\angle MFD= \angle MFE= \angle MAE$, tương tự $\angle FBM= \angle MCE$.

Suy ra: $\angle FMD=180^o-\angle MAE - \angle MCE = \angle AMC (2)$.

Từ $(1),(2)$ suy ra: $\angle FMC$ (chứa D)= $\angle FMC$ chứa $E$, mà $\angle FMC$ (chứa D)+ $\angle FMC$ chứa $E=360^o$, do đó có ngay $\angle FMC=180^o \to F,M,C$ thẳng hàng.

Tương tự, có $M$ là trực tâm của tam giác $ABC$.