Chủ đề này có 4 trả lời

[Doremon11]

Cho tứ diện ABCD có AB=BD=2a,Bc=a, tam giác BCD vuông tại C .Gọi E là trung điểm BD, biết (AB,CD)=60 

 a Tính 2AC²-AD² theo a 

 b (a) là mp song song AB,CE, cắt  BC,BD,AE,AC lần lượt tại M,N,P,Q .Tinh diện tích MNPQ theo a và x=BM( 0<x<a) .Định x để S ấy max

 c  Định x để tổng các bình phương của các đường chéo của MNPQ min

 dGọi O là giao điểm MP và NQ. Định (a) để OA²+OB²+OC²+OD² min

[perfectstrong]

Lời giải:

a) Chưa giải được.

b)

\[
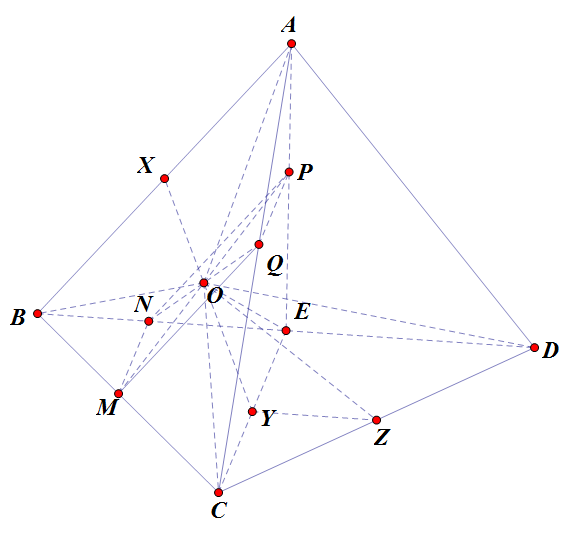
\begin{array}{l}
 \cos CBD = \frac{{BC}}{{BD}} = \frac{1}{2} \Rightarrow \angle CBD = 60^o  \Rightarrow \angle CDB = 30^o  \\
 CD = BC\tan 60^o  = a\sqrt 3  \\
 CE = BE = DE = \frac{1}{2}BD = a \\
 \end{array}
\]

$(a) \parallel CE \Rightarrow MN=(a) \cap (BCD) \parallel CE$.

Tương tự $PQ \parallel CE \Rightarrow MN \parallel MN$. Tương tự $NP \parallel MQ$. Suy ra $MNPQ$ là hình bình hành.

\[
\begin{array}{l}
 \frac{{MN}}{{CE}} = \frac{{BM}}{{BC}} \Rightarrow MN = x \\
 \frac{{MQ}}{{BA}} = \frac{{CM}}{{CB}} \Rightarrow MQ = 2\left( {a - x} \right) \\
 MN\parallel CE;MQ\parallel AB \Rightarrow \sin NMQ = \sin \angle \left( {CE;AB} \right):const \\
 S_{MNPQ}  = 2S_{MNQ}  = 2.\frac{1}{2}.MN.MQ.\sin NMQ = x.2\left( {a - x} \right)\sin \angle \left( {CE;AB} \right) \\
 \end{array}
\]

Từ đó, ta có:\[
S_{MNPQ}  \le \left( {x + a - x} \right)^2 \sin \angle \left( {CE;AB} \right) = a^2 \sin \angle \left( {CE;AB} \right)
\]
Đẳng thức xảy ra $\Leftrightarrow x=a-x \Leftrightarrow x=\dfrac{a}{2} \Leftrightarrow M$ là trung điểm $BC$.

c) \[
\begin{array}{l}
 MP^2  + NQ^2  = 4MO^2  + NQ^2  = 2\left( {MN^2  + MQ^2 } \right) - NQ^2  + NQ^2  = 2\left( {MN^2  + MQ^2 } \right) \\
  \Rightarrow MP^2  + NQ^2  = 2\left( {x^2  + 4\left( {a - x} \right)^2 } \right) = 10x^2  - 16ax + 8a^2  = 10\left( {x - \frac{4}{5}a} \right)^2  + \frac{8}{5}a^2  \ge \frac{8}{5}a^2  \\
 \end{array}
\]
Đẳng thức xảy ra $\Leftrightarrow x=\dfrac{4}{5}a$.

d) Gọi $X,Y,Z$ thứ tự là trung điểm $AB,CE,CD$.

\[
\begin{array}{l}
 \frac{{MB}}{{CB}} = \frac{{NB}}{{EB}} = \frac{{PA}}{{EA}} = \frac{x}{a} \Rightarrow \overrightarrow {OX}  = \frac{1}{2}\left( {\overrightarrow {OB}  + \overrightarrow {OA} } \right) = \frac{1}{2}\left( {\overrightarrow {OM}  + \overrightarrow {MB}  + \overrightarrow {OP}  + \overrightarrow {PA} } \right) \\
  = \frac{1}{2}\left( {\frac{x}{a}\overrightarrow {CB}  + \frac{x}{a}\overrightarrow {EA} } \right) = \frac{x}{a}.\frac{1}{2}\left( {\overrightarrow {CB}  + \overrightarrow {EA} } \right) = \frac{x}{a}\overrightarrow {YX}\\
 \end{array}
\]
Từ đó, suy ra $O$ chạy trên $YX$ và đồng thời: $\dfrac{OX}{YX}=\dfrac{x}{a}$ (*). Đặt $YX=t>0$ cố định.

\[
\begin{array}{l}
 OA^2  + OB^2  + OC^2  + OD^2  = 2OX^2  + \frac{{AB^2 }}{2} + 2OZ^2  + \frac{{CD^2 }}{2} = 2\left( {OX^2  + OZ^2 } \right) + \frac{7}{2}a^2  \\
 OZ^2  = OY^2  + YZ^2  - 2OY.YZ\cos OYZ = OY^2  - a\cos XYZ.OY + \frac{{a^2 }}{4} \\
  \Rightarrow OX^2  + OZ^2  = OX^2  + OY^2  - a\cos XYZ.OY + \frac{{a^2 }}{4} \\
  = \frac{{x^2 }}{{a^2 }}YX^2  + \frac{{\left( {a - x} \right)^2 }}{{a^2 }}YX^2  - a\cos XYZ.\frac{{a - x}}{a}YZ + \frac{{a^2 }}{4} \\
  = \frac{{2t^2 }}{{a^2 }}x^2  + \left( {\cos XYZ - \frac{{2t^2 }}{a}} \right)x + t^2  + \frac{{a^2 }}{4} - a\cos XYZ \\
 \end{array}
\]
Tới đây xét hàm theo $x$ trong $(0;a)$. Nhưng nó vẫn quá phức tạp. Chưa có cách nào hay hơn.

[Doremon11]

 phức tạp quá! 

Sau đây là 1 vài hint ,hi vọng sẽ giúp cho việc  tìm ra lời giải 

         câu a)  gọi  F là trung điểm Ad.Xét góc TH CEF =60 hoặc  =120 

         câu d) dùng tâm tỉ cự 

                OA² +OB²+OC²+OD² = 4OG²+GA²+GB²+GC² .MÀ O di động trên đoạn IJ ( đoạn nối trung điểm AB và CE nên chúng min khi O là hình chiếu  của G lên IJ hay G là trọng tâm (ABCD)

[chinhanh9]

Câu a: 

$(AB,CD)=60^{0}\Rightarrow (\overrightarrow {AB},\overrightarrow {CD})= 60^0\vee (\overrightarrow {AB},\overrightarrow {CD})= 120^0$

$\left | \overrightarrow{AB}.\overrightarrow{CD} \right |= 2a.a\sqrt {3}.\frac{1}{2}=a^2\sqrt3$

Đặt $AC=x$

$\overrightarrow{AB}.\overrightarrow{CD} = ( \overrightarrow{AC}+ \overrightarrow{CB}).\overrightarrow{CD}= \overrightarrow{AC}.\overrightarrow{CD}=-x.a\frac{\sqrt{3}}{2}$

$\Rightarrow x.a\frac{\sqrt{3}}{2}=a^{2}\sqrt{3}\Rightarrow x= 2a\Rightarrow 2AC^{2}-BD^{2}=4a^{2}$

Bài viết đã được chỉnh sửa nội dung bởi chinhanh9: 11-04-2013 - 16:44

[Ciel Kun]

Các bạn áp dụng và tính toán toàn sai thui!!!