babystudymaths

Do trong lời giải của mọi người đều đã chứng minh P là tâm của AIDL nên em ko chứng minh lại:

Đoạn còn lại là một hướng chứng minh khác cho đoạn sau của Nguyen Dinh Hoang

      geogebra-export.png   109.71K   64 Số lần tải

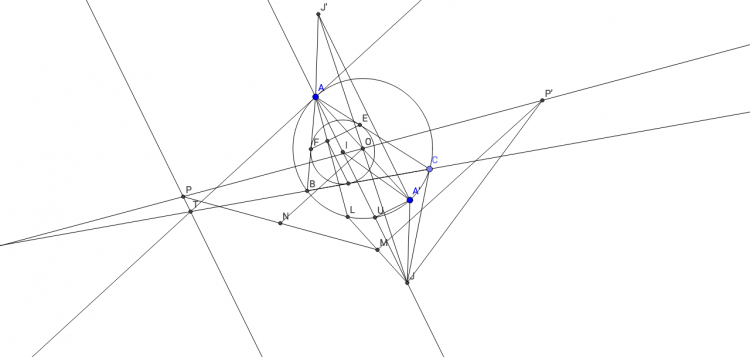
Gọi J' đối xứng với J qua O, A' đối xứng với A qua O => AJ'A'J là hình bình hành 

=>AJ' = A'J và A'J'// AJ => AI // A'J' (1) .

Gọi IJ cắt (O) tại U khác A thì U là trung điểm IJ, mà $A'U \perp IJ$ => A'I = A'J => AJ'= IA' (2)

Từ (1) và (2) => AIA'J' là hình thang cân. Mà P là trung trực AI => P là trung trực A'J'.

 Lấy P' đối xứng P qua O => P' là trung trực AJ, mà P' là trung trực AL=> P' là trung trực LM =>$P'M \perp LJ, mà P'M // ON => LJ \perp ON$

Lời giải của em ( chủ yếu là tính góc)
 Post 350.png   57.24K   59 Số lần tải
Ta có các kết quả sau đây là quen thuộc:
$AK$ vuông góc với $AP, AL$ vuông góc với $AQ, O$ là trung điểm $KL$, $\widehat{QAK} = \frac{\widehat{BAC}}{2} = \widehat{LAP}$
Xét phép vị tự tâm $A$ tỉ số 2 biến : $K\rightarrow G, L\rightarrow H$, $N\rightarrow B, M\rightarrow C, (AMN) \rightarrow (ABC)$ $\Rightarrow GE$ vuông góc $AC, HF$ vuông góc với $AB$.
$(K,KA) , (L, LA), (O)$ cắt nhau tại $A, T$.
Đặt $QF$ cắt $PE$ tại $T' \Rightarrow T'$ $\in$ $(O)$ ( $T'$ là điểm tiếp xúc của $(O)$ và đường tròn Mixtilinear $\bigtriangleup ABC$)
$\Rightarrow \frac{QT'}{PT'}=\frac{FT'}{ET'}=\frac{QF}{PE}\Rightarrow \frac{QK^{2}}{PL^{2}} = \frac{QA^{2}}{PA^{2}}= \frac{QB^{2}}{PC^{2}} = \frac{QF. QT'}{PE. PT'} = \frac{QT'^{2}}{PT'^{2}}\Rightarrow \bigtriangleup QKT' \sim \bigtriangleup PLT'$
$\Rightarrow \widehat{KT'L} = \widehat{QT'L} = \widehat{QTP} = \widehat{KTL} \Rightarrow $ $T'$ $\in$ $(O)$ ,dễ chứng minh $\bigtriangleup QKT \sim \bigtriangleup PLT, T \in (O)$ $\Rightarrow T'\equiv T$.
Đường thẳng bất kỳ qua $A$ cắt $(O)$ tại $X$, cắt $(K, KA)$ tại $Y$, cắt $(L, LA)$ tại $Z$.
Đặt $EY$ cắt $FZ$ tại $D$.
Ta có $180^\circ - \widehat{FDE} = \widehat{FED} + \widehat{EFD} = \widehat{FEG} + \widehat{GAY} + \widehat{HAZ} + \widehat{EFR} = \widehat{BAC} + \widehat{KAL} = \widehat{QAP} = \widehat{ETF}$
$ \Rightarrow D \in (FTE)$
Ta cũng có $\widehat{PTD} = \widehat{EFD} = \widehat{HFZ} + \widehat{EFR} = \widehat{LAY} + \frac{\widehat{BAC}}{2} = \widehat{PAX} = \widehat{PTX}$
$\Rightarrow T, D, X$ thăng hàng. ($R$ là tâm đường tròn Mixtilinear của tam giác ABC ).
Mặt khác $\widehat{XYT} = \widehat{CET} = \widehat{EFT} = \widehat{XDY} \Rightarrow XY^{2} = XD. XT$.
Dễ chứng minh $X$ là trung điểm $YZ , (X, YZ:2 )$ cắt $(O)$ tại $U',V' \Rightarrow XU'^{2}= XV'^{2}= XY^{2}$, dễ dàng suy ra $U'V'$ tiếp xúc $(FTE)$ tại $D$.
Mà $(YZ)$ là ảnh của $(UV)$ qua phép vị tự tâm $A\Rightarrow U'V'$ là ảnh của trục đẳng phương của $(UV)$ và $(AMN)$
$\Rightarrow $ trục đẳng phương của $(UV)$ và $(AMN)$ luôn tiếp xuc với 1 đường tròn cố định.

      Từ ngày 24/8 đến ngày 31/8 , Trường THPT chuyên Hùng Vương Phú Thọ đã tổ chức Trường Thu Toán học Hùng Vương vs sự tham gia của hơn 60 học sinh đến từ các tỉnh trung du và miền núi phía Bắc. Đội ngũ giảng dạy là các thầy giáo trong trường có nhiều kinh nghiệm trong việc bồi dưỡng học sinh giỏi Toán Olympic và các cựu học sinh trong trường đã từng đạt giải Quốc tế và dự thi vòng TST. 

      Kết thúc Trường Thu đã có một bài kiểm tra để đánh giá kết quả mà các học sinh đã nhận được sau kỳ học. Mình đăng lên đây để mọi người cùng thảo luận.

                                                               20160830_103001.jpg   32.84K   58 Số lần tải

Cho tam giác $ABC$ nội tiếp đường tròn $(O). P$ là điểm bất kì trong tam giác. $AP, BP, CP$ lần lượt cắt $BC, CA, AB$ tại $A_{1}, B_{1}, C_{1}$. $(AB_{1}C_{1}) , (BA_{1}C_{1}), (CB_{1}A_{1})$ lần lượt cắt $(O)$ tại điểm thứ 2 là $A_{2}, B_{2}, C_{2}$.

$Q$ là điểm bất kì trong tam giác . $AQ, BQ, CQ$ lần lượt cắt $BC, CA, AB$ tại $A_{3}, B_{3}, C_{3}$. $A_{2}A_{3}, B_{2}B_{3},C_{2}C_{3}$ lần lượt cắt $(O)$ tại điểm thứ 2 là $A_{4}, B_{4}, C_{4}$. 

Chứng minh rằng $AA_{4}, BB_{4}, CC_{4}$ đồng quy.

Em xin đóng góp một lời giải khác

 mayqua.png   119.77K   37 Số lần tải

$AP$ cắt $EF$ tại $T$. 

Đặt $(FTP)$ cắt $AB$ tại $H. ( TEP)$ cắt $AC$ tại $K$.

Ta có : $AF. AH = AT. AP = AK. AE \Rightarrow F, K, E, H$ đồng viên. $\Rightarrow \widehat{AHK} = \widehat{AEF} = \widehat{APK}$ 

$\Rightarrow A, H, P, K$ đồng viên  

$\Rightarrow \widehat{HKP} = \widehat{HAP} = \widehat{BCP}, \widehat{KHP} = \widehat{KAC} = \widehat{CBP}$

$\Rightarrow \triangle BPC \sim \triangle HPK$. Đặt $HK$ cắt $BC$ tại $M'$ thì  $M', K, C, P$ đồng viên.

Mặt khác $\triangle BPC \sim \triangle PFA \Rightarrow \triangle AFT \sim \triangle CPM$

$\Rightarrow \widehat{CPM} = \widehat{AFT} = \widehat{APH} = \widehat{AKM'} = \widehat{CPM'}$

$\Rightarrow M \equiv M' \Rightarrow \widehat{AKM} = \widehat{AFE} = \widehat{ANE}$

$\Rightarrow AM. AN = AK. AE = AT. AP \Rightarrow 2AM. AN = AP^{2}$

Kết thúc chứng minh. 

Tìm tất cả các bộ số nguyên dương (x, y, z) thoả mãn

$3^{x}- 2^{y}= 19^{z}$

Mọi người giải nhanh quá. Em xin đóng góp thêm một lời giải khác cho bài toán gốc.

 geogebra-export (3).png   57.24K   147 Số lần tải

Qua $O$ kẻ đường thẳng song song $AD$, cắt $BM, CN$  lần lượt tại $E, F$.

Từ đó suy ra $EB=EM=EA, FC=FN=FD \Rightarrow SE\perp AB, TF\perp AB\Rightarrow SE\parallel AB, TF\parallel CD$

Lấy $L$ đối xứng $P$ qua $EF$ thì $L\in (O)$ . Do tính đối xứng nên $\overline{A, E, L}  và  \overline{D, F, L}$ .

Lấy $J$ là trung điểm $ST\Rightarrow JS=JT=JO$.

Mặt khác $\widehat{ESO}=\widehat{EOS}=45^\circ, \widehat{FTO}=\widehat{FOT}=45^\circ\Rightarrow ES=EO, FT=FO$

$\Rightarrow JE\perp SO, JF\perp TO\Rightarrow JE\perp JF.$. Mà$\widehat{JEF}=\widehat{JFE}=45^\circ$

$\Rightarrow JE=JF$.

Mặt khác $\widehat{ELF}= 45^\circ=\frac{1}{2} \widehat{EJF}\Rightarrow JL= JE= JF\Rightarrow L, J, O$  thẳng hàng ( vị tự ).

Mà $\widehat{UEL}=2 \widehat{BAL}=\widehat{BOL}= \frac{1}{2} \widehat{UJL}\Rightarrow U\in (J,JE)\Rightarrow JU= JL$

Tương tự $JL=JV\Rightarrow L\in (UV)$ 

Rõ ràng, ta suy ra $(UV)$ tiếp xúc $(O).\blacksquare$

Tìm các số nguyên dương k,m,n thoả mãn 

$k^{m}\mid m^{n}-1 ; k^{n}\mid n^{m}-1$

Em có cách khác. (Em mất cả trưa vẫn chưa tìm được cách up cái hình lên, mong mọi người thông cảm)

Ta có : $\angle FDM=\angle ABM=\angle ACN= \angle EDN\Longrightarrow \angle FDA=\angle EDA.$ Mà $\angle FAD=\angle EAD\Longrightarrow AF=AE, DF=DE. \angle EDF=\angle FDM +\angle EDN = \angle ABM + \angle ACN= 180^\circ- 2\angle BAC. \Longrightarrow \angle DFE=\angle DEF=\angle FAE \Longrightarrow DF, DE$  là  tiếp  tuyến của $D$ với $\odot (AEF)$

$BE$ cắt $\odot (AEF)$ tại $I$ khác $E,FI$ cắt $AE$ tại $C'$

Áp dụng định lý $Pascal$ cho $6$ điểm $\begin{pmatrix} F & A & E\\ E & I & F \end{pmatrix}$

$\Longrightarrow B, D, C'$ thẳng hàng $\Longrightarrow C'\equiv C$

$BC$ cắt $QP$ tại $S,AI$ cắt $BC$ tại $G$.

-Xét $\odot (AEF)\Longrightarrow B,C$ liên hợp với $G\Longrightarrow S$ liên hợp với $G$. 

Mà $SA$ tiếp xúc $\odot (AEF)$ tại $A\Longrightarrow SI$ tiếp xúc với $\odot (AEF)$ tại $I\Longrightarrow S$ thuộc trung trực $AI$.

Goi $EP,FQ$ lần lượt cắt $\odot (AEF)$ tại $X,Y\Longrightarrow X,Y$ thuộc trung trực $AI\Longrightarrow  S,X,Y$ thẳng hàng.

Mặt khác , dễ thấy $PXYQ$ nội tiếp $\Longrightarrow SA^{2}= SX. SY= SP. SQ$

Lấy $Z$ đối xứng của $A$ qua $S$ thì $(Z,A, P, Q) = -1\Longrightarrow ( S, A, K, L) = -1\Longrightarrow H (S, A, K, L) =-1$

Mà $\angle SHA = 90^\circ\Longrightarrow HA$ là phân giác $\angle KHL.\blacksquare$

Câu hình lúc đi thi bị rối nên làm hơi ẩu

Áp dụng định lý Pascal cho 6 điểm (F, E, D

                                                          P, D, E )

Ta có M, L, c thăngr hàng.

 Kéo dài È cắt BC tại T, MD cắt BF tại X . 

Ta có (T, D, B, C) = -1 thì T, X, L thẳng hàng

Áp dụng định lý Desargues Cho tam giác MPE và BFD có giao điểm của các đoạn thẳng tương ứng thẳng hàng=> MB, PF, DE đồng quy.

Mà theo định lý Brocard thì IL vuông góc với BM, mà LK cx vuông góc  với BM.

Vậy I, L, K thẳng hàng

( đi thi quên ko cm M, L, C thẳng hàng vì nó hiển nhiên quá, ko biết có việc gì Ko)

( em đăng vội nên ko up được hình, mong mọi người thông cảm)

Em nghĩ bài toán gốc có thể dựng thêm các điểm liên hợp đẳng giác trong các tam giác $BDC,ABE,ACF$, nhưng chưa chứng minh được tiếp.

Như vậy đã có lời giải bài toán cũ trong tuần 3 tháng 4 và kèm theo là bài toán mới:

 

Bài 35: Cho tam giác $ABC$ nhọn trực tâm $H$, nội tiếp đường tròn $(O). HB,HC$ lần lượt cắt một tiếp tuyến thay đổi của $(O)$ tại $E,F.K$ đối xứng với $H$ qua $EF$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KEF$ luôn tiếp xúc một đường tròn cố định khi tiếp tuyến thay đổi.

Post 62.png

Hình vẽ bài toán

Em không có phần mềm hỗ trợ vẽ hình, mong thầy và các bạn thông cảm

 - Lời giải

Gọi $J$ là điểm tiếp xúc của tiếp tuyến $EF$ với $(O)$

$CH, BH$ lần lượt cắt đường tròn $(O)$ tại điểm thứ 2 là $Q,P \Rightarrow Q,P$ thuộc đường tròn $(A, AH)$

$JQ, JP$ lần lượt cắt $(A,AH)$ tại điểm thứ 2 là $M,N$. Ta có

$\angle PMQ =\frac{1}{2}\angle PAQ =\frac{1}{2} (180^{0}-\angle PJQ) \Rightarrow \angle PMJ =\angle MPJ \Rightarrow JM=JP, JN=JQ \Rightarrow MN=PQ$

$EM$ cắt $(A, AH)$ tại điểm thứ 2 là $I, IN$ cắt $QH$ tại $F'.$

Áp dụng định lý $Pascal$ cho 6 điểm 

$(I, P, Q$

$H, M, N) \Rightarrow E, J, F'$ thẳng hàng$\Rightarrow F' \equiv F$

Ta có

$\angle EIF=\angle MIN =\angle QIP =\frac{1}{2}\angle QAP =\angle BAC =180^{0}-\angle BHC= 180^{0}- \angle EKF$

$\Rightarrow I$ thuộc $(EKF)$

Mà $\angle MJE = \angle QPJ= \angle JMN$

$\Rightarrow MN // EF \Rightarrow (EKF)$ tiếp xúc $(A, AH)$ tại $I.\blacksquare$

Cho a, b, c là 3 số thục dương. CMR

$\sum \frac{a^{4}}{b\sqrt{5c^{6}+4(ab)^{3}}}\geq 1$

$4(a+b+c)-3abc\geq 3(ab+bc+ca)$

 

$a + b + c + abc \ge 4\sqrt[4]{a^2b^2c^2} = 4\sqrt{abc} => 1 \ge abc => a + b + c \ge 3 => a + b + c \ge 3abc$

Mà $a, b, c \ge 0 => a + b + c \leq 4$

$=> (a + b + c -3)(a + b + c -4) \leq 0$

$<=> (a + b + c)^2 - 7(a + b +c) + 12 \leq 0$

$<=> 4(a + b + c) - 3abc \ge (a + b + c)^2 \ge 3(ab + bc + ca)$

$=> a + b + c \ge ab +bc + ca (Do$  $a + b + c \ge 3abc) (đ.p.c.m)$

Bài toán trên có hai dấu "=" là (1,1,1) và (0,2,2) 

Theo bài làm của bạn thì $(a+b+c)^{2}\geq 3(ab+bc+ca)$ và $a+b+c\geq 3abc$

Tại (0,2,2) thì dấu "=" không xảy ra

Hơn nữa, do  $a+b+c\geq 3abc$ và $4(a+b+c)-3abc\geq 3(ab+bc+ca)$ không thể suy ra được điều phải chứng minh hay sao ấy

Cho mình xin câu 1

Vì a, b, c thuộc đoạn [-1; 1] => $1\geq a^{2}, 1\geq b^{2}, 1\geq c^{2} => \prod (1-a^{2})\geq 0 <=> 1+\sum a^{2}b^{2}- [(abc)^{2}+\sum a^{2}]\geq 0$ (1)

Từ gt ta có 

$2abc\geq a^{2}+b^{2}+c^{2}-1 =>4(abc)^{2}\geq \sum a^{4}+2\sum a^{2}b^{2} -2\sum a^{2} +1 <=> 1+2(abc)^{2}-\sum a^{4}\geq 2(\sum a^{2}b^{2}+1-\sum a^{2}-(abc)^{2})\geq 0$ (suy ra từ (1))

=>$1+2(abc)^{2}\geq \sum a^{4}$