Minhnksc

Bài 99:(Sưu tầm)

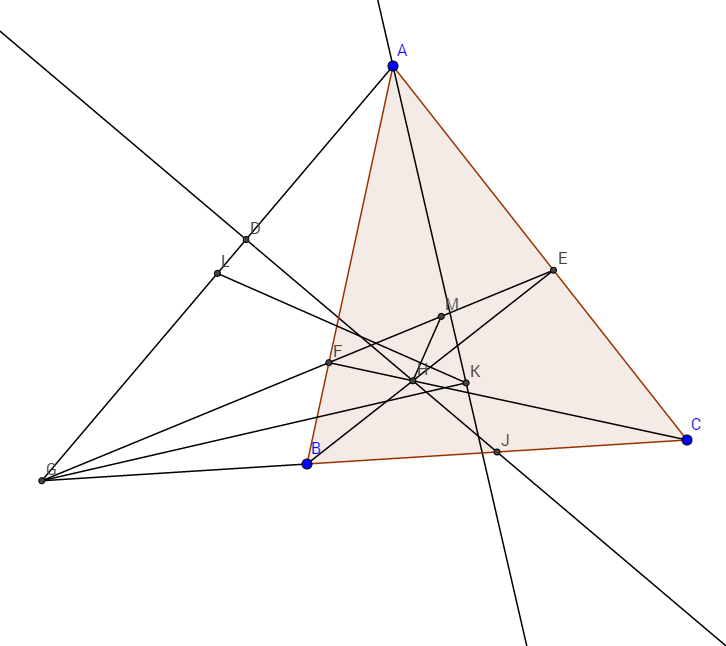
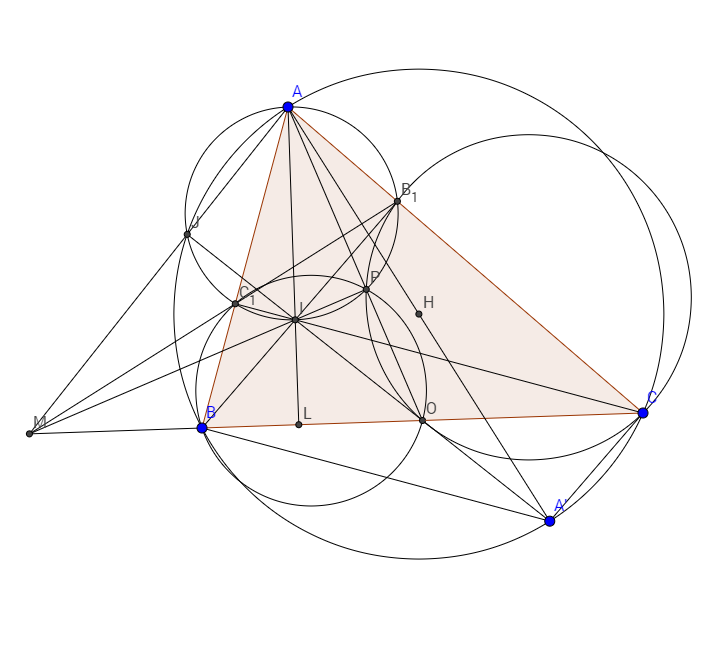
Cho hình bình hành $ABCD$; phân giác góc $BCD$ cắt $AB$ và $AD$ lần lượt ở $I$ và $J$. Đường tròn $(AIJ)$ và $(ABD)$ cắt nhau ở $M$. Chứng minh $M$ luôn thuộc một đường tròn cố định khi $A;C$ cố định còn $B;D$ thay đổi.

P/S:Ai sẽ là người vinh dự được đăng bài toán $100$ đây ???

Bài 97 : (Nguyễn Duy Khương chuyên Hà Nội AMS)

Cho tam giác $ABC$ có đường cao $BE,CF$ cắt nhau tại $ H$. $EF$ cắt $BC$ tại $G$. $K$ là hình chiếu của $G$ lên phân giác trong góc $BAC$. $L$ là trung điểm $AG$. Chứng minh rằng: đường thẳng qua $H$ vuông $KL$ chia đôi $EF$.

P/s: Hóng lời giải bài của anh Khương lắm ạ.

Bổ đề: Cho tam giác $ABC$ có trực tâm $H$;đường cao $BE$; $CF$;$G$ là giao điểm của $EF$ và $BC$; $J$ là trung điểm của $BC$. Chứng minh $JH\perp AG$

(Bổ đề này là một phần của bài toán $83$; mình không chứng minh lại)

Trở lại bài toán:

Gọi giao điểm của $JH$ và $AG$ là $D$

Từ bổ đề; ta suy ra $\widehat{ADH}=90^0=\widehat{AFH}$ nên $ADFH$ nội tiếp$\Rightarrow \widehat{DAF}=\widehat{DHF}=\widehat{JHC}$

Gọi $M$ là trung điểm của $DE\Rightarrow \Delta JHC \sim \Delta MHE\Rightarrow \widehat{MHE}=\widehat{JHC}=\widehat{DAF}$

Do đó $\widehat{MHD}=\widehat{DHE}-\widehat{DMF}-\widehat{MHE}=180^0-\widehat{BAC}-2\widehat{DAF}$

Ta lại có tam giác $ALK$ cân tại $L$ và $\widehat{GAL}=\widehat{DAF}+\frac{\widehat{BAC}}{2}$

nên $\widehat{ALK}=180^0-\widehat{BAC}-2\widehat{DAF}=\widehat{MHD}(1)$

Đặt $\alpha=\widehat{MHD}$

Từ $(1)$ ta quay đường thẳng $AG$ và $JH$ lần lượt quanh điểm $L$ và $H$ một góc $\alpha$ thì thu được hai đường thẳng mới là $KL$ và $MH$

Do đó vì $JH\perp AG$ nên $KL\perp MH$ (đpcm)

Câu cuối:

Nếu đầu tiên ta đặt một điểm vào trong một tứ giác thì ta được 4 tam giác. Sau đó đặt tiếp điểm thứ 2 vào tứ giác thì điểm thứ 2 này nằm trong một trong 4 tam giác trên; nối điểm này tới các đỉnh của tam giác chứa nó ta thấy rằng tổng số tam giác lúc này tăng thêm 2; cứ như vậy 2011 lần nữa ta có tổng cộng 4028 tam giác không có điểm trong chung và tổng diện tích các tam giác này bằng $1 cm^2$. Do đó tồn tại một tam giác trong số các tam giác trên có diện tích nhỏ hơn $\frac{1}{4028} cm^2$

Còn câu nữa xử nốt cho nó lành

Câu II 

2)Gọi $X_{n}$ là số cách sắp xếp n người ($n\geq 0$) thỏa mãn đề bài (coi như $X_{0}=1$ vì khi không có người nào đứng thì chỉ có một cách sắp xếp duy nhất )

Giả sử chiều cao của $n$ người trên lần lượt là $a_{1};a_{2};...;a_{n}$ sao cho với $i>j$ thì $a_{i}>a_{j}$

Khi đó; giả sử người có chiều cao là $a_{1}$ đứng ở vị trí thứ $k$($0\leq k\leq n$) thì mỗi người đứng ở vị trí từ $1\rightarrow k$ luôn cao hơn tất cả những người đứng trước vì nếu ngược lại thì tồn tại một người có chiều cao nhỏ hơn $a_{1}$ (vô lý) $\Rightarrow$ người đứng ở vị trí thứ 1 là người cao nhất và có chiều cao $a_{n}$

Tương tự; người đứng ở vị trí thứ 2 có chiều cao là $a_{n-1}$

                 người đứng ở vị trí thứ 3 có chiều cao là $a_{n-2}$

                 .............

                 người đứng ở vị trí thứ $k-1$ có chiều cao là $a_{n-k}$

Do đó với mọi $0\leq k\leq n$ thì chỉ có một cách sắp sếp những người đứng ở vị trí từ 1 đến k sao cho thỏa mãn đề bài. Từ đó suy ra số cách sắp xếp n người thỏa mãn đề bài khi người thấp nhất (có chiều cao $a_{1}$) đứng ở vị trí thứ $k$ chính bằng số cách sắp xếp $n-k$ người đứng từ vị trí thứ $k+1$ trở đi ($=X_{n-k}$).

Vì vậy; khi cho $k$ lần lượt bằng $n;n-1;...;1$ thì ta nhận được số cách sắp xếp $n$ người lần lượt là $X_{0};X_{1};X_{2};...;X_{n-1}$

Mà tổng số cách sắp xếp $n$ người bằng tổng các số trên nên $X_{n}=X_{0}+X_{1}+...+X_{n-1}$

Lại có $X_{0}=1$ và $X_{1}=1$ nên từ công thức trên và bằng phương pháp quy nạp ta chứng minh được $X_{n}=2^{n-1} (n\geq 1)$

Thay $n= 10$ vào trên ta có $X_{10}=512$

P/S: Mới off có sáng với chiều chủ nhật để đi chơi mà tối lên diễn đàn đã thấy đề KHTN bị "xơi" gần hết rồi; còn mỗi cấu tổ

Một vài bài về cực hạn nào

$\boxed{3}$ Cho tập hợp $M$ là các điểm trên một mặt phẳng; trong đó mỗi trung điểm của hai đoạn thẳng nối hai điểm bất kì thuộc $M$ là một điểm thuộc $M$. Chứng minh $M$ là một tập hợp vô hạn

(Đọc kỹ đề bài nhé; chứ không lại bảo mình đăng trùng bài với ví dụ )

$\boxed{4}$ Cho $n$ điểm phân biệt trên một mặt phẳng; trong đó mỗi đường thẳng bất kì đi qua 2 điểm trong $n$ điểm trên đều đi qua một điểm thứ 3. Chứng minh rằng $n$ điểm đã cho thẳng hàng.

Lâu lắm rồi mình chưa thấy người lập ra topic này - Bạn Hoangkhanh2002 và các mem qua topic. Vì vậy, hôm nay mình sẽ quyết định viết tiếp chuyên đề mới; mình nghĩ chuyên đề PT-BĐT kết thúc ở đây được rồi do PT thì các bài tập trên topic + kiến thức HSG là đủ thi chuyên, còn BĐT thì đang được thảo tiếp tục thảo luận tại topic của bạn Tăng trong box BĐT - Cực trị. Mong các bạn hưởng ứng

$\boxed{\text{Chuyên đề}}$ Tổ hợp - Toán rời rạc

I)Một số phương pháp giải cơ bản

1, Nguyên lý Dirichlet: Giả sử dùng n hộp để cất r vật thì tồn tại 1 hộp chứa ít nhất $[\frac{r}{n}]$ vật

Ví dụ : Chứng minh tồn tại $k\in \mathbb{N}$ sao cho $1983^k-1\vdots 10^5$

Cho k lần lượt $10^5+1$ giá trị liên tiếp từ 1 trở đi ta được $10^5+1$ giá trị khác nhau của $1983^k-1$. Theo nguyên lý Dirichlet thì tồn tại hai số trong các số trên có cùng số dư khi chia cho $10^5$; giả sử là $1983^i-1$ và $1983^j-1$ (i>j)

$\Rightarrow (1983^i-1)-(1983^j-1)\equiv 0(mod 10^5)\Rightarrow 1983^j(1983^{i-j}-1)\equiv 0(mod 10^5)$

mà $gcd(1983,10)=1$ nên ta có $1983^{i-j}\equiv 0(mod 10^5)$(đpcm)

2,Nguyên tắc cực hạn: Trong một tập hợp hữu hạn các phần tử; luôn tồn tại một phần tử có giá trị lớn nhất; một phần tử có giá trị nhỏ nhất

Ví dụ: Trên một đường thẳng cho 1 tập hợp điểm M sao cho mỗi trung điểm của đoạn nối hai điểm thuộc M là một điểm thuộc M. Chứng minh tập hợp M là một tập hợp vô hạn

Giả sử đường thẳng đã cho được đặt nằm ngang và  tập hợp M hữu hạn

Khi đó trong M tồn tại một điểm nằm tận cùng bên trái. Giả sử là A, rõ ràng vì A nằm tận cùng bên trái nên A không thể là trung điểm của bất cứ đoạn nào nối hai điểm thuộc M (vô lý). Vậy tập hợp M vô hạn

3,Đại lượng bất biến : có thể hiểu là một đại lượng không đổi sau một hoặc một số thao tác

Ví dụ: Trên một cái bảng ghi các số : 1;2;3;...;2002. Ta thực hiện các thao tác sau: xóa hai số bất kì trên bảng và thay bằng tổng hoặc hiệu của chúng. Hỏi số còn lại cuối cùng trên bảng có thể là số 0 hay không?

Ta thấy rằng khi thay hai số a và b bằng $a-b$ (hoặc $a+b$) thì tổng các số trên bảng giảm (hoặc tăng) 2b là một số chẵn. Do đó tính chẵn lẻ 

của tổng các số trên bảng luôn không đổi tính chẵn lẻ (Đây chính là bất biến)

mà $1+2+3+...+2002$ là một số lẻ nên số cuối cùng trên bảng phải là số lẻ. Vậy số cuối cùng trên bảng không thể là số 0

Mình khởi đầu bằng hai bài

$\boxed{1}$ Chứng minh rằng trong 5 số mà trong mỗi số chỉ có ước nguyên tố là 3 và 5 tồn tại hai số mà tích của chúng là số chính phương

$\boxed{2}$ Cho một hình chữ nhật 5 x m gồm các ô vuông 1 x 1. Cho biết rằng có thể đặt các quân domino kích thước 1 x 2 vào hình chữ nhật sao cho quân domino phủ kín hình chữ nhật và trong hai ô 1 x 1 của quân domino; có một ô chứa dấu $(+)$ và một ô chứa dấu $(-)$; tích của  dấu trong các ô trong cùng một hàng và trong cùng một cột đều dương.

Chôm chỉa câu tổ phát nào

Bài 5

Gọi tập hợp $55$ số được chọn là $A=\begin{Bmatrix} a_{1};a_{2};...;a_{55} \end{Bmatrix}$ và tập hợp $B=\begin{Bmatrix} b_{1};b_{2};...;b_{55} \end{Bmatrix}$ sao cho $b_{i}=a_{i}+9$ với $i=\overline{1,55}$

Trong tập B có nhiều nhất 9 số lớn hơn 100$\Rightarrow$ tập B có ít nhất $55-9=46$ số không nhỏ hơn 100 và gọi $C$ là tập các số trên

Tổng các phần tử của hai tập $C$ và $A$ không nhỏ hơn $46+55=101$

Mà các phần tử ở hai tập hợp đều nhận nhiều nhất 100 giá trị và giá trị các phần tử ở hai tập $B$ và $C$ là phân biệt nên tồn tại một phần tử ở tập $B$ và một phần tử ở tập $C$ có giá trị bằng nhau; gọi là $a_{j}$

Vì $a_{j}\in C$ nên tồn tại $a_{k}\in A$ thỏa $a_{j}=a_{k}+9$

mà $a_{j}\in A$ nên trong 55 số được chọn thì tồn tại 2 số có hiệu bằng 9.

Liệu MU có vô địch C2 ??? Mà thôi; có vẻ C2 giờ nhiễm chì nên chả ai xem thì phải

Ừ, Minhnksc cũng ở Phủ Lý à? Năm nay có định thi chuyên không?

Mình không ở Phủ Lý nhưng mãi mới tìm thấy người Hà Nam trên diễn đàn.

"Ra lò" thêm bài nữa nào:

Bài 92:(thi thử chuyên KHTN đợt V 2012-2013)

Cho tam giác $ABC$; tiếp tuyến tại $B$ và $C$ cắt tiếp tuyến tại $A$ của đường tròn ngoại tiếp tam giác $ABC$ lần lượt ở $D$ và $E$. $CD$ cắt $AB$ ở $P$; $BE$ cắt $AC$ ở $Q$. Gọi $M$ và $N$ lần lượt là trung điểm của $CP$ và $BQ$. Chứng minh$\widehat{CBM}=\widehat{BCN}$

P/s:Nhanh thật; sắp 100 bài rồi đấy; không biết cái dự án tổng hợp các bài toán trên topic này của bác Tăng thế nào rồi nhỉ?

                                                                                            " Góp vui cho topic "   

Mình xin tham gia topic và mở đầu bằng hai bài toán .

Bài 89 ( APMO 2000 ): Cho tam giác ABC với trung tuyến AM và phân giác AN . Đường thẳng vuông góc với AN tại N cắt AB và AM lần lượt tại P và Q . Đường thẳng vuông góc với AB tại P cắt AN tại O . Chứng minh rằng OQ vuông góc với BC . 

Bài 90 ( sưu tầm ) : Cho tam giác ABC có I là trung điểm BC , đường thẳng d đi qua I cắt AB , AC lần lượt tại M và N , đường thẳng d' đi qua I cắt AB ,AC lần lượt tại Q và P ( M và P nàm cùng phía với BC ) . MP , NQ cắt BC tại E và F . Chứng minh rằng IE = IF .

Lời giải bài 89:

Ta có bổ đề sau:

Bổ đề: Cho tam giác $ABC$; trung điểm $K$ của $BC$; $M\in AB; N\in AC; I$ là trung điểm của $MN$ sao cho $\overline{A;I;K}$. Chứng minh $MN\parallel BC$

Qua $K$ kẻ $M'N'$ song song với $BC$ ($M'\in AB;N'\in AC$). Theo hệ quả định lý $Thalès$; ta dễ dàng suy ra $K$ là trung điểm của $MN$

+) Nếu $M'\neq M; N'\neq N \Rightarrow MM'N'M$ là hình bình hành $\Rightarrow MM'\parallel NN'$(vô lý)

Do đó $M'\equiv M; N'\equiv N\Rightarrow MN\parallel BC$ 

Trở lai bài toán:

Gọi giao điểm của $PQ$ và $AC$ là $E$
Dễ dàng chứng minh $OE\perp AC$ và tam giác $OPE$ cân ở $O\Rightarrow \hat{OPQ}=\hat{OEQ}(1)$
Qua $Q$ kẻ đường thẳng vuông góc với $OQ$ cắt $AC$ và $AB$ lần lượt ở $F$ và $D$
Từ đó ta có $OQDP$ và $OQEF$ là các tứ giác nội tiếp$\Rightarrow \hat{ODQ}=\hat{OPQ}$ và $\hat{OFQ}=\hat{OEQ}$
Kết hợp với $(1)$ ta có $\hat{ODQ}=\hat{OFQ}\Rightarrow$ tam giác $OFQ$ cân ở $O$
mà $OQ\perp FD\Rightarrow Q$ là trung điểm của $FD$

Áp dụng bổ đề; ta suy ra $FD\parallel BC$

Mà $OQ\perp FD\Rightarrow$ đpcm

Mình xin đề xuất bài toán tiếp theo (bài này ảo)

Bài 87(EGMO 2017):

Cho tam giác $ABC$ với tâm đường tròn ngoại tiếp $O$ và trọng tâm $G$. Gọi $O_{1};O_{2};O_{3}$ là điểm đối xứng của $O$ lần lượt qua $BC;AC;AB$; $G_{1};G_{2};G_{3}$ là điểm đối xứng của $G$ qua $BC;CA;AB$. Chứng minh rằng đường tròn ngoại tiếp các tam giác $O_{1}O_{2}C; O_{2}O_{3}A; O_{3}O_{1}B; G_{1}G_{2}C; G_{2}G_{3}A; G_{1}G_{3}B$ và $ABC$ có một điểm chung.

P/s: bạn Uchiha sisui sửa bài 84 thành 86 nhé.

Lời giải khác cho bài 83:

Bổ đề :Cho tam giác $ABC$ có đường cao $CC_{1}$; $BB_{1}$; $O$ là trung điểm của $BC$. Chứng minh $(BC_{1}O)$ và $(CB_{1}O)$ cắt nhau trên $AO$

(giống của bạn Mr.Cooper; mình xin không nhắc lại)

Trở lại bài toán 

Áp dụng bổ đề ta có $\overline{A;P;O}$

Gọi $I$ là giao điểm của $BB_{1}$ và $CC_{1}$; $L$ là giao điểm của $AI$ và $BC$

ta có $AI.AL=AC_{1}.AB=AP.AO \Rightarrow IPOL$ nội tiếp$\Rightarrow IP\perp AO(1)$

Gọi giao điểm của $AM$ và $(AC_{1}I)$ là $J\Rightarrow IJ\perp AJ$

Khi đó: $MJ.MA=MC_{1}.MB_{1}=MB.MC\Rightarrow J\in (ABC)$ 

giả sử $A'$ là giao điểm của $IJ$ với $(ABC)\Rightarrow AA'$ là đường kính của $(ABC)$

Từ đó dễ dàng chứng minh được $\overline{I;O;A}$

mà $JA'\perp AM$ nên $OI\perp AM$

Kết hợp với $AI\perp BC$ ta suy ra $I$ là trực tâm của $\Delta AOM\Rightarrow MI\perp AO(2)$

Từ $(1)$ và $(2)\Rightarrow \overline{M;I;P}\Rightarrow$ đpcm

Bài 81(APMO):

Cho tam giác $ABC$; đường cao $AD;BE;CF$ và $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Chứng minh rằng $OA;OB;OC;OD;OE;OF$ chia tam giác $ABC$ thành $3$ cặp tam giác bằng nhau.

Bài 1:

Phương trình ban đầu tương đương

$(x+y-1)(x^2-xy+y^2)=43xy$

Vì $x^2-xy+y^2\geq xy$ nên $x+y-1\leq 43$

Nếu $x+y-1=43\Rightarrow x^2-xy+y^2=xy\Rightarrow x=y=22$

Nếu $x+y-1<43$

 Đặt $d=gcd(x;y); x=dx'; y=dy'; (x';y')=1$, từ đó suy ra $(x+y-1)(x'^2-x'y'+y'^2)=43x'y'$

 mà $gcd(x'^2-x'y'+y'^2;x'y')=1$ (do $(x';y')=1$) và $x+y-1<43$ nên $x'^2-x'y'+y^2=43(1)$ và $d(x'+y')-1=x'y'(2)$

 Biến đổi phương trình $(1)$ thành $3(x'-y')^2+(x'+y')^2=172$

 Từ đó ta tính được $x';y'$ rồi thay vào $(2)$ tính $d$ để tìm nghiệm của phương trình