LTBN

 

Bài 9: 

Cho $\Delta ABC$ thoả mãn $AB-BC=\frac{AC}{\sqrt{2}}$ có $M$ là trung điểm của $AC$, $BN$ là phân giác trong. Chứng minh rằng $\widehat{BMC}+\widehat{BNC}=90^\circ$.

 

Kẻ phân giác ngoài BP của tam giác ABC.

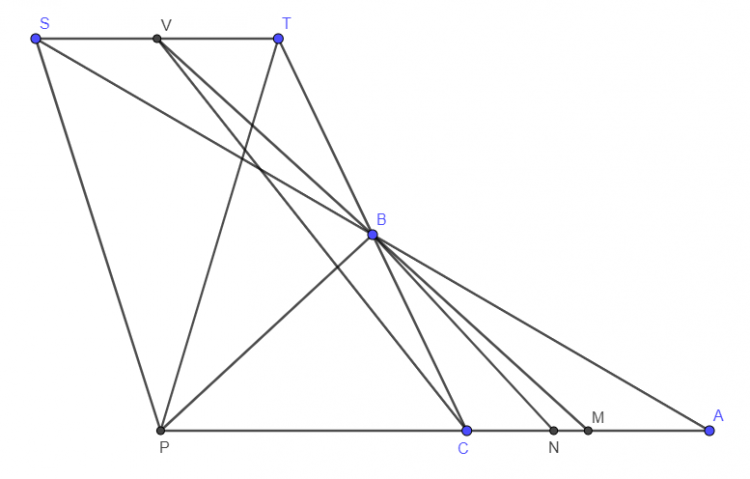
Gọi S, V, T lần lượt đối xứng với A, M, C qua B. Dễ thấy $S,V,T$ thẳng hàng và ST // BC.

Dễ thấy AB > BC nên C nằm giữa A, P.

Theo tính chất đường phân giác ngoài trong tam giác ta có $\frac{PA}{BA}=\frac{PC}{BC}=\frac{PA-PC}{BA-BC}=\frac{AC}{AC:\sqrt{2}}=\sqrt{2}$.

Do đó $CP^2=CB.CT\Rightarrow \Delta CBP\sim\Delta CPT\Rightarrow \frac{PT}{BP}=\frac{CP}{CB}=\sqrt{2}$.

Chứng minh tt ta có $\frac{PS}{BP}=\sqrt{2}$ nên $PS=PT$.

Từ đó $PV\perp ST$ nên tam giác PVM vuông tại P.

$\Rightarrow BP=BM\Rightarrow \widehat{BMC}+\widehat{BNC}=\widehat{BMC}+90^o-\widehat{BPM}=90^o$.

Ta có $p|n^3-1=(n-1)(n^2+n+1)$ nên $p|n-1$ hoặc $p|n^2+n+1$.

Dễ thấy $p-1\vdots n\Rightarrow p-1\geq n\Rightarrow n-1\leq p-2<p$.

Do đó $n-1$ không chia hết cho $p$.

Suy ra $n^2+n+1\vdots p$.

Do $p-1\vdots n$ nên đặt $p=nk+1$.

Ta có $n^2+n+1\vdots nk+1\Rightarrow n^2+n-nk\vdots nk+1\Rightarrow n+1-k\vdots nk+1$ (Do $(n,nk+1)=1$)

Xét 3 trường hợp:

+) $n+1-k>0$: Khi đó $n+1-k\geq nk+1\Rightarrow (n+1)(k-1)\leq -1$. (vô lí)
+) $n+1-k<0$: Khi đó $k-n-1\geq nk+1\Rightarrow (n-1)(k+1)\leq -3$. (vô lí)

+) $n+1-k=0$: Khi đó $p=n(n+1)+1$ nên $4p-3=(2n+1)^2$.

Vậy...

$\boxed{25}$: Cho tam giác $ABC$ có trực tâm $H$. $P$ là một điểm bất kì nằm trên cung $BC$ không chứa $A$. Gọi $P'$ là điểm đối xứng của $P$ qua $BC$. Đường tròn ngoại tiếp $\triangle OPP'$ cắt $AP$ tại $G$. Chứng minh trực tâm của tam giác $AGO$ nằm trên $HP'$.  

Giả sử $(O)$ là $(ABC)$.

$(OPP')$ cắt lại $(O)$ tại $F$.

Ta có $\angle FOG=\angle FPG=\frac{\angle FOA}{2}$ nên OG là phân giác của $\angle FOA$.

Suy ra A, F đối xứng với nhau qua OG.

Gọi E là trực tâm $\Delta AGO$ thì A, E, F thẳng hàng.

Gọi $D$ là điểm đối xứng với H qua BC.

Ta có $(P'O,P'E)\equiv (GO,GE)\equiv (AE,AO)\equiv \frac{\pi}{2}+(GO,AO)\equiv \frac{\pi}{2}+(GO,GA)+(AG,AO)\equiv \frac{\pi}{2}+(P'O,P'P)+(AP,AO)\equiv (P'O,BC)+\frac{\pi}{2}+\frac{(OP,OA)}{2}\equiv (P'O,BC)+\frac{\pi}{2}+(DP,DA)\equiv (P'O,BC)+(DP,BC)\equiv (P'O,BC)+(BC,HP')\equiv (P'O,HP')(\mod\pi)$.

Vậy E, H, P' thẳng hàng.

Cho các số thực dương thỏa mãn $a + b, ab$ là các số nguyên dương và $[a^2 + ab] + [b^2 + ab]$ là số chính phương với $[x]$ là phần nguyên của số thực $x$. Chứng minh rằng $a, b$ là các số nguyên.

Có $(a+b)^2\leq a^2+ab+b^2+ab\leq [a^2+ab]+[b^2+ab]< a^2+ab+1+b^2+ab+1=(a+b)^2+2$.

Do $(a+b)^2$ là số nguyên và $(a+b+1)^2>(a+b)^2+2$ nên $a^2+ab;b^2+ab$ là các số nguyên hay $a(a+b)\in mathbb Z;b(a+b)\in\mathbb Z$.

Do đó $a,b$ là các số hữu tỉ.

Đặt $a+b=m;ab=n(m,n\in \mathbb Z)$ thì $a,b$ là nghiệm hữu tỉ của đa thức $x^2-mx+n$.

Mặt khác hệ số cao nhất là 1 nên nếu đa thức trên có nghiệm hữu tỉ thì nghiệm đó cũng nguyên.

Vậy $a,b\in\mathbb Z$.

Tiếp ngày kiểm tra thứ 2   
$\boxed{23}$ Cho hình bình hành $ABCD$, đường thẳng qua $A$ vuông góc với $BD$ cắt $CD$, $CB$ tại $E$, $F$. Gọi $P$ đối xứng với $E$ qua $D$, $Q$ đối xứng với $F$ qua $B$. Các đường thẳng qua $A$, $P$, $Q$ theo thứ tự vuông góc với $AE$, $CD$, $CB$ cắt nhau tạo thành $\Delta XYZ$. Chứng minh $(XYZ)$ tiếp xúc với $(CDB)$.

(CEF) cắt (CBD) tại G.

Gọi H là giao của EF với BD.

Ta có $\angle GFE=\angle GCE=\angle GBH\Rightarrow (GFBH)$. 

Do đó $\angle BGF=90^o$. Tương tự $\angle DGE=90^o$.

Gọi T đối xứng với A qua B.

Có $\Delta ADE\sim\Delta FBA$ nên $FT||AP$. Mà $FT||AQ$ nên $A,P,Q$ thẳng hàng.

Dễ thấy $\Delta GDE\sim\Delta GBF$ nên $\angle PGD=\angle QGB$. Do đó $\angle PGQ=\angle DGB=\angle PCQ$ nên $P,G,C,Q$ đồng viên.

Từ đó $\Delta GPQ\sim\Delta GDB$. Mà $\frac{AP}{AQ}=\frac{PD}{AB}=\frac{ED}{AB}=\frac{DH}{BH}$ nên $\angle PGA=\angle DGH=\angle DEH$. Suy ra $G\in (PEA)$. Từ đó $G\in (PEAY)$.

Do đó $\angle YGE=90^o=\angle DGE$ nên $G,D,Y$ thẳng hàng. Tương tự G, B, Z thẳng hàng.

Mặt khác dễ thấy Y, G, C, Z đồng viên nên $G\in (XYZ)$. Mà $BD||YZ$ nên (GXYZ) tiếp xúc với (GBCD). (đpcm)

Bài 6: [IMO 1963] Chứng minh rằng: $cos \frac{\pi}{7}-cos \frac{2\pi}{7}+cos \frac{3\pi}{7}=\frac{1}{2}$

Xét $\Delta ABC$ có $\angle C=\frac{4\pi}{7};\angle B=\frac{\pi}{7};\angle A=\frac{2\pi}{7}$. Đặt $BC=a;CA=b;AB=c$.

Dựng D thuộc cạnh AB sao cho BD = CD. Khi đó dễ thấy $\Delta CDA$ cân tại C nên $BD=CD=AC$.

Dựng E thuộc cạnh AB sao cho BC = BE.

Ta có $\Delta CDB$ cân tại $D$ nên $\cos\frac{\pi}{7}\cos\widehat{CBD}=\frac{1}{2}\frac{BC}{BD}=\frac{a}{2b}$.

$\Delta CDA$ cân tại $C$ nên $\cos\frac{2\pi}{7}=\cos\widehat{CAD}=\frac{1}{2}\frac{AD}{AC}=\frac{c-b}{2b}$.

$\Delta BCE$ cân tại $B$ nên $\cos\frac{3\pi}{7}=\cos\widehat{BCE}=\frac{1}{2}\frac{CE}{BC}=\frac{1}{2}\frac{AC}{AB}=\frac{b}{2c}$. (Vì $\Delta ACE\sim\Delta ABC$)

Do đó ta chỉ cần chứng minh $\frac{a}{b}-\frac{c-b}{b}+\frac{b}{c}=1\Leftrightarrow ca=c^2-b^2\Leftrightarrow b^2=c(c-a)\Leftrightarrow AC^2=AE.AB$. (đúng)

Vậy $\cos\frac{\pi}{7}-\cos\frac{2\pi}{7}+cos\frac{3\pi}{7}=\frac{1}{2}$

Tìm các đa thức P(x) thỏa mãn đk:

$P(x)P(y)=P^2(\frac{x+y}{2})-P^2(\frac{x-y}{2})$ (1)

với mọi x,y$\epsilon R$

P.S: cho mik hỏi $P^2(x)$ với $(P(x))^2$ có giống nhau ko v

Nhận thấy $P(x)\equiv 0$ thoả mãn đk bài toán.

Ta xét trường hợp $P(x)\neq 0$.

Thay $x=0,y=0$ vào (1) ta được $P(0)=0$.

Với y = 3x thì $P(x).P(3x)=P^2(2x)-P^2(-x)$.

Hay $P(x).P(3x)+P^2(-x)=P^2(2x),\forall x\in\mathbb R$. (2)

+) Nếu $P(x)=c(c\neq 0)$ thì không thoả mãn.

+) Nếu $\deg P(x)=n\geq 1$:

Gọi hệ số cao nhất của $P(x)$ là $a_0\neq 0$. Từ (2) ta có $a_0(3^na_0)+a_0^2=()2^na_0)^2\Leftrightarrow 3^n+1=4^n\Leftrightarrow n=1$.

Do đó $P(x)=a_0x,a_0\in\mathbb R;a_0\neq 0$.

Thử lại đa thức này thoả mãn.

Vậy...

Kẻ tiếp tuyến tại A cắt OG tại H.

Dễ thấy tứ giác AHDG là hình bình hành nên OH = OG.

HG cắt (O) tại I, J (HI < HJ)

Xét dây IJ của (O) ta có dây cung AA (là tiếp tuyến tại A) và BC cắt IJ lần lượt tại H, G thoả mãn OH = OG nên theo định lí con bướm mở rộng của Sharygin ta có OE = OF.

Bài 3. (5,0 điểm)

 

Cho tam giác $ABC$, gọi $A_1\,,\,B_1\,,\,C_1$ lần lượt là các điểm đối xứng của $A\,,\,B\,,\,C$ qua $BC\,,\,CA\,,\,AB$

Chứng minh rằng   $A_1\,,\,B_1\,,\,C_1$  thẳng hàng khi và chỉ khi  $cosA\,cosB\,cosC\,\,=\,\,-\frac{3}{8}$

 

Câu hình chủ yếu là bổ đề trong sách NVL

Gọi $H$ là trực tâm tam giác ABC.

Gọi $O$ là tâm $(ABC)$.

Xét phép vị tự tâm O tỉ số 2.

$H^2_O: \mapsto X,B\mapsto Y,C\mapsto Z$.

Gọi $O_a$ là tâm của $(BHC)$. Khi đó $O,O_a$ đối xứng với nhau qua $BC$. Suy ra $O_a\in YZ$. Hiển nhiên $A_1\in (O_a)$ nên $YZ$ là trung trực của $HA_1$, hay $A_1$ là điểm đối xứng của $H$ qua $YZ$.

Tương tự $B_1,C_1$ lần lượt là điểm đối xứng của $H$ qua $ZX,XY$. Suy ra $A_1,B_1,C_1$ thẳng hàng khi và chỉ khi $H$ nằm trên $(XYZ)$, hay $OH=2R$.

Khi đó dễ thấy $H$ nằm ngoài $\Delta ABC$. Giả sử $\angle BAC> 90^o$. HA cắt BC tại D, cắt (O) lại tại E. 

Ta có $3R^2=OH^2-R^2=\wp_{H/(O)}=HA.HE=2HA.HD=2HA^2.\frac{HA}{HD}=8OM^2.\frac{HA}{HB}.\frac{HB}{HD}=8OM^2.\frac{-cosBAC}{cos ABC}.\frac{1}{cos ACB}=8OB^2.cos^2BAC.\frac{-cosBAC}{cos ABC}.\frac{1}{cos ACB}=8R^2.\frac{-1}{cosBACcosABCcosACB}\Rightarrow đpcm$.

Bài 2. (5,0 điểm)

 

Cho $n$ là số nguyên dương chẵn, có tổng các ước nguyên dương của nó là số lẻ. Chứng minh rằng tổng các ước chính phương (nhỏ hơn $n$) của $n$ sẽ không nhỏ hơn $\frac{n}{4}$

Giả sử $n=2^a.p_1^{k_1}.p_2^{k_2}...p_x^{k_x}$ với $p_1,p_2,...,p_x$ là các số nguyên tố lẻ.

Theo công thức tính tổng các ước nguyên dương của n:

$\sigma(n)=\prod_{i=1}^{x}\frac{p_i^{k_i+1}-1}{p_i-1}.(2^{a+1}-1)$.

Do $\sigma(n)$ là lẻ nên $\frac{p_i^{k_i+1}-1}{p_i-1}$ là lẻ với mọi $i\in\overline{1,x}$.

Nếu tồn tại i sao cho $k_i$ là lẻ thì đặt $k_i=2m-1$. Ta có $\frac{p_i^{2m}-1}{p_i-1}=\frac{p_i^m-1}{p_i-1}.(p_i^m+1)$ là số chẵn. (vô lí)

Do đó $k_i$ là số chẵn $\forall i\in\overline{1,x}$.

Đặt $k_i=2h_i$ thì $n=2^a.p_1^{2h_1}...p_x^{2h_x}$.

+) a lẻ: Đặt $a=2t+1$ thì tổng các ước chính phương của n là $(2^0+2^2+...+2^{2t}).\prod_{i=1}^x(p_i^0+p_i^2+...+p_i^{2h_i})\geq 2^{2t}.p_1^{2h_1}.p_2^{2h_2}...p_x^{2h_x}\geq \frac{n}{2}$.

+) a chẵn: Khi đó a - 1 là lẻ. Dễ thấy tổng các ước chính phương của n lớn hơn hoặc bằng tổng các ước chính phương của $\frac{n}{2}$ nên không nhỏ hơn $\frac{n}{4}$.

Vâỵ ta có đpcm.

Bài 1:

a) Với n = 0 thì bđt trở thành đẳng thức.

Với n = 1 ta cần chứng minh: $\sum a^4+\sum ab\geq 6\Leftrightarrow \sum ab-2\sum a^2b^2\geq -3$

$\Leftrightarrow q-2q^2+4rp\geq -3$. (Với $p=a+b+c;q=ab+bc+ca;r=abc$)

+) Nếu $0\leq q\leq \frac{3}{2}$ thì $q-2q^2+4rp\geq q-2q^2=(q+1)(3-2q)-3\geq -3$.

+) Nếu $3\geq q\geq \frac{3}{2}$ thì theo bđt Schur ta có $rp\geq \frac{p^2(4q-p^2)}{9}=\frac{(2q+3)(2q-3)}{9}$.

Do đó ta chỉ cần cm $q-2q^2+4\frac{(2q+3)(2q-3)}{9}\geq -3\Leftrightarrow (q-3)(2q-3)\leq 0$. (luôn đúng)

Với $n\geq 2$: Có $\sum a^{4n}+\sum a^nb^n\geq \frac{(a^4+b^4+c^4+ab+bc+ca)^n}{6^{n-1}}\geq 6$.

b) Với $n=\frac{2}{3}$ ta cho $a\to 0;b,c\to \sqrt{\frac{3}{2}}$ thì bđt không đúng.

Cho $S$ là tập số thực thỏa: 
i/ $1 \in S$

ii/ $\forall a,b \in S, a-b \in S$ 

iii/ $a \in S, a \ne 0$ thì $\frac{1}{a} \in S$

Chứng minh rằng $\forall a,b \in S$ thì $ab \in S$.

- Giúp với ạ, em cảm ơn  

Với mọi $a\in S$ ta có:

$1-a\in S$ nên $1-a-1\in S$, suy ra $-a\in S$.

Do đó với mọi $a,b\in S$ ta có $a-b\in S\Rightarrow a-b-a-a\in S\Rightarrow -(a+b)\in S\Rightarrow a+b\in S$.

Với $a\neq \pm 1$ thì $\frac{1}{a+1}\in S;\frac{1}{a-1}\in S\Rightarrow \frac{1}{a-1}-\frac{1}{a+1}\in S\Rightarrow \frac{2}{a^2-1}\in S\Rightarrow \frac{a^2-1}{2}\in S\Rightarrow \frac{a^2-1}{2}+\frac{a^2-1}{2}\in S\Rightarrow a^2-1 \in S\Rightarrow a^2\in S$.

Do đó: $a,b\in S(a,b\neq 0)\Rightarrow a^2,b^2,(a-b)^2\in S\Rightarrow 2ab\in S\Rightarrow \frac{1}{2ab}\in S\Rightarrow \frac{1}{ab}\in S\Rightarrow ab\in S(đpcm)$.

Hình như thiếu giả thiết $a,b,c,d$ đôi một phân biệt?

Đặt A là biểu thức trên. Trước hết nhận thấy:

$A> \frac{a}{a+b+c+d}+\frac{b}{a+b+c+d}+\frac{c}{a+b+c+d}+\frac{d}{a+b+c+d}=1$.

Lại có $A<\sum\frac{a+c+d}{a+b+c+d}=3$.

Do đó $\sum\frac{a}{a+b}=2\Leftrightarrow \frac{b}{b+c}-\frac{b}{a+b}-\frac{d}{c+d}+\frac{d}{d+a}=0\Leftrightarrow \frac{b(a-c)}{(a+b)(b+c)}+\frac{d(c-a)}{(c+d)(d+a)}=0\Leftrightarrow \frac{(a-c)(b-d)(ac-bd)}{(a+b)(b+c)(c+d)(d+a)}=0\Leftrightarrow ac=bd$.

Giả sử $a+b+c+d=p$ là số nguyên tố.

Ta có $dp=d(a+b+c+d)=da+ac+dc+d^2=(a+d)(c+d)$.

Do đó $a+d$ hoặc $c+d$ chia hết cho p. Mà $0<a+d;c+d<p$ nên ta có điều vô lí.

Vậy...

[IMO 1989] Chứng minh rằng với mỗi số nguyên dương $n$, đều tồn tại $n$ số nguyên dương liên tiếp sao cho không có số nào trong chúng là một luỹ thừa của một số nguyên tố.

Chọn n số $(2n+2)!+2,(2n+2)!+3,...,(2n+2)!+(n+1)$.

Giả sử tồn tại $i\in\overline{2,n+1}$ sao cho $(2n+2)!+i$ là luỹ thừa của một số nguyên tố.

Nhận thấy nếu $i$ có nhiều hơn hai ước nguyên tố, chẳng hạn như $a,b$ thì $(2n+2)!+i\vdots a$ và $(2n+2)!+i\vdots b$, trái với giả sử.

Do đó i là luỹ thừa của một số nguyên tố. Đặt $i=p^k$ thì $(2n+2)!+i=p^k\left ( \frac{(2n+2)!}{i}+1 \right )$.

Vì tích trên là luỹ thừa của $p$ nên $\frac{(2n+2)!}{i}+1\vdots p$.

Mặt khác từ $1<2i\leq 2n+2$ nên $\frac{(2n+2)!}{i}\vdots 2i\Rightarrow 1\vdots p$. (vô lí)

Vậy trong n số tự nhiên liên tiếp trên không tồn tại số nào là luỹ thừa của một số nguyên tố.

Không mất tính tổng quát giả sử $x,y\geq 0$.

Từ giả thiết ta có $x^{2002}+y^{2002}\vdots 2003$. Mà $2003$ là số nguyên tố dạng $4k+3$ nên $x^{1001};y^{1001}\vdots 2003\Rightarrow x=2003x_1;y=2003y_1(x_1,y_1\in\mathbb N)$.

Khi đó $2003^{9}(x_1^4+y_1^4)=x_1^{2002}+y_1^{2002}$.

Tương tự suy ra $x_1=2003x_2;y_1=2003y_2(x_2,y_2\in\mathbb N)$

$\Rightarrow 2003^{1993}(x_2^{2002}+y_2^{2002})=x_2^4+y_2^4$.

Dễ thấy $x_2=y_2=0$.

Vậy $x=y=0$.