Một bảng các ô vuông được điền bởi các số thực. Ở mỗi hàng và mỗi cột, tổng các số của hàng/cột đó là một số nguyên. Chứng minh rằng: mỗi số nguyên $x$ có thể thay bằng $\left \lceil x \right \rceil$ hoặc $\left \lfloor x \right \rfloor$ để tổng mỗi hàng/cột bằng tổng hàng/cột ban đầu.

Cho $m$ có ước nguyên tố lớn hơn $\sqrt{2m}+1$. Tìm số nguyên dương $M$ nhỏ nhất sao cho tồn tại $T$ là tập hữu hạn các số nguyên dương phân biệt thỏa mãn:

(i) $m$ và $M$ lần lượt là các phần tử nhỏ nhất và lớn nhất thuộc $T$

(ii) Tích các phần tử của $T$ là số chính phương

$\boxed{\text{Bài 5}}$ Các số $1,2,...,n^2$ được điền vào bảng kích thước nxn theo cách như hình vẽ bên dưới. Ta xóa đi n số từ bảng, sao cho không có hai số nào được xóa cùng hàng cũng như không có hai số nào được xóa cùng cốt. Tìm Tổng các số còn lại của bảng

Gọi $a_1,...,a_n$ là các số được xoá sao cho $a_i$ thuộc hàng thứ $i$

Vì $(i-1)n+1 \leq a_i \leq in$ nên nếu ta đặt $b_i=a_i-(i-1)n$, ta có $1 \leq b_i \leq n$

Vì các số được xoá không nằm cùng cột nên $a_i$ không đồng dư với $a_j$ mod $n$, với mọi $i \neq j$

Suy ra $b_i \neq b_j$

Vậy $b_1,...,b_n$ chính là hoán vị của các số $1,2,...,n$

Như vậy tổng $b_1+...+b_n=1+...+n=\frac{n^2+n}{2}$

$a_1+...+a_n=\frac{n\left ( n^2+1 \right )}{2}$

Tổng các số còn lại là: $\frac{n^2\left ( n^2+1 \right )-n\left ( n^2+1 \right )}{2}=\frac{n^4-n^3+n^2-n}{2}$

Cmr : \[C_n^k \] lẻ với mọi k\[ \in \left\{ {1,2,...,n} \right\}\] khi và chỉ khi n có dạng \[n = 2^m  - 1\]

Theo định lý Kummer, luỹ thừa của $2$ trong $C^k_n$ bằng số lần nhớ trong phép tính $n-k$ trong hệ cơ số $2$

Nếu $n=2^m-1$ thì $n=\overline{11..1}_2$ thì $n-k$ sẽ không có lần nhớ nào nên $C^k_n$ lẻ với mọi $k \leq n$

Nếu $n \neq 2^m-1$ thì trong biểu diễn nhị phân của $n$ có ít nhất một số $0$, vì vậy tồn tại $k \leq n$ để $n-k$ có ít nhất một lần nhớ, suy ra tồn tại $C^k_n$ chẵn

Ta có đpcm

$a_n$ là chữ số đầu tiên bên trái của số $2^n$, $b_n$ là chữ số đầu tiên bên trái của số $5^n$. Chứng minh rằng: bất kì $k$ số liên tiếp nào trong dãy $\left ( a_n \right )$ đều xuất hiện trong $k$ số liên tiếp của dãy $\left ( b_n \right )$

ta gọi một tập hợp các số nguyên dương C la tốt nếu với mọi số nguyên dương k tồn tại hai số a,b phân biệt trong C sao cho (a+k,b+k)>1 giả sử một tập tốt có tổng các phần tử là 2003.Cmr ta có thể loại một phần tử trong C sao cho tập còn lại vẫn tốt

Ta chứng minh bổ đề sau :

Bổ đề : $C$ là tập tốt khi và chỉ khi tồn tại  là số nguyên tố sao cho với mọi $i=\overline{0,p-1}$ , tồn tại $a,b\in C$, $a\equiv b\equiv i\left( \bmod p \right)$

Chứng minh :

Ta chứng minh phần đảo trước.

Giả sử tồn tại số nguyên tố $p$ sao cho $\forall i=\overline{0,p-1}$ ,$\exists {{a}_{i}},{{b}_{i}}\in C$ sao cho ${{a}_{i}}\equiv {{b}_{i}}\equiv i\left( \text{mod p} \right)$

$\forall k\equiv s\left( \text{mod p} \right)$ ,$s\in \left\{ 0,...,p-1 \right\}$ , đặt $a={{a}_{p-s}},b={{b}_{p-s}}$

Ta có : $\left( a+k,b+k \right)\vdots p\Rightarrow \left( a+k,b+k \right)>1$

Vậy $C$ là tập tốt

Ta chứng minh chiều ngược lại

Giả sử tồn tại tập tốt $C$ không thoả mãn điều kiện trên

Gọi $d$ là khoảng cách lớn nhất giữa $2$ phần tử trong $C$

Xét dãy số nguyên tố liên tiếp :

$2={{p}_{1}}<{{p}_{2}}<...<{{p}_{t}}\le d<{{p}_{t+1}}<...$

$\forall i=\overline{1,t}$ ,$\exists {{r}_{i}}$ trong hệ thặng dư đầy đủ modulo $p$ sao cho có nhiều nhất một phần tử thuộc $C$ đồng dư với $r_i$ modulo $p$.

Xét hệ phương trình đồng dư sau :

$x\equiv {{r}_{i}}\left( \text{mod }{{\text{p}}_{i}} \right)$ ,$\forall i=\overline{1,t}$

Theo định lí thặng dư Trung Hoa, tồn tại $k$ là nghiệm của hệ trên.

Xét $\left( a+k,b+k \right)$ ($a,b\in C$ )

Giả sử $a>b$

$\left( a+k,b+k \right)=\left( a-b,a+k \right)=1$ (vô lí) (vì $a+k$ không chia hết cho ,$\forall i=\overline{1,t}$ còn $a-b<p_{t+1}$

Suy ra đpcm

Quay lại bài toán:

Vì $C$ là tập tốt nên tồn tại số nguyên tố $p$ thoả mãn $\exists {{a}_{i}},{{b}_{i}}\in C,{{a}_{i}}\equiv {{b}_{i}}\equiv i\left( \text{mod p} \right)$ ,$\forall i=\overline{0,p-1}$

Xét $S=\sum\limits_{i=0}^{p-1}{{{a}_{i}}}+\sum\limits_{i=0}^{p-1}{{{b}_{i}}\equiv 2\left( 0+1+...+p-1 \right)\equiv p\left( p-1 \right)}\equiv 0\left( \text{mod p} \right)$

Dễ thấy $p<2003$

Vì $2003$ là số nguyên tố, $2003\ne S$

Suy ra tồn tại ít nhất một phần tử $a\in C,a\notin \left\{ {{a}_{i}},{{b}_{i}}\left| i=\overline{0,p-1} \right. \right\}$

Vậy tập $C-\left\{ a \right\}$ là tập tốt (đpcm)

http://diendantoanho...gồi-kề-chồng-c/

bạn vào đây xem sao nhé

Hai bài này khác nhau nhé bạn

gọi vị trí những nguoi dan ong : x_1,  x_2,..... x_n

                                   phu nu   :y_1, y₂,....y_n

 ban đầu ta có vị trí ngồi mà phụ nữ cạnh chồng : x₁y₁x₂y₂......x_ny_n. Ta tịnh tiến các vị trí của y :  y_ny₁y₂.....y_n-1

                                                                                                                                                                                                         y_n-1y₁y_2......y_n-2

                                                                                                                                                                                                        _{...............................}

vậy có n-1 cánh xếp

Bạn giải sai rồi nhé

Đáp số đúng là : $2n!\left [ n!-\sum_{i=1}^{n}\left ( -1 \right )^{i+1}\frac{2n}{2n-i}C_{2n-i}^{i}\left ( n-i \right )! \right ]$

Bài 43: Cho bảng ô vuông $n \times n$ được tô bằng $2$ màu trắng và đen. Giả sử tồn tại tập $A$ khác rỗng gồm các hàng sao cho bất kì cột nào cũng chứa một số chẵn ô trắng thuộc $A$. Chứng minh rằng: Tồn tại tập $B$ khác rỗng gồm các cột sao cho bất kì hàng nào đều có số chẵn ô trắng thuộc $B$.

Tại sao bài viết của em đôi khi lại bị xóa không có lý do!

Bài viết của bạn ở topic nào vậy

Bài 40: Cho $A$ là tập gồm $n$ phần tử, $A_1,...,A_m$ là các tập con có $3$ phần tử thoả mãn $\left | A_i \cap A_j \right |\leq 1, \forall i \neq j$. Chứng minh rằng: $\exists T \subset A$ thoả mãn: $\overline{\exists }$ $i$ sao cho $A_i\subseteq T,\left | T \right |\geq \left \lfloor \sqrt{2n} \right \rfloor$

Bài 41: Cho một bảng hình chữ nhật kích thước $2\times n$. Mỗi ô ta viết một số thực dương sao cho tổng $2$ số ở cùng cột đều bằng $1$. Chứng minh rằng: ta có thể bỏ mỗi cột một số sao cho tổng các số còn lại ở cùng một hàng không quá $\frac{n+1}{4}$

Cho $n \in \mathbb{N},n\geq 2$. Người ta xếp xung quanh $1$ chiếc bàn tròn theo chiều kim đồng hồ $2n$ chiếc ghế $g_{1},...,g_{2n}$. Hỏi có bao nhiêu cách xếp $n$ cặp vợ chồng ngồi vào $2n$ chiếc ghế thoả mãn:

i) Chồng không ngồi kề vợ.

ii) Hai người cùng giới không ngồi kề nhau.

$A$ là tập hợp các vectơ trong không gian $n$ chiều trên tập $\mathbb{Z}_3$ thoả mãn với mọi vectơ phân biệt $a,b \in A$, tồn tại toạ độ $i$ sao cho $b_i \equiv a_i+1\left ( mod 3 \right )$. Chứng minh rằng: $\left | A \right |\leq 2^n$

Lâu quá không đăng, topic đóng bụi dày cộm rồi

Bài 38: Gọi $f\left ( a,b,c \right )$ là số các cách để điền vão các ô trong bảng $a\times b$ bằng các số trong $\left \{ 1;2;...;c \right \}$ sao cho trong bất kì ô nào, số nằm trong ô đó đều lớn hơn hoặc bằng số ở ô trên nó và số ở ô bên trái nó. Chứng minh rằng: $f\left ( a,b,c \right )=f\left ( c-1,a,b+1 \right )$

Bài 39: Đặt $21$ điểm trên đường tròn. Chứng minh rằng: có ít nhất $100$ cặp điểm tạo ra cung nhỏ hơn hoặc bằng $120^0$

Bài 64: Chứng minh rằng các phần tử trong tập $\mathbb{N}$ có thể tô bằng $2$ màu thoả mãn điều kiện sau:

(i) Với mọi số nguyên tố $p$ và số tự nhiên $n$, các số $p^{n},p^{n+1},p^{n+2}$ không cùng một màu

(ii) Không tồn tại một dãy cấp số nhân vô hạn được tô cùng một màu

Bài 65: Chứng minh rằng: $\forall n \in \mathbb{Z}^+$, $n! \mid \prod_{k=0}^{n-1}\left ( 2^n-2^k \right )$

k phải tst,mà là imo shortlist hay sao day :v.hoặc bạn tìm ở vnmath.com có tài liệu "mot so bai toan so hoc lien quan den luy thua" cua pham van quoc

Bài toán IMO SL 2003 mà bạn nói là chứng minh tồn tại, còn bài trên là chứng minh vô hạn. Hai cái đó khác nhau nhé bạn

Cho $p$ là một số nguyên tố. Chứng minh rằng tồn tại vô hạn số nguyên tố $q$ sao cho với mọi số tự nhiên $n$, $n^p-p \not {\vdots} q$

không có đâu anh,nguyên thcs có đâu

Có trong cuốn này nè em

http://www.nhasachtr...o-hoc-tap-1.htm

 

THCS có dùng tổ hợp chập không anh!

Anh thấy mấy công thức tổ hợp chập có trong tài liệu chuyên toán lớp 6 đó em

Câu IV:
Cho tập hợp $A$ gồm 31 phần tử và dãy gồm $m$ tập hợp con của $A$ thỏa mãn đồng thời các điều kiện sau:
i) mỗi tập thuộc dãy $m$ có ít nhất 2 phần tử
ii) nếu hai tập thuộc dãy có chung nhau ít nhất 2 phần tử thì số phần tử của hai tập này khác nhau.
CMR $m\leq 900$

Nhận xét: số tập con của $A$ thuộc dãy có $n$ phần tử không quá
$\left \lceil \frac{C_{31}^{n}}{C_{29}^{n-2}} \right \rceil$
Ta chứng minh nhận xét trên bằng nguyên lý Dirichlet
Như vậy, ta có:
$m \leq \sum_{n=2}^{31}\left \lceil \frac{C_{31}^{n}}{C_{29}^{n-2}} \right \rceil=900$
Suy ra đpcm

Cho ba số thực dương $a,b,c$ thoả mãn: $\left \lfloor an \right \rfloor+\left \lfloor bn \right \rfloor=\left \lfloor cn \right \rfloor$

với mọi số tự nhiên $n$

Chứng minh rằng có ít nhất một trong ba số $a,b,c$ là số nguyên.

hix..hix...Bài mình chắc làm sai mất rồi 

Bài của thầy LNH lập luận logic và rất chặt chẽ mới thật là chính xác và đầy đủ...  

Mình mới lớp 10 thôi, không phải thầy

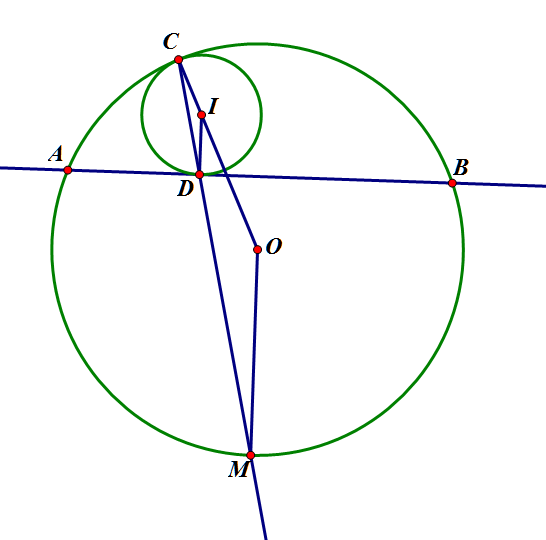
Cho hai đường tròn $(O), (I)$ và dây $AB$ của $(O)$ sao cho $(I)$ tiếp xúc trong với $(O)$ và tiếp xúc với $AB$.
Hãy dựng đường tròn $(J)$ sao cho $(J)$ tiếp xúc trong với $(O)$, tiếp xúc ngoài với $(I)$ và tiếp xúc với $AB$.

Ta giải bài này như sau:

Bổ đề 1: Cho đường tròn tâm $(O)$ và dây cung $AB$. Đường tròn tâm $(I)$ tiếp xúc trong với $(O)$ tại $C$ và tiếp xúc $AB$ tại $D$. Khi đó, $CD$ đi qua trung điểm $M$ của cung $AB$ không chứ $C$

Chứng minh:

Ta có: $\frac{CI}{CO}=\frac{ID}{OM}$

Theo hệ quả của định lí Thales, ta có $ID \parallel OM$

Mà $ID \perp AB$

Suy ra $OM \perp AB$ hay $M$ là trung điểm cung $AB$

Bổ đề 2: (Định lí Monge) Cho ba đường tròn $(I)$, $(J)$, $(K)$. Khi đó, ba tâm vị tự ngoài của hai trong ba đường tròn trên thẳng hàng

Việc chứng minh định lí trên khá đơn giản bằng Menelaus

Quay lại bài toán:

Xét 2 trường hợp:

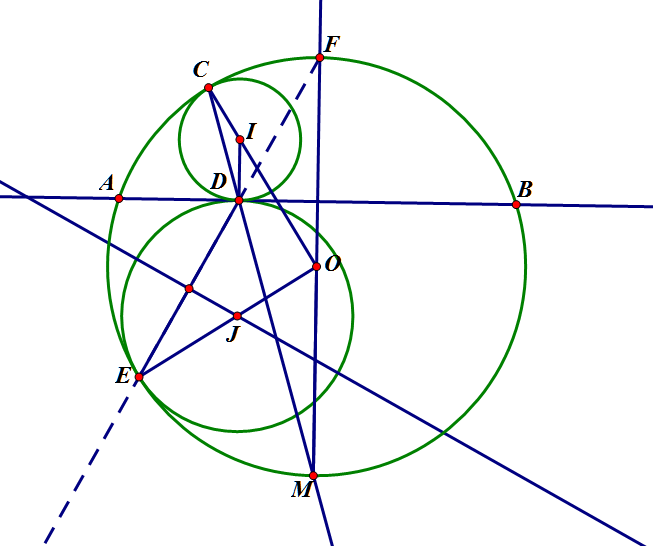
Trường hợp 1: $(J)$ nằm khác phía với $(I)$ bờ $AB$

$(I)$ và $(J)$ tiếp xúc ngoài nên sẽ có một tiếp tuyến chung trong

Vì $(I)$ và $(J)$ đều tiếp xúc $AB$ và nằm khác phía với $AB$ nên $AB$ là tiếp tuyến chung trong của hai đường tròn trên

Vậy $(J)$ cũng tiếp xúc $AB$ tại $D$

Gọi tiếp điểm của $(J)$ với $(O)$ là $E$, trung điểm cung $AB$ không chứa $E$ là $F$

Theo bổ đề 1, $E,F,D$ thẳng hàng

Vì vậy, ta có cách dựng sau:

$CD$ cắt $(O)$ tại $M$ khác $C$

$MO$ cắt $(O)$ tại $F$ khác $M$

$FD$ cắt $(O)$ tại $E$ khác $F$

Dựng đường trung trực của $ED$ cắt $OE$ tại $J$

Vẽ đường tròn tâm $J$ bán kính $JE$

Đây chính là đường tròn cần dựng

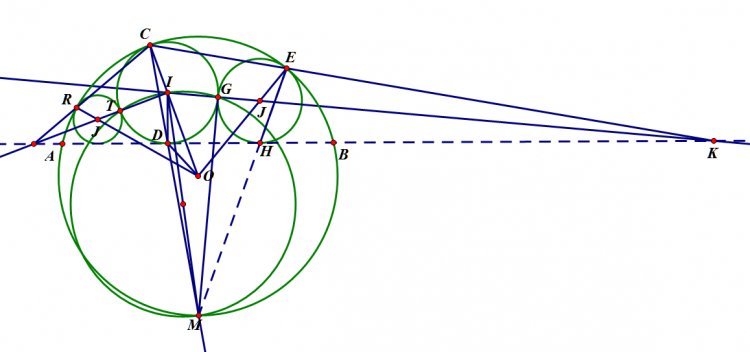
Trường hợp 2: $(J)$ nằm cùng phía với $(I)$ bờ $AB$

Gọi tiếp điểm của $(J)$ với $(O)$ và $AB$ là $E,H$, giao điểm của $IJ$ với $AB$ là $K$

Áp dụng bổ đề 2 cho ba đường tròn $(O)$, $(I)$, $(J)$, ta có $K,C,E$ thẳng hàng

Mặt khác, vì $M$ nằm trên trục đẳng phương của $(I)$ và $(J)$ (có thể chứng minh tứ giác $CDHE$ nội tiếp bằng biến đổi góc) nên nếu ta kẻ tiếp tuyến $MG$ của $(I)$, ta có $G$ cũng là tiếp điểm của $(J)$ khi tiếp xúc với $(I)$

Suy ra $I,G,K$ thẳng hàng

Như vậy điểm $K$ hoàn toàn có thể dựng được, từ đây ta có cách dựng sau:

Dựng trung điểm của $MI$

Vẽ đường tròn đường kính $MI$ cắt $(I)$ tại $G,T$

Dựng $K$ là giao điểm của $IG$ với $AB$

$KC$ cắt $(O)$ tại $E$ khác $C$

$ME$ cắt $AB$ tại $H$

Dựng đường trung trực của $HE$ cắt $OE$ tại $J$

Vẽ đường tròn $(J)$ bán kính $JE$

Đây chính là đường tròn cần dựng

Biện luận:

Ở trường hợp 1, vì các điểm xác định duy nhất nên ta có một nghiệm hình

Ở trường hợp 2, ta có 2 giao điểm của đường tròn đường kính $MI$ với $(I)$ nên có hai nghiệm hình

Kết luận:

Có thể dựng được ba đường tròn $(J)$ thoả mãn ycđb

Cho em làm lại bài của mình

Bài làm của toán thủ MO10-LNH

Gọi $x_1,x_2,x_3,x_4$ lần lượt là số kẹo ở mỗi phần

Không mất tính tổng quát, giả sử $x_1<x_2<x_3<x_4$

Đặt $x_i=x_{i-1}-s_i$, với $i=2,3,4$. Ta có:

$32=x_1+x_2+x_3+x_4=x_1+x_2+2x_3+s_4=x_1+3x_2+2s_3+s_4=4x_1+3s_2+2s_3+s_4$

Ta đưa bài toán từ tìm số bộ nguyên dương $\left ( x_1,x_2,x_3,x_4 \right )$ thành đếm số bộ nguyên dương $\left ( x_1,s_2,s_3,s_4 \right )$

Đặt $y_1=x_1-1$, $y_i=s_i-1$, $i=2,3,4$, ta có:

$y_1+2y_2+...+4y_4=22$

Ta có:

$y_1+2y_2+...+4y_4=22$

$y_1 \leq 22$, $y_2 \leq 11$, $y_3 \leq 7$, $y_4 \leq 5$

Số bộ nguyên không âm $\left ( y_1,y_2,y_3,y_4 \right )$ chính là hệ số của $x^22$ trong đa thức sau:

$P\left ( x \right )=(1+x^4+...+x^{20})(1+x^3+...+x^{21})(1+x^2+...+x^{22})(1+x+...+x^{22})$

$=\frac{\left ( x^{24}-1 \right )^3(x^{23}-1)}{\left ( x-1 \right )...(x^4-1)}$

$=\frac{(x^{23}-1)(x^{24}-1)(x^{12}+1)^2(x^6+1)(x^2-x+1)(x^8+x^4+1)}{(x-1)^2}$

$=(...+x^{22}-2 x^{21}+4 x^{20}-2 x^{19}+4 x^{18}-2 x^{17}+3 x^{16}-x^{15}+3 x^{14}-2 x^{13}+3 x^{12}-x^{11}+2 x^{10}-x^9+2 x^8-x^7+2 x^6-x^5+x^4+x^2-x+1)(1+2x+3x^2+...)$

$=(...+x^{22}-2 x^{21}+5 x^{20}-2 x^{19}+4 x^{18}-2 x^{17}+3 x^{16}-x^{15}+3 x^{14}-2 x^{13}+3 x^{12}-x^{11}+2 x^{10}-x^9+2 x^8-x^7+2 x^6-x^5+x^4+x^2-x+1)(1+2x+3x^2+...)$

Hệ số $x^{22}$ trong đa thức trên là $1\times 1-2\times 2+5\times 3-2 \times 4+4 \times 5-2 \times 6+3 \times 7-8+3 \times 9-2 \times 10+3 \times 11-12+2\times 13-14+2 \times 15-16+2 \times 17-18+19+21-22+23=136$

Vậy số cách chia kẹo thoả mãn yêu cầu đề bài là $136$

P/s: cuối cùng cũng xong

__________________________________

Điểm bài: $d=10$

Điểm thưởng $d_t=5$

Điểm mở rộng $d_{mr}=0$

Điểm thảo luận $d_{tl}=0$

$S = \left \lfloor\frac{52 - \left (t_{lb} - t_{rd} \right )}{3} \right \rfloor+3\times d+d_{mr}+d_{t}+d_{tl}=\left \lfloor\frac{52 - 16}{3} \right \rfloor+3\times 10 +0+5+0=47$

Bài làm của toán thủ MO10-LNH

Gọi $x_1,x_2,x_3,x_4$ là số kẹo ở mỗi phần và $x_1<x_2<x_3<x_4$

Ta có:

$0 \leq x_1-1 \leq x_2-2 \leq x_3-3 \leq x_4-4$

$x_1+x_2+x_3+x_4=32$

Đặt $y_i=x_i-i$,$i=\overline{1,4}$

Từ đây suy ra:

$y_1+y_2+y_3+y_4=22$ với $y_i \geq 0$

Theo bài toán chia kẹo Euler, ta có số cách chọn $y_1,y_2,y_3,y_4$ là $\binom{25}{3}$

Vậy số cách chia $32$ cái kẹo thành $4$ phần là $\binom{25}{3}$