Cho $ a,b,c> 0$ .CMR:
$ \frac{(a+b)^{2}}{a^{2}+b^{2}+2c^{2}}+\frac{(b+c)^{2}}{b^{2}+c^{2}+2a^{2}}+\frac{(c+a)^{2}}{c^{2}+a^{2}+2b^{2}}$$ \leq 3$

Anh Hân oi làm hộ em câu c vói , 2 hôm nũa thj HSG giỏi ồi

Cho $ a,b,c\geq 1$ . CMR :
$ abc+2(a^{2}+b^{2}+c^{2})+8\geq 5(a+b+c)$.
-----------------------------------------------------------------------------------
Bài này thục ra ĐK là $ a,b,c\geq 0$ thui , nhg nếu nhu thế thj` sẽ khó hon .
Ai có time thì CM thủ nhé !

1.cho a,b,c$\geq 1$.cmr
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{9}{2+abc}$

2.cho a+b+c $\epsilon [0,1]$,$a+b+c= \frac{3}{2}$.Chứng minh rằng
$a^{2}+b^{2}+c^{2}\leq \frac{5}{4}$

3.Cho x, y, z > 0 và xyz=32. Tìm Min của
S=$x^{2}+4xy+4y^{2}+2z^{2}$

4.Chứng minh rằng:$\frac{1}{a^{3}+1}+\frac{1}{b^{3}+1}+\frac{1}{c^{3}+1}\leq \frac{3}{2abc}$.Với$a,b,c\epsilon [0,1]$

Bài 4 :
Ta có : $ a^{3}+1= (a+1)(a^{2}-a+1)\geq (a+1)(2a-a)= a(a+1)$
$ \Rightarrow \sum \frac{1}{a^{3}+1}\leq \sum \frac{1}{a(a+1)}$ . Ta sẽ CM :$ \sum \frac{1}{a(a+1)}\leq \frac{3}{2abc}$
BĐT : $ \Leftrightarrow \sum \frac{bc}{abc(a+1)}\leq \frac{3}{2abc}\Leftrightarrow \sum \frac{bc}{a+1}\leq \frac{3}{2}$
Cái này đúng vì theo Mr.Cauchy thì :
$ \sum \frac{bc}{a+1}= \sum \frac{bc}{\sqrt{a+1}.\sqrt{a+1}}\leq \frac{1}{2}\sum (\frac{b^{2}}{a+1}+\frac{c^{2}}{a+1})\leq \frac{1}{2}\sum (\frac{b}{a+b}+\frac{c}{a+c})$
$ = \frac{1}{2} (\frac{b}{a+b}+\frac{c}{a+c}+\frac{a}{b+a}+\frac{c}{b+c}+\frac{a}{c+a}+\frac{b}{c+b})$
$ = \frac{1}{2}(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a})= \frac{3}{2}$
Vậy BĐT đc CM .

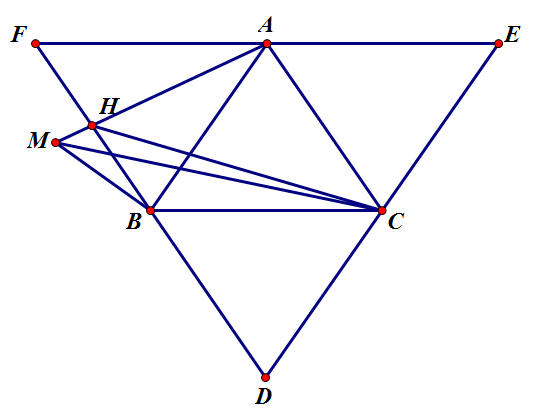
Bài 5.2:
Gọi X là tập hợp các điểm đã cho trước.
Trong các tam giác có 3 đỉnh thuộc tập X, ta chọn $\vartriangle ABC$ là tam giác có diện tích lớn nhất.
Các đường thẳng qua A,B,C thứ tự song song với BC,CA,AB đôi một cắt nhau tại D,E,F như hình vẽ.
Ta chứng minh mọi điểm của tập X đều nằm trong $\vartriangle DFE$, kể cả trên cạnh.
Giả sử, có 1 điểm M thuộc tập X sao cho M nằm ngoài $\vartriangle DFE$. Không mất tính tổng quát, giả sử vị trí của M nằm như hình vẽ.

Vẽ MA cắt FD tại H.
$S_{MAC}>S_{CAH}=S_{CAB}$: trái với cách chọn $\vartriangle ABC$ ban đầu.
Vậy ta có mọi phần tử của X đều nằm trong $\vartriangle DFE$ nên chúng nằm trong 1 trong 4 tam giác: ABC,ABF,ACE,BCD.
Theo nguyên lý Dirichlet, tồn tại 1 tam giác chứa 2012 điểm.
Lại có $S_{ABC}=S_{ABF}=S_{ACE}=S_{BCD}<1$ nên ta có đpcm.

Vùa thj sáng nay ! Mọi nguòi chém nhiệt tình vào !

Câu 1 (3 điểm )

1. Cho $ f(x)= \frac{x^{3}}{1-3x+3x^{2}}$ . Hãy tính giá trị của biểu thúc sau :

$ A= f(\frac{1}{2012})+f(\frac{2}{2012})+...+f(\frac{2010}{2012})+f(\frac{2011}{2012})$

2.Cho biểu thúc :
$ P=\frac{x-2\sqrt{x}}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x\sqrt{x}+x+\sqrt{x}}+\frac{1+2x-2\sqrt{x}}{x^{2}-\sqrt{x}}$
Tìm tất cả các giá trị của $ x$ sao cho giá trị của $P$ là một số nguyên.

Câu 2 (1,5 điểm )
Tìm tất cả các cặp số nguyên duong $ (x;y)$ thỏa mãn $\ (x+y)^{3}=(x-y-6)^{2}$.

Câu 3 (1,5 điểm )
Cho $\ a,b,c,d$ là các số thục thỏa mãn điều kiện :
$ abc+bcd+cda+dab= a+b+c+d+\sqrt{2012}$
CMR : $ (a^{2}+1)(b^{2}+1)(c^{2}+1)(d^{2}+1)\geq 2012$ .

Câu 4 (3 điểm )

Cho 3 đuòng tròn ($O_1$), ($O_2$) và ($O$) . Giả sủ ($O_1$) và ($O_2$) tiếp xúc ngoài vs nhau tại $I$ và cùng tiếp xúc trong vs ($O$) tại $M_1$ , $M_2$ . Tiếp tuyến của ($O_1$) tại $I$ cắt ($O$) tại $A$ , $A'$. $A$$M_1$ cắt lại ($O_1$) tại điểm $N_1$, $A$$M_2$ cắt lại ($O_2$) tại điểm $N_2$ .

1. CMR : tú giác $M_1$$N_1$$N_2$$M_2$ nội tiếp và $O$$A$ vuông góc vs $N_1$$N_2$.

2. Kẻ đuòng kính $P$$Q$ của ($O$) sao cho $P$$Q$ vuông góc vs $I$$A$ ( điểm $P$ nằm trên cung $A$$M_1$ ko chúa điểm $M_2$ ) .CMR : Nếu $P$$M_1$ và $Q$$M_2$ không song song thì $A$$I$, $P$$M_1$ và $Q$$M_2$ đồng quy .

Câu 5 ( 1 điểm )

Tất cả các điểm trên mặt phẳng đều đc tô màu , trong đó mỗi điểm đc tô bỏi 1 trong 3 màu xanh, đỏ, tím. CMR : luôn tồn tại ít nhất một tam giác cân, có 3 đỉnh thuộc các điểm của mặt phẳng mà 3 đỉnh của tam giác đó đôi một cùng màu hoặc khác màu .

Time : 150 phút
Ngày thi : 06/04/2012
Đề khó vật ! ! Chả biết các mem noi khác làm bài thế nào ?

Đề HP và VP năm nay khó đột ngột !

Cách khác câu 6:
Áp dụng BĐT Cauchy-Schwarz , ta có :
$3(ab+bc+ca)\leq (a+b+c)^{2}= [\frac{(a+b+c)2}{a+b+c}]\leq (\frac{a^{2}}{b}+\frac{b^{2}}{c}+\frac{c^{2}}{a})^{2}$
$=(\sum \frac{a^{2}}{b\sqrt{b(c+2a)}}.\sqrt{bc+2ca})^2\leq VT.3(ab+bc+ca)\Rightarrow VT\geq 1$

Cho $a+b+c=1$
$a$, $b$, $c$ $>0$
CMR:
$\sum \sqrt{\frac{ab}{c+ab}}\leq \frac{3}{2}$

Ta có :
$\sum \sqrt{\frac{ab}{c+ab}}= \sum \sqrt{\frac{ab}{c(a+b+c)+ab}}= \sum \sqrt{\frac{ab}{(c+a)(c+b)}}\leq \frac{1}{2}.\sum (\frac{a}{a+c}+\frac{b}{b+c})= \frac{3}{2}$

Với a,b,c là các số thực t/mđẳng thức a+b+c=0.CMR:
$2.(a^{5}+b^{5}+c^{5})=5abc(a^{2}+b^{2}+c^{2})$

Tù $a+b+c=0\Rightarrow a^{3}+b^{3}+c^{3}= 3abc$
$\Rightarrow (a^{2}+b^{2}+c^{2})(a^{3}+b^{3}+c^{3})= 3abc(a^{2}+b^{2}+c^{2})$
$\Leftrightarrow \sum a^{5}+\sum a^{3}(b^{2}+c^{2})= 3abc(a^{2}+b^{2}+c^{2})$ (1)
$a+b+c= 0\Leftrightarrow -a= b+c\Leftrightarrow a^{2}= b^{2}+c^{2}+2bc\Leftrightarrow b^{2}+c^{2}=a^{2}-2bc$
$(1)\Leftrightarrow \sum a^{5}+\sum a^{3}(a^{2}-2bc)= 3abc\sum x^{2}$
$(1)\Leftrightarrow \sum a^{5}+\sum a^{5}-2\sum a^{3}bc= 3abc\sum a^{2}$
$\Leftrightarrow 2\sum a^{5}= 3abc\sum a^{2}$ (đpcm )

Một bài vui vuj ! !
Cho $a,b,c$ là các số thục ko âm .
CMR : $2(a^{4}+b^{4}+c^{4})+4(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2})\geq 3ab(a^{2}+b^{2})+3bc(b^{2}+c^{2})+3ca(c^{2}+a^{2})$.

Câu 1.
Một học sinh có $18$ tờ giấy. Anh ta chọn ra một số tờ, sau đó cắt mỗi tờ trong số vừa chọn thành $18$ mảnh. Anh ta lại lấy một số mảnh và một lần nữa cắt mỗi mảnh thành $18$ mảnh. Anh ta cứ tiếp tục như thế cho đến khi mệt. Sau một thời gian, anh ta đếm lại và thấy có $2012$ mảnh. Chứng minh rằng học sinh đã sai trong quá trình kiểm đếm.

Câu 2.
Tìm tất cả các số có ba chữ số sao cho tổng bình phương các chữ số của nó bằng $90$.

Câu 3
Giả sử $a,b,c$ là độ dài ba cạnh của một tam giác và $m_a,m_b,m_c$ là độ dài các đường trung tuyến. Chứng minh rằng
$$ (m_{a}^{2} + m_{b}^{2} + m_{c}^{2}) = 3 (a^{2} + b^{2} + c^{2})$$

Câu 4.
Mỗi số hạng tiếp theo của dãy $1,0,1,0,1,0,...$ đều là chữ số hàng đơn vị của tổng $6$ số hạng liền trước nó. Chứng minh rằng trình tự $...0,1,0,1,0,1,...$ không bao giờ xảy ra trong dãy.

Câu 5
Chứng minh rằng phương trình sau có vô số nghiệm nguyên dương
\[ \frac{4}{n}=\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \]

Câu 1. Nhận thấy sau mỗi lần xé số mảnh giấy tăng lên 1 số là bội của $18-1=17$ nên tổng số giấy sẽ chia 17 du 1.
Mà 2012 chia 17 du 6 nên anh này đếm sai rồi !

Bài 3; here http://diendantoanho...showtopic=70046

Bài 344.
Với $a, b, c, d >0$ Chứng minh rằng :
$$\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge \dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}$$
Bài 345.
Cho $a, b, c \in [1.2]$ . Chứng minh rằng :
$$a^2(b+c)+b^2(c+a)+c^2(a+b)\le 7abc$$

Bài 345.
BĐT $\Leftrightarrow \frac{a(b+c)}{bc}+\frac{b(c+a)}{ca}+\frac{c(a+b)}{ab}\leq 7$
$\Leftrightarrow \frac{a}{c}+\frac{a}{b}+\frac{b}{c}+\frac{b}{a}+\frac{c}{a}+\frac{c}{b}\leq 7\Leftrightarrow (a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})\leq 10$
Đến đây bài này quen rồi !

Chuẩn bị một số bài, mong rằng tối nay mọi người sẽ có việc để thư giãn
Bài toán 3.
Cho $a,b,c$ là các số thực dương. Chứng minh rằng :
$$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge \dfrac{a^2+bc}{(a+b)(a+c)}+\dfrac{b^2+ca}{(c+a)(c+b)}+\dfrac{c^2+ab}{(c+a)(c+b)}$$

Bài toán 3.
BĐT $\Leftrightarrow \frac{\sum a(a+b)(a+c)}{(a+b)(b+c)(c+a)}\geq \frac{\sum (a^{2}+bc)(b+c)}{(a+b)(b+c)(c+a}$
$\Leftrightarrow \frac{\sum (a^{3}+a^{2}b+a^{2}c+abc)}{(a+b)(b+c)(c+a)}\geq \frac{\sum (a^{2}b+a^{2}c+b^{2}c+c^{2}b)}{(a+b)(b+c)(c+a)}$
$\Leftrightarrow \frac{\sum a^{3}+\sum ab(a+b)+3abc}{(a+b)(b+c)(c+a)}\geq \frac{2\sum ab(a+b)}{(a+b)(b+c)(c+a)}$
$\Leftrightarrow \sum a^{3}+\sum ab(a+b)+3abc\geq 2\sum ab(a+b)$
$\Leftrightarrow \sum a^{3}++3abc\geq \sum ab(a+b)$
( luôn đúng vì Schur )
MOD: Chỉ trích dẫn những chỗ cần thiết. Trích lại toàn bộ rất mất thẩm mỹ.

Cho 3 số dương a,b,c

$\frac{1}{b+c} + \frac{1}{c+a} + \frac{1}{a+b} \leq \frac{a}{a^{2}+bc} + \frac{b}{b^{2}+ca} + \frac{c}{c^{2}+ab}$

$\Leftrightarrow \sum (\frac{a}{a^{2}+bc}-\frac{1}{b+c})\geq 0\Leftrightarrow \sum \frac{ab+ac-a^{2}-bc}{(a^{2}+bc)(b+c)}\geq 0$
$\Leftrightarrow \sum \frac{(a-b)(a-c)}{(a^{2}+bc)(b+c)}\geq 0$
$\Leftrightarrow \frac{(a-b)(a-c)}{(a^{2}+bc)(b+c)}+\frac{(b-c)(b-a)}{(b^{2}+ac)(a+c)}+\frac{(c-a)(c-b)}{(c^{2}+ab)(a+b)}\geq0$
Dễ thấy : $\frac{1}{(a^{2}+bc)(b+c)}$ , $\frac{1}{(b^{2}+ca)(c+a)}$ , $\frac{1}{(c^{2}+ab)(a+b)}$
là 1 bộ đon điệu .
Do đó BĐT đúng theo BĐT Schur suy rộng ( vonicur schur ) .
-----
p/s : ko cảm thấy tụ tin vs lòi giải này lắm !

Chuẩn bị một số bài, mong rằng tối nay mọi người sẽ có việc để thư giãn
Bài toán 4.
Cho $a,b,c$ là các số thực dương thỏa mãn điều kiện $a+b+c+1=4abc$ . Chứng minh rằng :
$$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3 \ge \dfrac{1}{\sqrt{ab}}+\dfrac{1}{\sqrt{bc}}+\dfrac{1}{\sqrt{ca}}$$

Chúc mọi người có một buổi tối vui vẻ !

GT $\Leftrightarrow \frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}+\frac{1}{abc}= 4$
Đặt $\frac{1}{a}= x$ , $\frac{1}{b}= y$ , $\frac{1}{c}= z$ .
GT $\Leftrightarrow xy+yz+zx+xyz= 4$
Ta fải CM : $x+y+z\geq 3\geq \sqrt{xy}+\sqrt{yz}+\sqrt{zx}$
(*) CM : $x+y+z\geq 3$ .
Đặt $x+y+z= t$ .
Tù GT $\Rightarrow 4= xy+yz+zx+xyz\leq \frac{t^{2}}{3}+\frac{t^{3}}{27}\Leftrightarrow t^{3}+9t^{2}-108\geq 0\Leftrightarrow (t+6)^{2}(t-3)\geq 0$
$\Leftrightarrow t\geq 3$
(*) CM : $3\geq \sqrt{xy}+\sqrt{yz}+\sqrt{zx}$
Đặt $\sqrt{xy}= m,\sqrt{yz}= n,\sqrt{zx}= t\Rightarrow m^{2}+n^{2}+p^{2}+mnp= 4$
Thao nguyên tắc dirichlet Trong 3 số m,n,p có ít nhất 2 số cùng > hoặc < 1.
Giả su là m và n $\Rightarrow (m-1)(n-1)\geq 0\Leftrightarrow m+n\leq mn+1$ (1)
Mà $4=m^{2}+n^{2}+p^{2}+mnp\geq 2mn+mnp+p^{2}\Leftrightarrow 4-p^{2}\geq mn(2+p)$$\Rightarrow 2-p\geq mn\Leftrightarrow p\leq 2-mn$ (2)
Cộng (1) vs (2) đc ngay !
Tóm lại bài toán đc Cm hoàn toàn !
-----------
Hơi dài nhể !

Bam Ratatata Tatatatata Beat !
Bài 1 : Cho $x,y,z> 0$ . CMR : $\frac{xy}{z^{2}}+\frac{yz}{x^{2}}+\frac{zx}{y^{2}}+6\geq (x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$
Bài này tự chế !

Bài 2 : Cho $a,b,c> 0$ thỏa mãn $ab+bc+ca= 1$. CMR :
$\sqrt{a^{3}+a}+\sqrt{b^{3}+b}+\sqrt{c^{3}+c}\geq 2\sqrt{a+b+c}$


------------------
Wow , em yêu ảo lòi !

Nung nóng lại topic này nào.
-----------------
EXERCISE:
Cho a,b,c là các số thực dương. Chứng minh rằng:
$\left( {ab + bc + ca} \right)\left[ {{1 \over {{{\left( {a + b} \right)}^2}}} + {1 \over {{{\left( {b + c} \right)}^2}}} + {1 \over {{{\left( {c + a} \right)}^2}}}} \right] \ge {9 \over 4}$
--------------------

Cai' này là Iran 96 đúng ko nhi?

Bài 2, khai triển và bất đẳng thức trên quy về:
$\sum \frac{(z-x)(z-y)}{z^2}\geq 0$
Từ đây giả sử $x\leq y\leq z$
Thì bất đẳng thức trên đúng theo Schur suy rộng

Đây chính là BĐT Schur bậc -2

Cho 3 số dương x,y,z thỏa $x+y+z=6$. CMR
$x^2 +y^2 +z^2-xy-yz-zx+xyz\geq 8$

Đặt $ x+y+z=p$ , $ xy+yz+zx=q$ , $\ xyz=r$
$ BDT\Leftrightarrow p^{2}-3q+r\geq 8$ $ \Leftrightarrow 36-3q+r\geq 8\Leftrightarrow 28-3q+r\geq 0$
Ta sẽ CM :$28-3q+r\geq 0$ (1)
Tù BĐT quen thuộc : $ (x+y-z)(y+z-x)(z+x-y)\leq xyz$
Ta rút ra đc : $ r\geq \frac{4pq-p^{3}}{9}$ $ \Rightarrow r\geq \frac{8}{3}q+24$
Suy ra : $ VT\geq 28-3q+\frac{8}{3}q-24= 4-\frac{q}{3}$
Ta có BĐT quen thuộc : $ xy+yz+zx\leq \frac{(x+y+z)^{2}}{3}= 12\Rightarrow q\leq 12$
Do đó : $ VT\geq 4-\frac{q}{3}\geq 4-\frac{12}{3}= 0$
Suy ra : (1) đúng $\ \Rightarrow BDT$ đúng.
Dấu"=" xảy ra khi và chỉ khi $ x=y=z=2$ .

Tìm GTLN của biếu thức biết $x,y,z$ là các số thực dương và $x^2+y^2+z^2=xyz$
$$A=\frac{x}{x^2+yz}+\frac{y}{y^2+zx}+\frac{z}{z^2+xy}$$

GT $\Leftrightarrow \frac{x}{yz}+\frac{y}{zx}+\frac{z}{xy}= 1$
$A= \sum \frac{x}{x^{2}+yz}\leq\sum \frac{x}{4}.(\frac{1}{x^{2}}+\frac{1}{yz})= \sum \frac{1}{4}.(\frac{1}{x}+\frac{x}{yz})$
$= \frac{1}{4}.(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+\frac{x}{yz}+\frac{y}{zx}+\frac{z}{xy})= \frac{1}{4}.(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+1)$
Theo AM-GM : $\frac{x}{yz}+\frac{y}{zx}\geq \frac{2}{z}$
$\frac{y}{zx}+\frac{z}{xy}\geq \frac{2}{x}$
$\frac{z}{xy}+\frac{x}{yz}\geq \frac{2}{y}$
$\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq \frac{x}{yz}+\frac{y}{zx}+\frac{z}{xy}= 1$
$\Rightarrow A\leq \frac{1}{4}.(1+1)= \frac{1}{2}$
Dấu "=" khi $x=y=z=3$ .

[/right]

SOLUTION:
Áp dụng Cauchy-Schwarz dạng Engel:
$\sum {\frac{{{a^3}}}{{{b^2} + c}} = \sum {\frac{{{a^4}}}{{a{b^2} + ca}}} } \ge \frac{{{{\left( {\sum {{a^2}} } \right)}^2}}}{{\sum {a{b^2}} + \sum {ab} }} = \frac{1}{{\sum {a{b^2}} + \sum {ab} }}$
Và có: $\sum {ab} \le \sum {{a^2}} = 1$
Cần chứng minh: $\sum {a{b^2}} \le \frac{{\sqrt 3 }}{3}$
Đặt $x = a\sqrt 3 ;y = b\sqrt 3 ;z = c\sqrt 3 \to x,y,z > 0\& \sum {{x^2}} = 3$
Như vậy cần chứng minh:$\sum {x{y^2}} \le 3$
Ta có hệ quả quen thuộc sau:
Với x,y,z >0 thỏa $\sum {{x^2}} = 3$ thì:
$\sum {x{y^2}} \le xyz + 2$
Và áp dụng AM-GM: $\sum {{x^2}} \ge 3\sqrt[3]{{{{\left( {xyz} \right)}^2}}} \Rightarrow xyz \le 1$
=>$\sum {x{y^2}} \le 1 + 2=3$
=> $Q.E.D$
Đẳng thức xảy ra khi a=b=c$ = \frac{{\sqrt 3 }}{3}$
--------
P/S: Vì vội nên phải làm ngắn gọn, mọi người thông cảm nhé
--------

Tù đây có cách khác nhanh hon :
$(\sum xy^{2})^{2}= (\sum x.xy)^{2}\leq \sum x^{2}.\sum x^{2}y^{2}\leq \sum x^{2}.\frac{(\sum x^{2})^{2}}{3}= 9$
$\Rightarrow \sum xy^{2}\leq 3$

Do MSS22 không post đề đúng thời hạn nên BTC đưa ra đề dự bị như sau:
Với $x,y,z$ là các tham số dương cho trước, giải hệ pt sau trên tập số dương:
\[
\left\{ \begin{array}{l}
ax + by + cz = xyz \\
\sqrt {a + b} + \sqrt {a + c} + \sqrt {b + c} =x+y+z \\
\end{array} \right.
\]

Lâu ko vào MSS chém tj'

Tù pt đầu $\Rightarrow \frac{a}{xy}+\frac{b}{yz}+\frac{c}{zx}= 1$
$\Rightarrow \frac{a}{yz}+\frac{b}{zx}< 1\Leftrightarrow ax+by< xyz\Rightarrow z> \frac{a}{y}+\frac{b}{x}$
Tuong tụ : $x> \frac{b}{z}+\frac{c}{y}$ , $y> \frac{a}{z}+\frac{c}{x}$
Áp dụng BĐT AM-GM ta đc :
$2(x+y+z)> \frac{b}{z}+\frac{c}{y}+ \frac{a}{z}+\frac{c}{x}+\frac{a}{y}+\frac{b}{x}+x+y+z$
$= (\frac{a+b}{z}+z)+(\frac{b+c}{x}+x)+(\frac{c+a}{y}+y)$
$\geq 2( \sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a})$
$\Rightarrow x+y+z> \sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}$
Vì dấu "=" ko xảy ra nên mâu thuẫn vs PT thú 2 của hệ .
Vậy hệ PT đã cho vô nghiệm .

Bài giải chính xác. Chuẩn ko cần chỉnh
D - B = 24h
E = 10
F = 0
S = 54