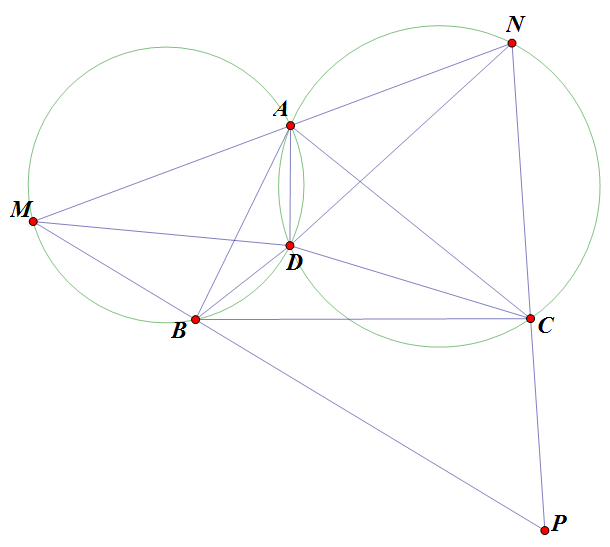
Dùng kiến thức hơi mạnh chút để giải tổng quát. Nếu ai thích thì có thể giải lại theo cách lớp 9 dựa vào cách này cũng được
Lời giải:

Chú ý các bộ điểm $(M,A,D,B);(N;A;D;C)$ đồng viên.
\[
\begin{array}{l}
\left( {PB;PC} \right) = \left( {PB;BD} \right) + \left( {BD;CD} \right) + \left( {CD;PC} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AD} \right) + \left( {DB;DC} \right) + \left( {AD;AN} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AN} \right) + \left( {DB;DC} \right) = \left( {DB;DC} \right)\left( {\bmod \pi } \right) \\
\end{array}
\]
Do đó, $D,B,P,C$ đồng viên hay quỹ tích $P$ là đường tròn ngoại tiếp $\vartriangle DBC$.

Cho em xài lại hình. Em không rõ thế này có được không.
Lời giải:
Thuận:
Ta có:
\[\widehat {MBD} + \widehat {NCD} = \widehat {MBD} + \left( {{{180}^o} - \widehat {DAN}} \right) = \widehat {MBD} + \widehat {MAD} = {180^o}\]
Do đó:
\[\widehat {DBP} + \widehat {DCP} = {360^o} - \left( {\widehat {MBD} + \widehat {NCD}} \right) = {180^o}\]
Vì thế $BDCP$ là tứ giác nội tiếp nên $P$ nằm trên đường tròn ngoại tiếp tam giác $BDC$
Đảo:
Lấy điểm P trên đường tròn ngoại tiếp tam giác $BDC$. $PB,PC$ cắt đường tròn ngoại tiếp tam giác $DAB,DAC$ tại $M,N$.
Ta có:
\[\widehat {MAD} = \widehat {PBD};\widehat {NAD} = \widehat {DCP}\]
Mà: $\widehat {PBD} + \widehat {DCP} = {180^o}$ nên $M,A,N$ thẳng hàng
Vậy quĩ tích của $P$ là ...

Cho $ABCD$ là tứ giác nội tiếp. Các điểm $P,Q,R$ lần lượt là chân các đường vuông góc hạ từ $D$ xuống các đường thẳng $BC,CA,AB$. CMR $PQ=QR$ khi và chỉ khi các đường phân giác của các góc $\angle ABC$ và $\angle ADC$ cắt nhau trên $AC$.

Đây chính là bài toán IMO lần thứ 44 năm 2003 mà.
Trích dẫn 1 lời giải trong THTT nhá.

Theo tính chất của đường thẳng Simpson ta có $P,Q,R$ thẳng hàng.
Trên tia đối của tia $DA$ lấy M sao cho $DM=DA$.
Theo tính chất phân giác:
\[ \text{E thuộc AC} \Leftrightarrow \frac{{AB}}{{BC}} = \frac{{DA}}{{DC}}\left( { = \frac{{AE}}{{EC}}} \right) \Leftrightarrow \frac{{AB}}{{BC}} = \frac{{DM}}{{DC}}\]
Mặt khác: $\widehat{ABC}=\widehat{MDC}$ (cùng bù với $\widehat{ADC}$)
Vì thế: $\triangle ABC$ đồng dạng $\triangle MDC \Leftrightarrow \left\{ \begin{array}{l}\widehat {ACB} = \widehat {MCD}\\\widehat {CAB} = \widehat {CMD}\end{array} \right.$
Mà tứ giác $AQDR$ nột tiếp nên $\widehat{DRQ}=\widehat{DAQ}$ và $\widehat{RDQ}=\widehat{CMD} \left( =\widehat{CAB} \right)$
$\Leftrightarrow \triangle DRQ$ đồng dạng $\triangle MAC \Leftrightarrow \frac{{RQ}}{{AC}} = \frac{{DR}}{{MA}} = \frac{{DR}}{{2.AD}} \text{ (1)}$
Dễ thấy rằng: $\triangle ADC \text{ đồng dạng } \triangle RDP$ nên luôn có: $\frac{{RP}}{{AC}} = \frac{{DR}}{{AD}} \text{ (2)}$
Từ $(1);(2)$ ta thấy ngay ĐPCM

Bài toán: Cho $a,b,c>0$. Chứng minh:
\[\frac{{\sqrt {2\left( {{a^2} + {b^2}} \right)\left( {{b^2} + {c^2}} \right)\left( {{c^2} + {a^2}} \right)} }}{{abc}} + \frac{{4(ab + bc + ca)}}{{{a^2} + {b^2} + {c^2}}} \ge 8\]

I can't help laughing =))

Bài toán: Cho $a,b,c\ge 0$. Chứng minh:

\[\sum\limits_{cyc} {\frac{{{a^2}}}{{{b^2} + {c^2}}}} \ge \sum\limits_{cyc} {\frac{a}{{b + c}}} \]

Lời giải:

Ta có:
\[\sum\limits_{cyc} {\frac{{{a^2}}}{{{b^2} + {c^2}}}} \ge \sum\limits_{cyc} {\frac{a}{{b + c}}} \Leftrightarrow \sum\limits_{cyc} {\left( {\frac{{{a^2}}}{{{b^2} + {c^2}}} - \frac{a}{{b + c}}} \right)} \ge 0\]
\[ \Leftrightarrow \sum\limits_{cyc} {\frac{{ab(a - b) - ca(c - a)}}{{({b^2} + {c^2})(b + c)}}} \Leftrightarrow \sum\limits_{cyc} {\left( {\frac{{ab(a - b)}}{{({b^2} + {c^2})(b + c)}} - \frac{{ab(a - b)}}{{({c^2} + {a^2})(c + a)}}} \right)} \ge 0\]
\[ \Leftrightarrow \sum\limits_{cyc} {\left[ {ab(a - b)\left( {\frac{1}{{({b^2} + {c^2})(b + c)}} - \frac{1}{{({c^2} + {a^2})(c + a)}}} \right)} \right]} \ge 0\]
\[ \Leftrightarrow \sum\limits_{cyc} {\left[ {ab(a - b).\frac{{{c^3} + {a^3} + {c^2}a + c{a^2} - {b^3} - {c^3} - {b^2}c - b{c^2}}}{{({b^2} + {c^2})({c^2} + {a^2})(b + c)(c + a)}}} \right]} \ge 0\]
\[ \Leftrightarrow \sum\limits_{cyc} {\left[ {ab(a - b).\frac{{(a - b)({a^2} + ab + {b^2}) + {c^2}(a - b) + (a - b)(ca + cb)}}{{({b^2} + {c^2})({c^2} + {a^2})(b + c)(c + a)}}} \right]} \ge 0\]
\[ \Leftrightarrow \sum\limits_{cyc} {\left[ {ab{{(a - b)}^2}.\frac{{{a^2} + {b^2} + {c^2} + ab + bc + ca}}{{({b^2} + {c^2})({c^2} + {a^2})(b + c)(c + a)}}} \right]} \ge 0\]

Bất đẳng thức cuối đúng nên ta có ĐPCM.

Dấu "=" xảy ra $ \Leftrightarrow \left[ \begin{array}{l}a = b = c\\\left\{ \begin{array}{l}a = b\\c = 0\end{array} \right. \text{ và các hoán vị}\end{array} \right.$

Bài 46: Cho tam giác $ABC$ có $3BC^2=2(AB^2+AC^2)$. $O$ là trung điểm $BC$. $H$ là trực tâm tam giác $ABC$. Chứng minh: $HA=HO$
___________________
Hàng tự chế chưa kiểm định chất lượng

Cho $a\neq b\neq c(a,b,c\in \mathbb{N})$
$P(a)=P(b)=P( c)=2$
Chứng minh: $P(x)-3=0$ không có nghiệm nguyên

Hình như thiếu điều kiện $x\in \mathbb{Z}$ thì $P(x) \in \mathbb{Z}$
Ta có $a,b,c$ là 3 nghiệm của phương trình $P(x)-2=0$.
Do đó ta có: $P(x)-2=(x-a)(x-b)(x-c).Q(x)$.
Đa thức $Q(x)$ thỏa điều kiện $x\in \mathbb{Z}$ thì $Q(x) \in \mathbb{Z}$ (cái này đơn giản)
Giả sử phương trình $P(x)-3=0$ có nghiệm nguyên thì:
$P(x)-2=1 \Leftrightarrow Q(x)(x-a)(x-b)(x-c)=1$.
Vì $a\ne b\ne c$ nên với $x$ nguyên thì vế trái có 3 ước khác nhau nhưng $VP=1$ nên mâu thuẫn
Vậy ta có ĐPCM

Tiện đây cho em hỏi là mình in ra là có đóng bìa như sách của NXB không hay chỉ in chay thành tập thôi ạ ?

Đó chắc là lí do vì sao mà hôm qua ở nhà em mưa khủng khiếp

Nhầm hàng rồi em. Thực ra đó là cơn bão điện từ mang theo những hạt điện tích. Bão này chỉ làm hư hại hệ thống điện tử thôi

bai 447:$x,y,z>0$cmr :$$\sqrt{x+y}+\sqrt{y+z}+\sqrt{x+z} \ge \frac{2}{\sqrt{3}}(x+y+z)$$

$(x;y;z)=(6;1;5)$ thì $VT<VP$ nên đề sai.

Áp dụng công thức Legendre (chả biết đúng tên chưa), ta có:
Số thừa số 5 trong phân tích tiêu chuẩn của $100!$ là:
\[\left\lfloor {\frac{{100}}{5}} \right\rfloor + \left\lfloor {\frac{{100}}{{{5^2}}}} \right\rfloor = 24\]

@nguyenta98: Chuẩn rồi đó
@hxthanh: Bài này phải hỏi là: "Chữ số đầu tiên khác không trong những chữ số tận cùng của $100!$ là số mấy?" như vậy hay hơn

Bài 24: Cho tam giác ABC nội tiếp đường tròn (O;R). C/m $AB^{2}+BC^{2}+CA^{2}\leq 9R^{2}$

Đại số hóa lên mà đánh.
Ta có các công thức sau:
\[S = \frac{{abc}}{{4R}} = \sqrt {p(p - a)(p - b)(p - c)} \]
Trong đó $a,b,c$ là độ dài $3$ cạnh tam giác và $p$ là nửa chu vi.
Từ công thức suy ra:
\[R = \frac{{abc}}{{4\sqrt {p(p - a)(p - b)(p - c)} }} = \frac{{abc}}{{\sqrt {(a + b + c)(a + b - c)(b + c - a)(c + a - b)} }}\]
Từ đó ta có bđt tương đương:
\[\frac{{9{a^2}{b^2}{c^2}}}{{(a + b + c)(a + b - c)(b + c - a)(c + a - b)}} \ge {a^2} + {b^2} + {c^2}\]
\[ \Leftrightarrow \left( {{a^2} + {b^2} + {c^2}} \right)(a + b + c)(a + b - c)(b + c - a)(c + a - b) \le 9{a^2}{b^2}{c^2}\]
Áp dụng phương pháp "nhân tung tóe" ta có bđt tương đương:
\[{a^6} + {b^6} + {c^6} + 3{a^2}{b^2}{c^2} \ge {a^2}{b^2}\left( {{a^2} + {b^2}} \right) + {b^2}{c^2}\left( {{b^2} + {c^2}} \right) + {c^2}{a^2}\left( {{c^2} + {a^2}} \right)\]
Dễ thấy đây chính là bđt $Schur$.
Vậy ta có ĐPCM.
Dấu "=" xảy ra $\Leftrightarrow a=b=c \Leftrightarrow \triangle ABC$ đều

2/Em nhận được rồi mà có lẽ không đi được vì hè này em bận.

Show hàng tên daovuquang tí Hắn chả có ảnh nào nên lấy cái trên mạng chụp hắn thi APMOPS vậy =))
Thằng đứng ngoài cùng bên trái ) =)) ko nhìn rõ mặt cho lắm =))

10 thằng có 9 thằng đeo "đít chai" =)))

Đề hiệp 3
Giải và biện luận hệ phương trình sau theo tham số thực $a$
\[
\left\{ \begin{array}{l}2x\left( {y^2 + a^2 } \right) = y\left( {y^2 + 9a^2 } \right) \\2y\left( {z^2 + a^2 } \right) = z\left( {z^2 + 9a^2 } \right)\\2z\left( {x^2 + a^2 } \right) = x\left( {x^2 + 9a^2 } \right) \\ \end{array} \right.
\]

Lời giải:

Từ phương trình đầu suy ra:
$2x=\frac {y(y^2+9a^2)}{y^2+a^2}=\frac{y^3+9a^2y}{y^2+a^2} \text{ (1)}$

Tương tự: $2y=\frac{z^3+9a^2z}{z^2+a^2} \text{ (2)}$ và $2z=\frac{x^3+9a^2x}{x^2+a^2} \text{ (3)}$

Không mất tính tổng quát ta giả sử $x=max\begin{Bmatrix}x,y,z\end{Bmatrix}$.

Từ $(3);(1)$ suy ra:
$2(z-x)=\frac{x^3+9a^2x}{x^2+a^2}-\frac{y^3+9a^2y}{y^2+a^2}$
$=\frac{(x^3y^2+x^3a^2+9a^2xy^2+9a^4x)-(x^2y^3+y^3a^2+9a^2x^2y-9a^4y)}{(x^2+a^2)(y^2+a^2)} \text{ (4)}$.

Xét tử của vế phải của đẳng thức (4), ta có:
$(x^3y^2+x^3a^2+9a^2xy^2+9a^4x)-(x^2y^3+y^3a^2+9a^2x^2y-9a^4y)$
$=x^2y^2(x-y)+a^2(x^2+xy+y^2)(x-y)-9a^2xy(x-y)+9a^4(x-y)$
$=(x-y)[x^2y^2+a^2(x^2-8xy+y^2)+9a^4]=(x-y)[(x^2y^2-6a^2xy+9a^4)+a^2(x^2-2xy+y^2)=(x-y)[(xy-3a)^2+a^2(x-y)^2]$.

Lúc này, thế vào (4) ta lại được:
$2(z-x)=\frac{(x-y)[(xy-3a)^2+a^2(x-y)^2}{(x^2+a^2)(y^2+a^2)}$

Để ý rằng $x \ge z$ do $x=max\begin{Bmatrix}x,y,z\end{Bmatrix}$ nên $2(z-x) \le 0$ và $ (xy-3a)^2+a^2(x-y)^2 \ge 0$ , $(x^2+a^2)(y^2+a^2)>0$.

Do đó: $x-y \le 0 \to x \le y$, mà $x=max\begin{Bmatrix}x,y,z\end{Bmatrix} \to x=y$.

Do đây là hệ hoán vị vòng quanh nên từ đó ta suy ra $x=y=z$.

Từ $x=y$ thế vào phương trình đầu tiên của hệ, ta được:
$2x(x^2+a^2)=x(x^2+9a^2)$.

Dễ thấy phương trình trên có 1 nghiệm $x=0$.

Với $x$ khác 0 ta tìm được $x=\sqrt {7}a$ hoặc $x=-\sqrt {7}a$

Suy ra: $x=y=z=0$ hoặc $x=y=z=\sqrt{7}a$ hoặc $x=y=z=-\sqrt{7}a$

Vậy hệ phương trình có 3 nghiệm $(x;y;z) = (0;0;0);(\sqrt {7}a;\sqrt {7}a;\sqrt {7}a);(-\sqrt {7}a;-\sqrt {7}a;-\sqrt {7}a)$

Khi $a=0$ thì pt có nghiệm $x=y=z=0$
Nên em đã sai từ bước ban đầu khi chia mà ko xét $a=0$
Cho em 6đ là hên rồi đó =.="
D-B=35h
E=6
F=0
S=31

Bài 4 (bài này thiên về vật lý-quang học): Cho A,B cùng nằm trên nửa mặt phẳng xy. Xác định M trên xy sao cho MA+MB nhỏ nhất

Nói sơ thôi.
Nếu nhớ không lầm thì đây là 1 bài trong SGK toán 8 (bài gì gì đó mà có người gánh nước).
Dựng C đối xứng A qua xy. CB cắt xy tại điểm M cần tìm

Bài toán: Cho $a,b,c$ là các số không âm thỏa mãn $a+b+c=1$. Chứng minh:
\[\sqrt {a + {{(b - c)}^2}} + \sqrt {b + {{(c - a)}^2}} + \sqrt {c + {{(a - b)}^2}} \ge \sqrt{3}\]

Cho dãy $2012$ số nguyên dương $a_1;...;a_n$ thỏa tính chất sau: với mọi phần tử $a_i, a_j$ trong dãy mà $i<j-1$ thì tồn tại $a_k$ với $i<k<j$ sao cho $a_k \vdots BCNN(a_i;a_j)$. Tìm GTLN của số các giá trị khác nhau có trong dãy.

Em xin giải. Giờ mới thấy đề
Lời giải:
Ta có tính chất: bội số khác $0$ của một số nguyên dương a thì không nhỏ hơn $a$ $(*)$
Xét $i=m$;$j=m+2$ ($m\in [1;n-3]$) thì thỏa mãn điều kiện $j-1>i$.
Theo đề thì tồn tại phần tử $a_k$ trong dãy trên thỏa mãn $a_k \vdots BCNN(a_i;a_j)$ mà $i<k<j$.
Ta xét $i=m;j=m+2$ nên $m<k<m+2 \Rightarrow k=m+1$.
Áp dụng tính chất $(*)$ ta có: $a_k=a_{m+1}$ là bội của $BCNN(a_m;a_{m+2})$ nên $a_{m+1}\ge BCNN(a_{m+2},a_m)$.
Cũng từ $(*)$ suy ra $a_{m+1} \ge BCNN(a_m;a_{m+2}) \ge a_m$ và $a_{m+1} \ge BCNN(a_m;a_{m+2}) \ge a_{m+2}$ $(**)$
Do đó: $(**) \Rightarrow a_{m+1}\ge a_{m+2}$
Xét $i=m+1;j=m+3$ ta cũng có tính chất $(**)$: $a_{m+2} \ge BCNN(a_{m+1};a_{m+3}) \ge a_{m+1}$ và $a_{m+2} \ge BCNN(a_{m+1};a_{m+3}) \ge a_{m+3}$. Vì vậy: $a_{m+2}\ge a_{m+1}$
Do đó qua 2 lần xét như trên ta có: $a_{m+2} \ge a_{m+1}$ và $\Rightarrow a_{m+1}\ge a_{m+2}$
$\Rightarrow a_{m+1}=a_{m+2}$.
Cho $m$ chạy từ 1 đến $n-3$ ta có: $a_2=a_3=...=a_{2011}$.
Từ $(**)$ cũng suy ra $a_2\ge a_1$ và $a_{2011} \ge a_{2012}$.
Do đó: $a_2=a_3=...=a_{2011} \ge a_1$ và $a_2=a_3=...=a_{2011} \ge a_{2012}$
Do đó số phần tử nhiều khác nhau nhiều nhất của dãy là 3 khi và chỉ khi $a_1 \ne a_2=a_3=...a=_{2011} \ne a_{2012}$

Xét dấu = không đúng.
D-B=21.7h
E=9
F=0
S=53.3

ĐỀ THI TUYỂN SINH LỚP 10 CHUYÊN LÊ QUÝ ĐÔN - ĐÀ NẴNG

Bài 1: (2,0 điểm)

a) Cho phương trình $x^2-2(m-1)x-1=0$ ($m$ là tham số). Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt $x_1;x_2$ thỏa mãn: $|x_1-x_2|=2$
b) Lập phương trình bậc 2 nhận $x_1=y_1\sqrt{y_2}+3\sqrt{y_1}$ và $x_2=y_2\sqrt{y_1}+3\sqrt{y_2}$ là nghiệm với $y_1;y_2$ là nghiệm của phương trình $y^2-7y+1=0$

Bài 2: (2,5 điểm)

a) Giải hệ phương trình: $\left\{ \begin{array}{l}{x^2} = |x| + y\\{y^2} = |y| + x\end{array} \right.$
b) Giải phương trình:
\[x = \sqrt {40 - x} .\sqrt {45 - x} + \sqrt {45 - x} .\sqrt {72 - x} + \sqrt {72 - x} .\sqrt {40 - x} \]

Bài 3: (2,0 điểm)

a) Cho $x,y,z,t$ thỏa mãn $x^2+y^2+z^2+t^2\le 1$. Chứng minh:
\[\sqrt {{{(x + z)}^2} + {{(y - t)}^2}} + \sqrt {{{(x - z)}^2} + {{(y + t)}^2}} \le 2\]
b) Tìm $x,y \in \mathbb{N}$ thỏa mãn $\sqrt{x}+\sqrt{y}=\sqrt{2012}$

Bài 4: (2,5 điểm)
Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Biết AB,CD cắt nhau tại E; AD cắt BC tại F; AC cắt BD tại M. H là hình chiếu của M lên AB. CH cắt BD tại N.

a) Chứng minh: $\frac{{DB.MN}}{{DM.NB}} = 1$
b) Hai đường tròn ngoại tiếp các tam giác BCE và CDF cắt nhau tại điểm thứ 2 là L. Chứng minh: E,F,L thẳng hàng.

Bài 5: (1,0 điểm)
Cho tam giác ABC không đều có các cạnh $BC=a;CA=b;AB=c$. $I,G$ là tâm đường tròn nội tiếp và trọng tâm tam giác. Chứng minh nếu $IG \bot IC$ thì ta có $6ab=(a+b)(a+b+c)$

Bài toán: Cho các số nguyên dương $a,b,c,d,e$ thỏa mãn $1\le a<b<c<d<e$. Chứng minh rằng:
\[\frac{1}{{\left[ {a,b} \right]}} + \frac{1}{{\left[ {b,c} \right]}} + \frac{1}{{\left[ {c,d} \right]}} + \frac{1}{{\left[ {d,e} \right]}} \le \frac{{15}}{{16}}\]
__________________________________________
Kí hiệu $[a,b]$ là BCNN của $a,b$

Giải hệ phương trình:

$\left\{ \begin{array}{l}
3{a^3} = 3{b^2} + 3b + 1 \\
3{b^3} = 3{c^2} + 3c + 1 \\
3{c^3} = 3{a^2} + 3a + 1 \\
\end{array} \right.$

~~~

Tóm tắt:

Dễ thấy: $3a^3=3b^2+3b+1>0 \Rightarrow a>0$

Tương tự: $b,c>0$

Giả sử $a$ là số nhỏ nhất trong 3 số $a,b,c$ ta có.
$$3b^2+3b^2-3a^2-3a=3a^3-3c^3\le 0 \Rightarrow b\le a$$

Mà $a$ là số nhỏ nhất nên $b=a$.

Tương tự thế làm tiếp nhé bạn .....

Cho em bổ sung.
Nếu $x=y=0$ thì không thỏa điều kiện xác định.
Nếu $x=0$ hoặc $y=0$ thì $VT=1>\frac{5}{8}$
Nếu $x,y$ khác $0$ thì giải như trên

Bài 2: Cho các số không âm $x,y$. Chứng minh:
$$\frac{{{x}^{4}}+{{y}^{4}}}{{{\left( x+y \right)}^{4}}}+\frac{\sqrt{xy}}{x+y}\ge \frac{5}{8}$$

Ta có:
\[\frac{{{x^4} + {y^4}}}{{{{\left( {x + y} \right)}^4}}} + \frac{{\sqrt {xy} }}{{x + y}} \ge \frac{5}{8} \Leftrightarrow \frac{{\frac{{{x^4}}}{{{y^4}}} + 1}}{{{{\left( {\frac{x}{y} + 1} \right)}^4}}} + \frac{{\sqrt {\frac{x}{y}} }}{{\frac{x}{y} + 1}} \ge \frac{5}{8}\]
Đặt $t = \sqrt {\frac{x}{y}} $ thì $t>0$ và bất đẳng thức trở thành:
\[\frac{{{t^8} + 1}}{{{{({t^2} + 1)}^4}}} + \frac{t}{{{t^2} + 1}} \ge \frac{5}{8}\]
Qui đồng 2 vế ta có bất đẳng thức tương đương:
\[8\left[ {{t^8} + 1 + t{{\left( {{t^2} + 1} \right)}^3}} \right] \ge 5{\left( {{t^2} + 1} \right)^4}\]
\[ \Leftrightarrow 8\left[ {{t^8} + 1 + t\left( {{t^6} + 3{t^4} + 3{t^2} + 1} \right)} \right] \ge 5\left( {{t^8} + 4{t^6} + 6{t^4} + 4{t^2} + 1} \right)\]
\[ \Leftrightarrow 8\left( {{t^8} + {t^7} + 3{t^5} + 3{t^3} + t + 1} \right) - 5\left( {{t^8} + 4{t^6} + 6{t^4} + 4{t^2} + 1} \right) \ge 0\]
\[ \Leftrightarrow 3{t^8} + 8{t^7} - 20{t^6} + 24{t^5} - 30{t^4} + 24{t^3} - 20{t^2} + 8t + 3 \ge 0\]
\[ \Leftrightarrow \left( {3{t^8} - 3{t^7}} \right) + \left( {11{t^7} - 11{t^6}} \right) - \left( {9{t^6} - 9{t^5}} \right) + \left( {15{t^5} - 15{t^4}} \right) - \left( {15{t^4} - 15{t^3}} \right) + \left( {9{t^3} - 9{t^2}} \right) - \left( {11{t^2} - 11t} \right) - \left( {3t - 3} \right) \ge 0\]
\[ \Leftrightarrow (t - 1)\left( {3{t^7} + 11{t^6} - 9{t^5} + 15{t^4} - 15{t^3} + 9{t^2} - 11t - 3} \right) \ge 0\]
\[ \Leftrightarrow (t - 1)\left[ {\left( {3{t^7} - 3{t^6}} \right) + \left( {14{t^6} - 14{t^5}} \right) + \left( {5{t^5} - 5{t^4}} \right) + \left( {20{t^4} - 20{t^3}} \right) + \left( {5{t^3} - 5{t^2}} \right) + \left( {14{t^2} - 14t} \right) + \left( {3t - 3} \right)} \right] \ge 0\]
\[ \Leftrightarrow {(t - 1)^2}\left( {3{t^6} + 14{t^5} + 5{t^4} + 20{t^3} + 5{t^2} + 14t + 3} \right) \ge 0 \text{ (1)}\]
Ta có: $(t-1)^2\ge 0$ và ${3{t^6} + 14{t^5} + 5{t^4} + 20{t^3} + 5{t^2} + 14t + 3} \ge 0$ (vì $t>0$) nên bất đẳng $(1)$ luôn đúng. Do đó ta có điều phải chứng minh.
Dấu $"="$ xảy ra $ \Leftrightarrow t = 1 \Leftrightarrow \sqrt {\frac{x}{y}} = 1 \Leftrightarrow x = y$
_________________________________________
P/s: Hi vọng trọng tài chấm không trừ điểm chỗ phân tích nhân tử. Viết dài quá nên em tắt 1 tí

Thời gian nộp bài tính từ lúc nộp bài sửa chữa.
D-B=8.7h
E=10
F=0
S=69.3

Bài toán: Cho tam giác ABC. Hãy xác định các điểm $M,N,P$ lần lượt thuộc các cạnh $BC,CA,AB$ để chu vi tam giác $MNP$ nhỏ nhất.

1. Họ và tên:Cao Xuân Huy
2. Nick trên Diễn đàn: Cao Xuân Huy
3. Ngày sinh: 18/12/1997
4. Nghề nghiệp: Học sinh
5. Địa chỉ nhà: Cao Xuân Hoan. Chi cục kiểm dịch thực vật vùng III số 146, Hoàng Diệu, Q.Hải Châu, Đà Nẵng (Cho em xin lỗi vì nhà em không có địa chỉ cụ thể nên gửi địa chỉ bố em)
6. Mail/ Số điện thoại liên lạc: [email protected]
7. Địa điểm đăng kí tham gia: Đà Nẵng
8. Bạn có muốn tham gia vào BTC không: Không