Chủ đề này có 239 trả lời

[Uchiha sisui]

Hai bạn đừng spam nữa nhé loãng topic ở đây là đăng bài ko phải để tranh luận nếu có thắc mắc xin hãy trao đổi qua tin nhắn đừng nên đăng ở đây. 

Về việc bạn  Uchiha Sisui nhắc nhở các thành viên gửi kèm hình theo đó là việc không thể bắt buộc. Người khác tham gia đóng góp cho Topic đã là quý rồi việc họ đăng hình hay không là việc của họ mình không có quyền bắt buộc (Nội quy topic cũng không bắt buộc) tùy vào mỗi cá nhân thôi. Thầy Hùng không onl thường xuyên nên mình là người quản lí topic này. Nếu có thắc mắc xin vui lòng gửi qua tin nhắn mình sẽ giải đáp hoặc trao đổi lại với thầy Hùng sau.
Nhắc thêm Uchiha Sisui  em ghi nguồn vào các bài toán đề xuất nhé anh thấy em đăng vài bài mà không ghi nguồn. Nếu không biết hãy để sưu tầm

 

Bài toán đề xuất tiếp theo :

Bài 78:  (Czech-Slovak-Polish  2013)

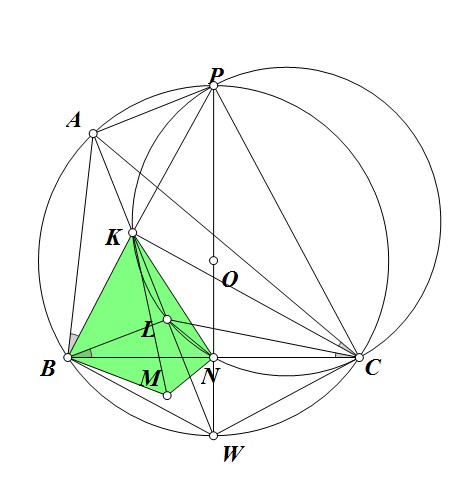
Cho tam giác $ABC$ nội tiếp $(O)$ .$P$ là điểm chính giữa cung có chứa điểm $A$ .$(X)$ là đường tròn đường kính $PC$ .$K,L$ lần lượt là giao điểm của phân giác trong góc $BAC$ với ($K$ gần $A$).$M$ là điểm đối xứng của $L$ qua $BC$ . Chứng minh đường tròn ngoại tiếp tam giác $BKM$ đi qua trung điểm của $BC$ .

AOPS.png

P/s: Chưa ai giải bài $74$ nhỉ? 

chắc bạn ảo tưởng bạn hơn tuổi mình? Hơn nữa bạn nói về việc ghi nguồn? bạn có nhầm , phiền bạn xem lại mỗi bài toán tôi đều có ghi trích từ đề thi nào đó, khi nhắc nhở ai đó nên xem lại mình ! Bạn hãy xem topic mà tôi muốn nói 

[Nguyenphuctang]

chắc bạn ảo tưởng bạn hơn tuổi mình? Hơn nữa bạn nói về việc ghi nguồn? bạn có nhầm , phiền bạn xem lại mỗi bài toán tôi đều có ghi trích từ đề thi nào đó, khi nhắc nhở ai đó nên xem lại mình ! Bạn hãy xem topic mà tôi muốn nói 

Vâng thưa bài 68,69,70 bạn không ghi nguồn. Tôi đề nghị đừng đăng lên đây có gì trao đổi riêng qua tin nhắn.

[NHoang1608]

Bài toán đề xuất tiếp theo :

Bài 78:  (Czech-Slovak-Polish  2013)

Cho tam giác $ABC$ nội tiếp $(O)$ .$P$ là điểm chính giữa cung có chứa điểm $A$ .$(X)$ là đường tròn đường kính $PC$ .$K,L$ lần lượt là giao điểm của phân giác trong góc $BAC$ với ($K$ gần $A$).$M$ là điểm đối xứng của $L$ qua $BC$ . Chứng minh đường tròn ngoại tiếp tam giác $BKM$ đi qua trung điểm của $BC$ .

 

Lời giải bài toán 78.

Bổ đề  Cho tam giác $ABC$ có tia phân giác trong $AD$. Trên đoạn thẳng $AD$ lấy các điểm $K,L$ ($K$ nằm giữa $A$ và $L$) thỏa mãn $\angle{ACK}=\angle{LCB}$. Chứng minh rằng $\angle{ABK}=\angle{LBC}$

 

(Bổ đề khá quen thuộc nên mình không chứng minh). 

Spoiler

Vẽ đường tròn $(ACK)$. $BK$ cắt đường tròn này tại điểm $H$. Chứng minh $\triangle{ABH}\sim \triangle{LBC}$.

 

Quay trở lại bài toán

Vẽ đường kính $PW$ của $(O)$. Gọi trung điểm của $BC$ là $N$. Bài toán cần chứng minh trở thành chứng minh tứ giác $BKNM$ nội tiếp. Dễ chứng minh được $N$ thuộc đường tròn đường kính $PC$.

Ta có: $\angle{ACL}=\angle{CLW}-\angle{LAC}=\angle{CLW}-\frac{\hat{A}}{2}$  $(1)$

Mặt khác $\angle{KCN}=\angle{KPN}=\angle{KPC}-\angle{WBC}$

Mà $\angle{WBC}=\frac{\hat{A}}{2}$ và $\angle{KPC}=\angle{CLW}$

$\Rightarrow \angle{KCN}=\angle{CLW}-\frac{\hat{A}}{2}$ $(2)$

Từ $(1)$ và $(2)$ suy ra $\angle{KCN}=\angle{ACL}$ $\Rightarrow \angle{ACK}=\angle{LCB}$

Áp dụng bổ đề thì ta có ngay $\angle{ABK}=\angle{LBC}$  $(3)$

                                              $\Rightarrow \angle{ABK}=\angle{NBM}$

                                              $\Rightarrow \angle{ABN}=\angle{KBM}$

Mà $\angle{ABN}=\angle{AWC}$ (cùng chắn $AC$)

Nên $\angle{AWC}=\angle{KBM}$  $(4)$

Từ $(3)$ ta cũng có $\angle{BKW}=\angle{ABK}+\frac{\hat{A}}{2}=\angle{LBC}+\angle{CBW}=\angle{LBW}$

$\Rightarrow \angle{BKW}=\angle{LBW}$

$\Rightarrow \triangle{BLW} \sim \triangle{KBW}$

$\Rightarrow \frac{BW}{BL}=\frac{KW}{BK}$

$\Rightarrow \frac{WC}{BM}=\frac{KW}{BK}$ $(BL=BM,BW=WC)$  

$\Rightarrow \frac{WC}{KW}=\frac{BM}{BK}$ $(5)$

Từ $(4)(5)$ suy ra $\triangle{BKM} \sim \triangle{WKC}$

                 $\Rightarrow \angle{BKM}=\angle{WKC}$

Mặt khác $\angle{WKC}=\angle{LNB}=\angle{BNM}$ (Vì tứ giác $BLNC$ nội tiếp và $M,L$ đối xứng qua $BC$)

Suy ra $ \angle{BKM}=\angle{BNM}$ hay tứ giác $BKNM$ nội tiếp tức là $(BKM)$ đi qua trung điểm $N$ của đoạn thẳng $BC$ (đpcm)

Spoiler

Mấy bài của bác Tăng khó v.

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 04-05-2017 - 19:48

[Minhnksc]

Bài 79:(Sưu tầm)

Cho tam giác ABC; lấy điểm P trong tam giác sao cho $\angle{APC}=\angle{APB}=\angle{BPC}$. Gọi giao điểm của BP và AC là D; của CP và AB là E. Chứng minh rằng $DE\leq \frac{1}{4}(AB+AC)$

 

P/s: Chưa ai giải bài $74$ nhỉ? 

mình đang nghi ngờ bài này có dính tới định lý 4 điểm nhưng bị tắc ở chỗ chứng minh $OD^2+MD^2=OK^2$

P/s:Lâu rồi chưa thấy ai đăng BĐT và cực trị hình học nhỉ

[Minhnksc]

Trước khi đề xuất bài toán tiếp theo tôi có một yêu cầu nho nhỏ không biết các bạn có hưởng ứng không: Khi đăng bài mới xin hãy đăng kèm hình theo nếu có thể.
 
Bài 74: (Nguyễn Minh Hà)
Cho tam giác $ABC$, với tâm ngoại tiếp $(O)$ và tâm nội tiếp $I$. $D$ là hình chiếu của $I$ lên $BC$. $M$ là trung điểm $BC$. $K$ là điểm đối xứng của $M$ qua $AI$. Chứng minh rằng: $KD \perp OI$. 

NGUYEN MINH HA.png

 

Lời giải bài 74:
Gọi $O'$ là điểm đối xứng với O qua AI(1) $\Rightarrow$ OK đối xứng với O'M qua AI $\Rightarrow OK=O'M$
Từ (1) ta cũng dễ dàng suy ra $AO'\perp BC$
Gọi giao điểm của AO' và BC là E. Đặt $AB=c; AC=b; BC=a; AO=R$
 Dễ dàng chứng minh $2AE.R=b.c$
Theo định lý 4 điểm; $đpcm \Leftrightarrow OK^2-OD^2=IK^2-ID^2\Leftrightarrow OK^2-OD^2=IM^2-ID^2\Leftrightarrow O'M^2-(OM^2+DM^2)=MD^2\Leftrightarrow (ME^2+O'E^2)-(MD^2+R^2-MC^2)=MD^2\Leftrightarrow ME^2+(AE-AO')^2=2MD^2-CM^2+R^2\Leftrightarrow ME^2+(AE-R)^2=2MD^2-CM^2+R^2\Leftrightarrow ME^2+AE^2+2AE.R=2MD^2-MC^2\Leftrightarrow AM^2+b.c=(BM-BD)^2-CM^2$(2)
Thay $CM=BM=\frac{a}{2}; BD=\frac{a+c-b}{2}$ vào (2) ta có
$AM^2=\frac{b^2}{2}+\frac{c^2}{2}-\frac{a^2}{4}$ (Luôn đúng theo công thức đường trung tuyến)

Spoiler

Bài của bác Tăng rất chi là chầy cối .

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 05-05-2017 - 16:58

[Nguyenphuctang]

$1$ số cách khác và ứng dụng của bài $74$ (của thầy Hùng)

    derakynay917new.pdf   311.78K   143 Số lần tải

[Uchiha sisui]

Xin đóng góp một bài tiếp theo cũng rất hay. Cố gắng được hơn 100 bài nào Topic     

 

Bài 80. (THTT T4/411) Cho tam giác ABC, M là điểm nằm trong tam giác. Gọi P, Q, R, H, G lần lượt là trọng tâm của các tam giác MBC, MAC, MAB, PQR, ABC. Chứng minh rằng ba điểm M, H, G thẳng hàng.

[NHoang1608]

Bài 80. (THTT T4/411) Cho tam giác ABC, M là điểm nằm trong tam giác. Gọi P, Q, R, H, G lần lượt là trọng tâm của các tam giác MBC, MAC, MAB, PQR, ABC. Chứng minh rằng ba điểm M, H, G thẳng hàng.

Lời giải bài toán 80.

 

Gọi trung điểm của $AB,BC,CA$ lần lượt là $E,F,J$. Dễ thấy các bộ điểm sau thẳng hàng:

\[(A,G,F); (B,G,J); (C,G,E); (M,P,F); (M,R,E); (M,Q,J)\]

Vì $G$ là trọng tâm tam giác $ABC$ nên hiển nhiên $G$ cũng là trọng tâm tam giác $EJF$.

Vẽ trung tuyến $JX$ và $QY$ của tam giác $EJF, RQP \Rightarrow$ 3 điểm $Q,H,Y$ và $J,G,X$ thẳng hàng.

Ta có: $\frac{MP}{MF}=\frac{MQ}{MJ}=\frac{MR}{ME}=\frac{2}{3}$

          $\Rightarrow \triangle{RQP}\sim \triangle{EJF}$ mà $QY,JX$ là các trung tuyến tương ứng suy ra: $\frac{QY}{JX}=\frac{2}{3}$

Mà $\frac{MQ}{MJ}=\frac{2}{3}$

Áp dụng định lí $Thales$ đảo ta có $X,Y,M$ thẳng hàng và $XJ//YQ$

Mặt khác $\frac{XG}{GJ}=\frac{YH}{HQ}=\frac{1}{2}$

Áp dụng định lí chùm đường thẳng đồng quy ta có $G,H,M$ thẳng hàng.

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 07-05-2017 - 21:06

[Minhnksc]

Bài 81(APMO):

Cho tam giác $ABC$; đường cao $AD;BE;CF$ và $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Chứng minh rằng $OA;OB;OC;OD;OE;OF$ chia tam giác $ABC$ thành $3$ cặp tam giác bằng nhau.

 

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 07-05-2017 - 21:43

[Uchiha sisui]

Tiếp với một bài nữa    ! ủng hộ Topic Thầy Hùng nào mọi người '' chém nhiệt tình'' nào !     

 

Bài 82. Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp tam giác ABC. M là điểm nằm trong tam  giác ABC sao cho $\widehat{BMC}=\widehat{BIC}$. Đường thẳng qua M song song với BC cắt AB, AC lần lượt tại P và Q. Các đường thẳng qua m song song với AB, AC cắt BC tại D và E

 

a) Chứng minh rằng bốn điểm M, Q, C, D đồng viên

 

b) Gọi N là giao điểm của PD và QE. Chứng minh rằng khi M thay đổi thì N luôn chạy trên một đường tròn cố định.

 

                                                                       (Trích đề thi thử chuyên KHTN-Hà Nội năm 2015 Lần 2 môn toán Chuyên)

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Uchiha sisui: 07-05-2017 - 22:51

[Uchiha sisui]

Tiếp với một bài nữa    ! ủng hộ Topic Thầy Hùng nào mọi người '' chém nhiệt tình'' nào !     

 

Bài 82. Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp tam giác ABC. M là điểm nằm trong tam  giác ABC sao cho $\widehat{BMC}=\widehat{BIC}$. Đường thẳng qua M song song với BC cắt AB, AC lần lượt tại P và Q. Các đường thẳng qua m song song với AB, AC cắt BC tại D và E

 

a) Chứng minh rằng bốn điểm M, Q, C, D đồng viên

 

b) Gọi N là giao điểm của PD và QE. Chứng minh rằng khi M thay đổi thì N luôn chạy trên một đường tròn cố định.

 

                                                                       (Trích đề thi thử chuyên KHTN-Hà Nội năm 2015 Lần 2 môn toán Chuyên)

Nhân tiện cho mình hỏi mọi người dùng Phần mềm gì vẽ hình vậy mình dùng geogra rồi cut ra paint nhưng hình nó bé quá

[Uchiha sisui]

Bài 81(APMO):

Cho tam giác $ABC$; đường cao $AD;BE;CF$ và $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Chứng minh rằng $OA;OB;OC;OD;OE;OF$ chia tam giác $ABC$ thành $3$ cặp tam giác bằng nhau.

geogebra-export (1).png

CUT HÌNH RA PANIT KIỂU J ĐỂ TO THẾ BẠN

[Nguyenphuctang]

Nhân tiện cho mình hỏi mọi người dùng Phần mềm gì vẽ hình vậy mình dùng geogra rồi cut ra paint nhưng hình nó bé quá

Bạn xài sketchpad (tải bản full c*rack , hình như bên mathscope có link full c*rack ). Sau khi vẽ hình (có thể điều chỉnh độ dày đường thẳng, màu sau cho đẹp là ok ). Vẽ xong hình Ctrl + A rồi bấm Ctrl +C vào paint dán ra (Ctrl + C) rồi lưu lại. Còn vế geogebra đừng nên cut ra paint vào chỗ xuất bản ảnh vào lưu lại thôi. 

CUT HÌNH RA PANIT KIỂU J ĐỂ TO THẾ BẠN

Bạn vào xuất dưới dạng hình png rồi chỉnh size thường thì để to thì 1:1,5 hoặc 1:2 tùy vào người chỉnh.

Bài toán đề xuất tiếp theo:

Bài 83: (Sưu tầm)

Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

 

 

Bài viết đã được chỉnh sửa nội dung bởi Nguyenphuctang: 08-05-2017 - 22:11

[Kiratran]

trùng rồi bạn ơi, cái này mình có đọc trong sách rồi, đề là chứng minh $M,H,P$ thẳng hàng ( $H$ là trực tâm $\triangle ABC$)

 

Bạn xài sketchpad (tải bản full c*rack , hình như bên mathscope có link full c*rack ). Sau khi vẽ hình (có thể điều chỉnh độ dày đường thẳng, màu sau cho đẹp là ok ). Vẽ xong hình Ctrl + A rồi bấm Ctrl +C vào paint dán ra (Ctrl + C) rồi lưu lại. Còn vế geogebra đừng nên cut ra paint vào chỗ xuất bản ảnh vào lưu lại thôi. 

Bạn vào xuất dưới dạng hình png rồi chỉnh size thường thì để to thì 1:1,5 hoặc 1:2 tùy vào người chỉnh.

Bài toán đề xuất tiếp theo:

Bài 83: (Tăng)

Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Đây là $1$ tính chất mình thấy được khi làm $1$ bài không biết bài này có trùng với bài nào không nữa, nếu trùng xin hãy nhắn tin để tôi sửa lại nguồn.
 

83.png

Bài viết đã được chỉnh sửa nội dung bởi Kiratran: 08-05-2017 - 19:26

[Uchiha sisui]

Bạn xài sketchpad (tải bản full c*rack , hình như bên mathscope có link full c*rack ). Sau khi vẽ hình (có thể điều chỉnh độ dày đường thẳng, màu sau cho đẹp là ok ). Vẽ xong hình Ctrl + A rồi bấm Ctrl +C vào paint dán ra (Ctrl + C) rồi lưu lại. Còn vế geogebra đừng nên cut ra paint vào chỗ xuất bản ảnh vào lưu lại thôi. 

Bạn vào xuất dưới dạng hình png rồi chỉnh size thường thì để to thì 1:1,5 hoặc 1:2 tùy vào người chỉnh.

Bài toán đề xuất tiếp theo:

Bài 83: (Tăng)

Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Đây là $1$ tính chất mình thấy được khi làm $1$ bài không biết bài này có trùng với bài nào không nữa, nếu trùng xin hãy nhắn tin để tôi sửa lại nguồn.
 

83.png

Cấu hình bài này giống IMO 2014

[HoangKhanh2002]

Bài 81(APMO):

Cho tam giác $ABC$; đường cao $AD;BE;CF$ và $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Chứng minh rằng $OA;OB;OC;OD;OE;OF$ chia tam giác $ABC$ thành $3$ cặp tam giác bằng nhau.

geogebra-export (1).png

$\boxed{\text{Lời giải bài 81}}$

Gọi P, Q lần lượt là trung điểm của BC, AC

Dễ thấy: $\widehat{BOF}=\frac{1}{2}\widehat{BOC}=\widehat{BAC}$

Lại có: $\widehat{BPO}=\widehat{BEA}=90^o \Rightarrow \Delta BOP \sim \Delta BAE (g.g)\Rightarrow \frac{OP}{EA}=\frac{OB}{BA}$

Chứng minh tương tự: $\Delta BDA \sim \Delta OQA(g.g)\Rightarrow \frac{BD}{OQ}=\frac{BA}{OA}$

Từ hai điều trên ta có: $\frac{OP}{EA}=\frac{OQ}{BD}\Rightarrow OP.BD=EA.OQ\Rightarrow S_{OBD}=S_{OAE}$

Các cặp còn lại chứng minh tương tự

[Uchiha sisui]

Xin đề xuất bài toán tiếp theo!   

 

Bài 84. ( Sưu tầm) Cho hai đường tròn (O) và (O') tiếp xúc trong tại K , ( (O') nằm trong (O) ) . Điểm A nằm trên (O) sao cho A, O, O' không thẳng hàng. Các tiếp tuyến AD, AE của (O') cắt đường tròn (O) lần lượt tại các điểm thứ hai là B và C (D, E là các tiếp điểm). Đường thẳng AO' cắt (O) tại điểm thứ hai là F. Chứng minh rằng BC, DE, FK đồng quy.

 

 

 

 

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Uchiha sisui: 08-05-2017 - 20:29

[Mr Cooper]

Bài 83: (Sưu tầm)

Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Lời giải bài toán 83.

Bổ đề: Cho tam giác $MNP$.$H$ là trung điểm của $BC$.$N_1,P_1$ lần lượt là chân đường vuông góc hạ từ $N,P$. Chứng minh rằng $(HNP_1),(HPN_1)$ và $MH$ đồng quy

Chứng minh. Giả sử $K_1,K_2$ lần lượt là giao điểm của MH với $(HNP_1),(HPN_1)$

Theo tính chất cát tuyến: $MP_1.MN=MK_1.MH;MN_1.MP=MK_2.MH$

$MP_1.MN=MN_1.MP$ $\Rightarrow MK_1.MH=MK_2.MH$ $\Rightarrow MK_1=MK_2$ $\Rightarrow K_1 \equiv K_2$

$\Rightarrow$ $(HNP_1),(HPN_1)$ và $MH$ đồng quy 

Quay trở lại bài toán.

Gọi $I$ là giao điểm của $BC$ và $B_1C_1$ 

Từ bổ đề trên ta có được $A,P,O$ thẳng hàng

$\angle CB_1P= \angle BOP = \angle AC_1P$ $\Rightarrow$ $A,B_1,P,C_1$ cùng nằm trên $1$ đường tròn

Lại có $A,B_1,M,C_1$ nằm trên đường tròn đường kính $AM$ 

$\Rightarrow A,B_1,M,P,C_1$ cùng nằm trên đường tròn đường kính $AM$ 

$\Rightarrow \angle APM =90^{\circ}$ $\Rightarrow MP \perp OA$ $(1)$

Theo định Lý $\text{Brocard}$ ta có: $O$ là trực tâm của tam giác $AMI$ $\Rightarrow IM \perp OA$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow I,M,P$ thẳng hàng

Vậy Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 09-05-2017 - 17:41

[Mr Cooper]

Bài Toán 85.(Sưu tầm) Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ tiếp xúc với $AB,AC$ lần lượt tại $M,N$ và tiếp xúc với $(O)$ tại $J$.Chứng minh rằng $JN$ đi qua điểm chính giữa cung $AC$

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 10-05-2017 - 11:05

[IHateMath]

Lời giải bài toán 83.

...Theo định Lý $\text{Brocard}$ ta có: $O$ là trực tâm của tam giác $AMI$ $\Rightarrow IM \perp OA$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow I,M,P$ thẳng hàng

Vậy Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Chỗ này dùng Brocard hơi quá tay, hơn nữa Brocard không được học ở chương trình toán THCS! (chứng minh định lý này cũng không đơn giản) Để giải quyết chỗ này ta nên dùng ý tưởng trục đẳng phương thì hay hơn (mình biết là khái niệm này không được học, nhưng về ý tưởng thì đơn giản và sáng sủa hơn rất nhiều!).