Đến nội dung

01634908884

01634908884

Đăng ký: 29-07-2015
Offline Đăng nhập: 04-03-2019 - 07:31
***--

#715513 $\sum_{1}^{n}\frac{u_{k}...

Gửi bởi 01634908884 trong 13-09-2018 - 21:12

Rất tiếc là không 😁


#715484 $\sum_{1}^{n}\frac{u_{k}...

Gửi bởi 01634908884 trong 12-09-2018 - 22:44

Cho $u_{1} =1,u_{n+1}=u_{n}^{2019}+u_{n}$
Tìm lim $\sum_{1}^{n}\frac{u_{k}}{u_{k+1}}$


#713406 $f: R^+ \to R^+; f(f(x)+x^2+2y)=f(x)+x^2+2f(y) $

Gửi bởi 01634908884 trong 28-07-2018 - 17:11

Thay $f(x)$ bởi $y^{2}$ và y bởi xy ta có:
$f((x+y)^{2})=(x+y)^{2}+2f(xy)-2xy$ (1)
Thay y=1 vào (1):
$f((x+1)^{2})=(x+1)^{2}-2x+2f(x)$ (2)
Hay: $4(f(x)-x)=2[f((x+1)^{2})-(x+1)^{2}]$
Thay $(x+1)^{2}$ bởi x vào (2) có:
$2[f((x+1)^{2})-(x+1)^{2}]=f(x)-x$
Dẫn đến: $4(f(x)-x)=f(x)-x$
Suy ra $f(x)=x$

Để được
Thay $(x+1)^{2}$ bởi x vào (2) có:
$2[f((x+1)^{2})-(x+1)^{2}]=f(x)-x$ hóa ra (x+1) ^2=x à


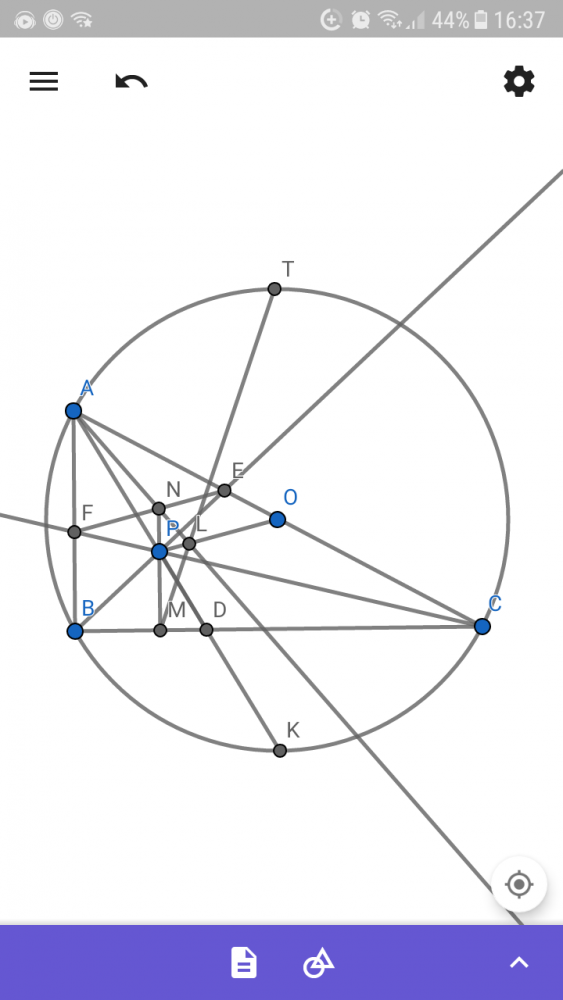
#710992 ML luôn đi qua điểm chính giữa cung BAC

Gửi bởi 01634908884 trong 15-06-2018 - 16:31

Tam giác ABC nội tiếp (O) ,phân giác AD, D thuộc BC,P là một điển bất kì thuộc AD,BP cắt AC tại E , CP cắt AB tại F, M là hình chiếu của P lên BC, MP cắt EF tại N , AN cắt OP tại L. Chứng minh ML luôn đi qua điểm chính giữa cung BAC

File gửi kèm




#710882 $f: R^+ \to R^+; f(f(x)+x^2+2y)=f(x)+x^2+2f(y) $

Gửi bởi 01634908884 trong 14-06-2018 - 15:36

Tìm hàm số f thỏa mãn $f: R^+ \to R^+; f(f(x)+x^2+2y)=f(x)+x^2+2f(y) $. với x, y>0, x, y là số thực


#709796 Đường thẳng ST đi qua G

Gửi bởi 01634908884 trong 02-06-2018 - 21:40

Tam giác ABC nhọn nội tiếp (O). Xét M, N lần lượt di chuyển trên AB, AC và (AMN) cắt (O) tại S khác A.Gọi T là điểm đối xứng với S qua MN.Đường cao AD cắt (O ) tại G. Chứng minh rằng nếu T thuộc BC khi M, N chuyển động thì ST đi qua G

File gửi kèm




#709689 K là tâm nội tiếp tam giác AXY

Gửi bởi 01634908884 trong 31-05-2018 - 21:49

Tam giác ABC, tâm nội tiếp (I), tâm ngoại tiếp (O) , trưc tâm H, (I) tiếp xúc AC, AB tại E,F. Lấy K đối xứng I qua EF. Đường cao BX, CY. Chứng minh K là tâm nội tiếp tam giác AXY


#701582 $\widehat{AFL}=\widehat{BAC}$

Gửi bởi 01634908884 trong 12-02-2018 - 23:06

Cho tam giác ABC cân tại A, đường cao AH. Đường tròn (O) đi qua A, B cắt đoạn AH tại K. Điểm L thuộc đoạn AB sao cho KL song song AC. Gọi E = BK ∩CL. Đường thẳng AE cắt lại (O) tại điểm thứ hai F. Chứng minh rằng $\widehat{AFL}=\widehat{BAC}$


#698849 Tồn tại một điểm có thể vẽ vô số đường thẳng tốt

Gửi bởi 01634908884 trong 24-12-2017 - 21:23

Giả sử có $n$ điểm trong mặt phẳng sao cho chúng không có ba điểm thẳng hàng. Ta gọi $l$ là đường thẳng tốt nếu $l$ có thể chia $n$ điểm vào hai tập $A,B$ sao cho tổng khoảng cách từ các điểm thuộc $A$ đến $l$ bằng tổng khoảng cách từ các điểm thuộc $B$ đến $l.$ Chứng minh tồn tại một điểm thuộc mặt phẳng mà qua đó có thể kẻ vô số đường thẳng tốt.




#685450 AN vuông góc với BD

Gửi bởi 01634908884 trong 24-06-2017 - 09:39

$M$ là trung điểm $AB$ rồi thì sao $I$ là trung điểm $AB$ được


Mình nhầm đề
  • NHN yêu thích


#667139 Tìm giá trị lớn nhất $P=xy+2yz+5zx$

Gửi bởi 01634908884 trong 05-01-2017 - 19:50

Cho $x.y.z$ dương thỏa mãn $x^{2}+y^{2}+z^{2}+1= 2(xy+yz+xz)$.Tìm giá trị lớn nhất $P=xy+2yz+5zx$




#666900 $\sum \frac{a^{4}}{(b+c)(b^{2...

Gửi bởi 01634908884 trong 04-01-2017 - 10:49

Cho a,b,c dương $a+b+c=3$

CMR$\sum \frac{a^{4}}{(b+c)(b^{2}+c^{2})}\geq \frac{3}{4}$




#660696 $\sum \frac{a}{bc+1}\geq 1$

Gửi bởi 01634908884 trong 05-11-2016 - 19:31

2 số=0; 1 số =1




#648420 $\frac{a+\sqrt{ab}+\sqrt[3]{abc}...

Gửi bởi 01634908884 trong 07-08-2016 - 15:54

Cho a,b,c thực dương.CM

a,$\frac{a+\sqrt{ab}+\sqrt[3]{abc}}{3}\leq \sqrt[3]{a.\frac{a+b}{2}.\frac{a+b+c}{3}}$

b,$\frac{a+\sqrt{ab}+\sqrt[3]{abc}}{3}\leq \frac{a+b+c}{3}$




#636161 $(a+\frac{1}{a^{2}})+(b^{2}...

Gửi bởi 01634908884 trong 28-05-2016 - 09:04

Cho $a,b$ dương

thỏa mãn $ab+1\leq b$

cmr $(a+\frac{1}{a^{2}})+(b^{2}+\frac{1}{b})\geq 9$






  1. Diễn đàn Toán học
  2. → Đang xem trang cá nhân: Likes: 01634908884