Tỉnh e mấy anh làm đc 5 bài trên tổng số 7 bài

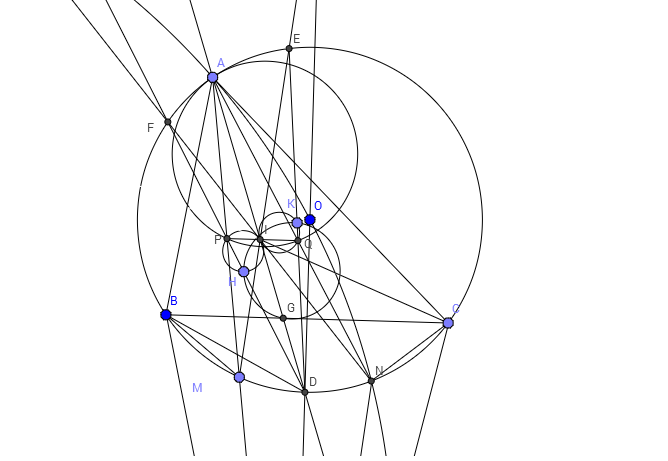
Lời giải câu hình:

Câu a): Dễ chứng minh

Câu b)

Sử dụng định lý Pascal chứng minh được $P,I,Q$ thẳng hàng. (1)

Xét phép nghịch đảo tâm D phương tích $DI^2$ biến $H$ thành $P$, biến $K$ thành $Q$ và biến $G$ thành $A$, do đó ta sẽ đi chứng minh $(APQ)$ tiếp xúc $(O)$.

Mặt khác $\widehat{IAQ}=\widehat{IEQ}$ nên tứ giác $AEQI$ nội tiếp.

Suy ra $\widehat{AQI}=\widehat{AEI}=\widehat{ACM}$   (2)

Từ (1) và (2) suy ra đường tròn $(APQ)$ tiếp xúc với $(O)$.

Từ đó suy ra ĐPCM.

P/s: Vẽ hình hơi tệ

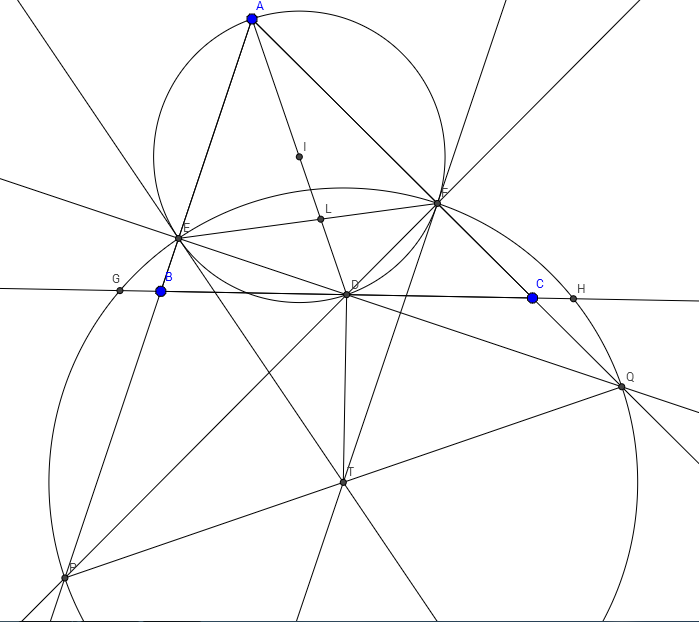
Em xin giải nốt câu hình b (em giải ở nhà thầy khi chiều, k biết câu hình có trùng lời giải giống trong link thầy Hùng k )

Câu hình b:

Đường đối cực của $T$ đi qua $L$ nên đường đối cực của $L$ đi qua $T$ hay $P,T,Q$ thẳng hàng.

Từ đó suy ra $PEFQ$ là tứ giác nội tiếp đường tròn tâm $T$.

$DB=DC$ nên đường thẳng $BC$ cắt $(T)$ tại $G$ và $H$ thì $DG=DH$ (theo định lý con bướm).

Nên $TD\perp BC$

Vậy $T$ thuộc đường trung trực của cạnh $BC$.

Câu 2a:

Ban đầu chứng minh dãy bị chặn trên bởi $1$.

Tiếp theo chứng minh nó là dãy tăng và kể từ $n=6$ trở đi thì $a_n\geq \frac{1}{2}$

Câu hình b) có lẽ là đề Nga đã lâu rồi và mình đã viết bài tổng quát ở đây http://analgeomatica...-tren-thtt.html

 

Link gốc http://www.artofprob...ommunity/h16779

Câu a hạ AH là đường cao tam giác ABC thì AH là đường đẳng giác của tam giác ABC với cạnh AM

Ta có: $\widehat{DAM}=\widehat{DAC}-\widehat{OAC}$

$\widehat{MND}=\widehat{HAF}-\widehat{EAD}$

Từ đó dẫn đến $\widehat{DAM}=\widehat{DAM}$ nên tứ giác $AMDN$ nội tiếp.

Suy ra điểm cố định đó là $D$

Bạn có thể chứng minh lại , vừa với sức THCS được không ?

Kiến thức THCS có thể chứng minh được, lời giải đầu tiên trong này là một ví dụ (mặc dù có sử dụng trục đẳng phương hơi vượt kiến thức THCS một tí)

http://diendantoanho...ịnh-lí-brocard/

Cho tứ giác ABCD nội tiếp đường tròn tâm O . Gọi M,N,P lần lượt là giao điểm của AB với CD,AD với BC ,AC với BD.

Chứng minh rằng : $OP\perp MN$

Đây chính là hệ quả của định lý Brocard 

$S=\frac{1}{(x-1)x-1}$ không phải $S=(x-1)x-1$ nên tất nhiên nếu $x$ cực kì lớn thì $S\rightarrow 0$

$S_{n+1}\sqrt{5}=\frac{a^{n+1}}{x^{n+1}(a-x)}-\frac{b^{n+1}}{x^{n+1}(b-x)}+\frac{b}{x(b-x)}-\frac{a}{x(a-x)}$

$=\frac{a^{n+1}}{x^{n+1}(a-x)}-\frac{b^{n+1}}{x^{n+1}(b-x)}+\frac{\sqrt{5}}{x^2-x-1}$

Chỉ cần chứng minh:

$lim(\frac{a^{n+1}}{x^{n+1}(a-x)}-\frac{b^{n+1}}{x^{n+1}(b-x)})=0$

Phần này đơn giản, vì $|a|<x$ và $|b|< x$ nên dễ dàng suy ra điều phải chứng minh.

Vậy $limS=\frac{1}{x^2-x-1}$

Cho dãy $Fibonaci$ với $U_{1}=0;U_{2}=1;U_{n+2}=U_{n+1}+U{n}$

Chứng minh $S=\sum_{i=1}^{n}\frac{U_{i}}{x^i} = (x-1)x-1$

Với n tiến đến vô cùng,$x \geq 2$, $x$ là số tự nhiên.

Đặc biệt,với $x=2;3;8;10;...$,ta có $S$ lần lượt bằng$U_{3};U_{6};U_{11};U_{12};...$

Dãy Fibonacci thì có $U_1=1$ chứ sao lại bằng $0$ 

Chẳng thấy nó đặc biệt chỗ nào cả

Ta đặt $S_{n+1}=\sum_{i=1}^{n+1}\frac{U_i}{x_i}$

Khi đó: $S_{n+1}-S_n=\frac{U_{n+1}}{x^{n+1}} $

Chứng minh được: $U_{n+1}=\frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^n$

Đặt $a=\frac{1+\sqrt{5}}{2}$ và $b=\frac{1-\sqrt{5}}{2}$

Khi đó $(S_{n+1}-S_n)\sqrt{5}=\frac{a^n-b^n}{x^{n+1}}$

$<=>S_{n+1}\sqrt{5}-\frac{a^{n+1}}{x^{n+1}(a-x)}+\frac{b^{n+1}}{x^{n+1}(b-x)}$

$=S_n\sqrt{5}-\frac{a^n}{x^n(a-x)}+\frac{b^n}{x^n(b-x)}=...=S_1\sqrt{5}-\frac{a}{x(a-x)}+\frac{b}{x(b-x)}=\frac{b}{x(b-x)}-\frac{a}{x(a-x)}$

Do đó: 

$S_{n+1}\sqrt{5}=\frac{a^{n+1}}{x^{n+1}(a-x)}-\frac{b^{n+1}}{x^{n+1}(b-x)}+\frac{b}{x(b-x)}-\frac{a}{x(a-x)}$

$=\frac{a^{n+1}}{x^{n+1}(a-x)}-\frac{b^{n+1}}{x^{n+1}(b-x)}+\frac{\sqrt{5}}{x^2-x-1}$

Bài này mình nghĩ ra được 5 cách:

Cách 1: Dùng vecto như Mai Quoc Tuan

Cách 2: Vẽ AK vuông góc AB

Cách 3: Dùng định lý 4 điểm

Cách 4: Lấy trung điểm K của FB rồi chứng minh G là trực tâm tam giác ECK

Cách 5: Dùng tọa độ 

Áp dụng BĐT Holder, ta có: $(1+a)^{3}\leq (1+1)(1+\frac{a\sqrt{a}}{b\sqrt{b}})(1+ab\sqrt{ab})$

Suy ra: $\frac{1}{(1+a)^{3}}\geq \frac{b\sqrt{b}}{2(a\sqrt{a}+a\sqrt{b})(1+ab\sqrt{ab})}$

Tương tự, suy ra: $\frac{1}{(1+b)^{3}}\geq \frac{a\sqrt{a}}{2(a\sqrt{a}+a\sqrt{b})(1+ab\sqrt{ab})}$

Cộng lại ta có: $\frac{1}{(1+a)^{3}}+\frac{1}{(1+b)^{3}}\geq \frac{1}{2(1+ab\sqrt{ab})}$
Thiết lập BĐT tương tự với $c$ và $d$, cộng lại ta có:
$VT\geq \frac{1}{2(1+ab\sqrt{ab})}+\frac{1}{2(1+cd\sqrt{cd})}=\frac{1}{2(1+ab\sqrt{ab})}+\frac{ab\sqrt{ab}}{2(ab\sqrt{ab}+1)}=\frac{1}{2}$

Đẳng thức xảy ra khi và chỉ khi $a=b=c=d=1$

Kinh khủng quá

Sử dụng BĐT Holder ta có:

$4(\sum \frac{1}{(1+a)^3})^2\geq (\sum \frac{1}{(1+a)^2})^3$

Lại có: $\frac{1}{(1+a)^2}+\frac{1}{(1+b)^2}\geq \frac{1}{(a+b)(a+\frac{1}{b})}+\frac{1}{(a+b)(b+\frac{1}{a})}=\frac{1}{ab+1}=\frac{1}{1+\frac{1}{cd}}=\frac{cd}{1+cd}$

Tương tự: $\frac{1}{(1+c)^2}+\frac{1}{(1+d)^2}\geq \frac{1}{1+cd}$

Từ đó suy ra ĐPCM

 

 

Câu bất quen quá.

Không mất tính tổng quát giả sử $c=min(a,b,c)$

Đặt $a=c+x,b=c+y \left(x,y\geq0\right)$

Theo giả thiết ta có: $max\left \{ a;b;c \right \}-min\left \{ a;b;c \right \}\leq 1$ nên suy ra $0\leq x,y \leq 1$

Ta có: $1+a^3+b^3+c^3+6abc\geq 3a^2b+3b^2c+3c^2a$

$\Leftrightarrow 1+ \left(c+x\right)^3+\left(c+y\right)^3+c^3+6c\left(c+x\right)\left(c+y\right) \geq 3\left(c+x\right)^2\left(c+y\right)+3c\left(c+y\right)^2+3c^2\left(c+x\right)$

$\Leftrightarrow \left(2x^3+y^3-3x^2y\right)+\left(1-x^3\right) \geq 0$

Áp dụng bất đẳng thức $AM-GM$ ta lại có: $2x^3+y^3=x^3+x^3+y^3\geq 3x^2y$

Lại có: $x\leq 1 \Rightarrow 1-x^3\geq 0$

Vậy ta có điều phải chứng minh

 

Giả sử $b=min(a,b,c).$

Từ giả thiết bài toán suy ra được $(c-b)^3\leq 1$

Do đó chỉ cần chứng minh: $(c-b)^3+a^3+b^3+c^3+6abc\geq 3a^2b+3b^2c+3c^2a$

$<=>(a-c)^2(a+2c-3b)\geq 0$

Dễ thấy BĐT này luôn đúng

=> ĐPCM 

Kiến thức THCS thì sao ạ ?

Phép vị tự cũng có thể coi là kiến thức trung học sơ sở mà, không tin mở sách Nâng cao phát triển toán 9 của Vũ Hữu Bình vẫn có phép vị tự đấy thôi, nhưng là phát biểu theo một cách khác  

Cho $\triangle{ABC}$. 1 đường tròn tâm $O$ nội tiếp $\triangle$ tiếp xúc $BC$ tại $D$ . Đường tròn tâm $I$ là đường tròn bàng tiếp góc $A$  và tiếp xúc $BC$ tại $F$. Vẽ đường kính $DE$ của $(O)$. Chứng minh $A,E,F$ thẳng hàng

Xét phép vị tự tâm A tỉ số $\frac{R}{R_a}$ biến điểm $O$ thành điểm $I$ và biến điểm $E$ thành điểm $F$ nên $A,E,F$ thẳng hàng.

Có một bổ đề rất hay được ứng dụng và chứng minh nó bằng chính bài toán này là:

Cho tam giác $ABC$, $(O)$ là đường tròn nội tiếp tam giác, $O$ tiếp xúc với $BC$ tại $D$. Lấy điểm $F$ thuộc BC sao cho $BD=CF$. Vẽ đường kính $DE$ của $O$ thì khi đó $A,E,F$ thẳng hàng.

Có tất cả 2n đội bóng, thì mỗi đội sẽ đá với (2n - 1) đội còn lại. Có tất cả C(2n,2) = n.(2n - 1)  trận đấu.

Như vậy, trong mỗi vòng đấu (từ vòng 1, 2, ..., 2n -1 ) ta luôn tổ chức n trận đấu cho từng cặp (chưa gặp nhau) trong 2n đội bóng thì sẽ luôn thỏa mãn được ycbt. 

Muốn cụ thể hơn bạn có thể ký hiệu số đội bóng và số vòng đấu, rồi lập một quy tắc nào đó cho 2 đội sẽ gặp nhau trong vòng i (lưu ý là có rất nhiều cách để ta bắt cặp).

chọn 2 đội trong 2n đội ta có 1 trận : $C_{2n}^{2}= \frac{(2n-1)2n}{2}$

mà 1 vòng có n trận diễn ra : $\frac{C_{2n}^{2}}{n}$

suy ra số trận là 2n-1

2 lời giải đều ấn tượng, lời giải của Minh hay đấy

Mấu chốt là bắt lịch đấu ra sao ấy ạ, chớ tính cái đó thì dễ rồi

làm kỹ ra đi. mình thấy làm gì có triệt tiêu :3 

$\frac{1}{^{\sqrt{1}}+\sqrt{2}}+ \frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{5}+\sqrt{6}}+.....+\frac{1}{\sqrt{223}+\sqrt{224}}$

$= \sqrt{2}-1+\sqrt{3}-\sqrt{2}+.....+\sqrt{224}-\sqrt{223}$

Sau khi triệt tiêu ta được: $= \sqrt{224}-1> 7$

Làm thế này:

Ta có: $2(\frac{1}{\sqrt{1}+\sqrt{2}}+...+\frac{1}{\sqrt{223}+\sqrt{224}})$

$>\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{224}+\sqrt{225}}=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{225}-\sqrt{224}=14$

Từ đó suy ra ĐPCM

              SỞ GIÁO DỤC VÀ ĐÀO TẠO                                                              ĐỀ THI HỌC KÌ I

     TRƯỜNG THPT CHUYÊN LƯƠNG VĂN TỤY                                          Năm học 2015-2016

                                                                                                                Môn Toán-Lớp 10 Chuyên

 

 

 

 

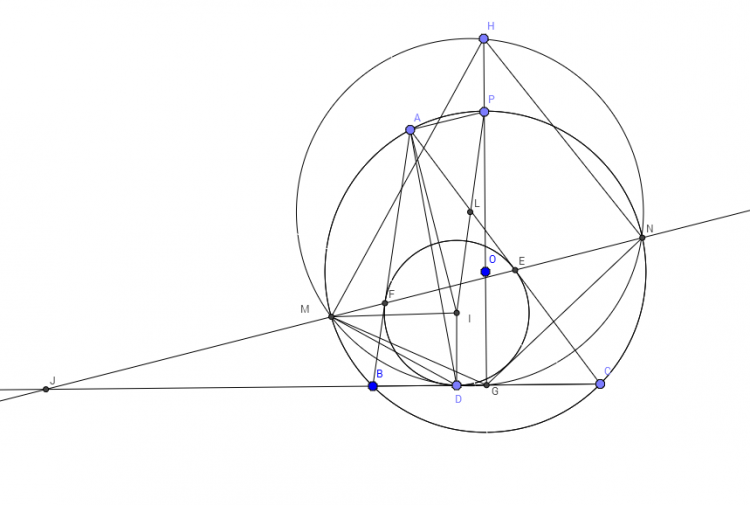
Câu 2 (3 điểm).Cho tam giác ABC nhọn,không cân nội tiếp đường tròn (O;R),ngoại tiếp đường tròn (I,r).G là trung điểm đoạn BC.Đường tròn (I;r) tiếp xúc với BC,CA,AB lần lượt tại D,E,F.Đường thẳng EF cắt đường tròn (O) tại M,N.Trên tia đối của tia OG lấy điểm H sao cho OH=R+r

 

a)Chứng minh M,N,D,G cùng nằm trên đường tròn tâm K

 

b)Chứng minh rằng K,D,H thẳng hàng

 

 

 

a) Kéo dài $MN$ cắt $BC$ tại $J$. Dễ chứng minh $(JDBC)=-1$, từ đó kết hợp với hệ thức Maclaurin suy ra $JD.JG=JM.JN$ 

=> ĐPCM

b) $OH$ cắt $(O)$ tại $P$ suy ra $PH=ID$, mà $PH//ID$ nên $PHID$ là hình bình hành.

Suy ra trung điểm $L$ của $DH$ cũng là trung điểm $L$ của $PI$.

Mặt khác dễ chứng minh góc $IAP$ vuông (dựa vào tính chất $AI$ cắt $(O)$ tại điểm chính giữa cung $BC$) nên dễ suy ra $APNM$ là hình thang cân.

$L$ thuộc trung trực của $AP$ nên $L$ cũng thuộc đường trung trực của $MN$.

Mà $L$ cũng là đường trung trực của $DG$ (dễ chứng minh).

Do đó $L\equiv K$ hay $K,D,H$ thằng hàng (đpcm)

Cho $a,b,c\geq 0$ thỏa mãn $ab+bc+ca=3$. Chứng minh rằng

$\frac{a}{2a^2+bc}+\frac{b}{2b^2+ac}+\frac{c}{2c^2+ab}\geq abc$

Ta có:

$\sum \frac{a}{2a^2+bc}\geq \frac{9}{2\sum a+\sum \frac{bc}{a}}=\frac{9abc}{2abc\sum a+\sum b^2c^2}=\frac{9abc}{(ab+bc+ca)^2}=abc$

 

                                                         DIỄN ĐÀN TOÁN HỌC VMF

                            ĐỀ THI MẪU KÌ THI HỌC SINH GIỎI QUỐC GIA MÔN TOÁN 2016

                                                                        ( Ngày 1 )

BÀi 1 : Tìm $a$ lớn nhất sao cho $3^m \geq  m^3+a, \forall m \in N, m \geq 4$

 

BÀI 2 : Tam giác ABC với tâm đường tròn nội tiếp $I$. Khi đó 4 đường thẳng Euler của các tam giác BIC, CIA, AIB, ABC đồng quy tại 1 điểm

BÀi 3 : a. Cho tam giác ABC. Trên các đường thẳng AB, BC, CA lấy các điểm P, Q, R tương ứng. Chứng minh rằng các đường tròn ngoại tiếp của tam giác APR, BPQ, CQR đồng quy tại một điểm.

b. Cho 4 đường tròn $S_1 ,S_2 ,S_3 ,S_4$ . Giả sử $S_1, S_2$ cắt nhau tại $A_1 , A_2$ ; $S_2 ,S_3$ cắt nhau tại $B_1 ,B_2$ ; $S_3 ,S_4$ cắt nhau tại $C_1 ,C_2$ ; $S_4 ,S_1$ cắt nhau $D_1 ,D_2$ . Chứng minh rằng nếu các điểm $A_1 , B_1 ,C_1 ,D_1$ nằm trên 1 đường tròn S ( hoặc đường thẳng) thì các điểm $A_2 ,B_2 ,C_2 ,D_2$ cũng nằm trên 1 đường tròn ( hoặc đường thẳng).

BÀI 4 : Một dãy có $2015$ phòng, ban đầu trong mỗi phòng có 1 người. Sau mỗi ngày có 2 người nào đó chuyển sang phòng kề với phòng mình đang ở nhưng theo $2$ chiều ngược nhau. Hỏi :

 a/ Liệu có một ngày nào đó không có người nào ở trong phòng chẵn hay không?

 b/ Liệu có một ngày nào đó có $1008$ người ở phòng $2015$ được không?

 

Câu 3a chẳng phải là định lý Miquel ạ

-------------------------------------------

@ducvipdh12: thực chất anh thêm câu a cho vui )

Bạn ơi cho tôi hỏi
Dòng thứ 4 bạn đã tìm được công thức truy hồi rồi, tôi dùng máy tính lập quy trình tính u15 thì kq không giống của bạn?

Đó công thức truy hồi khi $n\geq 2$ thôi bạn ạ, không tin bạn tính $u_2$ ra bằng công thức ở giả thiết rồi ráp vào công thức truy hồi thì sẽ không khớp

Không biết giải ri có đúng không nữa! :v

Em nghĩ lời giải ổn rồi ạ, nhưng một vài chỗ hơi tắt, ví dụ như chỗ có $ABCD$ là tứ giác điều hòa nên suy ra $AC$ là phân giác của góc $BLD$ cần phải nói rõ ra nữa

Cho dãy số $u_{n}$ được xác định bởi công thức $\left\{\begin{matrix} u_{1}=1 & & & & & & \\ u_{n}=u_{n-1}+u_{n-2}+...+u_{1}+(n-1)^2 & & & & & & \end{matrix}\right.$

Tính $u_{15}$

Ta xét với trường hợp $n\geq 2$

Ta có:$u_n=u_{n-1}+...+(n-1)^2$

$u_{n-1}=u_{n-2}+...+u_1+(n-2)^2$

Do đó: $u_n-u_{n-1}=u_{n-1}+2n-3<=>u_n=2u_{n-1}+2n-3$

$<=>u_n+2n+1=2(u_{n-1}+2(n-1)+1)$

Đặt $v_n=u_n+2n+1$ thì $v_2=u_2+2.2+1=7$ ta có:

$v_n=2v_{n-1}=2^{n-2}.v_2=7.2^{n-2}$

Nên $v_{15}=7.2^{13}=>u_{15}=7.2^{13}-2.15-1=57313$

Cho tứ giác ABCD nội tiếp. Gọi L, N lần lượt là trung điểm của AC, BD. Chứng minh BD là phân giác của góc ANC khi và chỉ khi AC là phân giác của góc BLD.

Gọi $G$ là giao điểm của $AC$ và $EF$, $K$ là giao điểm của $BD$ và $EF$.

$EF$ là đường đối cực của $H$, mà $G\in EF$ nên $G,H$ liên hợp đối với $(O)$ hay $(GHAC)=-1$

$NH$ là phân giác góc $ANC$ nên $NH\perp NG$ suy ra $O,N,G$ thẳng hàng.

Xét phép nghịch đảo tâm $O$ tỉ số $\overline{ON}.\overline{OG}$ biến điểm $L$ thành $K$ hay $O,L,K$ thẳng hàng.

$K\in EF$ là đường đối cực của $H$ nên $K,H$ liên hợp đối với $(O)$ hay $(KHDB)=-1$ mà $LH\perp LK$ nên $LH$ chính là đường phân giác của góc $DLB$ 

Phần còn lại chứng minh tương tự 

Bài này có thể giải đơn giản bằng vecto như sau:

Ta có: $\overrightarrow{AO}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$

Lại có: $\overrightarrow{IO}=\frac{1}{2}(\overrightarrow{IM}+\overrightarrow{IB})=\frac{1}{2}(\overrightarrow{IK}+\overrightarrow{KB}+\overrightarrow{KM}+\overrightarrow{IK})$

$=\overrightarrow{IK}+\frac{1}{2}(\overrightarrow{KH}+\overrightarrow{HM}-\frac{3}{4}\overrightarrow{BC})=\overrightarrow{IK}+\frac{1}{2}(\overrightarrow{CB}+\frac{1}{2}\overrightarrow{AB})$

Do đó: $\overrightarrow{AO}.\overrightarrow{IO}=(\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC})(\overrightarrow{IK}+\frac{1}{2}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{AB})$

Ngang đây có thể dùng công thức tính bán kính đường tròn ngoại tiếp tam giác là ra. (cách này khỏi nghĩ )

Mình xin đề ra kỳ này của toán học tuổi trẻ ạ, vì mua không kịp mà giờ đang cần ạ!

Chụp giúp mình lại 1 tấm hình là được rồi ạ!

Mình cám ơn nhiều!

Còn 1 câu hình nữa là: 

Cho tam giác ABC với (O). H theo thứ tự là đường tròn ngoại tiếp và trực tâm tam giác. P là điểm bất kì trên OH. A0; B0; C0 theo thứ tự là giao điểm của AH;BH;CH và BC;CA;CA. A1;B1;C1 theo thứ tự là giao điểm thứ hai của AP;BP;CP và (O). A2;B2;C2 theo thứ tự là điểm đối xứng của A1; B1; C1 qua A0; B0; C0. Chứng minh H, A2, B2, C2 cùng thuộc một đường tròn có tâm thuộc OH.

(Hiện tại em chỉ mới làm được câu bất của anh Huyện với câu hình này, klq nhưng em cũng nhờ đứa bạn chụp lại cái đề này hôm qua ).

Cho $x,y,z\geq 1$; $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}= 2$. Chứng minh:

$\sqrt{x+y+z}\geq \sqrt{1-x}+\sqrt{1-y}+\sqrt{1-z}$.

Ta có: $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2=>\frac{z-1}{z}+\frac{y-1}{y}+\frac{x-1}{x}=1$

Sử dụng BĐT Cauchy-schwarz ta có: $x+y+z=(x+y+z).\sum \frac{x-1}{x}\geq (\sum \sqrt{x-1})^2$

Suy ra ĐPCM