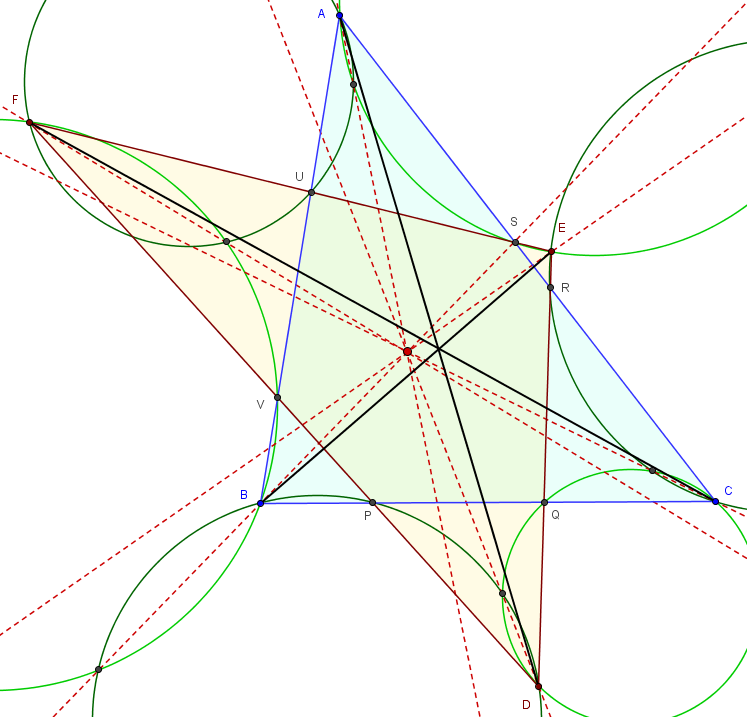
Bài toán. (Đào Thanh Oai)  Cho ngũ giác $A_1A_2A_3A_4A_5$ nội tiếp đường tròn $(O)$. Đặt $B_i=A_{i-1}A_i\cap A_{i+1}A_{i+2}$ với mọi $i\in \overline{1,5}$.

$(O_i)$ là đường tròn qua $B_i,A_{i+2},A_{i+4}.C_i$ là giao điểm thứ hai của $O_{i+1}$ và $(O_{i+4}$.

Khi đó $C_1,C_2,C_3,C_4,C_5$ cũng thuộc một đường tròn.

Bổ sung. (baopbc) a) $A_iC_{i+2}$ đồng quy tại $I$.

b) Gọi $J$ là tâm $(C_1C_2C_3C_4C_5)$. Chứng minh $O,I,J$ thẳng hàng.

Spoiler

Bài toán được chú Đào Thanh Oai đưa lên AopS vào chiều nay, không hiểu vì sao lại bị mất , mình xin được đăng lại tại đây!

Hình vẽ

Một số đặc điểm của đường đối trung được tổng hợp bởi $LuisGonzáles$.

 Đặc trưng của đường đối trung.pdf   131.43K   963 Số lần tải

Tiếp tục nào!

Bài toán. (Tev Cohl) Cho hai tam giác $ABC$ và $DEF$ sao cho $AD,BE,CF$ đồng quy. $P,Q,R,S,U,V$ lần lượt là giao của $BC$ với $FD,BC$ với $DE,CA$ với $DE,CA$ với $EF,AB$ với $EF,AB$ với $FD$. Chứng minh rằng $\odot (BDP),\odot (CDQ),\odot (CER),\odot (AES),\odot (AFU),\odot (BFV)$ có chung tâm đẳng phương.

Hình vẽ bài toán

Một bài rất đẹp nhưng chưa có lời giải!

Cho $f:\mathbb{R}\rightarrow \mathbb{R}$ thỏa mãn: $f(x^n+y^n)=(x+y)(f^{n-1}(x)-f^{n-2}(x)f(y)+...+f^{n-1}(y))\forall x,y\in \mathbb{R},n$ lẻ, $n>1$

Chứng minh rằng $f(ax)=af(x)\forall x\in \mathbb{R}$ và $\forall a\in \mathbb{N}$.

$\textbf{Bài toán.}$ $\textit{(Lim Jeck)}$ $X,Y,Z$ là các điểm nằm trong tam giác $ABC$ sao cho

$\angle BAY=\angle CAZ,\angle CBZ=\angle ABX,\angle ACX=\angle BCY$

Kéo dài $AY,AZ$ cắt $BC$ lần lượt tại $Y_a,Z_a$. Tương tự xác định các điểm $X_b,Z_b,X_c,Y_c$. Giả sử $X_bY_a,Y_cZ_b,Z_aX_c$ đồng quy.

Chứng minh rằng tồn tại các điểm $D,E,F$ lần lượt thuộc các cạnh $BC,CA,AB$ sao cho $X$ thuộc $EF,Y$ thuộc $FD,Z$ thuộc $DE$ và $AD,BE,CF$ đồng quy.

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 3 tháng 11 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán mới,

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn $(K)$ tiếp xúc $CA$, $AB$ và tiếp xúc trong $(O)$.

Gọi $M,N$ lần lượt là trung điểm các cung $CA$, $AB$ chứa $B$, $C$ của $(O)$. $AM$, $AN$ lần lượt cắt $KC$, $KB$ tại $P$, $Q$.

$R$ đối xứng $A$ qua $PQ$. Chứng minh rằng đường tròn ngoại tiếp tam giác $RBC$ tiếp xúc $(K)$.

Hình vẽ bài toán

Cho $ABCD$ là tứ giác nội tiếp. Giả sử $AD$ cắt $BC$ tại $S$. Lấy $I$ thuộc phân giác $\angle DSC$. $AI, BI$ cắt $(O)$ tại $K,L$. Lấy $P$ đối xứng với $C$ qua $OL$. Tương tự lấy điểm $Q$. $R,S$ lần lượt là điểm chính giữa cung nhỏ $DP, QC$. $M,N$ lần lượt là giao của $TP$ với $AR$; $TQ$ với $BS$. ($T$ là điểm chính giữa cung nhỏ $AB$). Chứng minh: $TM=TN$.

Xem tại đây: http://diendantoanho...-olympiad-2016/

Gọi $T$ là trung điểm $BC$. Ta có $MS^2-MB^2=\frac{BE^2}{4}-\frac{BF^2}{4}$, tương tự thì $NC^2-NS^2=\frac{CE^2}{4}-\frac{CF^2}{4}$

$\Rightarrow MS^2-MB^2+NC^2-NS^2=\frac{BE^2}{4}-\frac{BF^2}{4}+\frac{CE^2}{4}-\frac{CF^2}{4}=\frac{BC^2}{4}-\frac{BC^2}{4}=0$

Mặt khác do $TB^2-TC^2=0$ nên $MS^2-MB^2+NC^2-NS^2+TB^2-TC^2=0$

Do đó theo định lí $\text{Carnot's}$, $K$ thuộc đường thẳng qua $T$ vuông góc với $BC$. Do đó $K$ di chuyển trên một đường thẳng cố định.

CHo đường tròn $(O)$.Hai đường tròn $(C1)$ và $(C2)$ tiếp xúc trong với $(O)$ lần lượt tại $A$ và $F$.Hai đường tròn này cắt nhau tại 2 điểm D và E phân biệt.Gọi K là hình chiếu của A lên DE.H là trung điểm của AK.M là trung điểm $DE$.Chứng minh góc $HMK$ bằng $\frac{1}{2}$ số đo cung nhỏ $AF$ của $(O)$.

Bài này không ai giải cả đơn giản là vì đề bị sai! Xem hình sau.

Bài toán này nằm trong chuổi các bài toán mở rộng $IMO$ 2015 của thầy Trần Quang Hùng, phép chứng minh tham khảo link dưới.

https://www.dropbox....ay1170.pdf?dl=0

Bổ đề. Cho $p$ là số nguyên tố có dạng $4k+3$. Khi đó $p\mid x^2+y^2\iff p\mid x,p\mid y$.

Chứng minh. Dễ thấy chỉ cần chứng minh cho trường hợp cả hai số không chia hết cho $p$. Theo định lí $Fermat$ nhỏ thì:

$x^{p-1}\equiv y^{p-1}\equiv 1\pmod p\implies x^{p-1}+y^{p-1}\equiv 2\pmod p\implies x^{4k+2}+y^{4k+2}\equiv 2\pmod p$

$\iff (x^2)^{2k+1}+(y^2)^{2k+1}\equiv 2 \pmod p$ (mâu thuẫn do $p\mid x^2+y^2$. Bổ đề được chứng minh.

Quay lại bài toán. Giả sử $A=\frac{x^2+y^2}{x+y}$ có ước nguyên tố $p$ có dạng $4k+3\implies p\mid x^2+y^2$.

Theo bổ đề trên thì $p\mid x,p\mid y$. Đặt $x=pa,y=pb$ thì $A=p(\frac{a^2+b^2}{a+b})$.

Do đó ta chỉ cần xét trong trường hợp $A$ không có ước nguyên tố dạng $4k+3$.

Do $A\mid 1978=2.3.11.17$ nên ta xét với $A=1$ hoặc $A=2$.

Nếu $A=1$ thì $x^2+y^2=x+y$, do $x,y$ nguyên nên $x^2+y^2\geq x+y$. Dấu $"="$ xảy ra $\iff x=y=1.$

Nếu $A=2$ thì $x^2+y^2=2x+2y$, do $x,y$ nguyên nên dễ thấy $x=y=2$. Do đó $x=y.\ \blacksquare$

$\textbf{Lời giải.}$ Ta có $\angle A_2C_1A=\angle A_2B_1A,\angle A_2BC_1=\angle A_2CB_1$ nên $\triangle A_2C_1B\sim \triangle A_2B_1C$ (góc - góc). Do đó

\[\frac{A_2B}{A_2C}=\frac{BC_1}{CB_1}\]

Suy ra \[\frac{A_4B}{A_4C}=\frac{[BA_2A_3]\cdot CA_2}{[CA_2A_3]\cdot BA_2}=\frac{BA_3\cdot CA_2}{CA_3\cdot BA_2}=\frac{BA_3\cdot CB_1}{CA_3\cdot BC_1}\]

Từ đây áp dụng định lí $\text{Ceva}$ cho $\triangle ABC$ với $AA_1,BB_1,CC_1$ và $AA_3,BB_3,CC_3$ đồng quy ta suy ra

\[\prod \frac{A_4B}{A_4C}=1\]

Do đó theo bổ đề $\text{Ceva}$ trong đường tròn ta suy ra $AA_4,BB_4,CC_4$ đồng quy.

PS. Kỳ thực nếu sử dụng lượng giác thì sẽ gọn hơn!

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có $H$ là trực tâm,đường cao $AD$.Gọi $K$ đối xứng $B$ qua $D.KH$ cắt $AC$ tại $Q$.Chứng minh rằng: $\widehat{QDO}=90^{\circ}$

Lời giải. 

______

baopbc

Bạn chép sai đề rồi, đề đúng phải là: Cho tam giác $ABC$ nội tiếp $(O)$ có $AC$ là đường kính. $H$ là hình chiếu của $B$ lên $AC$. $T$ là giao điểm của tiếp tuyến tại $B,C$ của $(O)$. Chứng minh: $AT$ chia đôi $BH$.

Chứng minh: $CT$ cắt $AB$ tại $K$. Do $\triangle CBK$ vuông tại $B$, $TB=TC$ nên $BT$ là đường trung tuyến ứng với cạnh huyền của tam giác vuông $CBK$.

$\Rightarrow T$ là trung điểm $CK$. Do $BH//CK$ nên theo định lí hình thang ta có điều phải chứng minh.

Lời giải: Để ý rằng: $DCAB$ là tứ giác nội tiếp. Gọi $L$ là giao của $CD$ với $AB$. Bằng biến đổi tỉ số, dễ thấy rằng: $L,B$ liên hợp.

Bài toán biến thành bài toán sau: Cho $ABCD$ là tứ giác nội tiếp. $AD,BC$ cắt nhau tại $E$. $AC,BD$ cắt nhau tại $F$. Khi đó điểm $Miquel$ của tứ giác toàn phần $ABCDEF$ là hình chiếu của $O$ lên $EF$. Bài toán là một mở rộng quen thuộc của bài 5 - IMO 1985 kết hợp với định lí $Brocard$.

P.s: Bài này cũng có trong nhiều tài liệu tham khảo, em xin không chứng minh ở đây!

 

Cho $x_{1}, x_{2}, x_{3}, ..., x_{100}$ là các số có tổng chia hết cho 6

CM: $A= x_{1}^{3} + x_{2}^{3} + x_{3}^{3} + .... + x_{100}^{3}$ chia hết cho 6

 

Ta có: $x^{3}\equiv x(mod 2);x^{3}\equiv x(mod 3)$ nên $x^{3}\equiv x(mod 6)$. Ta có đpcm./

Cho em hỏi kí hiệu này là gì ạ?

$\binom{k}{n}$

Đây là tính chất quen thuộc về đường đẳng giác, bạn có thể tham khảo tại đây: 

http://diendantoanho...bài-toán/page-9

(post #170)

Bài toán này mình tìm ra một cách tình cờ và thấy rằng đây đúng là một bài toán đẹp! Nếu như bài toán này đã trùng lặp ở đâu thì mong mọi người thứ lỗi cho sự hấp tấp của mình!

Bài toán: Cho lục giác $ABCDEF$ nội tiếp $(O)$. Các đường thẳng $AB,BC,CD,DE,EF,FA$ cắt nhau tạo thành $6$ điểm $X,Y,Z,U,V,W$ bên ngoài đường tròn. Chứng minh rằng: $XU, YV, ZW$ đồng quy.

Hình vẽ bài toán

Một bài chắc quen thuộc.

Bài toán. Cho tam giác $ABC$ nội tiếp $\odot (O)$, ngoại tiếp $\odot (I)$. Chứng minh rằng trục đẳng phương của $\odot (A;AI)$ và $\odot (O)$ tiếp xúc $\odot (I)$.

Hình vẽ bài toán

Mình đã đưa bài toán lên AopS và nhận được lời giải của EinsteinXXI tại đây.

Cho đoạn thẳng $BC. E$ là trung điểm $BC,D$ là trung điểm $EC$. Trên trung trực đoạn $CE$ lấy $F$ bất kỳ. $A$ thuộc tia đối tia $FC$ sao cho $FC=3FA. (AEC)$ giao $AB$ lần hai tại $G$. Chứng minh $EG$ vuông góc $GF$.

Lời giải.

Bài toán. Cho tam giác $ABC$. Một đường tròn bất kì qua $B,C$ cắt $AC,AB$ lần lượt tại $E,F$. Đường thẳng qua $E,F$ lần lượt vuông góc với $AC,AB$ cắt nhau tại $O$. Lấy $M,N$ bất kì trên $EO,FO$ theo thứ tự đó. Kẻ $CQ\perp AM,BP\perp AN. BP$ và $AM$ cắt nhau tại $I$. $MB$ cắt $NC$ tại $K$.

Chứng minh rằng: $\overline{O,I,K}$

Hình vẽ bài toán

Nguồn: Own

Lời giải của em thế này ạ!

Bất đẳng thức đã cho tương đương với:

$a^{2}+b^{2}+c^{2}-6+2abc(a+b+c)-3a^{2}b^{2}c^{2}\geq 0$( do $ab+bc+ac=3$)

$\Leftrightarrow (a+b+c)^{2}+2abc(a+b+c)-3a^{2}b^{2}c^{2}\geq 12$

$\Leftrightarrow (a+b+c-abc)(a+b+c+3abc)\geq 12 (*)$

Do $ab+bc+ca=3$ nên $a+b+c\geq 3,abc\leq 1$

Đặt $a+b+c=3+x$, $abc=1-y$ thì $x,y\geq 0$ và $y< 1$

$(*)\Leftrightarrow (2+x+y)(6-y+x)\geq 12$

$\Leftrightarrow x^{2}-y^{2}+8x+4y\leq 0$

Do $y< 1$ nên bất đẳng thức cuối đúng, vậy ta có đpcm./