Tìm kiếm
Nam
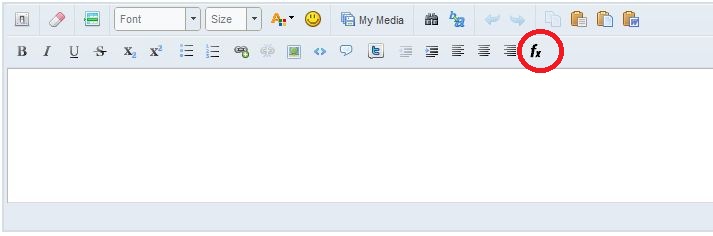
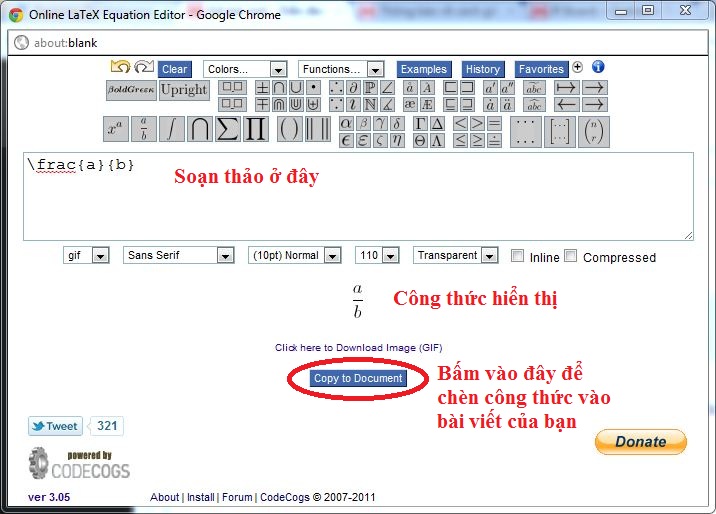
Gửi bởi Dưới đây là một số ví dụ. Nếu các bạn muốn gõ thử thì xin mời nhấn vào đây.
$\dfrac{a}{b+c}$
$\frac{a}{b+c}$$a^2+b_i^3 \ge c_{i+1}^5+d_{x+1}^{y+1}$
$a^2 + b_i^3 \ge c_{i+1}^5 + d_{x+1}^{y+1}$$\sqrt{a+b^2}$
$\sqrt{a+b^2}$$\sqrt[n]{a+b}$
$\sqrt[n]{a+b}$$\sum_{k=1}^n \dfrac{1}{k^2}$
$\sum_{k=1}^n \frac{1}{k^2}$$$\sum_{k=1}^n \dfrac{1}{k^2}$$
$$\sum_{k=1}^n \frac{1}{k^2}$$$\lim_{x \rightarrow 0} \dfrac{\sin x}{x}=1$
$\lim_{x \rightarrow 0} \frac{\sin x}{x}=1$$$\lim_{x \rightarrow 0} \dfrac{\sin x}{x}=1$$
?$$\lim_{x \rightarrow 0} \frac{\sin x}{x}=1$$$\lim_{n \to \infty}\sum_{k=1}^n \dfrac{1}{k^2}= \dfrac{\pi^2}{6}$
$\lim_{n \to \infty}\sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6}$$$\lim_{n \to \infty}\sum_{k=1}^n \dfrac{1}{k^2}=\dfrac{\pi^2}{6}$$
$$\lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6}$$$\int_{0}^{\pi/2} f(x)dx$
$\int_{0}^{\pi/2} f(x)dx$$$\int_{0}^{\dfrac{\pi}{2}} f(x)dx$$
$$\int_{0}^{\dfrac{\pi}{2}} f(x)dx$$$\underbrace{ a+b+\cdots+z }_{26}$
$\underbrace{ a+b+\cdots+z }_{26}$$x\equiv a \pmod{b}$
$x\equiv a \pmod{b}$$1 + \left( \dfrac{1}{1-x^2} \right)^3$
$1 + \left( \dfrac{1}{1-x^2} \right)^3$$\left\{\begin{array}{l} x+y = 1 \\ x - y =1 \end{array}\right.$
$\left\{\begin{array}{l}x+y = 1 \\x - y =1 \end{array}\right.$$\mathbf{X}=\left( \begin{array}{ccc}x_{11} & x_{12} & \ldots \\ x_{21} & x_{22} & \ldots \\ \vdots & \vdots & \ddots \end{array} \right)$
$\mathbf{X}=\left( \begin{array}{ccc}x_{11} & x_{12} & \ldots \\ x_{21} & x_{22} & \ldots \\ \vdots & \vdots & \ddots \end{array} \right)$\begin{eqnarray}f(x) &=& \cos x \\ f'(x) &=& -\sin x \\ \int_{0}^{x} f(y)dy &=& \sin x \end{eqnarray}
\begin{eqnarray}f(x) &=& \cos x \\ f'(x) &=& -\sin x \\ \int_{0}^{x} f(y)dy &=& \sin x \end{eqnarray}(sẽ tiếp tục cập nhật)
- NguyThang khtn, perfectstrong, Zaraki và 34 người khác yêu thích
