DaiphongLT

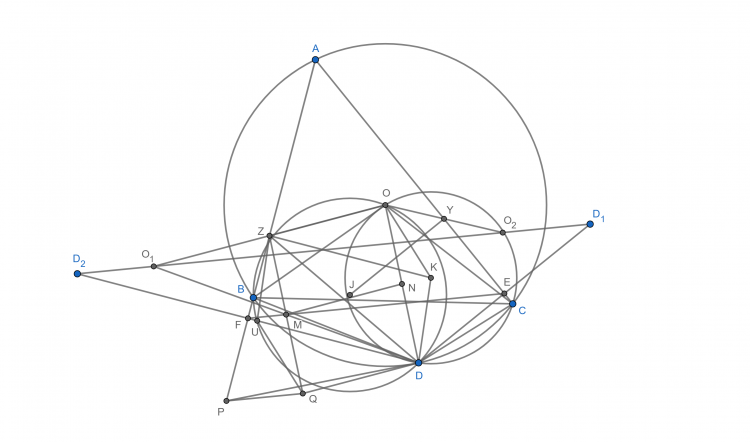
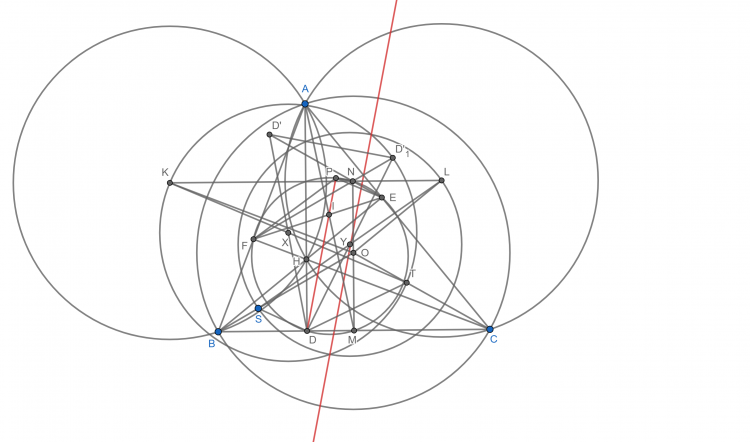
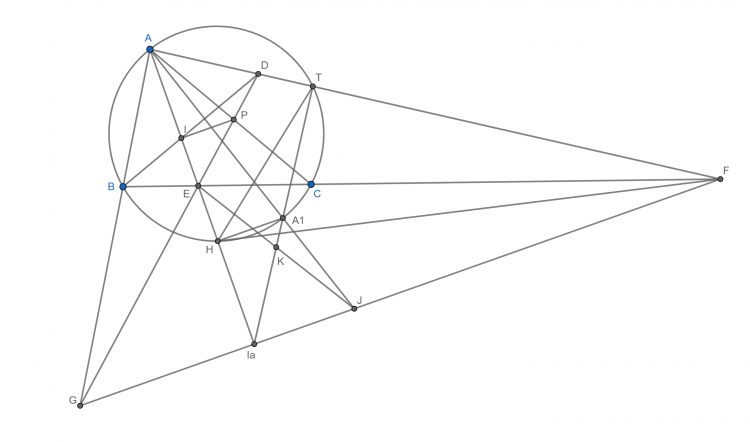
Bài 36. Cho tam giác ABC nội tiếp đường tròn (O). Gọi I, Ia lần lượt là tâm đường tròn nội tiếp, tâm đường tròn bàng tiếp góc A của tam giác ABC. Gọi AA1 là đường kính của đường tròn (O). IaA1 cắt lại đường tròn (O) tại T, AI cắt BC tại E và đường thẳng qua I vuông góc với AE cắt AC tại P. Chứng minh rằng AT, EP và BI đồng quy

Gọi $G$ thuộc $AB$ sao cho $I_aG//IP$, ta có $\Delta AI_aG \sim \Delta AIP (g-g)$ nên $\frac{I_aG}{IP}=\frac{AI_a}{AI}=\frac{EI_a}{EI}$ hay $P, E, G$ thẳng hàng. Gọi $GI_a$ cắt $AA_1$ và $BC$ tại $J$ và $F$, $I_aA_1$ cắt $EJ$ tại $K$. Menelaus cho tam giác $JEA$ cát tuyến $A_1, K, I_a$ ta sẽ được $K$ trung điểm $EJ$. Biến đổi góc đơn giản dễ thấy $AEJF$ nội tiếp. Do đó $\widehat{EAF}=\widehat{EJI_a}=\widehat{KI_aJ}=\widehat{HA_1K}=\widehat{EIT}$ hay $A, T, F$ thẳng hàng. Để ý $(AE, II_a)=-1$ nên $BI, EP, AT$ đồng quy.

Bài 33. Cho tam giác $ABC$ nội tiếp $(O)$ và điểm $P$ bất kỳ trên $(O)$. $J,K$ là tâm đường tròn $(BOP)$ và $(COP)$. $Y,Z$ là hình chiếu của $J,K$ lên $AC,AB$. Chứng minh $YZ$ đi qua 1 điểm cố định khi $P$ di chuyển trên $(O)$

Dựng hình bình hành $OZQD$ và $DKZU$, khi đó $OKQU$ cũng là hình bình hành. Vì $KO=KD$ nên $UZ=UQ$. Gọi $(U,UV)$ cắt $AB$ tại $P$, $E$ và $F$ là hình chiếu của $D$ lên $CA$ và $AB$.
Ta có $\Delta UZQ=\Delta KOD(c-c-c)\Rightarrow \widehat{ZPQ}=\widehat{OCD}=90^{\circ}-\widehat{DAC}=\widehat{AFE}\Rightarrow PQ//EF$, mặt khác $UD//KZ$ nên $DU$ vuông $AB$ hay $D, U, F$ thẳng hàng. Do đó $Z$ và $P$ đối xứng với nhau qua $DF$. Vì vậy nếu gọi $M$ trung điểm $ZQ$ thì ta có $FM//PQ//FE$ nên $F, M, E$ thẳng hàng
Gọi $N$ trung điểm $OD$, khi đó ta có $MNOZ$ là hình bình hành, do đó nếu ta gọi $DM$ cắt $OZ$ tại $O_1$ thì ta có $ZM$ là đường trung bình của tam giác $O_1OD$. Gọi $D_1, D_2$ lần lượt là điểm đối xứng của $D$ qua $CA, AB$, vì $M$ trung điểm $OD_1$ nên $O_1$ thuộc $D_1D_2$, định nghĩa $O_2$ tương tự $O_1$, ta cũng có $O_2$ thuộc $D_1D_2$, do đó $O_1O_2$ là đường thẳng Steiner của $D$ đối với tam giác $ABC$ hay $O_1O_2$ đi qua trực tâm tam giác $ABC$. Đến đây xét phép vị tự tâm $O$, tỉ số $\frac{1}{2}$, ta được $YZ$ đi qua tâm Euler của tam giác $ABC$

Bài 35. Cho hình bình hành $ABCD$ có $P$ là điểm bất kỳ trên $AB$. $DP,CP$ lần lượt cắt $CB$ và $AD$ tại $E,F$. $G$ là tâm vị tự trong của đường tròn nội tiếp hai tam giác $PAE$ và $PBF$. Chứng minh $PG$ đi qua điểm Nagel của tam giác $PCD$. 

Gọi $I, I'$ lần lượt là tâm nội tiếp tam giác $PAE$ và $PBF$. $M, N$ lần lượt là giao điểm của $PI', PI$ với $CD$, $S$ là tiếp điểm của đường tròn nội tiếp tam giác $PCD$ với $BC$, $T$ là điểm đối xứng của $S$ qua trung điểm $CD$
Dễ thấy $DM=DP$ và $CN=CP$. Khi đó $PD-PC=SD-SC$ hay $PD+SC=SD+PC$ nên $DM+TD=TC+CN$. Do đó $TM=TN$ hay $T$ trung điểm $MN$
Gọi $II'$ cắt $BC$ tại $K$, $PT$ cắt $II'$ tại $G'$ thì ta có $(II', G'K)=P(II', G'K)=P(NM,TK)=-1$. Mặt khác $K$ là tâm vị tự ngoài của $(I)$ và $(I')$ nên $G'$ là tâm vị tự trong. Do đó có đpcm

góp vui

Bài toán 6. Trên cạnh $\displaystyle AB$ của ngũ giác $\displaystyle ABCDE$ lấy điểm $\displaystyle F$ sao cho $\displaystyle \Delta ADE\sim \Delta ECF\sim \Delta DBC$. Chứng minh rằng $\displaystyle \frac{AF}{BF} =\frac{EF^{2}}{CF^{2}}$.

Gọi $K$ là giao điểm của $AD$ và $CF$, dễ thấy $K$ thuộc $(DEC)$, định nghĩa $L$ tương tự ta cũng có $L$ thuộc $(DEC)$ hay $D, E, K, L , C$ đồng viên
Ta có $\frac{AF}{BF}=\frac{sin \widehat{AKF}.KF}{sin \widehat{DAB}}.\frac{sin \widehat{DBA}}{sin \widehat{FLB}.FL}=\frac{DA}{DB}.\frac{DC}{DE}.\frac{EF}{CF}=\frac{EF}{FC}.\frac{EC}{CF}.\frac{EF}{CE}=\frac{EF^2}{CF^2}$

 

$\textbf{Bài toán 32.}$ Cho $\Delta ABC$ nhọn, không cân nội tiếp đường tròn $(O)$. Ba đường cao $AD,BE,CF$ cắt nhau tại $H$. $AO$ cắt $EF$ tại $J$. Gọi $M$ là trung điểm của $BC$. $JD$ cắt $HM$ tại $S$. 

a) Chứng minh rằng $OS$ đi qua tâm đường tròn ngoại tiếp $\Delta JDM$

b) Giả sử $(AJD)$ cắt $(O)$ tại điểm thứ hai $K$. Gọi $I$ là điểm đối xứng với $A$ qua $(O)$, $G$ là giao điểm thứ hai của $(ADJ)$ và $(AEF)$. Chứng minh rằng $GI$ và $HK$ cắt nhau tại một điểm trên $EF$.

c) Gọi $N$ là giao điểm của đường trung bình đối diện cạnh $BC$ của $\Delta ABC$ với $AD$. $ON$ cắt $(ODM)$ tại điểm thứ hai $P$. Dựng hình bình hành $DMQP$. Chứng minh rằng $Q$ thuộc đường tròn Euler của $\Delta ABC$.

 

$a)$, Gọi $L, T$ là giao điểm của $EF$ với $BC, HM$. $K$ trung điểm $EF$. Ta có $HK//DJ$ nên $\widehat{TJD}=\widehat{TKH}=\widehat{HMD}$ nên $TJMD$ nội tiếp. Do đó biến đổi góc đơn giản ta được $OL$ vuông góc $TD$. Gọi $X$ là giao 2 tiếp tuyến tại $B, C$ của $(O)$ thì ta được $T, D, X$ thẳng hàng. Kẻ tiếp tuyến $LX, LY$ tới $(O)$, vì $(LD, BC)=-1$ nên $X, D, Y$ thẳng hàng. Mặt khác $L, Z, J, O, M, Y$ đồng viên (đường tròn đường kính $OL$) nên nếu gọi $G$ là giao điểm của $TD$ và $JM$ thì ta có được $GY.GZ=GM.GJ$ hay $G$ nằm trên trục đẳng phương của $(JDM)$ và $(O)$, mặt khác $LD.LM=LB.LC$ nên $L$ thuộc trục đẳng phương của $(JDM)$ và $(O)$. Vì vậy $LG$ là trục đẳng phương của $(JDM)$ và $(O)$, gọi $W$ là tâm $(JDM)$ thì ta có $OW$ vuông $LG$, mặt khác $WS$ vuông $LG$ (Brocard) nên $O, W, S$ thẳng hàng.


$b)$ Gọi $HM$ cắt $EF$ tại $T$, dễ thấy $A, T, K$ thẳng hàng, gọi $GI$ cắt $EF$ tại $S$, $AS$ cắt $(JMS)$ tại $U$, ta sẽ chứng minh $T, S, U, D$ đồng viên. Phần này đơn giản là chỉ biến đổi góc, sau đó sử dụng phép nghịch đảo cực $A$ phương tích $AH.AD$ là được

$c)$ Gọi $I, J, K$ trung điểm $PM, DA, AH$. Ta có $\Delta PDM\sim \Delta DGO (g-g)$ hay $\Delta PDI \sim \Delta DGJ (c-g-c)$. Do đó $\widehat{DQM}=\widehat{PDI}=\widehat{DGJ}=\widehat{MKD}$ nên có đpcm 

 

Cho tam giác $ABC$ có $l$ là tâm nội tiếp và $Fe$ là điểm Feuerbach của đường tròn nội tiếp và đường tròn Euler tam giác $ABC$. Chứng minh đường tròn Euler của các tam giác $IBC,ICA, IAB$ đồng quy tại điểm $Fe$.

 

Gợi ý: - Gọi $(I)$ tiếp xúc với $BC, CA, AB$ tại $D, E, F$, $M$ trung điểm $BC$. Chứng minh $\Delta F_eDM\sim \Delta AIO$ 
           - Gọi $BI$ cắt $EF$ tại $J$. Tính $\widehat{DJM}$ theo các góc của tam giác $ABC$ để chỉ ra $\widehat{DJM}=\widehat{IAO}$. Từ đó có được đpcm
         

Bài 26: Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O)$ có các đường cao $AD, BE, CF$ đồng quy tại $H$. $K, L$ lần lượt là tâm $(HAB)$ và $(HAC)$. $S, T$ là hai điểm thuộc $OB, OC$ sao cho $DH$ là phân giác $\widehat{SDT}$. $X, Y$ lần lượt là trung điểm $KT, LS$. $I$ là giao điểm của đường trung tuyến đỉnh $A$ trong tam giác $ABC$ với $EF$. Chứng minh $DI$ song song với trục đẳng phương của $(X, XK)$ và $(Y, YL)$.
P/s: đây là một bài toán mình mở rộng từ một bài toán của anh Phan Quang Trí, phát biểu có vẻ dễ hơn bài ban đầu:))

Gọi $M$ trung điểm $BC$, $OM, DI$ cắt $(DEF)$ tại $N,P$. Ở đây ta dễ thấy rằng $K, L$ là điểm đối xứng của $O$ qua $AB, AC$ do đó $KL$ đi qua $N$.
Gọi $D', D'_1$ lần lượt là điểm đối xứng của $D$ qua $X, Y$. Ở đây ta dễ thấy rằng $KNCD$ là hình bình hành do đó $D'ECT$ là hình bình hành hay $D',N, E$ thẳng hàng. Tương tự ta cũng có $D'_1, N, F$ thẳng hàng.
Ta có $D'N//OC$ và $D'_1N//OB$ do đó $\widehat{D'ND'_1}=\widehat{BOC}=\widehat{EPF}$. Lại có $\frac{D'N}{D'_1N}=\frac{TC}{SB}=\frac{DC}{DB}=\frac{PF}{PE}\Rightarrow \Delta PEF\sim \Delta ND'_1D'(c-g-c)$ hay $PN//D'D'_1$. Nói cách khác $DI$ vuông góc $XY$. Từ đây ta có đpcm

để topic tiếp tục hoạt động ( vì bài trên có vẻ hơi quá tầm với mn....)  mình xin post bài mới

Bài 31. Cho tam giác $ABC$ và điểm $M$ bất kỳ nằm trên trung trực $BC$. $X,Y$ là tâm đường tròn nội tiếp tam giác $ABM$ và $ACM$. Chứng minh $(AXY)$ luôn đi qua 1 điểm cố định

Xét phép nghịch đảo đối xứng cực $A$ phương tích $AB.AC$ đưa về bài toán như sau: Cho $\Delta ABC$, $M$ bất kì nằm trên đường tròn $A-Apollonius$, $X, Y$ là tâm bàng tiếp tam giác $ABM, ACM$. Chứng minh $XY$ đi qua một điểm cố định.
Ở đây $XY$ đi qua giao điểm của chân đường phân giác ngoài $\widehat{BAC}$ với $BC$

Bài 30: Cho tam giác $ABC$, trực tâm $H$. $G, N_a$ là điểm Gergone, Nagel của tam giác $ABC$. $K$ là điểm liên hợp đẳng cự với $H$ trong tam giác $ABC$. Chứng minh $GN_a$ đi qua $K$

Cho tam giác ABC. (O) bất kì qua B,C cắt AB,AC lần lượt tại F,E. (AEB) cắt (AFC) tại I khác A. (AEB) cắt CF tại M (F nằm giữa C,M). (AFC) cắt BE tại N (E nằm giữa B,N). Đường thẳng qua M vuông góc AM cắt BE tại U, đường thẳng qua N vuông góc AN cắt CF tại V. 

CMR: MN,UV,OI đồng quy

Gợi ý: - Gọi $X, Y$ trung điểm $BF, CE$. Chứng minh $A, X, I, Y$ đồng viên (tỉ số phương tích) để có được $\widehat{AIO}=90^{\circ}$
           - Kẻ đường kính $AK, AL$ của $(ABE), (ACF)$, $J$ là giao điểm của $KM, LN$. Chứng minh $KN, PJ, ML$ đồng quy. Chứng minh bằng cách gọi $Q, R$ lần lượt là giao điểm của $JP, KL$ với $MN$. Khi đó cần chứng minh $(RQ, NM)=-1$. Chú ý $AN=AM$ và sử dụng phép nghịch đảo cực $A$ phương tích $=AP.AI$ (gợi ý tiếp như hình vẽ).
                   

Bài 28. Cho tam giác $ABC$ nhọn và điểm $D$ bất kỳ di động trên $BC$ sao cho $AD$ không vuông góc $BC$. Giả sử tồn tại hai điểm $E,F$ trên $AC,AB$ sao cho $\angle ADB = \angle BEC = \angle CFA$. $AD,BE,CF$ cắt nhau tạo thành tam giác $XYZ$. Chứng minh trực tâm tam giác $XYZ$ di động trên 1 đường tròn cố định khi $D$ di động

Gọi $O, H$ lần lượt là tâm ngoại tiếp, trực tâm tam giác $ABC$, $H'$ là trực tâm giác $XYZ$. Dễ thấy $\Delta XYZ\sim \Delta ABC(g-g)$
Dễ chứng minh được $X, Y, Z$ thuộc $(BHC), (CHA), (AHB)$. Do đó $H$ là tâm $(XYZ)$
Gọi $N$ là điểm đối xứng của $H$ qua trung trực $BC$. Khi đó ta có $(XN, XH)$ $+$ $(XH, AD)$ $\equiv$ $(CN,CH)$ $+$ $(AO,CB)$ $\equiv$ $(CN,CB)$ $-$ $(CH, CB)$ $+$ $(AO,CB)$ $\equiv$ $(CA,CB)$ $+$ $(CB,BH)$ $\equiv$ $\frac{\pi }{2}$ (mod $\pi$)
Vì vậy  $XN$ vuông $AD$ hay $X, H', N$ thẳng hàng. Ở đây $\Delta AHO\sim \Delta XH'H$ nên $(H'H, H'X)=(HO,HA)=\frac{1}{2}(OH,ON)$ (mod $\pi$) hay $H'$ nằm trên $(O,OH)$.              

Bài 27. Cho tam giác $ABC$ nội tiếp $(O)$ và ngoại tiếp $(I)$ có $P$ là điểm chính giữa cung $BC$ nhỏ. $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. và $(AEF)$ cắt $(O)$ tại $Z$ khác $A$. $ZP$ cắt $(I)$ tại $Q$ và $AQ$ cắt $(I)$ tại $T$. $K$ là giao điểm của đường cao $AH$ và đường thẳng Simson của $P$ đối với tam giác $ABC$. Chứng minh $(ATK)$ tiếp xúc $(I)$

Gọi $R, U$ trung điểm $EF, BC$, $L$ là điểm chính giữa cung lớn $BC$ của $(O)$. $AQ$ cắt $EF$ tại $N$, $IN$ cắt $(AEF)$ tại $M$,
Xét phép nghịch đảo cực $I$, pt $=ID^2$, ta có được $(AMT)\leftrightarrow (RNT)$, $(I)\leftrightarrow (I)$           
Kẻ tiếp tuyến tại $T$ của $(I)$ cắt $EF$ tại $V$. Vì $(QT, EF)=-1$ nên $VQ$ cũng là tiếp tuyến của $(I)$. Do đó $(VN, FE)=-1$ hay $VT^2=VF.VE=VN.VR$ (Maclaurin). Do đó $(RNT)$ tiếp xúc $(I)$ hay $(AMT)$ tiếp xúc $(I)$. Vì vậy ta cần chứng minh $K\in (AMT)$
Gọi $S$ là giao điểm của $PD$ với $AK$, $D'$ đối xứng với $D$ qua $(I)$, tiếp tuyến tại $D'$ của $(I)$ cắt $AK$ tại $H$. Ta sẽ chứng minh $H, R, I, K$ đồng viên.
Dễ thấy $S$ thuộc $(AEF)$ và $Q, H, D', I, S$ đồng viên
Ta có $ALUK$ là hình bình hành, $\Delta LUC\sim \Delta ARE\Rightarrow \frac{LC}{AE}=\frac{LU}{AR}=\frac{AK}{AR}$. Vì vậy ta cần chứng minh $\frac{AI}{AH}=\frac{LC}{AE}$ $(1)$
Dựng hình chữ nhật $AHD'X$, $AD'$ cắt $LU$ tại $J$, tính chất quen thuộc là $IJ//BC$ nên $IJUD$ là hình chữ nhật. Ta có $\frac{AD'}{XD'}=\frac{D'J}{ID'}$ $(2)$.
Ở đây $AH=XD'$ nên từ $(1)$ và $(2)$ thì ta cần chứng minh $\frac{AI}{AD'}=\frac{LC}{AE}.\frac{ID'}{D'J}\Leftrightarrow \frac{PI}{D'J}=\frac{LC}{AE}.\frac{ID'}{D'J}\Leftrightarrow \frac{PI}{LC}=\frac{ID}{AE}\Leftrightarrow \frac{PC}{LC}=\frac{IE}{AE}$ (hiển nhiên đúng)
Do đó ta có được $\frac{AK}{AR}=\frac{AI}{AH}$ hay $H, R, I, K$ đồng viên nên $AH.AK=AE^2$
Gọi $AK$ cắt $EF$ tại $Y$, xét phép nghịch đảo cực $A$ pt $= AE^2:$ $H\leftrightarrow K,I\leftrightarrow R,Q\leftrightarrow T,S\leftrightarrow Y$ mà $HIQS$ nội tiếp nên $YRKT$ nội tiếp
Để ý $T, M, Q, R, I$ đồng viên do đó $\widehat{TKA}=\widehat{TRY}=90^{\circ}-\widehat{TRI}=90^{\circ}-\widehat{TMI}=180^{\circ}-\widehat{AMT}$ hay $K\in (AMT)$. Do đó có đpcm.

 

Bài 26: Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O)$ có các đường cao $AD, BE, CF$ đồng quy tại $H$. $K, L$ lần lượt là tâm $(HAB)$ và $(HAC)$. $S, T$ là hai điểm thuộc $OB, OC$ sao cho $DH$ là phân giác $\widehat{SDT}$. $X, Y$ lần lượt là trung điểm $KT, LS$. $I$ là giao điểm của đường trung tuyến đỉnh $A$ trong tam giác $ABC$ với $EF$. Chứng minh $DI$ song song với trục đẳng phương của $(X, XK)$ và $(Y, YL)$.
P/s: đây là một bài toán mình mở rộng từ một bài toán của anh Phan Quang Trí, phát biểu có vẻ dễ hơn bài ban đầu:))

Một bài toán mình được học thấy khá hay, có thể mọi người từng gặp:

Bài 25: Cho tam giác $ABC$ không cân nội tiếp $(O)$, trọng tâm $G$. Kẻ ba đường cao $AD,BE,CF$. Các tia $GD,GE,GF$ cắt $(O)$ tại $X,Y,Z$, $AG,BG,CG$ cắt $(O)$ tại $M,N,P$. Các đường thẳng $MX,NY,PZ$ cắt nhau tạo thành tam giác $A'B'C'$. Chứng minh rằng $A'X, B'Y, C'Z$ cắt nhau tại một điểm nằm trên đường thẳng $OG$.

Đầu tiên ta sẽ chứng minh $AX, BY, CZ$ đồng quy
Gọi $Q$, $R$ là các điểm thuộc $(O)$ thoả mãn $AQ//BC$ và $BR//AC$. Dễ thấy $X, D, G, Q$ và $Y, E, G, R$ thẳng hàng
Gọi $AD, BE$ cắt (O) tại $D', E'$. Pascal $\begin{pmatrix} A & Y& Q \\ B & X& R \end{pmatrix}$ và $\begin{pmatrix} A & Q& E' \\ B & R& D' \end{pmatrix}$. Ở đây ta dễ thấy $QD'$ và $RE'$ đều đi qua $O$. Do đó ta có được giao điểm của $AX$ và $BY$ là một điểm thuộc đường thẳng Euler. Chứng minh tương tự, ta được $AX, BY, CZ$ đồng quy tại một điểm thuộc đường thẳng Euler.
Quay lại bài toán, định nghĩa $J$ tương tự $Q, R$. Pascal $\begin{pmatrix} P&Y &B \\ N&Z &C \end{pmatrix}$ và $\begin{pmatrix} Y &B& J\\ Z &C& R \end{pmatrix}$. Ở đây giao điểm của $BR$ và $CJ$ là điểm đối xứng với $A$ qua trung điểm $BC$. Vì vậy ta có được $A', A, G$ thẳng hàng. Tương tự ta thu được $AA', BB', CC'$ đồng quy tại $G$. 
Do đó $\frac{XB'}{XC'}=\frac{sin\widehat{BGD}}{sin\widehat{CGD}}.\frac{GB'}{GC'}=\frac{BD}{CD}.\frac{GC}{GB}.\frac{GB'}{GC'}$. Tương tự cho các cặp còn lại, ta có được $A'X, B'Y, C'Z$ đồng quy. Desargues cho $\Delta A'AX$ và $\Delta C'CZ$ ta thu được giao điểm của $A'X$ và $C'Z$ là một điểm thuộc đường tròn Euler (theo phần chứng minh ở trên). Do đó ta có được đpcm                

Đây là bổ đề Protassov, bạn có thể tìm kiếm ở trang web thầy Nguyễn Văn Linh