William Nguyen

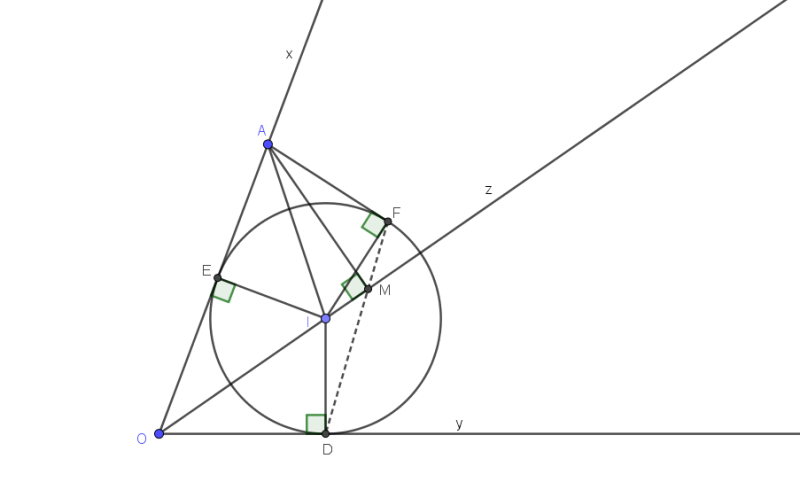
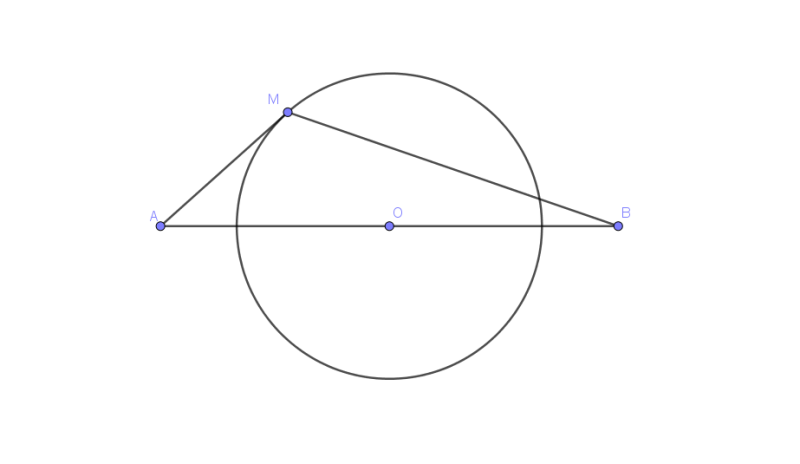
Tình cờ phát hiện thêm nhưng chưa chứng minh được: Khi $M$ thoả mãn đẳng thức $\cos\alpha=\frac{1}{2}OM\left(\frac{1}{OA}-\frac{1}{OB}\right)$ thì $MO$ là đường phân giác $\bigtriangleup MAB.$

 

Mình chứng minh ý này như sau (trong TH OA<OB, với OA=OB là bài toán gốc và OA>OB tương tự):

 

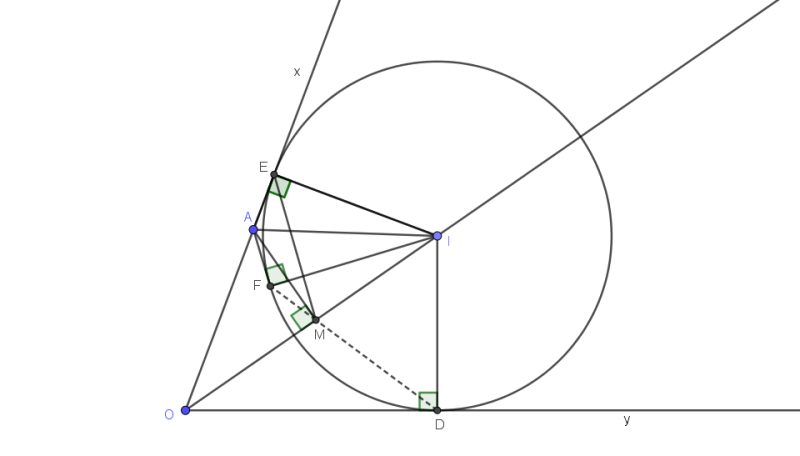
Đường thẳng qua A song song MB cắt tia MO tại C. Gọi D là trung điểm MC thì ta có $\frac{OM}{OB}=\frac{ON}{OA}$ và $OM-ON=2OD$.

 

      $\cos\alpha=\frac{1}{2}OM\left(\frac{1}{OA}-\frac{1}{OB}\right)$

$\Leftrightarrow \cos\alpha=\frac{1}{2}.\left(\frac{OM}{OA}-\frac{ON}{OA} \right)$

$\Leftrightarrow \cos\alpha=\frac{OD}{OA}$

$\Leftrightarrow AD \perp MN$

$\Leftrightarrow \widehat{AMO}=\widehat{ANO}$

$\Leftrightarrow \widehat{AMO}=\widehat{BMO}$ hay $MO$ là phân giác góc $AMB$.

Bài toán gốc:

 

Trường hợp GTNN thì dễ rồi

 

Trường hợp GTLN, mình trình bày cách làm khác bạn leonguyen một chút:

 

Khi $M$ không trùng một trong hai giao điểm của $AB$ với đường tròn tâm $O$, áp dụng công thức trung tuyến trong tam giác $ABM$:

 

$MO^2=\frac{MA^2+MB^2}{2} - \frac{AB^2}{4} \Rightarrow 4MO^2+AB^2=2(MA^2+MB^2) \geq (MA+MB)^2$

        $\Rightarrow P = MA+MB \leq \sqrt{4MO^2+AB^2}$ (không đổi)

 

Dấu "=" xảy ra khi và chỉ khi $M$ là giao của đường tròn tâm $O$ với đường trung trực đoạn $AB$.

 

Bài toán mở rộng của anh perfectstrong rất thú vị nhưng em chưa nghĩ ra, chúng ta cùng tiếp tục thảo luận nào.

Xét 3 TH sau:

 

TH1: $ x \geq 0$

 

Áp dụng bđt Cauchy có:

$VP=3.\sqrt[3]{x^2.x.(x+2)} \leq x^2+2x+2$

 

Lại có

$x^2+2x+2 < 2x^2+x+3 \Leftrightarrow x^2-x+1 >0$ (luôn đúng)

 

Vậy $VT>VP$

 

TH2: $-2<x<0$

 

Có $VT>0 >VP$

 

TH3: $x \leq -2$

 

Áp dụng bđt Cauchy có:

$VP=3.\sqrt[3]{x^2.(-x).(-x-2)} \leq x^2-2x-2$

 

Lại có

$x^2-2x-2 < 2x^2+x+3 \Leftrightarrow x^2+3x+5 >0$ (luôn đúng)

 

Vậy $VT>VP$

 

Tóm lại ta có $VT>VP$ với mọi số thực x nên pt vô nghiệm.

Phân tích:

 

Định hướng tách $\frac{2024}{a+b} = \frac{m}{a+b}+\frac{n}{a+b}$ rồi dùng Cauchy và còn biểu thức $a+b$ đi tìm GTLN hoặc GTNN.

 

Với giả thiết $a^2+4b=8$ ta có:

$4.(a+b)=4a+8-a^2=12-(a-2)^2 \leq 12 \Rightarrow a+b \leq 3$

Dấu "=" xảy ra khi và chỉ khi $a=2, b=1$

 

Khi đó ta sẽ có $(a+b)^2=9 \Rightarrow a+b=\frac{9}{a+b}$.

 

Như vậy có được lời giải như sau:

 

$P= (a+b)+\frac{9}{a+b}+\frac{2015}{a+b}$

 

Áp dụng bđt Cauchy, với $a, b$ không âm ta có:

$(a+b)+\frac{9}{a+b} \geq 6$

Dấu "=" xảy ra khi và chỉ khi $a+b=3$

 

Với giả thiết $a^2+4b=8$ và $a, b$ không âm ta có:

$4.(a+b)=4a+8-a^2=12-(a-2)^2 \leq 12 \Rightarrow a+b \leq 3 \Rightarrow \frac{2015}{a+b} \geq \frac{2015}{3}$

Dấu "=" xảy ra khi và chỉ khi $a=2, b=1$

 

Từ đó có $min P = \frac{2033}{3}$ tại $a=2, b=1$

Cho bàn cờ $4*4$.

Có bao nhiêu cách đặt các quân mã lên bàn cờ đó sao cho trên mỗi ô chứa nhiều nhất 1 quân mã, mỗi quân mã chỉ nằm trên 1 ô và mỗi hàng, mỗi cột chỉ chứa đúng 2 quân mã?

a, Tứ giác $MAOB$ có 2 góc $\widehat{OAM}, \widehat{OBM}$ đối nhau và là góc vuông nên tổng của chúng bằng $180^{o}$, do đó nội tiếp.

 

b, $\triangle MAD \sim \triangle MCA$ (g.g) nên ta có $\frac{MA}{MD}=\frac{MC}{MA}$ suy ra $MA^2=MC.MD$

 

c, Dễ thấy các tứ giác $ADBE, AMBO, AMDH$ nội tiếp nên ta có:

$\widehat{ADE}=\widehat{ABE}=\widehat{ABO}=\widehat{AMO}=\widehat{AMH}=\widehat{ADH}$ nên $D, H, E$ thẳng hàng.

 

Để ý rằng ta luôn có $\left[\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}\right] .\left[\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right]=4cx$

 

Do đó $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$

 

$\Leftrightarrow \begin{cases} \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a & \\ \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=2\frac{c}{a}.x& \end{cases} \Leftrightarrow \begin{cases} \sqrt{(x+c)^{2}+y^{2}} = a+ \frac{c}{a}x& \\ \sqrt{(x-c)^{2}+y^{2}}=a- \frac{c}{a}x &\end{cases} \Rightarrow \begin{cases}(x+c)^{2}+y^{2} =a^2+2cx+\frac{c^2}{a^2}x^2 & \\ (x-c)^{2}+y^{2} =a^2-2cx+\frac{c^2}{a^2}x^2 & \end{cases}$

 

$\Leftrightarrow x^2+c^2+y^2=a^2+\frac{c^2}{a^2}x^2 \Leftrightarrow \frac{a^2-c^2}{a^2}x^2+y^2=a^2-c^2 \Leftrightarrow \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1.$

 

Với chiều ngược lại ở vị trí dấu suy ra phía trên, ta có:

 

$\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \Rightarrow x^2 \leq a^2 \Leftrightarrow -a\leq x \leq a$

Do $0<c<a$ nên $-a^2<cx<a^2 \Leftrightarrow -a <\frac{c}{a}x<a$

Phá dấu giá trị tuyệt đối và ta được 2 phương trình tương đương nhau.

a,

Trước hết phân tích ra thừa số nguyên tố:

$23520=2^5*3*5*7^2$

Số cần tìm phải có số chữ số ít nhất có thể.

Từ phân tích trên có thể thấy, số cần tìm sẽ chứa đúng một chữ số $5$ và hai chữ số $7$.

Ta cần viết tích $2^5*3$ thành tích của ít chữ số nhất, cụ thể là ba chữ số. Có các cách viết sau:

$2^5*3=4*4*6$

$2^5*3=8*4*3$

$2^5*3=8*2*6$

Đến đây, chọn cách viết cuối sẽ lập được số nhỏ nhất, đó là $256778$.

 

b,

Do $990=2*3^2*5*11$ trong đó $11$ là số nguyên tố có hai chữ số nên đáp án là không tìm được.

 

c,

Tương tự câu a, có:

$2700=2^2*3^3*5^2$

Số cần tìm sẽ chứa đúng hai chữ số $5$.

Tích $2^2*3^3$ có thể viết thành tích của ít nhất ba chữ số như sau:

$2^2*3^3=4*3*9$

$2^2*3^3=2*6*9$

$2^2*3^3=6*6*3$

Chọn cách viết thứ hai, lập được số $25569$.

 

Câu hỏi mở rộng: thay số tự nhiên nhỏ nhất thành lớn nhất trong đề bài, đáp án sẽ là gì?

Đường tròn tâm $I$ luôn tiếp xúc hai tia $Ox, Oy$ nên $I$ di chuyển trên tia phân giác $Oz$ của góc $xOy$, trừ điểm $I$.

 

Gọi $M$ là chân đường vuông góc hạ từ $A$ xuống $Oz$ thì thấy $DF$ đi qua $M$, chính là điểm cố định cần tìm. Ta sẽ chứng minh $DF$ luôn đi qua $M$.

 

Xét lần lượt các vị trí của $I$ từ gần đến xa $O$:

 

TH1: $OI<OM, AE>AM$

4 điểm $A,E,I,F,M$ thuộc đường tròn đường kính $AI$.

Ta có $OI.OM=OE.OA=OD.OA \Rightarrow \frac{OD}{OM}=\frac{OI}{OA}$ nên $\bigtriangleup ODM \sim \bigtriangleup OIA$ $(c.g.c)$ $(1)$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{EAI}=\widehat{FAI}=\widehat{OMF}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH2: $OI<OM, AE=AM$ thì $F$ trùng $M$

 

 

TH3: $OI<OM, AE<AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{FAI}=\widehat{FMz}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH4: $I$ trùng $M$

Có $\widehat{AIE}=\widehat{AIF}, \widehat{EIO}=\widehat{DIO}$

Mà $\widehat{AIE}+\widehat{EIO}=\widehat{AIO}=90^{\circ}$

nên $\widehat{AIE}+\widehat{AIF}+\widehat{EIO}+\widehat{DIO}=180^{\circ}$ hay $F, I, D$ thẳng hàng.

Vậy $D, M, F$ thẳng hàng.

 

 

TH5: $OI>OM, OE<OA$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{FAI}=\widehat{FMI}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH6: $OI>OM, OE>OA, AE<AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI} \Rightarrow \widehat{IMD}=\widehat{EAI}=90^{\circ}-\widehat{EIA}=90^{\circ}-\widehat{FIA}=90^{\circ}-\widehat{FMA}$

$\Rightarrow \widehat{IMD}+\widehat{FMA}=90^{\circ}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH7: $OI>OM, AE=AM$ thì $F$ trùng $M$

 

 

TH8: $OI>OM, OE>OA, AE>AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI} \Rightarrow \widehat{IMD}=\widehat{EAI}=\widehat{FAI}=\widehat{EAI}=\widehat{IMF}$

Vậy $D, M, F$ thẳng hàng.

 

 

Kết thúc bài toán.

Ta có:

$P=(x+y+z)-\left ( \frac{xy^2}{x^2+y^2}+\frac{yz^2}{y^2+z^2}+\frac{zx^2}{z^2+x^2} \right )+\frac{1}{\sqrt{x+y+z}}$

 

Với $x, y, z$ là các số dương có:

$x^2+y^2 \geq 2xy \Rightarrow \frac{xy^2}{x^2+y^2} \leq \frac{y}{2}$

tương tự:

$\frac{yz^2}{y^2+z^2} \leq \frac{z}{2}, \frac{zx^2}{z^2+x^2} \leq \frac{x}{2}$

 

$\Rightarrow \frac{xy^2}{x^2+y^2}+\frac{yz^2}{y^2+z^2}+\frac{zx^2}{z^2+x^2} \leq \frac{x}{2}+\frac{y}{2}+\frac{z}{2}$

 

$\Rightarrow P \geq \frac{x+y+z}{2} + \frac{1}{\sqrt{x+y+z}},$ $(1)$

 

Dấu "=" xảy ra $\Leftrightarrow x=y=z.$

 

Tiếp tục có

$\frac{x+y+z}{2} + \frac{1}{\sqrt{x+y+z}} = \frac{x+y+z}{2} + \frac{1}{2\sqrt{x+y+z}} + \frac{1}{2\sqrt{x+y+z}}$

 

$\geq 3.\sqrt[3]{\frac{x+y+z}{2} . \frac{1}{2\sqrt{x+y+z}} . \frac{1}{2\sqrt{x+y+z}}}=\frac{3}{2}.$ $(2)$

 

Dấu "=" xảy ra $\Leftrightarrow \frac{x+y+z}{2} = \frac{1}{2\sqrt{x+y+z}} \Leftrightarrow x+y+z=1.$

 

Từ $(1)$ và $(2) \Rightarrow P \geq \frac{3}{2}$. Dấu "=" xảy ra $\Leftrightarrow x=y=z=\frac{1}{3}.$

 

Vậy $min P = \frac{3}{2}$ tại $x=y=z=\frac{1}{3}.$

Mình trình bày lời giải bằng hình học giải tích:

 

Đặt hệ trục $Oxy$ với $O$ trùng $A$, tia $Oy$ trùng tia $Ax$, tọa độ $B(50\sqrt{2}, 50\sqrt{2})$ (hình vẽ).

 

Sau $t$ giây, chất điểm $X$ nằm ở vị trí $M(0, 3\sqrt{2}t)$.

$\overrightarrow{BY}$ cùng hướng với $\vec{u}=(1, -1)$

Do $Y$ di chuyển trên tia $By$ từ $B$ với $v=4(cm/s)$ nên sau $t$ giây, chất điểm $Y$ nằm ở vị trí $N$ sao cho

$\overrightarrow{BN}=(2\sqrt{2}t, -2\sqrt{2}t)$

$\Leftrightarrow N (50\sqrt{2}+2\sqrt{2}t, 50\sqrt{2}-2\sqrt{2}t)$

 

Có $MN^2=(50\sqrt{2}+2\sqrt{2}t)^2+(50\sqrt{2}-5\sqrt{2}t)^2 = 58t^2-600t+10000.$

Đến đây xét hàm số với $t \geq 0$ được $min MN = \sqrt{\frac{245000}{29}}$(cm).

Trên mặt phẳng cho đường tròn tâm $O$, hai điểm $A$ và $B$ đối xứng nhau qua $O$ và nằm ngoài đường tròn $(O)$. Tìm vị trí các điểm $M$ trên đường tròn $(O)$ sao cho $P=MA+MB$ đạt GTLN, GTNN?

Em là học sinh THPT, mong muốn đưa ra lời giải bằng cách THPT để kết thúc mọi người có thể tham khảo, mong ad duyệt cho ạ!

Đặt $P=3x^2+2y^2$

 

Xét 2 TH sau:

TH1: $y = 0$

Ta có $x^2=5$ và $P=15$

 

TH2: $y\neq0$

Ta có $\frac{P}{5}=\frac{3x^2+2y^2}{x^2-y^2+2xy}=\frac{3t^2+2}{t^2+2t-1}$, với $t=\frac{x}{y}$

Do $y^2.(t^2+2t-1)=5$ nên $t^2+2t-1 >0$

 

Xét hàm số $f(t)=\frac{3t^2+2}{t^2+2t-1}, t \in (-\infty;-1-\sqrt{2})\cup (-1+\sqrt{2};+\infty)$

 

Có $f'(t)=\frac{6t^2-10t-4}{t^4+4t^3+2t^2-4t+1}$

$f'(t)=0 \Leftrightarrow t=2$

 

Lập bảng biến thiên và thu được $min f(t) = f(2) = 2$

Hệ $\left\{\begin{matrix} x=2y\\x^2-y^2+2xy=5 \end{matrix}\right.$ có nghiệm $(x; y)=\left ( \pm 2\frac{\sqrt{5}}{\sqrt{7}};\pm\frac{\sqrt{5}}{\sqrt{7}}\right)$

 

Kết luận: $min P = 10$

Cho 3 điểm $I, A, B$ với $A$ là trung điểm $BI$. Điểm $M$ trong mặt phẳng thỏa mãn $3MA=2MB$. Tính độ dài nhỏ nhất của đoạn $MI$ theo $AB$.

TH1: $2m-3 \geq 8 \Leftrightarrow m \geq \frac{11}{2}$

$A \cap B$ có đúng 5 số nguyên khi

$2 \leq 4-3m < 3 \Leftrightarrow \frac{1}{3} < m \leq \frac{2}{3}$, không thỏa điều kiện.

TH2: $4-3m <2m-3 < 8 \Leftrightarrow \frac{7}{5} <m<\frac{11}{2}$

$(2m-3)-(4-3m)=5m-7$

Khi đó $A \cap B= (4-3m;2m-3)$ có đúng 5 số nguyên thì điều kiện cần là

$4<5m-7 \leq 6 \Leftrightarrow \frac{11}{5}<m\leq \frac{13}{5}$

Với điều kiện trên, ta có $-3,8 \leq 4-3m<-2,6$ và $1,4<2m-3\leq 2,2$

$A \cap B$ có đúng 5 số nguyên khi xảy ra 1 trong 2 TH sau:

• TH1: $\left\{\begin{matrix} 4-3m<-3\\ 1<2m-3 \leq 2 \end{matrix}\right.\Leftrightarrow \frac{7}{3}<m\leq \frac{5}{2}.$
• TH2: $\left\{\begin{matrix} -3\leq 4-3m<-2\\ 2<2m-3 \end{matrix}\right.$    (vô nghiệm)

Kết hợp điều kiện có $m \in \left(\frac{7}{3}; \frac{5}{2}\right]$ thỏa mãn đề bài.