nguyenthanhhung1985's Content
There have been 85 items by nguyenthanhhung1985 (Search limited from 08-06-2020)
#684783 Cho đa thức $f(x)=x^3=3x^2+9x+1964$
 Posted by
nguyenthanhhung1985
on 17-06-2017 - 10:23
in
Đa thức
Posted by
nguyenthanhhung1985
on 17-06-2017 - 10:23
in
Đa thức
#684796 so sánh $\sqrt{7-\sqrt{4}+4\sqrt{5...
 Posted by
nguyenthanhhung1985
on 17-06-2017 - 13:15
in
Đại số
Posted by
nguyenthanhhung1985
on 17-06-2017 - 13:15
in
Đại số
$$\sqrt{7-\sqrt{4}+4\sqrt{5}}=\sqrt{5+4\sqrt{5}}=\sqrt{5-2\sqrt{5}+6\sqrt{5}}>\sqrt{5-2\sqrt{5}+1}=\sqrt{(\sqrt{5}-1)^2}=\sqrt{5}-1$$
#684843 $P=\frac{1}{2+6a^{2}+9a^{4}...
 Posted by
nguyenthanhhung1985
on 17-06-2017 - 22:08
in
Bất đẳng thức và cực trị
Posted by
nguyenthanhhung1985
on 17-06-2017 - 22:08
in
Bất đẳng thức và cực trị
Bạn có thể rút $b=2-a$ thế vào $$P=\dfrac{1}{2+6a^2+9a^4}+\dfrac{1}{2+6(2-a)^2+9(2-a)^4}$$
Tìm GTNN của hàm $$f(x)=\dfrac{1}{2+6x^2+9x^4}+\dfrac{1}{2+6(2-x)^2+9(2-x)^4}$$ trên $(0;2)$
Em tự tính đạo hàm, lập bảng biến thiên và quan sát bảng biến thiên kết luận.
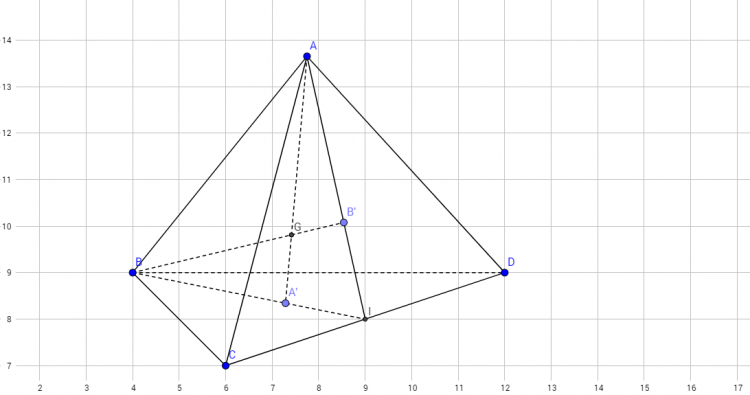
#684849 Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
 Posted by
nguyenthanhhung1985
on 17-06-2017 - 23:24
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 17-06-2017 - 23:24
in
Hình học không gian
Gọi M, N lần lượt trung điểm AB và CD (MN là đoạn vuông góc chung của AB, CD).
Ta thấy: tâm $I$ đường tròn ngoại tiếp tứ diện nằm trên MN sao cho $\dfrac{MI}{NI}=\frac{7}{2}$
Suy ra: $IA=IB=IC=ID$ (Giờ ta tính bán kính)
Xét tam giác AMC: $MC=\sqrt{22a^2-4a^2}=3\sqrt{2}a$
Xét tam giác AMD: $MD=\sqrt{22a^2-4a^2}=3\sqrt{2}a$
Xét tam giác MCN: $MN=\sqrt{18a^2-9a^2}=3a$
Do: $\dfrac{MI}{NI}=\frac{7}{2}$ nên $MI=\dfrac{7a}{3}$ và $NI=\dfrac{2a}{3}$
Xét tam giác AMI: $IA=\sqrt{\dfrac{49a^2}{9}+4a^2}=\dfrac{\sqrt{85}a}{3}$
Vậy bán kính mặt cầ ngoại tiếp tứ diện: $R=\dfrac{\sqrt{85}a}{3}$
Các bạn kiểm tra iaij giúp mình kết quả...
#684865 tìm x $x+\sqrt{x}-2=2\sqrt{x-1}$
 Posted by
nguyenthanhhung1985
on 18-06-2017 - 09:34
in
Đại số
Posted by
nguyenthanhhung1985
on 18-06-2017 - 09:34
in
Đại số
Hình như mình thấy nghiệm của phương trình bậc 3 của bạn không là nghiệm của phương trình trên. Bạn thử kiểm tra lại xem.
#684867 tìm x $x+\sqrt{x}-2=2\sqrt{x-1}$
 Posted by
nguyenthanhhung1985
on 18-06-2017 - 09:38
in
Đại số
Posted by
nguyenthanhhung1985
on 18-06-2017 - 09:38
in
Đại số
Mình nghĩ:
Điều kiện: $x\ge 1$
Phương trình được viết lai:
$(x-1)+(\sqrt{x}-1)-2\sqrt{x-1}=0
Nhân thêm lượng liên hiệp, rồi nhốm nhân tử chung.
Cứ giải như thế, mình đi có việc tí.
#685119 Phương pháp liên hợp với phương trình chỉ có 1 nghiệm vô tỷ
 Posted by
nguyenthanhhung1985
on 20-06-2017 - 10:51
in
Chuyên đề toán THCS
Posted by
nguyenthanhhung1985
on 20-06-2017 - 10:51
in
Chuyên đề toán THCS
Đề của bạn có vấn đề: Giải phương trình sau:
$$\sqrt[3]{x^2-1}+x=\sqrt{x^3-2}$$
Cách giải:
Điều kiện:$x\ge \sqrt[3]{2}$.
Phương trình đã cho tương đương:
$$(\sqrt[3]{x^2-1}-2)+x-3=\sqrt{x^3-2}-5$$
$$\iff (x-3)+\dfrac{x^2-9}{\sqrt[3]{(x^2-1)^2+2\sqrt[3]{x^2-1}+4}}=\dfrac{(x-3)(x^2+3x+9)}{\sqrt{x^3-2}+5}$$
$$\iff (x-3)(1+\dfrac{x+3}{\sqrt[3]{(x^2-1)^2+2\sqrt[3]{x^2-1}+4}-\dfrac{x^2+3x+9}{\sqrt{x^3-2}+5})$$
$$\iff x=3$$ hoặc $$1+\dfrac{x+3}{\sqrt[3]{(x^2-1)^2+2\sqrt[3]{x^2-1}+4}=\dfrac{x^2+3x+9}{\sqrt{x^3-2}+5}$$(*)
Ta chứng minh (*) vô nghiêm.
Chứng minh VP: $$\dfrac{x^2+3x+9}{\sqrt{x^3-2}+5}>2$$
Chứng minh VT:$$1+\dfrac{x+3}{\sqrt[3]{(x^2-1)^2+2\sqrt[3]{x^2-1}+4}<2$$
Nên phương trình (*) vô nghiệm.
Vậy phương trình có 1 nghiệm $x=3$
#685124 Tính $P=2sina-3cosa$ biết $cota=-0.75$ và $\fra...
 Posted by
nguyenthanhhung1985
on 20-06-2017 - 11:23
in
Công thức lượng giác, hàm số lượng giác
Posted by
nguyenthanhhung1985
on 20-06-2017 - 11:23
in
Công thức lượng giác, hàm số lượng giác
Nhận xét: Do $\dfrac{\pi}{2}<a<\pi$ và cho $\cot(a)=-0,75$ nên ta đi tính $\sin(a)$ và $\cos(a)$ rồi thế vào $P$ là xong.
Sử dụng công thức: $\cot^2(a)+1=\dfrac{1}{\sin^2(a)}$
$\iff \sin(a)=\pm \sqrt{\dfrac{1}{\cot^2(a)+1}}$
$\iff \sin(a)=\pm \dfrac{4}{5} $
$Do \dfrac{\pi}{2}<a<\pi$ nên $\sin(a)=\dfrac{4}{5}$
Sử dụng công thức: $\sin^2(a)+\cos^2(a)=1 \iff \cos(a)=\pm \sqrt{1-\sin^2(a)}=\pm \dfrac{3}{5}$
$Do \dfrac{\pi}{2}<a<\pi$ nên $\cos(a)=-\dfrac{3}{5}$
Thế vào $P$ ta được: $P=\dfrac{17}{5}$
#685131 Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
 Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:13
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:13
in
Hình học không gian
Chung ta biết $MN$ đã lấy như trên nên tâm mặt cầu sẽ nằm trên $MN$. Tới đây ta có một cách làm như sau.
Gọi $I$ là tâm của mặt cầu trên.
Khi đó ta có:
$$IA^2=ID^2$$
$$\iff IM^2+MA^2=IN^2+ND^2$$
$$\iff IM^2+IA^2=(3a-IM)^2+ND^2$$
$$\iff IM^2+4a^2=9a^2-6aIM+IM^2+9a^2$$
$$\iff 6aIM=14a^2 \iff IM=\dfrac{7a}{3}$$
Và $IN=\dfrac{2a}{3}$
Từ đó ta có tỉ số trên nhen bạn...
#685135 $y=\log_{\sqrt{2}} \left ( \frac{x+1}{3-2x} \ri...
 Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:35
in
Phương trình - hệ phương trình - bất phương trình
Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:35
in
Phương trình - hệ phương trình - bất phương trình
a) Điều kiện: $\dfrac{x+1}{3-2x}>0 \iff (x+1)(3-2x)>0 \iff -2x^2+x+3>0 \iff -1<x< \dfrac{3}{2}$
Vậy: $D=(-1;\dfrac{3}{2})
#685136 Tìm số cực trị
 Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:40
in
Hàm số - Đạo hàm
Posted by
nguyenthanhhung1985
on 20-06-2017 - 12:40
in
Hàm số - Đạo hàm
có 2 cực trị. B
#685212 tính A= tan$9^{\circ} - tan127^{\circ} - t...
 Posted by
nguyenthanhhung1985
on 21-06-2017 - 00:27
in
Các bài toán Lượng giác khác
Posted by
nguyenthanhhung1985
on 21-06-2017 - 00:27
in
Các bài toán Lượng giác khác
Tính
$$A=\tan(9^0)-\tan(27^0)-\tan(63^0)+\tan(81^0)$$
$$=\tan(9^0)-\tan(27^0)-\cot(27^0)+\cot(9^0)$$
$$=\dfrac{2}{\sin(18^0)}-\dfrac{2}{\sin(54^0)}$$
$$=\dfrac{2}{\sin(18^0)}-\dfrac{2}{\sin(3.18^0)}$$
$$=\dfrac{2}{\sin(18^0)}-\dfrac{2}{3\sin(18^0)-4\sin^3(18^0)}$$
Do: $\sin(18^0)=\dfrac{\sqrt{5}-1}{4}$ (Đặt: $18^0=x$, $\sin(2x)=\sin(3x)$ nên ta có phương trình $4sin^2(x)+2\sin(x)-1=0$ giải ta được $\sin(x)$)
Thế vào $A$ ta được: $A=4$
#685214 $sin^{\frac{x}{2}}+sinx-2cos^{\frac{x}{2}}=\frac{1}{2}$
 Posted by
nguyenthanhhung1985
on 21-06-2017 - 06:39
in
Phương trình, Hệ phương trình Lượng giác
Posted by
nguyenthanhhung1985
on 21-06-2017 - 06:39
in
Phương trình, Hệ phương trình Lượng giác
#685320 $\lim_{x\rightarrow 0}\frac{\sqrt...
 Posted by
nguyenthanhhung1985
on 21-06-2017 - 22:52
in
Dãy số - Giới hạn
Posted by
nguyenthanhhung1985
on 21-06-2017 - 22:52
in
Dãy số - Giới hạn
#685321 Tìm giới hạn $\lim_{x\to 4} {\frac{4...
 Posted by
nguyenthanhhung1985
on 21-06-2017 - 23:06
in
Dãy số - Giới hạn
Posted by
nguyenthanhhung1985
on 21-06-2017 - 23:06
in
Dãy số - Giới hạn
#685324 Chứng minh: $8sin^{3}18^{o}+8sin^{2}18^...
 Posted by
nguyenthanhhung1985
on 22-06-2017 - 05:38
in
Công thức lượng giác, hàm số lượng giác
Posted by
nguyenthanhhung1985
on 22-06-2017 - 05:38
in
Công thức lượng giác, hàm số lượng giác
sau đó chúng ta thế vaof vế trái thì ta được điều phải chứng minh.
#685443 $16sin^{6}x-32sin^{4}x+21sin^{2}x-5=0$
 Posted by
nguyenthanhhung1985
on 24-06-2017 - 05:56
in
Phương trình, Hệ phương trình Lượng giác
Posted by
nguyenthanhhung1985
on 24-06-2017 - 05:56
in
Phương trình, Hệ phương trình Lượng giác
phương trình tương đương: $16t^3-32t^2+21t-5=0$
$\iff (t-1)(16t^2-16t+5)=0$
$\iff t=1 or 16t^2-16t+5=0$
$\iff t=1$ pt sau vô nghiệm.
$\iff \sin^2(x)=1$
$\iff \sin(x)=1 or \sin(x)=-1$
$\iff x=\frac{\pi}{2}+2k\pi or x=-\frac{\pi}{2}+2k\pi$
#685530 Phương trình lượng giác
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 10:04
in
Phương trình, Hệ phương trình Lượng giác
Posted by
nguyenthanhhung1985
on 25-06-2017 - 10:04
in
Phương trình, Hệ phương trình Lượng giác
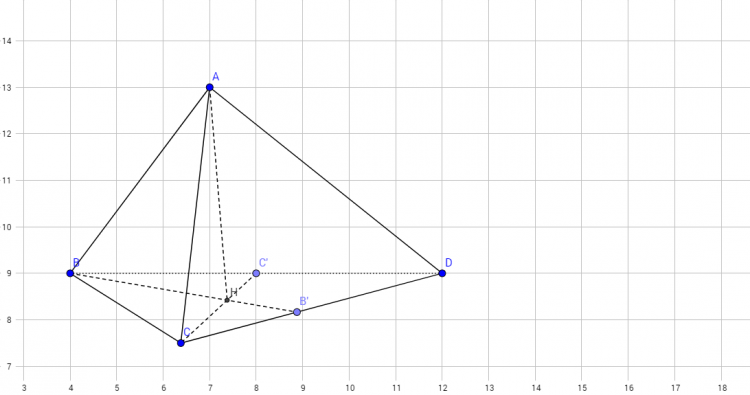
#685560 Cho tứ diện $ABCD$ biết $AB = CD = a,\,\,AD = BC = b...
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 17:48
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 25-06-2017 - 17:48
in
Hình học không gian
Nhận xét: Tứ diện có $AB=CD=a; AC=BD=b; BC=AD=c$ nên tứ diện $ABCD$ là tứ diện gần đều
Bước 1: Dựng thiết diện vuông $AB'C'D'$ như sau: Trong mặt phẳng $(BCD)$ các đường thẳng qua $B$ song song $CD$, qua $C$ song song với $BD$ và qua $D$ song song với $BC$ tạ
o thành tam giác $B'C'D'$
Ta cần chứng minh: Tứ giác $AB'C'D'$ là tứ diện vuông (Hay đôi một vuông góc tại $A$)
*Từ cách dựng ta suy ra: $DB'=DC'=BC=c$
*Do giả thiết: $BC=AD'$
*Suy ra: $DA=DB'=DC'$
*Cho nên tam giác AB'C' là tam giác vuông tại A
*Tương tự như vậy các tam giác AC'D' và AB'D'
Bước 2: Tính $V_{A.B'C'D'}$ rồi tính $V_{A.BCD}$
*Theo định lý Pi-ta-go áp dụng vào các tam giác vuông đã được ở trên ta có:
$B'C'^2=AB'^2+AC'^2=4c^2$ (1)
$B'D'^2=AB'^2+AD'^2=4b^2$ (2)
$C'D'^2=AD'^2+AC'^2=4a^2$ (3)
Cộng (1) (2) (3) theo từng vế ta có:
$AB'^2+AC'^2+AD'^2=2(a^2+b^2+c^2)$ (4)
Lấy (4) trừ (3), trừ (2) và trừ (1) ta được:
$AB'=\sqrt{2}\sqrt{b^2+c^2-a^2}$
$AC'=\sqrt{2}\sqrt{a^2+c^2-b^2}$
$AD'=\sqrt{2}\sqrt{a^2+b^2-c^2}$
Suy ra: $V_{A.B'C'D'}=\dfrac{AB'.AC'.AD'}{6}=\dfrac{\sqrt{2}}{3}\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}$
*Hai hình chóp A.BCD và A.B'C'D' có cùng đường cao nhưng:
$S_{BCD}=\dfrac{1}{4}S_{B'C'D'}$
Nên suy ra thể tích của hình chóp A.BCD là:
$V_{ABCD}=\dfrac{\sqrt{2}}{12}\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}$
Bước 3: Kết luận
#685564 Tìm bán kính của mặt cầu ngoại tiếp tứ diện(Hình chóp)
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 18:21
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 25-06-2017 - 18:21
in
Hình học không gian
Bài 1: Cho tứ diện $OABC$ vuông tại $A$ (có $OA\bot OB \text{và} OB\bot OC, OC\bot OA$ ) với $OA=a; OB=b; OC=c$
a) Tính bán kính của mặt cầu ngoại tiếp tứ diện $OABC$
b) Tính bán kính của mặt cầu nội tiếp tứ diện $OABC$
Bài 2: Cho tứ diện $ABCD$ với : $AB=CD=a; AC=BD=b; AD=BC=c$.
a) Tính bán kính của mặt cầu ngoại tiếp tứ diện $ABCD$
b) Tính bán kính của mặt cầu nội tiếp tứ diện $ABCD$
#685567 HÌNH TRỤ NỘI TIẾP HÌNH CẦU
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 18:32
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 25-06-2017 - 18:32
in
Hình học không gian
Một hình trụ được gọi là nội tiếp trong một hình cầu nếu hai đường tròn đáy của hình trụ nằm trên mặt cầu.
a) Tính thể tích hình trụ nội tiếp trong hình cầu bán kính R nếu bết chiều cao h của nó.
b) Tính thể tích lớn nhất của hình trụ nói trên hi h thay đổi.
#685568 Ôn Tổng Hợp
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 19:02
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 25-06-2017 - 19:02
in
Hình học không gian
Câu a) Tính thể tích khối chóp S.ABCD
Theo giả thiết ta có:
*Tứ giác ABCD là hình vuông nên $AC=a\sqrt{2}$ suy ra: $OA=\dfrac{AC}{2}=\frac{a\sqrt{2}}{2}$
*Tam giác SOA vuông tại O nên $OS=\sqrt{OA^2-OA^2}=\frac{a\sqrt{14}}{2}$
Diện tích hình vuông cạnh a: $S_ABCD=a^2$
Thể tích khối chóp S.ABCD: $V_S.ABCD=\frac{1}{3}S_ABCD.SO=\frac{a^3\sqrt{14}}{6}$
#685571 Ôn Tổng Hợp
 Posted by
nguyenthanhhung1985
on 25-06-2017 - 19:17
in
Hình học không gian
Posted by
nguyenthanhhung1985
on 25-06-2017 - 19:17
in
Hình học không gian
Câu b) Gọi I là trung điểm CD. Dựng OK vuông góc SI tại K.
Do: $OK \bot CD$ và $OK \bot SI$ nên $OK \bot (SCD)$
Suy ra: $d(O, (SCD))=OK=?$
Xét tam giác OIS vuông tại O: $\frac{1}{OK^2}=\frac{1}{OI^2}+\frac{1}{OS^2}=\frac{4}{a^2}+\frac{2}{7a^2}=\frac{30}{7a^2}$
Suy ra OK=? là xong
#685610 PHÂN LOẠI CÁC TỨ DIỆN TRONG KHÔNG GIAN
 Posted by
nguyenthanhhung1985
on 26-06-2017 - 10:26
in
Chuyên đề toán THPT
Posted by
nguyenthanhhung1985
on 26-06-2017 - 10:26
in
Chuyên đề toán THPT
PHÂN LOẠI CÁC TỨ DIỆN TRONG KHÔNG GIAN
I.TỨ DIỆN
1. Kiến thức cơ bản
$\bullet$Tứ diện là hình có bốn mặt.
2. Một số bài toán cơ bản
Bài 1. Cho tứ diện $ABCD$, $G$ là trọng tâm tứ diện. Chứng minh rằng: các tứ diện $BGCD$, $GCDA$, $GDAB$ và $GABC$ có cùng thể tích?
Bài giải:
Gọi $h_A$, $H'_A$ là các khoảng cách hạ từ $A$ và $G$ xuống $(BCD)$. Ta có:
$\frac{V_{GBCD}}{V}=\frac{h'_A}{h_A}=\frac{GA'}{AA'}=\frac{1}{4} \Rightarrow V_{GBCD}=\frac{1}{4}V$
(Trong đó V là thể tích tứ diện $ABCD$)
Tương tự như vậy cho ba tứ diện nhỏ còn lại:
$V_{GBCD}=V_{GCDA}=V_{GDAB}=V_{GABC}=\frac{1}{4}V$
Bài 2. Cho tứ diện $ABCD$. Gọi $IJ$ là đoạn vuông góc chung của cặp cạnh đối $AB$ và $CD$ ($I$ thuộc $AB$, $J$ thuộc $CD$) và $\alpha$ là góc của cặp cạnh đó. Chứng minh thể tích của tứ diện được tính theo công thức: $V=\frac{1}{6}AB.CD.IJ.\sin(\alpha)$
Bài giải:
Ta dựng hình hộp "ngoại tiếp" tứ diện $ABCD$ như hình vẽ. Đặt:
$B=S_{AC_1BD_1}$
$h$ là chiều cao của hình hộp.
$h$ chính là độ dài của $IJ$ và $IJ \bot AB$ và $IJ \bot CD$
$\alpha$ là góc của $AB$ và $C_1D_1$
Ta có thể tích của hình hộp là:
$B.h=V_{C.ACBC_1}+V_{D.ABD_1}+V_{A.A_1CD}+V_{B.B_1CD}+V_{A.BCD}$
Nhưng $S_{ABC_1}=S_{ABD_1}=S_{A_1CD}=S_{B_1CD}=\frac{1}{2}$
Nên: $V_{C.ABC_1}=V_{D.ABD_1}=V_{A.A_1CD}=V_{B.B_1CD}=\frac{1}{6}B.h$
Suy ra: $V=V_{ABCD}=B.h-\frac{4}{6}B.h=\frac{1}{3}B.h$
Mặt khác: $IJ=h\,\, \text{và}\,\, B=\frac{1}{2}AB.C_1D_1.\sin(\alpha)=\frac{1}{2}AB.CD.\sin(\alpha)$
Cho nên cuối cùng ta có: $V=\frac{1}{6}AB.CD.IJ.\sin(\alpha)$
II.TỨ DIỆN VUÔNG
1. Kiến thức cơ bản:
$\bullet$Tứ diên vuông $O.ABC$, vuông tại $O$ là tứ diện có ba mặt $OAB$, $OBC$, $OAC$ là ba tam giác vuông.
$\bullet$Trong tứ diện vuông thì các cặp cạnh đối vuông góc với nhau từng đôi một
$\bullet$Công thức thể tích của tứ diện vuông: $V=\frac{1}{6}OA.OB.OC$
2. Một số bài toán cơ bản
Bài 1. Cho tứ diên vuông $OABC$ vuông tại $O$. Gọi $H, G$ lần lượt là trực tâm, trọng tâm của tam giác $ABC$. Tính $OH$, $OG$ theo $OA=a$, $OB=b$, $OC=c$.
Bài giải:
$\bullet$Gọi $CC'$ là đường cao xuất phát từ $C$ trong $(ABC)$. Định lý ba đường vuông góc cho $OC' \bot AB$. Ngoài ra ta biết rằng:
$$OH \bot (ABC)\implies OH \bot CC'$$
Ta có:
$\frac{1}{OH^2}=\frac{1}{OC^2}+\frac{1}{OC'^2}=\frac{1}{OA^2}+\frac{1}{OB^2}+\frac{1}{OC^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$
Suy ra: $OH=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}$
$\bullet$Do $G$ là trọng tâm của tam giác $ABC$ nên ta có:
$\vec{OG}=\frac{1}{3}(\vec{OA}+\vec{OB}+\vec{OC})$
Do đó:
$OG^2=\vec{OG}^2=\frac{1}{9}(OA^2+OB^2+OC^2)$
Vì:
$\vec{OA}.\vec{OB}=\vec{OB}.\vec{OC}=\vec{OC}.\vec{OA}=0$
Suy ra:
$OG=\frac{1}{3}\sqrt{a^2+b^2+c^2}$
Vậy:
$OH=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}$
$OG=\frac{1}{3}\sqrt{a^2+b^2+c^2}$
Bài 2. Cho tứ diện $O.ABC$ vuông tại $O$. Gọi $S$, $S_1$, $S_2$, $S_3$ lần lượt là diện tích các tam giác $ABC$, $OBC$, $OCA$, $OAB$. Chứng minh: $S^2=S_1^2+S_2^2+S_3^2$.
Bài giải:
Ta có:
$S_1^2+S_2^2+S_3^2=\frac{1}{4}OB^2.OC^2+\frac{1}{4}OC^2.OA^2+\frac{1}{4}OA^2.OB^2$
$=\frac{1}{4}OC^2(OA^2+OB^2)+\frac{1}{4}OA^2.OB^2$
$=\frac{1}{4}OC^2.AB^2+\frac{1}{4}OC'^2.AB^2$
$=\frac{1}{4}AB^2.(OC^2+OC'^2)$
$=\frac{1}{4}AB^2.CC'^2$
$=\frac{1}{2}AB^2.CC'^2$
$=S^2$ (đpcm)
Bài 3. Cho tứ diện $OABC$ vuông tại $O$ với $OA=a$, $OB=b$, $OC=c$. Tính thể tích tứ diện $OABC$.
Bài giải:
Thể tích của tứ diện
$V_{ABCD}=\frac{1}{6}OA.OB.OC=\frac{abc}{6}$
Bài 4. Cho tứ diện $OABC$ vuông tại $O$ với $OA=a$, $OB=b$, $OC=c$. Tính bán kính mặt cầu ngoại tiếp tứ diện $OABC$.
Bài giải:
$\bullet$Tam giác $AOB$ vuông tại $O$ nên tâm $I$ của đường tròn ngoại tiếp của nó là trung điểm của đoạn $AB$. Trục của đường tròn này là đường thẳng $Ix$ đi qua $I$ song song $OC$.
Trong mặt phẳng $(OC, Ix)$ vẽ đường trung trực của $OC$. Đường trung trực này cắt $Ix$ tại $K$, đó chính là tâm mặt cầu ngoại tiếp tứ diện $OABC$.
$\bullet$Tính bán kính $R$ của mặt cầu này là tính $R=OK$. Ta có:
$R^2=OK^2=OI^2+IK^2$
$\,\,\,=\frac{AB^2}{4}+\frac{OC^2}{4}$
$\,\,\,=\frac{OA^2+OB^2+OC}{4}$
$\,\,\,=\frac{a^2+b^2+c^2}{4}$
Vậy: $R=\frac{1}{2}\sqrt{a^2+b^2+c^2}$
Bài 5. Cho tứ diện $OABC$ vuông tại $O$ với $OA=a$, $OB=b$, $OC=c$. Tính bán kính mặt cầu nội tiếp tứ diện $OABC$.
Bài giải:
Bán kính của mặt cầu nội tiếp tính bởi: $r=\frac{3V}{S_{TP}}$
Trong đó các chi tiết được tính như sau:
$V=\frac{1}{6}OA.OB.OC=\frac{1}{6}abc$
$S_{TP}=S_{OAB}+S_{OBC}+S_{OAC}+S_{ABC}$
$\,\,\,\,=\frac{1}{2}ab+\frac{1}{2}bc+\frac{1}{2}ca+\frac{1}{2}AB.CA'$
Với $AB=\sqrt{a^2+b^2} \,\, \text{và} \,\, CA'^2=OA'^2+OC^2=\frac{a^2b^2+b^2c^2+c^2a^2}{a^2+b^2}$
$CA'=\frac{\sqrt{a^2b^2+b^2c^2+c^2a^2}}{\sqrt{a^2+b^2}}$
$S_{TP}=\frac{1}{2}(ab+bc+ca+\sqrt{a^2b^2+b^2c^2+c^2a^2})$
Vậy: $r=\frac{abc}{ab+bc+ca+\sqrt{a^2b^2+b^2c^2+c^2a^2}}$
III.TỨ DIỆN TRỰC TÂM(TỨ DIỆN TRỰC GIAO)
1. Kiến thức cơ bản:
$\bullet$Tứ diên trực tâm (hay là tứ diện trực giao) là tứ diện các cặp cạnh đối vuông góc nhau từng đôi một.
$\bullet$Tứ diện vuông, tứ diện đều là trường hợp đặc biệt của tứ diện trực tâm.
2. Một số bài toán cơ bản
Bài 1. Chứng minh rằng: Trong một tứ diện nếu có 2 cặp cạnh đối vuông góc nhau thì cặp cạnh đối thứ 3 cũng vuông góc nhau.
Bài giải:
Theo giả thiết $ABCD$ là tứ diện trực tâm nên $AB \bot CD$ và $AC \bot BD$
Vẽ $AH \bot (BCD)$. Ta có:
$CD \bot AB \,\, \text{và}\,\, CD \bot AH \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH$
$BD \bot AC \,\, \text{và}\,\, BD \bot AH \Rightarrow BD \bot (CAH) \Rightarrow BD \bot CH$
Hai kết quả trên cho ta thấy $H$ là trực tâm của tam giác $BCD$ nên ta có:
$BC \bot DH \,\, \text{và}\,\, BC \bot AH \Rightarrow BC \bot (ADH) \Rightarrow BC \bot AD$
Bài 2. Chứng minh một tứ diện trực tâm nếu và chỉ nếu tổng bình phương các cặp cạnh đối bằng nhau từng đôi một.
Bài giải:
$\bullet$ Thuận:
Cho tứ diện $ABCD$ có các cặp cạnh đối vuông góc nhau. Vẽ $BI \bot CD$ trong $BCD$. Ta có:
$CD \bot AB \,\, \text{và}\,\, CD \bot BI \Rightarrow CD \bot (ABI) \Rightarrow CD \bot AI$
Gọi $M$ là trung điểm $CD$. Ta có:
$AC^2-AD^2=2\overline{CD}.\overline{MI}$
$BC^2-BD^2=2\overline{CD}.\overline{MI}$
Suy ra:
$AC^2-AD^2=BC^2-BD^2 \iff AC^2+BD^2=BC^2+AD^2$ (1)
Nếu ta sử dụng thêm $BC \bot AD$ ta sẽ được:
$AB^2+CD^2=AC^2+BD^2$ (2)
Từ (1) và (2) ta được:
$AC^2+BD^2=BC^2+AD^2=AB^2+CD^2$ (3)
$\bullet$ Đảo:
Cho tứ diện $ABCD$ có các cạnh thỏa mãn (3). Ta chứng minh đó là một tứ diện trực tâm.
Vẽ đường cao $BI$ trong tam giác $BCD$, đường cao $AJ$ trong tam giác $ACD$. Vẫn gọi $M$ là trung điểm $CD$. Ta có:
$BC^2-BD^2=2\overline{CD}.\overline{MI}$ (4)
$AC^2-AD^2=2\overline{CD}.\overline{MJ}$ (5)
Từ (3) suy ra:
$BC^2-BD^2=AC^2-AD^2$
Do đó (4) và (5) cho ta: $I \equiv J$
Vậy: $CD \bot (ABI) \Rightarrow CD \bot AB$
Tương tự như vậy nếu ta sử dụng thêm cho hết giả thiết (3) ta sẽ được $BC \bot AD$ và $AC \bot BD$
IV. TỨ DIỆN GẦN ĐỀU
1. Kiến thức cơ bản:
$\bullet$Tứ diên gần đều(hoặc giả đều) là tứ diện có các cạnh đối bằng nhau từng đôi một. Do đó bốn mặt của nó là bốn tam giác bằng nhau và ngược lại.
$\bullet$Ta sẽ thấy có những điều kiện ít hơn dẫn tới tứ diện gần đều.
2. Một số bài toán cơ bản
Bài 1. Cho tứ diện vuông $OABC$ vuông tại $O$. Gọi $M$, $N$, $P$ lần lượt là trung điểm của $AB$, $BC$, $CA$. Chứng minh: $OMNP$ là một tứ diện gần đều.
Bài giải:
Tam giác $OAB$ vuông tại $O$: $OM=\frac{1}{2}AB$
Tam giác $CAB$ có đường trung bình là $PN$: $PN=\frac{1}{2}AB$
Cho nên: $OM=PN$
Tương tự như vậy ta cũng có: $ON=PM$ và $OP=MN$
Các cặp cạnh đối của tứ diện $OMNP$ bằng nhau từng đôi một nên tứ diện $OMNP$ là tứ diện gần đều.
Bài 2. Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Chứng tỏ rằng: $ACB'D'$ là tứ diện gần đều.
Bài giải:
Hai hình chữ nhật $ABCD$ và $A'B'C'D'$ bằng nhau nên: $AC=B'D'$
Tương tự ta cũng có: $AB'=CD'$ và $AD'=CB'$
Các cạnh đối của tứ diện $ACB'D'$ bằng nhau từng đôi một nên tứ diện $ACB'D'$ là tứ diện gần đều.
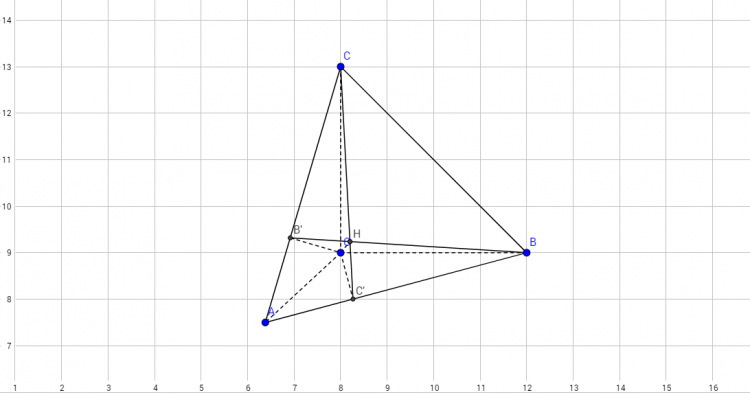
Bài 3. Cho tứ diện $ABCD$ có $AB=CD=a$, $AD=BC=b$, $AC=BD=c$. Tính thể tích tứ diện $ABCD$ theo $a,\,\,b,\,\,c$
Bài giải:
$\bullet$ Dựng thiết diện vuông $AB'C'D'$ như sau: Trong mặt phẳng $(BCD)$ các đường thẳng qua $B$ song song $CD$, qua $C$ song song với $BD$ và qua $D$ song song với $BC$ tạ
o thành tam giác $B'C'D'$
Ta cần chứng minh: Tứ giác $AB'C'D'$ là tứ diện vuông (Hay đôi một vuông góc tại $A$)
*Từ cách dựng ta suy ra: $DB'=DC'=BC=c$
*Do giả thiết: $BC=AD'$
*Suy ra: $DA=DB'=DC'$
*Cho nên tam giác AB'C' là tam giác vuông tại A
*Tương tự như vậy các tam giác AC'D' và AB'D'
$\bullet$ Tính $V_{A.B'C'D'}$ rồi tính $V_{A.BCD}$
*Theo định lý Pi-ta-go áp dụng vào các tam giác vuông đã được ở trên ta có:
$B'C'^2=AB'^2+AC'^2=4c^2$ (1)
$B'D'^2=AB'^2+AD'^2=4b^2$ (2)
$C'D'^2=AD'^2+AC'^2=4a^2$ (3)
Cộng (1) (2) (3) theo từng vế ta có:
$AB'^2+AC'^2+AD'^2=2(a^2+b^2+c^2)$ (4)
Lấy (4) trừ (3), trừ (2) và trừ (1) ta được:
$AB'=\sqrt{2}\sqrt{b^2+c^2-a^2}$
$AC'=\sqrt{2}\sqrt{a^2+c^2-b^2}$
$AD'=\sqrt{2}\sqrt{a^2+b^2-c^2}$
Suy ra: $V_{A.B'C'D'}=\dfrac{AB'.AC'.AD'}{6}=\dfrac{\sqrt{2}}{3}\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}$
*Hai hình chóp A.BCD và A.B'C'D' có cùng đường cao nhưng:
$S_{BCD}=\dfrac{1}{4}S_{B'C'D'}$
Nên suy ra thể tích của hình chóp A.BCD là:
$V_{ABCD}=\dfrac{\sqrt{2}}{12}\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}$
$\bullet$ Kết luận
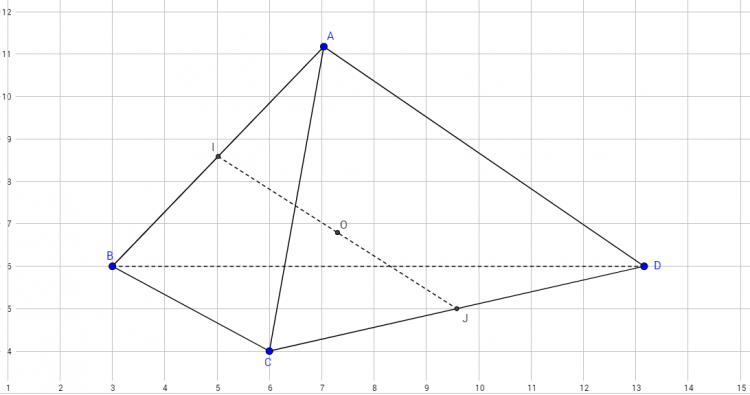
Bài 4. Cho tứ diện gần đều $ABCD$ với $AB=CD=a$; $AC=BD=b$, $AD=BC=c$. Tính bán kính mặt cầu ngoại tiếp tứ diên $ABCD$?
Bài giải:
$\bullet$ Gọi $I$, $J$ lần lượt là trung điểm của $AB$ và $CD$. Ta đã biết $IJ$ đoạn vuông góc chung của $AB$ và $CD$. Gọi $O$ là trung điểm của $IJ$. $O$ chính là tâm của mặt cầu ngoại tiếp tứ diện $ABCD$.
Thật vậy: $IJ$ là trung trực của $AB$ và $CD$ nên $OA=OB$ và $OC=OD$
Nhưng các đoạn nối trung điểm của các cạnh đối trong tứ diện đồng qui tại $O$ nên, chẳng hạn xét cặp $AC$ và $BD$ ta suy ra: $OA=OC$ và $OB=OD$
Vậy: $OA=OB=OC=OD$
$\bullet$ $\Delta ABC$ có trung tuyến $CI$ nên:
$CI^2=\frac{2CA^2+2CB^2-AB^2}{4}=\frac{2b^2+2c^2-a^2}{4}$
$\Delta IJC$ vuông tại $I$ nên:
$IJ^2=CI^2-CJ^2=\frac{2b^2+2c^2-a^2}{4}-\frac{a^2}{4}=\frac{b^2+c^2-a^2}{2}$
$\Delta AIO$ vuông tại $I$ nên:
$R^2=OA^2=AI^2+OI^2=\frac{AB^2}{4}+\frac{IJ^2}{4}=\frac{a^2+b^2+c^2}{8}$
$\iff R=\sqrt{\frac{a^2+b^2+c^2}{8}}$
Bài 5. Cho tứ diện gần đều $ABCD$ với $AB=CD=a$; $AC=BD=b$, $AD=BC=c$. Tính bán kính mặt cầu nội tiếp tứ diên $ABCD$?
Bài giải:
Bán kính mặt cầu nội tiếp tính bởi: $r=\frac{3V}{S_{TP}}$
Trong đó: $V_{ABCD}=\dfrac{\sqrt{2}}{12}\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}$
$S_{TP}=4\sqrt{p(p-a)(p-b)(p-c)}$ với $p=\frac{a+b+c}{2}$
Vậy: $r=\frac{\sqrt{2}}{16}.\frac{\sqrt{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}}{\sqrt{p(p-a)(p-b)(p-c)}}$
V.TỨ DIỆN ĐỀU
1. Kiến thức cơ bản:
$\bullet$ Tứ diện đều là tứ diện có 6 cạnh bằng nhau, do đó 4 mặt của nó là bốn tam giác đều bằng nhau.
2. Một số bài toán cơ bản
Bài 1. Chứng minh rằng tứ diện đều là tứ diện trực tâm?
Bài giải:
Gọi $I$ là trung điểm của $CD$. Ta có:
$CD\bot AI\,\, \text{và}\,\, CD\bot BI \Rightarrow CD \bot (ABI) \Rightarrow CD\bot AB$
Tương tự như thế ta cũng có: $BC \bot AD$ và $AC \bot BD$.
Vậy: Tứ diện $ABCD$ là tứ diện vuông
Bài 2. Cho tứ diện đều $ABCD$ cạnh a. Tính đường cao tứ diện?
Bài giải:
Vẽ $AH$ vuông góc với $(BCD)$. Do $ADCB$ là tứ diện đều nên $H$ là tâm của tam giác đều $BCD$. Ta có:
$AH^2=AB^2-BH^2=a^2-(\frac{2}{3}-\frac{a\sqrt{3}}{2})^2=\frac{2a^2}{3}$
Vậy: $h=AH=\frac{a\sqrt{6}}{3}$
Bài 3. Cho tứ diện đều $ABCD$ cạnh $a$. Tính thể tích của tứ diện?
Bài giải:
Diện tích tam giác $BCD$: $S_{BCD}=\frac{a^2\sqrt{3}}{4}$
Đường cao tứ diện đều $ABCD$: $h=AH=\frac{a\sqrt{6}}{3}$
Thể tích của tứ diện đều $ABCD$: $V_{ABCD}=\frac{1}{3}S_{BCD}.AH=\frac{a^3\sqrt{2}}{12}$
Bài 4. Cho tứ diện đều $ABCD$, cạnh $a$. Tính bán kính của mặt cầu ngoại tiếp tứ diện $ABCD$?
Bài giải:
$\bullet$ Hạ $AH$ vuông góc với $mp(ABC)$, $AH$ chính là trục của đường tròn ngoại tiếp $\Delta ABC$. Gọi $I$, $J$ lần lượt là trung điểm của $CD$ và $AB$. Do $IA=IB$ nên $IJ$ là trung trực của $AD$ vẽ trong $mp(IAB)$. Giao điểm $O$ của $AH$ và $IJ$ là tâm $O$ của mặt cầu ngoại tiếp tứ diện $ABCD$.
$\bullet$ Tứ giác $OHBJ$ là tứ giác nội tiếp nên:
$AO.AH=AJ.AB \implies AO=R=\frac{AB^2}{2AH}$
Mà ta đã biết đường cao trong tứ giác đều là:
$AH=\frac{a\sqrt{6}}{3}$
Nên: $R=\frac{a\sqrt{6}}{4}$
$\bullet$ Vậy: $R=\frac{a\sqrt{6}}{4}$
Bài 5. Cho tứ diện đều $ABCD$, cạnh $a$. Tính bán kính của mặt cầu nội tiếp tứ diện $ABCD$?
Bài giải:
Ta có: $CD \bot (ABI) \implies (ABI) \bot (ACD)$ (theo giao tuyến $AI$)
Cho nên khoảng cách từ $O$ đến $(ACD)$ là khoảng cách từ $O$ đến $AI$.
Nhưng $IJ$ là phân giác góc $\widehat{AIB}$ nên: $OH=OK$
Vậy $O$ cách đều hai mặt $(BCD)$ và $(ACD)$. Tương tự ta cũng chứng minh tất cả các mặt của tứ diện. Vậy $O$ là tâm của mặt cầu ngoại tiếp tứ diện $ABCD$.
Bán kính của mặt cầu này:
$r=OH=AH-AO=\frac{a\sqrt{6}}{12}$
Vậy: $r=\frac{a\sqrt{6}}{12}$
#685784 ĐỀ THI TUYỂN SINH VÀO 10 THPT NĂM 2017 - 2018 TỈNH BÌNH ĐỊNH MÔN TOÁN
 Posted by
nguyenthanhhung1985
on 28-06-2017 - 05:28
in
Thi tốt nghiệp
Posted by
nguyenthanhhung1985
on 28-06-2017 - 05:28
in
Thi tốt nghiệp
ĐỀ THI TUYỂN SINH VÀO 10 THPT NĂM 2017 - 2018 TỈNH BÌNH ĐỊNH MÔN TOÁN
Câu 1: (1,5 điểm)
Cho $A=\frac{\sqrt{x}}{\sqrt{x}-2}$; $B=\frac{2}{\sqrt{x}+2}+\frac{4\sqrt{x}}{x-4}$
a) Tính $A$ khi $x=9$
b) Thu gọn $T=A-B$
c) Tìm $x$ để $T$ nguyên
Câu 2: (1,5 điểm)
Cho phương trình $x^2-2mx-6m-9=0$
a) Giải phương trình khi $m=0$
b) Tìm $m$ để phương trình có $2$ nghiệm $x_1$, $x_2$ trái dấu thỏa mãn$x_1^2+x_2^2=13$
Câu 3: (2 điểm) Một đám đất hình chữ nhật có chu vi $24m$. Nếu tăng độ dài một cạnh lên $2m$ và giảm độ dài cạnh còn lại $1m$ thì diện tích mảnh đất tăng thêm $1m^2$. Tính độ dài các cạnh của hình chữ nhật ban đầu.
Câu 4:(4 điểm) Cho tam giác $ABC$ $(AB<AC)$ nội tiếp đường tròn tâm $O$. $M$ là điểm nằm trên cung $BC$ không chứa điểm $A$. Gọi $D$, $E$, $F$lần lượt là hình chiếu của $M$ trên $BC$, $CA$, $AB$. Chứng minh:
a) Bốn điểm $M$, $B$, $D$, $F$ cùng thuộc một đường tròn và $M$, $D$, $E$, $C$ cùng thuộc một đường tròn.
b) Chứng minh $D$, $E$, $F$ thẳng hàng.
c) $\frac{BC}{MD}=\frac{AC}{ME}+\frac{AB}{MF}$
Câu 5: (1 điểm) Cho $a$, $b$, $c$ là ba số thực dương. CMR: $\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}\ge a^3+b^3+c^3$
Đáp án:
Câu 1:
a) Khi $x=9$ ta được $A=\frac{\sqrt{9}}{\sqrt{9}-2}=3$
b) ĐK: $x\ge 0,\, x\ne 0$
$T=A-B=\frac{\sqrt{x}}{\sqrt{x}-2}-(\frac{2}{\sqrt{x}+2}+\frac{4\sqrt{x}}{x-4})$
$\,\,\,\,=\frac{\sqrt{x}.(\sqrt{x}+2)-2.(\sqrt{x}-2)-4\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}$
$\,\,\,\,=\frac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}$
$\,\,\,\,=\frac{x-4\sqrt{x}+4}{(\sqrt{x}-2)(\sqrt{x}+2)}$
$\,\,\,\,=\frac{(\sqrt{x}-2)^2}{(\sqrt{x}-2)(\sqrt{x}+2)}$
$\,\,\,\,=\frac{\sqrt{x}-2}{\sqrt{x}+2}$
c) $T=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}$
$T\,\, \text{nguyên khi}\,\, 4 \vdots \sqrt{x}+2$
$\iff \sqrt{x}+2=\mp 1;\, \mp 2; \, \mp 4$
$x=0 \,\, \text{hoặc}\,\, x=4(KTMĐK)$
Vậy: $X=0$
Câu 2:
a) Khi $m=0$ phương trình trở thành:
$x^2-9=0 \iff x=\pm 3$
b) $a=1,\,\,b=-2m,\,\,b'=-m,\,\,c=-6m-9$
$\Delta = b'^2-ac=m^2+6m+9=(m-3)^2 \ge 0,\,\, \forall m$
Phương trình luôn có hai nghiệm $x_1, x_2$ với mọi $m$.
Theo hệ thức Viet ta có: $x_1+x_2=2m \,\, \text{và} \,\, x_1.x_2=-6m-9$
Phương trình có $2$ nghiệm trái dấu $\iff x_.x_2<0 \iff -6m-9<0 \iff m>-\frac{3}{2}$
Ta có:
$x_1^2+x_2^2=13$
$\iff (x_1+x_2)^2-2x_1.x_2=13$
$\iff (2m)^2-2(-6m-9)-13=0$
$\iff m=-\frac{1}{2}$
Vậy: $m=-\frac{1}{2}$
Câu 3:
Gọi $x(m)$ là cạnh thứ nhất của mảnh đất hình chữ nhật
$y(m)$ là cạnh thứ hai của mảnh đất hình chữ nhật.
ĐK: $0<x<12,\,\, 1<y<12$
Diện tích mảnh đất ban đầu: $x.y\,(m^2)$
Theo đề ta có phương trình: $2(x+y)=24 \, (m)$ (1)
Giả sử tăng cạnh thứ nhất $2m$ và giảm cạnh thứ hai $1m$.
Độ dài cạnh thứ nhất khi tăng $2m$: $x+2 \, (m)$
Độ dài cạnh còn lại khi giảm $1m$: $y-1 \,(m)$
Diện tích mảnh đất khi tha đổi: $(x+3)(y-1) \,(m^2)$
Theo đề bài ta có phương trình: $(x+3)(y-1)-xy=1$ (2)
Từ (1), (2) ta được hệ phương trình:
$\left\{\begin{matrix} x+y=12\\-x+2y=3 \end{matrix}\right.$ $\iff \left\{\begin{matrix} x=7\\y=5 \end{matrix}\right.$
Vậy: kích thước mảnh đất lúc ban đầu: $7m,\,\, 5m$
Câu 4:
a) Chứng minh:
Ta có: $MF \bot AB \,\, \text{nên} \,\, \widehat{MFB}=90^0$
$MD \bot BC \,\, \text{nên} \,\, \widehat{MDB}=90^0$
Tứ giác $MDBF$ có $\widehat{MFB}+\widehat{MDB}=90^0+90^0=180^0$
Do đó tứ giác $MDBF$ nội tiếp
Suy ra 4 điểm $M$, $D$, $B$, $F$ cùng thuộc một đường tròn.
Ta có: $MD \bot BC \,\, \text{nên} \,\, \widehat{MDC}=90^0$
$MF \bot AC \,\, \text{nên} \,\, \widehat{MFC}=90^0$
Suy ra $\widehat{MDC}=\widehat{MFC}=90^0$
Suy ra $D$, $F$ cùng nhìn $MC$ dưới $1$ góc bằng nhau.
Do đó $4$ điểm $M$, $D$, $E$, $C$ cùng thuộc một đường tròn.
b) Vì tứ giác $MDBF$ nội tiếp nên $\widehat{M_1}=\widehat{D_1}$ (cùng chắn cung $BF$)
Vì tứ giác $MDEC$ nội tiếp nên $\widehat{M_2}=\widehat{D_2}$
Mặt khác tứ giác $MBAC$ nội tiếp nên $\widehat{B_1}=\widehat{C}$ (góc ngoài của tứ giác nội tiếp)
Do đó $widehat{M_1}=\widehat{M_2}$ (cùng phụ với $\widehat{B_1}$, $\widehat{C}$)
Suy ra: $\widehat{D_1}=\widehat{D_2}$
Mà $\widehat{D_1}+\widehat{BDE}=180^0$
Nên $\widehat{D_1}+\widehat{BDE}=180^0$
Hay $D$, $E$, $F$ thẳng hàng.
c) Ta có
$\frac{AC}{ME}+\frac{AB}{MF}=\frac{AE+EC}{ME}+\frac{AF-FC}{MF}=\frac{AE}{ME}+\frac{EC}{ME}+\frac{AF}{MF}-\frac{FC}{MF}$
$=\tan(\widehat{AME})+\tan(\widehat{M_2})+\tan(\widehat{AMF})-\tan(\widehat{M_1})$
Mà $\widehat{M_1}=\widehat{M_2}$ nên $\frac{AC}{ME}+\frac{AB}{MF}=\tan(\widehat{AME})+\tan(\widehat{AMF})$
Mặt khác: tứ giác $AFME$ nội tiếp nên $\widehat{AME}=\widehat{AFE}=\widehat{BMD}$, $\widehat{AMF}=\widehat{AEF}=\widehat{DMC}$
Do đó
$\frac{AC}{ME}+\frac{AB}{MF}=\tan(\widehat{AME})+\tan(\widehat{AMF})$
$\,\,\,\,=\tan(\widehat{BMD})+\tan(\widehat{MDC})$
$\,\,\,\,=\frac{BD}{MD}+\frac{DC}{MD}$
$\,\,\,\,=\frac{BD+DC}{MD}$
$\,\,\,\,=\frac{BC}{MD}$ (đpcm)
Câu 5:
Cách 1:
$\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}=\frac{a^6}{abc}+\frac{b^6}{abc}+\frac{c^6}{abc}=\frac{(a^3)^2}{abc}+\frac{(b^3)^2}{abc}+\frac{(c^3)^2}{abc}$
Áp dụng bất đẳng thức Cauchy - Schwarz:
$\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}=\frac{(a^3)^2}{abc}+\frac{(b^3)^2}{abc}+\frac{(c^3)^2}{abc}\ge \frac{(a^3+b^3+c^3)^2}{abc+abc+abc}=\frac{(a^3+b^3+c^3)(a^3+b^3+c^3)}{3abc}$
Áp dụng bất đẳng thức AM - GM cho $3$ số $a^3$, $b^3$, $c^3$ ta được:
$a^3+b^3+c^3\ge 3\sqrt[3]{a^3b^3c^3}=3abc$
Do đó
$\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}\ge \frac{(a^3+b^3+c^3)(a^3+b^3+c^3)}{3abc}\ge \frac{(a^3+b^3+c^3)3abc}{3abc}=a^3+b^3+c^3$
Dấu "=" xảy ra khi $a=b=c$
Cách 2:
Áp dụng bất đẳng thức AM - GM cho $2$ số $\frac{a^5}{bc}$, $abc$ ta được:
$\frac{a^5}{bc}+abc\ge 2a^3$
Áp dụng bất đẳng thức AM - GM cho $2$ số $\frac{b^5}{bc}$, $abc$ ta được:
$\frac{b^5}{ca}+abc\ge 2b^3$
Áp dụng bất đẳng thức AM - GM cho $2$ số $\frac{c^5}{bc}$, $abc$ ta được:
$\frac{c^5}{ab}+abc\ge 2c^3$
Cộng vế theo vế: $\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}+3abc\ge 2a^3+2b^2+2c^3=(a^3+b^3+c^3)+(a^3+b^3+c^3)$ (1)
Áp dụng bất đẳng thức AM - GM cho $3$ số $a^3$, $b^3$, $c^3$ ta được:
$a^3+b^3+c^3\ge 3\sqrt[3]{a^3b^3c^3}=3abc$ (2)
Từ (2) vào (1) ta được:
$\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}+3abc\ge (a^3+b^3+c^3)+(a^3+b^3+c^3)\ge a^3+b^3+c^3+3abc$
$\iff \frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}\ge a^3+b^3+c^3$
Dấu "=" xảy ra khi $a=b=c$
Cách 3:
Áp dụng bất đẳng thức AM - GM cho $5$ số $\frac{a^5}{bc}$, $\frac{a^5}{bc}$, $\frac{a^5}{bc}$, $b^3$, $c^3$ ta được:
$\frac{a^5}{bc}+\frac{a^5}{bc}+\frac{a^5}{bc}+b^3+c^3\ge 5a^3$
Áp dụng bất đẳng thức AM - GM cho $5$ số $\frac{b^5}{ca}$, $\frac{b^5}{ca}$, $\frac{b^5}{ca}$, $c^3$, $a^3$ ta được:
$\frac{b^5}{ca}+\frac{b^5}{ca}+\frac{b^5}{ca}+c^3+a^3\ge 5b^3$
Áp dụng bất đẳng thức AM - GM cho $5$ số $\frac{c^5}{ab}$, $\frac{c^5}{ab}$, $\frac{c^5}{ab}$, $a^3$, $b^3$ ta được:
$\frac{c^5}{ab}+\frac{c^5}{ab}+\frac{c^5}{ab}+a^3+b^3\ge 5c^3$
Cộng vế theo vế:
$3(\frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab})+2(a^3+b^3+c^3)\ge 5(a^3+b^3+c^3)$
$\iff \frac{a^5}{bc}+\frac{b^5}{ca}+\frac{c^5}{ab}\ge a^3+b^3+c^3$
Dấu "=" xảy ra khi $a=b=c$
Attached Files
-
 de-thi-vao-lop-10-mon-toan-tinh-binh-dinh-nam-hoc-2017.pdf 319.06KB
167 downloads
de-thi-vao-lop-10-mon-toan-tinh-binh-dinh-nam-hoc-2017.pdf 319.06KB
167 downloads
- Diễn đàn Toán học
- → nguyenthanhhung1985's Content