http://www.mathlinks...1737426#1737426. Bạn tham khảo ở đây nhé!Còn bài 1 mình làm như thế nào???
lamminhbato nội dung
Có 23 mục bởi lamminhbato (Tìm giới hạn từ 04-06-2020)
#225741 Bài số khó
 Đã gửi bởi
lamminhbato
on 10-01-2010 - 16:53
trong
Số học
Đã gửi bởi
lamminhbato
on 10-01-2010 - 16:53
trong
Số học
#224415 Bài số học
 Đã gửi bởi
lamminhbato
on 31-12-2009 - 19:54
trong
Số học
Đã gửi bởi
lamminhbato
on 31-12-2009 - 19:54
trong
Số học
À, em hiểu rồi! Thế thì em đề xuất thế này. Bằng lý luận tương tự như lời giải cuả em, thì mình có thể chứng minh được bài toán tổng quát hơn, đó là:Cách giải cua em khá là thú vị và khá hay. Còn câu 2 thì ý của anh là em có thể đề xuất một số hướng để tổng quát hóa bài toán trên được không
Bài toán Chứng minh rằng với mỗi số nguyên dương $k$ và $n\ge k$ thì tồn tại vô số số có dạng $2^{k}\left (2^{n-k}-1\right )-1$ nguyên tố cùng nhau đôi một.
Ngoài ra, em cũng đang nghĩ về một vấn đề mở như sau:
Vấn đề Tìm tất cả các hằng số $k$ nguyên dương sao cho tồn tài vô hạn các số có có dạng $2^n-k$ đôi một nguyên tố cùng nhau.
#224255 Lớp luyện thi VMO 2010 trên mạng
 Đã gửi bởi
lamminhbato
on 30-12-2009 - 21:02
trong
Seminar Phương pháp toán sơ cấp
Đã gửi bởi
lamminhbato
on 30-12-2009 - 21:02
trong
Seminar Phương pháp toán sơ cấp
#224172 Bài số học
 Đã gửi bởi
lamminhbato
on 30-12-2009 - 11:48
trong
Số học
Đã gửi bởi
lamminhbato
on 30-12-2009 - 11:48
trong
Số học
Cho dãy các số tự nhiên $x_n$ thỏa mãn $x_n=2^n-3$.
1. Chứng minh rằng trong dãy tồn tại vô hạn số đôi một nguyên tố cùng nhau
2. Đề xuất bài toán tổng quát ( cái này quan trọng đây)
$(1)$ Ta chứng minh bằng quy nạp. Dễ dàng kiểm tra được các số $x_3,x_4,x_5$ là các số nguyên tố cùng nhau đôi một. Giả sử tồn tại một dãy $x_{n_1}, x_{n_2}, \ldots, x_{n_k}$ $
$(2)$ Em chưa hiểu ý lắm ạ!
#221470 Đề chọn đội tuyển toán PTNK 2009
 Đã gửi bởi
lamminhbato
on 25-11-2009 - 09:35
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
lamminhbato
on 25-11-2009 - 09:35
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
bài cuối cuả ngày hai, ý tưởng anh Hiếu giống cuả em tối hôm qua, chủ yếu là sử dụng cái bổ đề này trong bài post cuả em (Nhưng chứng minh hơi phức tạp quá ạ!)Đây là lời giải của em. Mọi người xem thử ạ.
http://www.mathlinks...ic.php?t=298677
#213577 com on!
 Đã gửi bởi
lamminhbato
on 06-09-2009 - 22:28
trong
Hình học
Đã gửi bởi
lamminhbato
on 06-09-2009 - 22:28
trong
Hình học
#211127 Một tính chất của đường đối trung
 Đã gửi bởi
lamminhbato
on 20-08-2009 - 21:20
trong
Hình học
Đã gửi bởi
lamminhbato
on 20-08-2009 - 21:20
trong
Hình học
Gọi $O$ là tâm cuả vòng tròn ngoại tiếp tam giác $ABC$
(1) Chứng minh $B,C,B_a,C_a$ đồng viên. Cái này đơn giản thôi! Ta có thể chứng minh theo cách này: Ta có $AB_aA_1C_a$ là hình bình hành do đó $AA_1,B_aC_a$ cắt nhau tại trung điểm mỗi đường. Ta lại thấy rằng $AA_1$ là đường đối trung cuả $\triangle ABC$. Từ đó dẫn đến rằng $B_aC_a,BC$ là hai đường đối song wrt $\angle A$ $\Rightarrow$ $B,C,B_a,C_a$ đồng viên.
(2) Chứng minh $AO_a,BO_b,CO_c$ đồng quy. Từ gt bài toán rằng: "... chọn $B_a,C_a$ trên $AB,AC$ lần lượt sao cho $AB_aA_1C_a$ là hình bình hành..." khiến cho ta suy nghĩ tự nhiên đến một hướng giải quyết sau:
Đặt $k=\dfrac {AA_1}{AK}$, trong đó $K$ là điểm symmedian wrt $\triangle ABC$. Xét phép vị tự tâm $A$, tỉ số $k$, ta có $\mathcal {V}(A,k)$ $:B\mapsto B'$, $C\mapsto C'$, $K\mapsto A_1$. Khi ấy $\triangle ABC\mapsto \triangle AB'C'$ đồng thời $A_1$ cũng sẽ là điểm symmendian wrt $\triangle AB'C'$. Lại để ý rằng, qua $A_1$ ta đã có các đường thằng $A_1B_a,A_1C_1,$ $\overline {BA_1C}$ song song lần lượt với $AC',AB',B'C'$ do đó $(BCC_aB_a)$ chính là đường tròn Lemoine thứ nhất cuả $A_1$ wrt $\triangle AB'C'$. Khi ấy $O_a$ lúc này đóng vai trò là tâm cuả đường tròn Lemoine nói trên sẽ là trung điểm cuả $A_1O'$, trong đó $O'$ là tâm vòng tròn ngoại tiếp tam giác $AB'C'$. Mặt khác $A_1O'|| KO$ (chú ý là qua phép vị tự $V(A,k)$). Do đó $AO_a$ đi qua trung điểm cuả $KO$. Lập luận tương tự cho $BO_b$, $CO_c$. Từ đây ta có đpcm. $\square$
#207257 Một bài tổ hợp khó
 Đã gửi bởi
lamminhbato
on 30-07-2009 - 22:56
trong
Tổ hợp và rời rạc
Đã gửi bởi
lamminhbato
on 30-07-2009 - 22:56
trong
Tổ hợp và rời rạc
Hoặc là từ $g(n)=8g(n-1)+9g(n-2)$ ta cũng có thể suy ra $g(n)$ có dạng $a(-1)^n+b9^n$ (Do $-1$ và $9$ là hai nghiệm của phương trình $X^2-8X-9=0$). Sau đó thay $n=1$ và $n=2$ vào ta cũng tìm được công thức như trên. Kiến thức này hình như không được đưa vào chương trình phổ thông.
Bài giải của em bên kia bị ẩu rồi anh ạ! Mình đếm "đểu" quá. Em xin được giải và trình bày lập luận chi tiết lại như sau:
Xét $S_n=\{a=\overline {d_1d_2...d_n}|$ $a$ $\vdots$ $5,$ $d_i\neq d_{i+1}\}$ là tập hợp chứa các số thoải yêu cầu bài toán. Đặt $|S_n|=a_n$.
Ta chia $S_n$ thành hai tập con rời nhau thoả mãn $S_n=A_n\cup B_n$; trong đó $A_n=\{a=\overline {d_1d_2...d_n}|$ $\overline {d_1...d_{n-1}}$ $\vdots$ $5\}$ và $B_n=\{b=\overline {d_1d_2...d_n}|$ $5$ $\nmid$ $\overline {d_1...d_{n-1}}\}$
$\bullet$ Loại 1: Xét $A_n$
Mỗi phần tử của $A_n$ được đặt tương ứng với duy nhất một phần tử thuộc $S_{n-1}$. Do đó tồn tại một song ánh $f$ sao cho $f: A_n\longrightarrow S_{n-1}$. Do đó $|A_n|=|S_{n-1}|=a_{n-1}$. $(1)$
$\bullet$ Loại 2: Xét $B_n$
Ta có nhận xét rằng với mỗi số $b'=\overline {d_1d_2...d_{n-1}}$ sao cho $5\nmid b'$ sẽ cho ra 2 số $b\in B_n$. Do đó $|B_n|=2|B'_{n}|$, trong đó $B'_{n}$ là tập chứa các số $b'$. Ta chia $B'_{n}$ thành hai tập rời nhau thỏa mãn $B'_{n}=C_n\cup D_n$; trong đó $C_n=\{c=\overline {d_1d_2...d_{n-1}}|$ $\overline {d_1d_2...d_{n-2}}$ $\vdots 5\}$ và $D_n=\{d=\overline {d_1d_2...d_{n-1}}|$ $5\nmid$ $\overline {d_1d_2...d_{n-2}}\}$
a) Xét loại $C_n$
Cứ mỗi $c'=\overline {d_1d_2...d_{n-2}}$ sẽ tương ứng với một phần tử thuộc $S_{n-2}$. Do đó nếu gọi $C'_n$ là tập hợp chứa các số $c'$ thì $|C'_{n}|=|S_{n-2}|=a_{n-2}$. Nhưng mỗi phần tử thuộc $C'_{n}$ lại tương ứng với 8 phần tử thuộc $C_n$ (Vì bản thân $d_{n-2}\in \{0,5\}$ cho nên $d_{n-1}$ có 8 cách chọn để tạo thành một phần tử thuộc $B'_{n}$). Do đó $|C_n|=8|C'_{n}|=8.a_{n-2}$. $
b) Xét loại $D_n$
Mỗi số $d'=\overline {d_1d_2...d_{n-2}}$ $\leftrightarrow$ $b'$. Mặt khác số các số $b'$ chính là $|B'_{n}|=\dfrac {|B_n|}{2}$ $=\dfrac {|S_n|-|A_n|}{2}$ $=\dfrac {a_n-a_{n-1}}{2}$. Do đó nếu gọi $D'_{n}$ là tập chứa các số $d'$ thì ta có $|D'_n|=\dfrac {a_{n-1}-a_{n-2}}{2}$. Nhưng mỗi số $d'$ lại tương ứng với 7 phần tử thuộc $D_n$ (Vì với $d_{n-2}\neq \{0,5\}$ cho nên $d_{n-1}$ lúc này không được nhận $\{0,5\}$ và cả số đã được chọn ở $d_{n-2}$ nên nó chỉ còn 7 cách chọn để tạo thành một phần tử thuộc $B'_n$). Do đó $|D_n|=7|D'_n|=\dfrac {7(a_{n-1}-a_{n-2})}{2}$. $(**)$
Từ $
Do đó $|B_n|=9a_{n-2}+7a_{n-1}$. $(2)$
Cho nên từ $(1)$ và $(2)$ ta có được công thức truy hồi $a_n=8a_{n-1}+9a_{n-2}$.
Đến đây chắc em làm đúng rồi
#206912 Một bài tổ hợp khó
 Đã gửi bởi
lamminhbato
on 28-07-2009 - 18:54
trong
Tổ hợp và rời rạc
Đã gửi bởi
lamminhbato
on 28-07-2009 - 18:54
trong
Tổ hợp và rời rạc
Anh xem kỹ hộ em dc chứ ạ!A chưa đọc kỹ cách giải của em bên kia. Căn bản công thức truy hồi của anh là cấp 2 (tức là tính đến hai số hạng trước của dãy) công thức của em là truy hồi cấp 1 (tức là tính theo một số hạng phía trước của dãy). Kết quả ở đây thì a check đúng 100% rồi. E thử check xem với công thức của em thì kết quả có y hệt không? Nếu kết quả giống thì khả năng cách giải của e cũng đúng. Nếu khác thì xem xét lại xem thế nào!
#206801 Một bài tổ hợp khó
 Đã gửi bởi
lamminhbato
on 27-07-2009 - 23:51
trong
Tổ hợp và rời rạc
Đã gửi bởi
lamminhbato
on 27-07-2009 - 23:51
trong
Tổ hợp và rời rạc
#200124 Đa thức (biến đổi thông minh và uyển chuyển)
 Đã gửi bởi
lamminhbato
on 04-06-2009 - 11:12
trong
Các dạng toán khác
Đã gửi bởi
lamminhbato
on 04-06-2009 - 11:12
trong
Các dạng toán khác
1,$P(x)=x^3+ax^2+bx+c$
$Q(x)=x^2+x+2007$
Biết P(x) có 3 nghiệm phân biệt và P(Q(x)) ko có nghiệm
CMR:$p(2007)>\dfrac{1}{64}$
Câu $1$
Gọi $r_1,r_2,r_3$ là nghiệm cuả $P(x)\Rightarrow P(x)=(x-x_1)(x-x_2)(x-x_3)$
Vì $P(Q(x))$ vô nghiệm nên pt $x^2+x+2007-x_i=0$ vô nghiệm $\Rightarrow 2007-x_i>\dfrac {1}{4}$
$\Rightarrow P(2007)=(2007-x_1)(2007-x_2)(2007-x_3)>\dfrac {1}{4^3}$
Từ đây ta có $QED$.
REMARK- Bài toán này có thể tổng quát được cho đa thức $P$ có $degP=n$, cụ thể như sau:
"Cho $P(x)=x^n+a_nx^{n-1}+a_{n-1}x^{n-2}+...+a_2x+a_1$, $Q(x)=x^2+x+k$
Trong đó $P,Q\in \mathbb {R}[x]$, $P(x)$ có đúng $n$ nghiệm, $k$ là hằng số dương ko đổi.
CMR: $P(k)>\dfrac {1}{4^n}$"
#198022 một bài tổ hợp
 Đã gửi bởi
lamminhbato
on 18-05-2009 - 13:25
trong
Tổ hợp - Xác suất và thống kê - Số phức
Đã gửi bởi
lamminhbato
on 18-05-2009 - 13:25
trong
Tổ hợp - Xác suất và thống kê - Số phức
Em làm thế này, thầy Nam Dũng xem em tiếp cận đúng không ạ?Bài này thú vị đấy. Không có ai giải à? Mọi người có vẻ ngán tổ hợp nhỉ?
Em ký hiệu nếu hai chiếc tất mà cùng 1 đôi thì ký hiệu cùng 1 số.
Bằng song ánh em chuyển về bài toán sau:
Xét A={1,2,3,4,5}. Hỏi có bao nhiêu số có 10 chử số dc tạo bởi 5 chữ số từ A trong đó mỗi chữ số lặp lại đúng 2 lần và ko có số nào đứng 2 vị trí liên tiếp.
Đây là bài wen thuộc rồi ạ!
#197854 bất đẳng thức lượng giác :)
 Đã gửi bởi
lamminhbato
on 16-05-2009 - 00:37
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
lamminhbato
on 16-05-2009 - 00:37
trong
Bất đẳng thức - Cực trị
#197304 Thông báo về cách gõ TEX mới và nhanh
 Đã gửi bởi
lamminhbato
on 08-05-2009 - 13:00
trong
Công thức Toán trên diễn đàn
Đã gửi bởi
lamminhbato
on 08-05-2009 - 13:00
trong
Công thức Toán trên diễn đàn
Cho $a,b,c\in \mathbb R$. CMR:$\sum a^2 \ge 0$
#197280 (13-2a-3b)(13-2c-3d)(13-ac-bd)<=?
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 21:59
trong
Bất đẳng thức và cực trị
Đã gửi bởi
lamminhbato
on 07-05-2009 - 21:59
trong
Bất đẳng thức và cực trị
Bài này hay, bạn xem lời giải cuả mình nhé: http://www.mathlinks...ic.php?t=273726Cho các số thực a,b,c,d thỏa mãn $ a^{2}+b^{2}= c^{2}+d^{2}= 13.$
Tìm giá trị lớn nhất của
$ S=(13-2a-3b)(13-2c-3d)(13-ac-bd). $
Good lucks.
#197269 Phép nghịch đảo đây
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:18
trong
Hình học phẳng
Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:18
trong
Hình học phẳng
Xem lời giải cuả mình ở đây, bài post cuối cùng http://www.mathlinks...ic.php?t=274672CMR 1 đường tròn qua 3 trung điểm của các cạnh tam giác thì nó sẽ tiếp xúc với 3 đường tròn bàng tiếp của tam giác đó.(Định lý Fuerbach)
#197268 Bài toán này không biết giải
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:13
trong
Hình học phẳng
Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:13
trong
Hình học phẳng
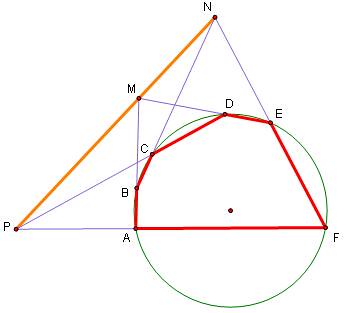
Bài này khá hay, nhưng chưa hết hạn, mình gợi ý: bài này liên quan đến điểm $Feurebach$ wrt $\triangle ABC$.THTT phải kok bạn cái này hết hạn chưa vậy ?
mình chỉ đoán ra EF tiếp xúc với đường tròn tâm (O)_ bán kính 1/2 r (còn chưa làm ra)
#197267 đường thẳng đi qua điểm cố định....(cần giúp đỡ)
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:02
trong
Phương pháp tọa độ trong mặt phẳng
Đã gửi bởi
lamminhbato
on 07-05-2009 - 19:02
trong
Phương pháp tọa độ trong mặt phẳng
#197265 Những định nghĩa và tính chất cơ bản
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 18:37
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Đã gửi bởi
lamminhbato
on 07-05-2009 - 18:37
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Có 1 cách C/m định lý Pascal bằng tỷ số kép, khá hay. Mọi người tham khảo bài c/m cuả Mashimaru.<span style='font-size:14pt;line-height:100%'><span style='color:red'>Định lí Pascal</span></span>
Định lý: Cho lục giác ABCDEF nội tiếp. Khi đó các giao điểm của các cặp cạnh đối AB và DE, BC và EF, CD và FA đồng quy.
http://www.mathlinks...ic.php?t=274672
#197264 Đường đối trung của tam giác
 Đã gửi bởi
lamminhbato
on 07-05-2009 - 18:33
trong
Hình học
Đã gửi bởi
lamminhbato
on 07-05-2009 - 18:33
trong
Hình học
Cho tam giác ABC, vẻ các trung tuyến AM,BN,CP và các phân giác AD,BE,CF. Trên BC,CA,AB lần lượt lấy X,Y,Z sao cho AX,BY,CZ là các đường đối trung của tam giác ABC. Chứng minh rằng: AX,BY,CZ đồng qui.
Đây là bài toán quen thuộc.
Trứớc tiên ta có nhận xét:$AX,BY,CZ$ sẽ đi qua đối cực cuả $BC,CA,AB$ wrt $(ABC)$.
Như vậy, nếu gọi $A_0,B_0,C_0$ là giao điểm các tiếp tuyến tại $A,B,C$ cuả $(O)$ cắt nhay từng đôi một, $A_0$ đối diện với $A$.... Khi đó $AA_0,BB_0,CC_0$ đồng quy tại điểm Gergone wrt $\triangle A_0B_0C_0$.
#187513 Đề+lời giải NK Toán Chuyên 08-09 (tp HCM)
 Đã gửi bởi
lamminhbato
on 30-06-2008 - 11:19
trong
Tài liệu - Đề thi
Đã gửi bởi
lamminhbato
on 30-06-2008 - 11:19
trong
Tài liệu - Đề thi
File gửi kèm
-
 NK_toan_08_09.doc 250.5K
64 Số lần tải
NK_toan_08_09.doc 250.5K
64 Số lần tải
#186320 Kì thi tuyển sinh toán chuyên NK Tp HCM 08-09
 Đã gửi bởi
lamminhbato
on 03-06-2008 - 20:59
trong
Tài liệu - Đề thi
Đã gửi bởi
lamminhbato
on 03-06-2008 - 20:59
trong
Tài liệu - Đề thi
File gửi kèm
-
 NK_toan_08_09.doc 45K
85 Số lần tải
NK_toan_08_09.doc 45K
85 Số lần tải
#184828 Ai giúp em bài của Titu
 Đã gửi bởi
lamminhbato
on 08-05-2008 - 10:18
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
lamminhbato
on 08-05-2008 - 10:18
trong
Bất đẳng thức - Cực trị
File gửi kèm
-
 Titu_1997.doc 16K
23 Số lần tải
Titu_1997.doc 16K
23 Số lần tải
- Diễn đàn Toán học
- → lamminhbato nội dung