Cho $k$ là một trường. Cho $\mathbf{Vect}_k$ và $\mathbf{Set}$ lần lượt là phạm trù các $k$-không gian véctơ và phạm trù các tập hợp. Cho $n$ là số nguyên dương tùy ý và xét hàm tử $F: \mathbf{Vect}_k \to \mathbf{Set}$ cho bởi:

• Với mỗi không gian véctơ $V$, $F(V)$ là tập hợp $V^n$.
• Với mỗi ánh xạ tuyến tính $f: V \to W$, $F(f): V^n \to W^m$ là ánh xạ cho bởi $(v_1,\ldots,v_n) \mapsto (f(v_1),\ldots,f(v_n))$.

Ta chỉ ra rằng $F$ là hàm tử biểu diễn được, nghĩa là tồn tại không gian véctơ $E$ cùng một đẳng cấu hàm tử $F \cong \text{Hom}_k(E,-)$. Nói cách khác, ta muốn một đẳng cấu $V^n \cong \text{Hom}_k(E,V)$, và đẳng cấu này tự nhiên theo $V$. Bằng chữ, điều này có nghĩa là: "cho một bộ $n$ phần tử của $V$ cũng chính là cho một ánh xạ tuyến tính từ $E$ vào $V$." Không khó để thấy rằng, đại biểu thích hợp cho $E$ là một không gian véctơ $n$-chiều, vì cho một ánh xạ tuyến tính từ một không gian $n$-chiều vào $V$ chính là cho một bộ $n$ phần tử của $V$.

 

Vậy ta lấy $E = k^n$ và xây dựng đẳng cấu hàm tử $\Phi: F \to \text{Hom}_k(k^n,-)$ như sau. Với mỗi không gian véctơ $V$, ta định nghĩa ánh xạ $\Phi(V): V^n \to \text{Hom}_k(k^n,V)$ bằng cách: với mỗi $(v_1,\ldots,v_n) \in V^n$, $\Phi(V)(v_1,\ldots,v_n): k^n \to V$ là ánh xạ tuyến tính $\alpha$ cho bởi công thức $$\alpha: k^n \to V, \qquad \alpha(a_1,\ldots,a_n) = a_1v_1 + \cdots + a_n v_n,$$ nói cách khác là $\alpha$ được xác định duy nhất bởi công thức $\alpha(e_i) = v_i$ với $i=1,\ldots,n$, trong đó $(e_1,\ldots,e_n)$ là cơ sở chính tắc của $k^n$. Dễ thấy $\Phi(V)$ là một song ánh.

 

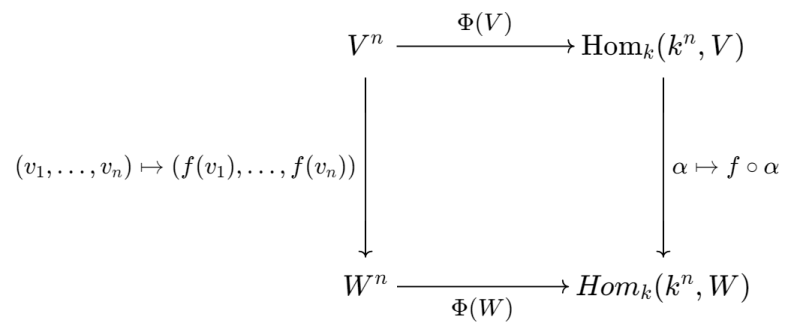
Ta còn phải chỉ ra rằng $\Phi$ là một biến đổi tự nhiên từ hàm tử $F$ vào hàm tử $\text{Hom}_k(k^n,-)$. Điều này có nghĩa là với mỗi ánh xạ tuyến tính $f: V \to W$, ta có biểu đồ giao hoán sau 

Thật vậy, xét $(v_1,\ldots,v_n) \in V^n$ tùy ý. Khi đó $\Phi(V)(v_1,\ldots,v_n)$ là ánh xạ tuyến tính $\alpha: k^n \to V$ cho bởi công thức $$\alpha: k^n \to V, \qquad \alpha(a_1,\ldots,a_n) = a_1v_1 + \cdots + a_n v_n.$$ Mặt khác, $\Phi(W)((f(v_1),\ldots,f(v_n))$ là ánh xạ tuyến tính $\beta: k^n \to W$ cho bởi công thức $$\beta: k^n \to W, \qquad \beta(a_1,\ldots,a_n) = a_1 f(v_1) + \cdots + a_n f(v_n).$$ Ta có $f \circ \alpha = \beta$, nên biểu đồ trên giao hoán. Vậy $\Phi$ là một đẳng cấu tự nhiên từ hàm tử $F$ vào hàm tử $\text{Hom}_k(k^n,-)$, nói cách khác là hàm tử $F$ biểu diễn được bởi vật $k^n$.

Giải đấu trên $3$ vận động viên với $3$ người vô địch tương đối.

Giải đấu trên $4$ vận động viên với $3$ người vô địch tương đối.

GIải đấu trên $6$ vận động viên với $6$ người vô địch tương đối.

Ta gọi một “giải đấu” trên $n$ vận động viên là một cách gán thắng/thua cho từng trận đấu (trong tổng cộng $\frac{n(n-1)}{2}$ trận đấu).

Dễ dàng xây dựng giải đấu trên $3$ cũng như $4$ vận động viên sao cho có $3$ vận động viên vô địch tương đối. Do đó $S_3 = 3$ và $S_4 \ge 3$.

Để chứng minh $S_4 < 4$, ta xét một giải đấu tuỳ ý trên $4$ vận động viên.

• Nếu có một vận động viên $a$ thắng cả $3$ trận thì các vận động viên còn lại không thể viết được tên $a$, nên họ đều không vô địch tương đối.
• Nếu có một vận động viên $a$ thua cả $3$ trận thì anh ta không thể viết tên ai, nên không vô địch tương đối.
• Trường hợp còn lại, mỗi vận động viên đều thắng đúng $1$ hoặc $2$ trận. Mà tổng số trận đấu là $6$ nên có đúng $2$ vận động viên chỉ thắng $1$ trận, gọi họ là $a$ và $b$ và giả sử rằng $a$ thắng $b$. Rõ ràng $a$ chỉ viết được tên của $b$ và người duy nhất mà $b$ thắng, nên $a$ không vô địch tương đối.

Tóm lại, không tồn tại giải đấu trên $4$ vận động viên mà cả $4$ đều vô địch tương đối, vậy $S_4 < 4$, hay $S_4 = 3$.

Tiếp theo, ta định nghĩa một “tam giác” là một bộ $3$ vận động viên $a,b,c$ mà $a$ thắng $b$, $b$ thắng $c$ và $c$ thắng $a$. Ta có nhận xét sau: một giải đấu có cả $n$ vận động viên đều vô địch tương đối khi và chỉ khi mỗi cặp vận động viên đều nằm trong một tam giác nào đó.

Từ nhận xét trên, ta chứng minh khẳng định sau: nếu $S_n = n$ thì $S_{n+2} = n+2$. Thật vậy, giả sử tồn tại một giải đấu $n$ vận động viên sao cho cả $n$ người đều vô địch tương đối. Ta thêm hai vận động viên mới là $a$ và $b$, và xây dựng giải đấu mới trên tất cả $n+2$ vận động viên này bằng cách quy định: $a$ thắng $b$, $b$ thắng tất cả $n$ vận động viên cũ, và tất cả vận động viên cũ thắng $a$. Dễ thấy lúc này, mọi cặp vận động viên đều nằm trong một tam giác nào đó, nên ta thu được một giải đấu với $n+2$ vận động viên đều vô địch tương đối.

Từ đó dễ thấy $S_n = n$ với mọi $n \ge 3$ và lẻ.
Ta cũng xây dựng được giải đấu với $6$ vận động viên đều vô địch tương đối, nên $S_6 = 6$, từ đó $S_n = n$ với mọi $n \ge 6$ và chẵn.

Giả sử phản chứng rằng chỉ có một số hữu hạn các số nguyên tố như vậy, gọi chúng là $q_1,\ldots,q_r$. Xét các số nguyên dương $$N = p q_1\cdots q_r, \quad \text{và} \quad M = N^{p-1} + N^{p-2} + \cdots + 1 = \frac{N^p - 1}{N - 1}.$$ Vì $M > 1$ nên nó có một ước nguyên tố $q$ nào đó.

Một mặt, $M$ và $N$ nguyên tố cùng nhau nên $q \not \kern -.5pt |  N$, hay $q \notin \{p, q_1,\ldots,q_r\}$.

Mặt khác, $q | M$ nên $q | N^p - 1$, hay $N^p \equiv 1 \pmod q$. Nói riêng, tồn tại số nguyên dương $h$ sao cho $N^h \equiv 1 \pmod q$. Theo nguyên lý sắp thứ tự tốt trong $\mathbb{N}$ thì tồn tại số nguyên dương $h$ nhỏ nhất sao cho $N^h \equiv 1 \pmod q$. Thực hiện phép chia Euclid $$p = ah + b, \qquad a \in \mathbb{N}, b \in \{0,1,\ldots,h-1\}.$$ Ta có $$1 \equiv N^p \equiv N^{ah+b} \equiv (N^h)^a \cdot N^b \equiv N^b \pmod q.$$ Theo định nghĩa của $h$ thì ta phải có $b = 0$ (vì nếu $b > 0$ thì $b$ là một số nguyên dương nhỏ hơn $h$ thỏa mãn $N^b \equiv 1 \pmod q$. Vậy $p = ah$, suy ra $h \in \{1,p\}$.

• Nếu $h = 1$ thì $N \equiv 1 \pmod q$, suy ra $$0 \equiv M \equiv N^{p-1} + N^{p-2} + \cdots + 1 \equiv 1 + 1 + \cdots + 1 \equiv p \pmod q,$$ hay $q | p$, suy ra $q = p$, mâu thuẫn.
• Nếu $h = p$, ta áp dụng định lý nhỏ Fermat, $N^{q-1} \equiv 1 \pmod q$. Lại thực hiện phép chia Euclid $q-1$ cho $h$ tương tự như trên, ta có $h | q-1$, hay $p | q-1$, hay $q$ có dạng $pk + 1$. Mà $q \notin \{q_1,\ldots,q_r\}$ và $q_1,\ldots,q_r$ là tất cả các số nguyên tố có dạng $pk+1$ theo giả thiết phản chứng, dẫn đến mâu thuẫn.

Tóm lại giả sử phản chứng là sai, nên có vô số số nguyên tố dạng $pk+1$.

Bình luận: Đánh giá trên được chứng minh một cách sơ cấp nhưng mình đã tìm ra nó bằng cách không sơ cấp, cụ thể là $$\frac{1}{\sqrt[3]{n}} > \int_n^{n+1} \frac{dx}{\sqrt[3]{x}} = \frac{3}{2}\sqrt[3]{x^2} \Bigg |_{x=n}^{x=n+1} = \frac{3}{2}\left(\sqrt[3]{(n+1)^2} - \sqrt[3]{n^2}\right).$$

 

Đánh giá sau đây khá chặt: $\frac{1}{\sqrt[3]{n}} > \frac{3}{2}\left(\sqrt[3]{(n+1)^2} - \sqrt[3]{n^2}\right)$. Từ bất đẳng thức này ta có $$1 + \frac{1}{\sqrt[3]{2}} + \cdots + \frac{1}{\sqrt[3]{n}} > \frac{3}{2}\left(\sqrt[3]{(n+1)^2} - 1\right).$$ Lần lượt thay $n = 15$ và $n = 2009$, ta thu được các kết quả bạn muốn.

Để chứng minh bất đẳng thức trên, ta chia hai vế cho $\sqrt[3]{n^2}$ để thu được $\frac{1}{n} > \frac{3}{2}\left(\sqrt[3]{\left(1+\frac{1}{n}\right)^2} - 1\right)$. 

Bất đẳng thức trên đúng, vì với $x > 0$, ta có các biến đổi tương đương $$x > \frac{3}{2}\left(\sqrt[3]{(1+x)^2} - 1\right) \Leftrightarrow \left(1 + \frac{2}{3}x\right)^3 > (1+x)^2 \Leftrightarrow \frac{1}{3}x^2 + \frac{8}{27}x^3 > 0,$$ và bất đẳng thức cuối cùng hiển nhiên đúng.

 

Nếu k mở rộng hơn,không chỉ giới hạn trong 15 nữa thì làm thế nào vậy thầy.

Ví dụ: Chứng minh $\frac{1}{\sqrt[3]{1}}+\frac{1}{\sqrt[3]{2}}+...+\frac{1}{\sqrt[3]{2009}}>237$. Em đã áp dụng bất đẳng trên nhưng giả không được

 

Đánh giá sau đây khá chặt: $\frac{1}{\sqrt[3]{n}} > \frac{3}{2}\left(\sqrt[3]{(n+1)^2} - \sqrt[3]{n^2}\right)$. Từ bất đẳng thức này ta có $$1 + \frac{1}{\sqrt[3]{2}} + \cdots + \frac{1}{\sqrt[3]{n}} > \frac{3}{2}\left(\sqrt[3]{(n+1)^2} - 1\right).$$ Lần lượt thay $n = 15$ và $n = 2009$, ta thu được các kết quả bạn muốn.

Để chứng minh bất đẳng thức trên, ta chia hai vế cho $\sqrt[3]{n^2}$ để thu được $\frac{1}{n} > \frac{3}{2}\left(\sqrt[3]{\left(1+\frac{1}{n}\right)^2} - 1\right)$. 

Bất đẳng thức trên đúng, vì với $x > 0$, ta có các biến đổi tương đương $$x > \frac{3}{2}\left(\sqrt[3]{(1+x)^2} - 1\right) \Leftrightarrow \left(1 + \frac{2}{3}x\right)^3 > (1+x)^2 \Leftrightarrow \frac{1}{3}x^2 + \frac{8}{27}x^3 > 0,$$ và bất đẳng thức cuối cùng hiển nhiên đúng.

Con lắc đơn không dao động điều hòa. Khi lập phương trình chính xác và không dùng phép làm tròn $\sin x \approx x$, nghiệm của phương trình vi phân thu được có dạng tích phân elliptic, và ta biết rằng tích phân elliptic thì không biểu diễn được dưới dạng hàm sơ cấp: http://ed.quantum-bg...c-integrals.pdf.

Ký hiệu $s(k)$ là tổng các chữ số của một số tự nhiên $k$ và $$S_n = \sum_{k < n} s(k).$$ Ta cần tính $S_n + s(n)$.
Ta có thể tính $S_n$ bằng đệ quy với công thức $$\begin{cases} S_0 = 0 \\ S_n = 10S_m + 45m + r \cdot s(m) + \frac{r(r-1)}{2}\end{cases}$$ với $m = \left\lfloor\frac{n}{10}\right\rfloor$ và $r = n-10m$.
Thật vậy, theo định nghĩa trên thì $m$ và $r$ lần lượt là phần chục và chữ số hàng đơn vị của $n$. Mỗi số tự nhiên $k < n$ có dạng $k = 10m' + r'$ với $m' < m$ và $r' \in \{0,1,\ldots,9\}$ hoặc $k = 10m + r'$ với $r' \in \{0,1,\ldots,r-1\}$. Do đó $$\begin{align*} S_n & = \sum_{m' < m} \sum_{r' = 0}^9 s(10m' + r') + \sum_{r'=0}^{r-1}s(10m+r) \\ & = \sum_{m' < m} \sum_{r' = 0}^9 (s(m') + r') + \sum_{r'=0}^{r-1} (s(m)+r') \\ & = \sum_{m' < m} (10s(m') + 45) + r \cdot s(m) + \frac{r(r-1)}{2} \\ & = 10 S_m + 45m + r \cdot s(m) + \frac{r(r-1)}{2}.\end{align*}$$
Để xác định độ phức tạp về thời gian $T(n)$ khi tính theo công thức truy hồi trên, nhận xét rằng $$T(n) = T\left(\frac{n}{10}\right) + O(\log n),$$ nên theo định lý Master thì $T(n) = O(\log^2 n)$, tức là bằng hàm đa thức bậc hai theo cỡ của input. Từ công thức truy hồi trên có thể tính ra $S_n + s(n)$ theo các chữ số của $n$, nhưng mình chưa đủ kiên nhẫn để thử.

chắc anh nhầm với thầy Nguyễn Minh Hà ở CSP. Thầy Lê Minh Hà là giám đốc điều hành VIASM, chuyên ngành Tôpô đại số.

Giờ mới để ý là bản dịch tiếng Việt này nằm trên trang chính chủ của tác giả luôn. Người dịch là Lê Minh Hà, không biết có phải là thầy Lê Minh Hà phụ trách hình học phẳng cho tạp chí THTT và Toán Tuổi thơ không nhỉ.

Tác giả Milne có tâm thật, viết rất nhiều sách mà sách nào cũng để PDF miễn phí, có cả bản tối ưu dành cho điện thoại máy tính bảng nữa. Rất mong chờ đọc cuốn "2050 Arithmetic Duality Theorems, third edition, first draft" trong 27 năm nữa

Diễn đàn cần nhiều bài như này nữa ạ

Chứng minh này sai ở dòng (3.11). Tác giả đã ngộ nhận rằng "với $p_m$ là ước nguyên tố lớn nhất của $n$ thì tổng $$\sum_{\substack{d|n \\ d \ge p_m}} d$$ chia hết cho $p_m$".

 

Thú thật là mình không đủ trình độ để đọc chứng minh của bạn.

 

Xin gửi kèm một chứng minh khác để mọi người tham khảo

 

2101.07176.pdf

 

Chứng minh này cũng có một lỗi sai nào đó, và mình không đủ trình độ để tìm ra.

Xin lỗi các anh, giờ em mới trả lời được

Em thi ĐGNL của ĐHQG nên được xét tuyển sớm anh.
 

Em đã có dự định du học nhưng vẫn chưa rõ đi khi nào, đi đâu và phải học như thế nào để du học nên anh chị nào đã du học có thể tư vấn giúp em được không ạ

Trước hết, hãy học toán tốt ở trường để có hồ sơ đẹp. Ví dụ đi du họ ở châu Âu thì họ sẽ đánh giá cao khoản này. Sau đó nghiên cứu xem muốn đi nước nào. Chẳng hạn đi Mỹ thì cày thêm TOEFL ở ngoài, cày GRE, tìm hiểu các trường và tiêu chí của họ là gì để đáp ứng. Đi Pháp thì có rất nhiều chương trình như Labex, MathForVietnam… Nói chung bạn nên khoanh vùng thêm là muốn đi học ở đâu, muốn học trường nào… để mọi người dễ tư vấn.

Gọi $d$ là đường phân giác của $\widehat{MIB}$ cũng như của $\widehat{NIC}$ (bằng cộng góc, ta dễ thấy $M, I, C$ thằng hàng và $N, I, B$ thằng hàng). Phép đối xứng qua đường thẳng $d$ biến $B$ thành $M$, biến $C$ thành $N$ và biến $(I)$ thành chính nó. Vì $(I)$ nội tiếp $\triangle ABC$ nên để chứng minh nó nội tiếp $\triangle DMN$ thì ta chỉ cần chứng minh rằng $D$ và $A$ đối xứng với nhau qua $d$.
Thật vậy, một mặt, nếu ký hiệu bởi $r$ bán kính của $(I)$ thì từ chỗ $\widehat{ABI} = 30^\circ$ ta tính được $IA = 2r = ID$.
Mặt khác, $$\widehat{AIM} = \widehat{ACI} + \widehat{CAI} = \frac{\widehat{ACB} + \widehat{BAC}}{2} = \frac{180^\circ - \widehat{ABC}}{2} = 90^\circ - \widehat{IBC} = \widehat{BID}$$ nên $d$ cũng là đường phân giác của $\widehat{AID}$. Từ đó suy ra rằng $A$ và $D$ đối xứng với nhau qua $d$, chính là điều ta muốn.

$B, I, N$ thẳng hàng và $C, I, M$ thẳng hàng.

$M, A, N$ cùng thuộc cung $60^{\circ}$ dựng trên đoạn $BC$.

Tính được $\angle AMB=\angle DBM$, hơn nữa $MA=MB=BD$ suy ra $\triangle MAB=\triangle BMD$. Do đó $MD=BA$.
Chứng minh tương tự $ND=AC$.
Thêm vào đó $MN=BC$ do $\triangle IMN=\triangle IBC$.
Như vậy $\triangle DMN=\triangle ABC$ (c.c.c).

Từ đây ta có $\angle MDN=\angle BAC=60^{\circ}$, dẫn tới $B, D, C$ cùng thuộc cung $60^{\circ}$ dựng trên đoạn $MN$.
Mà $CD=CN$, $BD=BM$ suy ra $IM, IN$ lần lượt là tia phân giác của hai góc $DMN, DNM$.

Từ chỗ $IM$ và $IN$ là hai đường phân giác mới suy ra được $I$ là tâm đường tròn ngoại tiếp $\triangle DMN$, em nghĩ cần nói thêm là “vì $\triangle DMN = \triangle ABC$ nên chúng có cùng bán kính đường tròn nội tiếp” nữa.

Cho $G = \left\langle g \right\rangle \cong \mathbb{Z}$ là nhóm cyclic vô hạn. Ký hiệu $\text{Ext}^n_{\mathbb{C}G}(-,-)$ chỉ hàm tử $\text{Ext}^n$ trong phạm trù các biểu diễn phức hữu hạn chiều của $G$. Liệu ta có $\text{Ext}^n_{\mathbb{C}G}(\mathbb{C},V) = 0$ với mọi biểu diễn $V$ và mọi $n \ge 2$?

Chú ý: đây có thể coi như họ hàng xa của tính chất: nhóm hầu cyclic $\hat{\mathbb{Z}}$ có số chiều đối đồng điều (cohomological dimension) bằng 1.

Nếu muốn dùng véctơ thì có thể làm như sau: Gọi $a, b, c$ lần lượt là độ dài của $BC, CA, AB$. Ta có $$\overrightarrow{BE} = \frac{a}{c}\overrightarrow{BA} = \frac{a}{c}\overrightarrow{IA} - \frac{a}{c}\overrightarrow{IB}$$ và $$a\overrightarrow{IA} = -(b\overrightarrow{IB} + c\overrightarrow{IC}),$$ nên $$\overrightarrow{BE} = -\frac{1}{c}\left(b\overrightarrow{IB}+c\overrightarrow{IC}\right) - \frac{a}{c}\overrightarrow{IB} = -\frac{a+b}{c}\overrightarrow{IB} - \overrightarrow{IC}.$$ Từ đó ta có $$\overrightarrow{IE} = \overrightarrow{IB} + \overrightarrow{BE} = -\frac{a+b-c}{c}\overrightarrow{IB} - \overrightarrow{IC},$$ và tương tự, $$\overrightarrow{IF} = -\overrightarrow{IB} - \frac{a+c-b}{b}\overrightarrow{IC}.$$

Ta sẽ chứng minh rằng $$\frac{a+b-c}{c} = \frac{b}{a+c-b}.$$ Thật vậy, ta có các biến đổi tương đương $$\frac{a+b-c}{c} = \frac{b}{a+c-b} \Leftrightarrow (a+b-c)(a+c-b) = bc \Leftrightarrow a^2 = b^2 + c^2 - bc,$$ đẳng thức cuối cùng đúng theo định lý hàm số cosine (với chú ý rằng $\cos\widehat{BAC} = \cos 60^\circ = \frac{1}{2}$). Từ đó ta có $\overrightarrow{IE} = \frac{a+b-c}{c}\overrightarrow{IF}$, suy ra các véctơ $\overrightarrow{IE}$ và $\overrightarrow{IF}$ cùng phương.

Có ai dùng vecto để chứng minh thẳng hàng không ạ, sử dụng bổ đề: $a.\underset{IA}{\rightarrow}+b.\underset{IB}{\rightarrow}+c.\underset{IC}{\rightarrow}=\underset{0}{\rightarrow}$.

vì sao E(FD,IC)=-1 vậy ạ

Trường hợp $\triangle ABC$ cân tại $A$ thì hiển nhiên. Nếu không, bạn có thể gọi $D’$ là giao điểm của $EF$ và $BC$ rồi áp dụng Ceva và Menelaus để thấy $(D’D, BC) = -1$.

\begin{align*} \frac{\sqrt[3]{\cos 2x} - \sqrt{\cos x}}{\ln(1 - x^2)} & = \left(\frac{\sqrt[3]{\cos 2x} - 1}{x^2} - \frac{\sqrt{\cos x} - 1}{x^2}\right) \cdot \frac{x^2}{\ln(1 - x^2)} \\ & = \left(\frac{\cos 2x - 1}{\sqrt[3]{\cos^2 2x} + \sqrt[3]{\cos 2x} + 1} \cdot \frac{1}{x^2} - \frac{\cos x - 1}{\sqrt{\cos x} + 1} \cdot \frac{1}{x^2}\right) \cdot  \left(- \frac{\ln(1 - x^2)}{-x^2} \right)^{-1} \\ & = \left(\frac{\cos 2x - 1}{(2x)^2} \cdot \frac{4}{\sqrt[3]{\cos^2 2x} + \sqrt[3]{\cos 2x} + 1} - \frac{\cos x - 1}{x^2} \cdot \frac{1}{\sqrt{\cos x} + 1}\right) \cdot  \left(- \frac{\ln(1 - x^2)}{-x^2} \right)^{-1} \end{align*}

 

Sử dụng các giới hạn cơ bản $$\lim_{x \to 0} \frac{\cos x - 1}{x^2} = \frac{1}{2}, \quad \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1,$$ ta thu được $$I = \left(\frac{1}{2}\cdot\frac{4}{1+1+1} - \frac{1}{2} \cdot \frac{1}{1+1}\right) \cdot (-1)^{-1} = -\frac{5}{12}.$$

 

Mình đổi lại tên tâm đường tròn Euler của $\triangle ABC$ là $E$.

 

Cách làm bằng véctơ:

Gọi $I, J$ lần lượt là chân đường cao kẻ từ $B$ và từ $C$ của $\triangle ABC$. Gọi $P, Q, R, K$ lần lượt là trung điểm của $AB, AC, BC, IJ$. Gọi $G$ là trọng tâm $\triangle ABC$.

Ta có $$\overrightarrow{AT} = \overrightarrow{AE} + \overrightarrow{ET} = \frac{1}{2}(\overrightarrow{AO} + \overrightarrow{AH}) + (\overrightarrow{EM} + \overrightarrow{EN})$$ vì $E$ là trung điểm của $OH$, và vì tứ giác $EMTN$ là hình bình hành).

Một mặt, ta có tính chất quen thuộc $\overrightarrow{AH} = 2\overrightarrow{OR}$.

Mặt khác, đường thẳng $EM$ chứa đường trung bình của hình thang $HOPI$ và $M$ đối xứng với $E$ nên $\overrightarrow{EM} = \overrightarrow{OP} + \overrightarrow{HI}$. Tương tự, ta có $\overrightarrow{EN} = \overrightarrow{OQ} + \overrightarrow{HJ}$. Từ đó $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + (\overrightarrow{OR} + \overrightarrow{OP} + \overrightarrow{OQ}) + (\overrightarrow{HI} + \overrightarrow{HJ}).$$ Do $G$ cũng là trọng tâm của $\triangle PQR$ và do $K$ là trung điểm của $IJ$ nên $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + 3\overrightarrow{OG} + 2\overrightarrow{HK}.$$ Cuối cùng, $$3\overrightarrow{OG} = \overrightarrow{OH} = 2\overrightarrow{EH}$$ nên $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + 2\overrightarrow{EH} + 2\overrightarrow{HK} = \frac{1}{2}\overrightarrow{AO} + 2\overrightarrow{EK}.$$ Vì $EI = EJ$ nên đường thẳng $EK$ chính là đường trung trực của $IJ$, suy ra $EK \perp IJ$. Bằng tính chất quen thuộc rằng $IJ \perp AO$ (chứng minh chẳng hạn bằng cách cộng góc), ra suy ra $EK \parallel AO$, do đó các véctơ $\overrightarrow{AT}$ và $\overrightarrow{AO}$ cùng phương, hay $A, T, O$ thẳng hàng.

 

Thử chứng minh $$8(ab+bc+ca)(a^2 + b^2 + c^2) \ge 3(a+b+c)(a+b)(b+c)(c+a)$$ và thấy nó đúng thật . Khi nhân hết ra thì ta cần chứng minh $$5 \sum a^3 b + 5 \sum ab^3 \ge 6 \sum a^2 b^2 + 4abc \sum a,$$ trong đó $\sum$ chỉ tổng hoán vị vòng quanh. Từ đây áp dụng AM-GM: $$3a^3b + 3ab^3 \ge 6a^2 b^2$$ và $$\frac{4}{3}(a^3b + a^3b + bc^3) \ge 4a^2bc,$$ rồi cộng các bất đẳng thức tương tự lại là được. Cuối cùng ta có $$a+b+c \ge 3\sqrt[3]{\frac{a+b}{2} \cdot \frac{b+c}{2} \cdot \frac{c+a}{2}} = 3$$ theo bất đẳng thức AM-GM.

Cuối tháng 5 vừa rồi, ở hội nghị AGAG ở Charlottesville (https://sites.google...gag-at-uva/home), một bạn đồng nghiệp đã hỏi mình rằng nếu muốn nghiên cứu về vấn đề nguyên lý địa phương-toàn cục (nguyên lý Hasse) và tính chất xấp xỉ yếu cho đa tạp đại số trên trường số, thì nên bắt đầu từ đâu. Mình nghĩ sẽ có ích, nên mình sẽ đăng lại email trả lời của mình (tiếng Anh ở dưới):

 

Rất vui được gặp bạn hôm nay ở Charlottesville. Vì bạn đã hỏi một số tài liệu tham khảo về nguyên lý Hasse và tính chất xấp xỉ yếu để bắt đầu tìm hiểu, tôi viết thư cho bạn hòng trả lời câu hỏi đó. Dưới đây là "túi khôn" của những những người trong cùng trường phái với tôi.

Trước hết, bạn cần làm quen với đối đồng điều Galois, lý thuyết trường các lớp và các định lý đối ngẫu số học (đối ngẫu địa phương Tate và đối ngẫu toàn cục Poitou-Tate. Tài liệu tham khảo điển hình cho chủ đề này là ghi chú "Arithmetic Duality Theorems" (miễn phí) của James S. Milne, hoặc cuốn sách của Harari mà bản tiếng Anh có tựa là "Galois Cohomology and Class Field Theory".

Cuốn sách "gối đầu giường" có lẽ là "Torsors and Rational Points" của Skorobogatov. Trở ngại Brauer-Manin, torsors trong hình học số... được giải thích một cách khá chi tiết trong đó. Bạn cũng có thể xem cuốn sách mới xuất bản của Colliot-Thélène và Skorobogatov là "The Brauer-Grothendieck Group".

Đối với các tính chất số học của nhóm đại số tuyến tính, tôi đề xuất cuốn sách của Platonov và Rapinchuk là "Algebraic Group and Number Theory", cũng như bài báo mang tính nền tảng của Sansuc, "Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres" (sẽ rất tuyệt nếu bạn đọc được tiếng Pháp, đây là một bài báo xuất sắc).

Lý thuyết xuống thang (descent) là một từ khóa khác. Hãy xem hai bài báo "La descente sur les variétés rationnelles I" và "... II" của Colliot-Thélène và Sansuc. Lý thuyết này cũng xuất hiện trong sách của Skorobogatov. Ở một thái cực khác, người ta nói về phương pháp phân thớ (fibration). Bạn có thể xem xét việc đọc nó từ luận án của Harari là "Méthode des fibrations et obstruction de Manin". Bạn không nhất thiết phải hiểu chính xác toàn bộ chi tiết ở lần đọc đầu tiên, vì chúng thực sự rất kỹ thuật.

Nâng cao hơn, bạn có thể đọc các bài báo của Borovoi là "Abelian cohomology of reductive group" và "The Brauer-Manin obstructions for homogeneous spaces with connected or abelian stabilizer". Chúng minh họa một cơ chế tổng quát là "abel hóa đối đồng điều Galois không giao hóa", rất ngạc nhiên là cơ chế này vận hành rất tốt khi làm việc với nhóm đại số tuyến tính liên thông. Bạn cũng có thể cần biết một chút về H^2 không giao hoán: xem bài báo "Grothendieck's theorem on non-abelian H^2 and local-global principles" của Flicker, Schreiderer và Sujatha.
 

It was nice to have met you today in Charlottesville. Since you have asked for some references on the Hasse principle and weak approximation to start with, I am writing to you in an attempt to give you an answer. Here is the bag of tricks of people from the same school as mine.

First, you should get yourself familiar with Galois cohomology, class field theory, and arithmetic duality theorems (Tate local duality and Poitou-Tate global duality). Typical references for this topic are James S Milne's free notes "Arithmetic Duality Theorems", or Harari's textbook, whose English version has the title "Galois Cohomology and Class Field Theory".

The bedside book should be Skorobogatov's textbook "Torsors and Rational Points". Brauer-Manin obstruction, torsors in arithmetic geometry... are explained pretty thoroughly there. You can also take a look at Colliot-Thélène and Skorobogatov's recent textbook "The Brauer-Grothendieck Group".

As for arithmetics of linear algebraic groups, I recommend Platonov and Rapinchuk's textbook "Algebraic Group and Number Theory", as well as the fundamental paper of Sansuc, "Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres" (it would be fantastic if you could read French, this is a formidable article).

"Descent theory" is another keyword. Take a look at Colliot-Thélène and Sansuc's papers "La descente sur les variétés rationnelles I" and  "... II". This also appears in Skorobogatov's textbook. On the other extreme, one talks about the "fibration method". You should consider learning its ideas from Harari's thesis "Méthode des fibrations et obstruction de Manin". It is not really necessary to understand all the details in the first lecture since they are very technical.

For advanced readings, you can take a look at Borovoi's papers "Abelian cohomology of reductive groups" and "The Brauer-Manin obstructions for homogeneous spaces with connected or abelian stabilizer". They illustrate the general machinery of "abelianization of non-abelian Galois cohomology", which works surprisingly well for connected linear algebraic groups. You might also need to know a bit about non-abelian H^2: see Flicker, Schreiderer and Sujatha's paper "Grothendieck's theorem on non-abelian H^2 and local-global principles".

mặt cầu có độ cong dương nên không trải phẳng như mặt trụ hay mặt nón được nhé

Bài giảng số học - Đặng Hùng Thắng

Với $G$ là một nhóm, nhắc lại rằng giao hoán tử của hai phần tử $x,y \in G$ được định nghĩa bởi $[x,y]:=xyx^{-1}y^{-1}$. Nhóm con dẫn xuất của $G$, ký hiệu bởi $[G,G]$, được định nghĩa là nhóm con sinh bởi tất cả các giao hoán tử $[x,y]$, với $x,y \in G$; đây là một nhóm con chuẩn tắc của $G$. Abel hóa của $G$ là nhóm thương $G^{\text{ab}}:=G/[G,G]$; đây là một nhóm abel.

 

Nếu $G$ tác động trên một nhóm abel $A$ (bởi các tự đẳng cấu nhóm, tất nhiên), với tác động ký hiệu bởi $G \times A \owns (g,a) \mapsto g  \cdot a \in A$, ta gọi đối bất biến $A_G$ của $A$ là nhóm thương của $A$ bởi nhóm con sinh bởi các phần tử $g \cdot a - a$, với $g \in G$ và $a \in A$.

 

Nếu $G$ tác động lên một nhóm $H$ (bởi các tự đẳng cấu nhóm), tích nửa trực tiếp $H \rtimes G$ là tích Descartes $H \times G$ với phép nhân cho bởi công thức $(h_1,g_1)(h_2,g_2) := (h_1(g_1 \cdot h_2), g_1g_2)$.

Chứng minh rằng khi đó, tác động của $G$ trên $H$ cảm sinh một tác động trên $H^{\text{ab}}$, và abel hóa của $H \rtimes G$ được cho bởi công thức $$(H \rtimes G)^{\text{ab}} = H^{\text{ab}}_G \times G^{\text{ab}}.$$

Với $n=0$, bài toán không có nghiệm.
Với $n=1$, hiển nhiên tất cả các nghiệm cho bởi $(P(x), Q(x)) = (x-a, x-a-1)$, với $a$ là số nguyên dương tuỳ ý.
Xét $n \ge 2$. Viết $Q(x) = (x-a_1)\cdots (x-a_n)$ với $a_1 \le \cdots \le a_n$ là các số tự nhiên. Nếu $a$ là một nghiệm của $P$ thì $(a-a_1)\cdots (a-a_n) = Q(a) = P(a) - 1 = -1$, suy ra $a-a_i \in \{\pm 1\}$ với mọi $i = 1,\ldots,n$. Mặt khác ta không thể có $a-a_1 = \cdots = a-a_n = 1$, nên tồn tại chỉ số $i$ sao cho $a-a_i = -1$. Mà $a-a_1 \ge \cdots \ge a-a_n$ nên $a-a_n = -1$, hay $a = a_n - 1$, nghĩa là đây là nghiệm duy nhấy của $P$. Vậy $P(x) = (x-a)^n$.
Ta cũng có $Q(x) = (x-a+1)^k (x-a-1)^{n-k}$ với $0 \le k < n$ nào đó. Nếu $n \ge 3$ thì $k \ge 2$ hoặc $n-k \ge 2$. Trong trường hợp thứ nhất thì $Q’(a-1) = 0$, trong trường hợp thứ hai thì $Q’(a+1) = 0$. Nhưng $Q’(x) = P’(x) = n(x-a)^{n-1}$ chỉ có nghiệm duy nhất là $a$, mâu thuẫn. Vậy với $n \ge 3$ thì bài toán không có nghiệm.
Ta chỉ còn trường hợp $n = 2$. Lúc này, thử trực tiếp $k = 0$ và $k = 1$, ta thấy tất cả các nghiệm của bài toán là $(P(x), Q(x)) = ((x-a)^2, (x-a+1)(x-a-1))$, với $a$ là số nguyên dương tuỳ ý.