em nhận áo r :v bọn trong lớp thấy áo đẹp gato lắm :v :v

Cho a;b;c là các số thực thỏa mãn điều kiện a;b lớn hơn 0 và 19a+6b+9c=12

CMR ít nhất 1 trong 2 phương trình sau có nghiệm : 

  $x^{2}-2(a+1)x+a^{2}+6abc+1=0$ và $x^{2}-2(b+1)x+b^{2}+19abc+1=0$

Ta có $\Delta {'_1} = a\left( {2 - 6bc} \right)$, $\Delta {'_2} = b\left( {2 - 19ac} \right)$.

Mà $\left( {2 - 6bc} \right) + \left( {2 - 19ac} \right) = 4 - c\left( {19a + 6b} \right) = 4 - c\left( {12 - 9c} \right) = {\left( {3c - 2} \right)^2} \ge 0$

Do đó ít nhất một trong hai số ${2 - 19ac}$, ${2 - 6bc}$ không âm.

Ta lại có $a \ge 0$, $b \ge 0$ nên ít nhất một trong hai số $\Delta {'_1}$, $\Delta {'_2}$ không âm.

Từ đó có đpcm.

 $2(x^2-x+6)=5 \sqrt{x^3+8}$

ĐK: $x \ge  - 2$

Đặt $a = x + 2$, $b = x^2 - 2x + 4$ ta có $2\left( {a + b} \right) = 5\sqrt {ab}  \Leftrightarrow 4{\left( {a + b} \right)^2} = 25ab \Leftrightarrow \left( {4a - b} \right)\left( {a - 4b} \right) = 0$

$ \Leftrightarrow a = \frac{1}{4}b \vee a = 4b$

Tới đây dễ rồi :v

Bài 3:

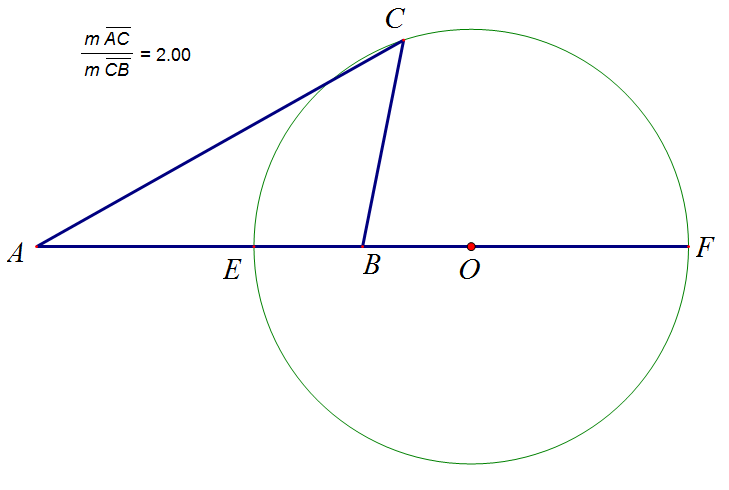
2. Cho $\Delta ABC$ thay đổi có $AB=6$,$AC=2BC$.Tìm giá trị lớn nhất của diện tích $\Delta ABC$.

Gọi $E$, $F$ : điểm chia trong, chia ngoài đoạn $AB$ theo tỉ số $2$ $ \Rightarrow EB = 2$, $BF=6$.

Ta có $(O; OE=4)$ là đường tròn Apollonius xác định bởi đoạn $AB$ và số $2$ và $C \in (O)$ (với O : trung điểm EF).

Khi đó ${S_{ABC}} \le \frac{1}{2}.6.4 = 12$.

Đẳng thức xảy ra khi $C$ là điểm chính giữa cung $EF$ của $(O)$.

Bài 1:Cho $a,b,c$ là các số thực dương thỏa mãn $a^3+b^3+c^3-3abc=1$ .Tìm $minP=a^2+b^2+c^2 $

Bài 2: Cho $a,b,c,d$ thỏa mãn $a> b> c> d$ và $ac+bd=(b+d+a-c)(b+d-a+c)$ . Chứng minh $ab+cd$ là hợp số

Bài 3:

1. Tìm hai số nguyên dương $a$ và $b$ thỏa mãn $a^2+b^2=[a,b]+7(a,b)$(với $[a,b]=BCNN(a,b); (a,b)=UCLN(a,b)$)

2. Cho $\Delta ABC$ thay đổi có $AB=6$,$AC=2BC$.Tìm giá trị lớn nhất của diện tích $\Delta ABC$.

Bài 4: Cho $a,b,c$ là các số nguyên tố thỏa mãn: $20abc<30(a+b+c)<21abc$. Tìm $a,b,c$.

Bài 1.

$1 = {\left( {{a^3} + {b^3} + {c^3} - 3abc} \right)^2} = {\left( {a + b + c} \right)^2}{\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right)^2}\mathop  \le \limits^{AM - GM} {\left[ {\frac{{{{\left( {a + b + c} \right)}^2} + 2\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right)}}{3}} \right]^3} = {\left( {{a^2} + {b^2} + {c^2}} \right)^3}$

$ \Rightarrow P \ge 1$

Đẳng thức xảy ra $ \Leftrightarrow \left( {a{\rm{, }}b{\rm{, }}c} \right) = \left( {0{\rm{; }}0{\rm{; }}1} \right)$ và hoán vị.

     Cho tam giác ABC nhọn AB<AC. Hai đường cao BD và CE cắt nhau tại H. I là trung điểm của BC. Đường tròn đi qua ba điểm B,E,I và đường tròn đi qua ba điểm C,D,I cắt nhau tại K khác I. Chứng minh

rằng:

     a) A,E,H,K,D thuộc một đường tròn và góc BDK bằng góc CEK

     b)  Biết DE cắt BC tại M. Chứng minh rằng ba điểm M,H,K thẳng hàng.

a) $\widehat {AEH} = \widehat {ADH} = 90^\circ  \Rightarrow ADHE$ nội tiếp.

Ta có : $\widehat {AEK} + \widehat {ADK} = \widehat {KIB} + \widehat {KIC} = 180^\circ  \Rightarrow ADKE$ nội tiếp.

Vậy : $A$, $E$, $H$, $K$, $D$ cùng thuộc đường tròn đường kính $AH$.

Từ đó : $\widehat {BDK} = \widehat {CEK}$ (do cùng chắn cung $HK$).

b) Do tứ giác $DCIK$ nội tiếp nên $\widehat {ADK} = \widehat {KIC}$.

Ta có : $\widehat {AKD} = \widehat {AHD} = \widehat C = \widehat {CDI} = \widehat {CKI}$.

Do đó : $\Delta ADK$ đồng dạng với $\Delta CIK$ (g - g) $ \Rightarrow \widehat {KCM} = \widehat {DAK} = \widehat {DEK} \Rightarrow CMEK$ nội tiếp.

Suy ra : $\widehat {EKM} = \widehat {ECB}$.

Ta lại có : $\widehat {EKH} = \widehat {EAH}$.

Mà $\widehat {EAH} = \widehat {ECB}$ nên $\widehat {EKH} = \widehat {EKM}$.

Vậy ta có đpcm.

Cho x,y,z >0 thỏa xy + yz +zx =xyz chứng minh $\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\geq \sqrt{xyz}+\sqrt{x}+\sqrt{y}+\sqrt{z}$

$VT = \sum {\sqrt {x + yz} }  = \sum {\sqrt {\frac{{{x^2} + xyz}}{x}} }  = \sum {\sqrt {\frac{{{x^2} + xy + yz + zx}}{x}} } $

$VT = \sum {\sqrt {\frac{{\left( {x + y} \right)\left( {x + z} \right)}}{x}} } \mathop  \ge \limits^{B.C.S} \sum {\frac{{x + \sqrt {yz} }}{{\sqrt x }}}  = \sum {\left( {\sqrt x  + \sqrt {\frac{{yz}}{x}} } \right)} $

Mà $\sum {\sqrt {\frac{{yz}}{x}}  = \frac{{xy + yz + zx}}{{\sqrt {xyz} }} = \sqrt {xyz} } $

Vậy ta có đpcm.

Tìm số tự nhiên a,b,c thỏa mãn $\overline{abc}= 11(a^2 +b^2 +c^2)$

Ta có $100 \ge 11(a^2+b^2+c^2) \le 999$ 
Suy ra $9 \le a^2+b^2+c^2 \le 90$ 
Giả sử $a \ge b \ge c$  
$90 \ge \sum a^2 \ge 3c^2$  và $9 \le a^2+b^2+c^2 \le 3a^2$ 
$\rightarrow 5 \ge c$ và $
Mà ta có $a+c-b \vdots 11$
Đến đây bạn tự xét trường hợp nhé . Có ai có cách ngắn hơn ko ?

Vai trò của $a$, $b$, $c$ không như nhau nên không giả sử được đâu bạn.

Ta có : $11\left( {{a^2} + {b^2} + {c^2}} \right) = \overline {abc}  = 100a + 10b + c \Leftrightarrow 99a + 11b + \left( {a - b + c} \right) = 11\left( {{a^2} + {b^2} + {c^2}} \right)$ $(1)$.

Vì $a - b + c \vdots 11$ và $ - 8 \le a - b + c \le 18$ nên ta có $2$ trường hợp :

Trường hợp 1 : $a - b + c = 0$ : $(1) \Rightarrow 9a + b = {a^2} + {b^2} + {c^2}$ $(2)$.

Thay $b=a+c$ :

$10a + c = 2\left( {{a^2} + ac + {c^2}} \right) \Leftrightarrow c = 2\left[ {a\left( {a - 5} \right) + c\left( {a + c} \right)} \right]$

Ta có $c \vdots 2 \Rightarrow a\left( {a - 5} \right) + c\left( {a + c} \right) \vdots 2 \Rightarrow c \vdots 4$.

Nếu $c = 0$ : thay vào $(2)$ tìm $a$, rồi suy ra $b$ ta được $\overline {abc}  = 550$.

Nếu $c \ne 0$ : $(2) \Rightarrow 10a = 2{a^2} + 2ac + c\left( {2c - 1} \right) > 2{a^2} + 2ac = 2ab \Rightarrow 5 > b > c \Rightarrow c \le 3$ (loại).

Trường hợp 2 : $a - b + c = 11$ : $(1) \Rightarrow 9a + b + 1 = {a^2} + {b^2} + {c^2}$ $(3)$.

Thay $b = a + c - 11$ :

$10a + c - 10 = 2\left( {{a^2} + {c^2} + ac - 11a - 11c} \right) + 121$

$\Leftrightarrow c = 2\left[ {a\left( {a - 11} \right) + c\left( {c - 11} \right) + a\left( {c - 5} \right) + 131} \right]$.

Lúc này $c$ lẻ nên $a\left( {a - 11} \right) + c\left( {c - 11} \right) + a\left( {c - 5} \right) \vdots 2 \Rightarrow c + 1 \vdots 4 \Rightarrow c = 3 \vee c = 7$.

Nếu $c=7$ : $(3) \Rightarrow {a^2} - 9a + 34 = 0$ (vô nghiệm).

Nếu $c=3$ : $(3) \Rightarrow {a^2} - 13a + 40 = 0 \Rightarrow a = 5 \vee a = 8$.

Mà $a = b - c + 11 = b + 8 \ge 8$ nên $a=8 \Rightarrow \overline {abc}  = 803$.

Vậy có $2$ số cần tìm là $550$, $803$.

Bạn giải thích giúp mình chỗ kia kĩ hơn đc k

đấy là phương tích trong đường tròn thôi :v có thể chứng minh bằng tam giác đồng dạng $\Delta MDC ~ \Delta MCB$ (g - g) :v

Cho đường tròn tâ $O$, từ $A$ nằm ngoài đường tròn, kẻ hai tiếp tuyến $AB;AC$ với $B;C$ là các tiếp điểm. Gọi $M$ là trung điểm $AC$, $BM \cap (O) = D \ne B$, $AD \cap (O) =E \ne D$. Chứng minh rằng $BE \| AC$

Ta có : $AM^2 = MC^2 = MD.MB \Rightarrow \frac{AM}{MD} = \frac{MB}{AM} \Rightarrow \Delta AMD ~ \Delta BMA$ (c - g - c)

$\Rightarrow \widehat{DAM} = \widehat{ABM} = \widehat{AEB}$ (đpcm).

cho tam giác ABC vuông ở A, có góc B = 20 Độ, vẽ phân giác trong BI, vẽ góc ACH = 30 Độ về phía trong tam giác ( H năm trên AB) 
Tính góc CHI

Ta có : $\widehat{ACB}=70^{\circ} \Rightarrow \widehat{HCB}=40^{\circ}$.

Vẽ phân giác $CK$ của $\widehat{HCB}$ thì $\widehat{HCK}=\widehat{BCK}=20^{\circ}=\widehat{B} \Rightarrow \Delta KBC$ cân tại $K$.

Kẻ $KM \perp BC$ thì $M$ là trung điểm $BC$.

Ta có : $\Delta BMK ~ \Delta BAC$ (g - g) $\Rightarrow \frac{AB}{BC} = \frac{MB}{BK} = \frac{BC}{2BK}$. $(1)$

$\Delta AHC$ vuông có $\widehat{ACH} = 30^{\circ}$ nên $AH = \frac{1}{2}CH \Rightarrow \frac{AH}{HK} = \frac{CH}{2HK} = \frac{BC}{2BK}$. $(2)$

$\frac{AB}{BC} = \frac{AI}{IC}$. $(3)$

Từ $(1)$, $(2)$, $(3)$ $\Rightarrow \frac{AH}{HK} = \frac{AI}{IC} \Rightarrow HI \parallel CK \Rightarrow \widehat{CHI} = \widehat{HCK} = 20^{\circ}$.

Cho x,y,z,t $\geqslant$ 0 và $x^{2} + y^{2} + z^{2} + t^{2} = 2005$

C/m: $\frac{x}{2005\sqrt{2005}+yzt} + \frac{y}{2005\sqrt{2005}+xzt} + \frac{z}{2005\sqrt{2005}+xyt} + \frac{t}{2005\sqrt{2005}+xyz} \geq \frac{1}{2005}$

Đặt $a=\frac{x}{\sqrt{2005}}$, $b=\frac{y}{\sqrt{2005}}$, $c=\frac{z}{\sqrt{2005}}$, $d=\frac{t}{\sqrt{2005}}$.

Ta có $a,b,c,d\geq 0\wedge a^2+b^2+c^2+d^2=1$ (1).

$A=\frac{x}{2005\sqrt{2005}+yzt}+\frac{y}{2005\sqrt{2005}+ztx}+\frac{z}{2005\sqrt{2005}+txy}+\frac{t}{2005\sqrt{2005}+xyz}=\frac{1}{2005}\left ( \frac{a}{1+bcd}+\frac{b}{1+acd}+\frac{c}{1+abd}+\frac{d}{1+abc} \right )$

$A\geq \frac{1}{2005}.\frac{\left ( a+b+c+d \right )^2}{a\left ( 1+bcd \right )+b\left ( 1+acd \right )+c\left ( 1+abd \right )+d\left ( 1+abc \right )}=\frac{1+2\left ( ab+ac+ad+bc+bd+cd \right )}{2005 \left(a+b+c+d+4abcd \right)}$

Do đó cần chứng minh $\frac{1+2\left ( ab+ac+ad+bc+bd+cd \right )}{a+b+c+d+4abcd}\geq 1 \Leftrightarrow 1+2\left ( ab+ac+ad+bc+bd+cd \right )\geq a+b+c+d+4abcd$.

Thật vậy, (1) $\Rightarrow a,b,c,d\in [0,1]$

Ta có $VT-VP=\left ( 1-a \right )\left ( 1-b \right )\left ( 1-c \right )\left ( 1-d \right )+\left ( ab+ac+ad+bc+bd+cd \right )+\left ( abc+abd+acd+bcd \right )-5abcd\geq ab+ac+ad+bc+bd+cd-5abcd\geq 6\sqrt[6]{a^3b^3c^3d^3}-5abcd=5\sqrt{abcd}\left ( 1-\sqrt{abcd} \right )+\sqrt{abcd}\geq 0$.

Vậy bất đẳng thức được chứng minh.

Đẳng thức xảy ra $\Leftrightarrow (a,b,c,d)=(0,0,0,1)$ và các hoán vị $\Leftrightarrow (x,y,z,t)=(0,0,0,\sqrt{2005})$ và các hoán vị.

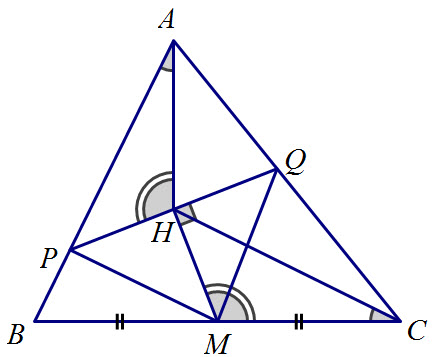
Cho tam giác ABC nhọn, trực tâm H. Gọi M là trung điểm BC. Đường thẳng qua H và vuông góc với MH cắt AB, AC lần lượt tại P và Q. 

CMR: tam giác MPQ cân. 

Chứng minh được $\Delta AHP ~ \Delta CMH$ (g - g) $\Rightarrow \frac{HP}{MH}=\frac{AH}{MC}$.

Tương tự, $\frac{HQ}{MH}=\frac{AH}{MB}$.

Suy ra $HP=HQ$. Từ đó $\Delta MPQ$ cân tại $M$.

Tìm x:

$\dfrac{(2009-x)^2+(2009-x)(x-2010)+(x-2010)^2}{(2009-x)^2-(2009-x)(x-2010)+(x-2010)^2}=\dfrac{19}{49}$

Đặt $a=2009-x$, $b=x-2010$ $\Rightarrow a+b=-1$.

Ta có : $\frac{19}{49}=\frac{a^2+ab+b^2}{a^2-ab+b^2}=\frac{\left ( a+b \right )^2-ab}{\left ( a+b \right )^2-3ab}=\frac{1-ab}{1-3ab}$ $\Rightarrow ab=-3\tfrac{3}{4}$.

Từ đó tính được $a$ hoặc $b$, suy ra $x$.

Má ơi Mozilla nhà tôi bị làm sao ấy không vào được ai gặp trường hợp này chưa?

nói lời tạm biệt fb đi =))

Anh em cho hỏi bao giờ thì mình load được FB nhỉ?

do ăn ở đó =))) mình vào bình thường =))

Giải phương trình :

$$\dfrac{1}{x} + \dfrac{1}{x+2} + \dfrac{1}{x+5} + \dfrac{1}{x+7} = \dfrac{1}{x+1} + \dfrac{1}{x+3} + \dfrac{1}{x+4} + \dfrac{1}{x+6}$$

$\left ( \frac{1}{x}+\frac{1}{x+7} \right )+\left ( \frac{1}{x+2}+\frac{1}{x+5} \right )=\left ( \frac{1}{x+1}+\frac{1}{x+6} \right )+\left ( \frac{1}{x+3}+\frac{1}{x+4} \right )$

$\Leftrightarrow \frac{2x+7}{x^2+7x}+\frac{2x+7}{x^2+7x+10}=\frac{2x+7}{x^2+7x+6}+\frac{2x+7}{x^2+7x+12}$

$\Leftrightarrow \left ( 2x+7 \right )\left ( \frac{1}{y}+\frac{1}{y+10}-\frac{1}{y+6}-\frac{1}{y+12}\right )=0$ (với $y=x^2+7x$)

Phương trình $2x+7=0$ có nghiệm $x=-\frac{7}{2}$.

$\left ( \frac{1}{y}-\frac{1}{y+6} \right )+\left ( \frac{1}{y+10}-\frac{1}{y+12} \right )=0$ $\Leftrightarrow \frac{6}{y^2+6y}+\frac{2}{y^2+22y+120}=0$ $\Leftrightarrow y^2+18y+90=0$, vô nghiệm

Vậy $x=-\frac{7}{2}$.

sắp vào học rồi :'(

Bài 3: Cho hình chữ nhật ABCD,có AB=14, BC=6; M,N,P,Q thuộc các cạnh AB, BC, CD, AD sao cho AM=AQ=Cn=CP=x (6>x>0)

a) Xác định x để từ giác MNPQ có diện tích lớn nhất 

b) Xác định x đề tứ giác MNPQ là hình thoi

Ta có $MNPQ$ là hình bình hành.

a) $(S_{MNPQ})_{max} \Leftrightarrow (2S_{AMQ}+2S_{MBN})_{min}$

Ta có : $2S_{AMQ}+2S_{MBN}=AM^2+MB.BN=x^2+\left ( 14-x \right )\left ( 6-x \right )=2\left ( x^2-10x+42 \right )=2\left ( x-5 \right )^2+34\geq 34$

Do đó $S_{MNPQ}\leq 50$ đvdt

Đẳng thức xảy ra khi $x=5$.

b) $MNPQ$ là hình thoi $\Leftrightarrow MQ=MN \Leftrightarrow MQ^2=MN^2 \Leftrightarrow 2.AM^2=MB^2+BN^2 \Leftrightarrow 2x^2=\left ( 14-x \right )^2+\left ( 6-x \right )^2 \Leftrightarrow x=5\tfrac{4}{5}$.

Bài 4: Cho $\Delta$ABC nhọn, H là trực tâm. Qua H vẽ một đường thẳng cắt AB, AC lần lượt tại D, E sao cho HD=HE. Qua H vẽ đường thẳng khác vuông góc DE cắt BC tại M. Chứng minh:

a) $\frac{BM}{AH}=\frac{HM}{HE}$

b)M là trung điểm BC

a) Xét $\Delta BHM$ và $\Delta AEH$ có $\widehat{HBM}=\widehat{HAE}$ (vì cùng nhọn và $BH\perp AE$, $BM\perp AH$), $\widehat{BMH}=\widehat{AHE}$ (vì cùng nhọn và $BM\perp AH$, $MH\perp HE$)

$\Rightarrow \Delta BHM\sim \Delta AEH$ $(g-g)$ $\Rightarrow \frac{BM}{AH}=\frac{HM}{HE}$ (đpcm).

b) Chứng minh tương tự, ta cũng có $\frac{CM}{AH}=\frac{HM}{HD}$ $\Rightarrow \frac{BM}{AH}=\frac{CM}{AH}$ $\Rightarrow BM=CM$ (đpcm).

Tổ ngoại khóa Sinh vật của lớp em đã cưa một số ván mỏng thành những tấm hình chữ nhật để chuẫn bị làm khay đựng đồ mổ. Nếu không dùng êke, thước vuông, thước đo góc, compa v.v.. mà chỉ với sợi dây có sẵn trong tay, em có thể kiểm tra xem những tấm ấy có phải là hình chữ nhật được không ? Nếu được em hãy trình bày cách làm của em. Dựa vào đâu mà em có thể tin rằng cách làm ấy là đúng ?

dùng dây để đo & xác định các độ dài có bằng nhau không =))

đo lần lượt 2 cặp cạnh đối của ván, nếu có 1 cặp cạnh đối không bằng nhau thì xác định nó không phải rồi khỏi đo tiếp =))

nếu cả 2 cặp cạnh đối đều bằng nhau thì đo tiếp 2 đường chéo của nó ta sẽ có kết luận =))

KỆ CÔ     

em chỉ quan tâm chuyện bác béo & dâm thôi :3

Bác không nói em không bảo bác câm đâu   

kệ bác :3

Bác hát  bị ném đá à ,  em nói cũng bị ném đá cơ 

Chẳng là hồi ấy là mùa đông ( lớp 9 ạ) em bị viêm họng ( mà nói chung chỉ cần trời cứ hơi se lạnh thôi là em lại bị cái bệnh này - do hồi lớp 7 hay 8 j đó bị nặng quá phải nằm viện mà chưa không dứt điểm đâm ra giờ nó.............................    ) nên nói giọng nó khàn khàn mà hầu như không nghe được ( giống vịt đực ý     ). Mà em lại nói nhiều cơ nên mỗi lần em nói bọn nó lại " Thôi Chi ơi mày đừng có nói nữa " / " Chi ơi mày câm ngay cho tao " ....................  Thế là em tức em không thèm nói nữa. Đến lúc kiểm tra bọn nó hỏi bài em không trả lời, bọn nó bảo Chi ơi mày nhớ đấy. Em bảo ai bảo mày bảo tao không được nói mà    

Đáng đời bọn nó   

Thật ra là chuyện cũng chả có j đâu mà viết cho topic đỡ mốc   hề hề

bọn nó thật thông minh khi nói không với bác :3

3. Cho $a_{1};a_{2};a_{3};...;a_{n} \epsilon \begin{Bmatrix} -1;1 \end{Bmatrix}$ với mọi n nguyên dương thỏa $a_{1}a_{2}+a_{2}a_{3}+...+a_{n}a_{1}=0$. Chứng minh rằng n $\vdots 4$

Đặt $x_1=a_1a_2$, $x_2=a_2a_3$, $...$, $x_n=a_na_1$.

Khi đó $x_1$, $x_2$, $...$, $x_n \in \left \{ -1;1 \right \}$.

Lại có $x_1+x_2+...+x_n=0$ $\Rightarrow $ trong các số $x_1$, $x_2$, $...$, $x_n$ số giá trị $1$ bằng số giá trị $-1$.

Giả sử có $m$ giá trị $1$ và $m$ giá trị $-1$, với $m\in\mathbb{N^*} \Rightarrow n=2m$ và $x_1x_2...x_n=\left ( -1 \right )^m$

Mặt khác, $x_1x_2...x_n=\left ( a_1a_2...a_n \right )^2=1$ nên $m$ chẵn

Do đó $n\vdots 4$.