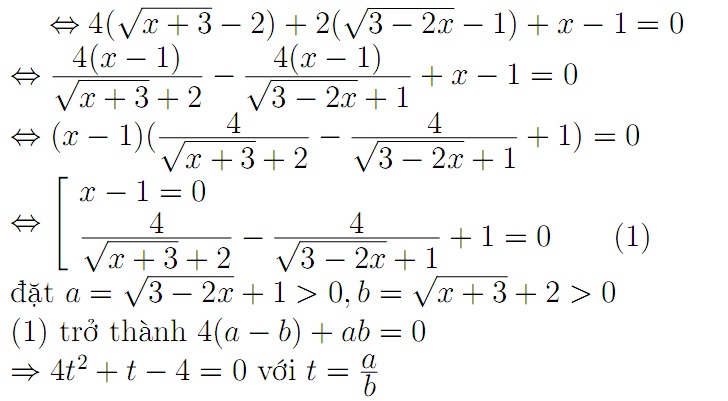analysis90 nội dung
Có 38 mục bởi analysis90 (Tìm giới hạn từ 02-05-2020)
#307504 Đề thi ôn tập thường xuyên của ĐHĐT
 Đã gửi bởi
analysis90
on 01-04-2012 - 12:13
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 01-04-2012 - 12:13
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
#306948 Đề thi ôn tập thường xuyên của ĐHĐT
 Đã gửi bởi
analysis90
on 30-03-2012 - 09:46
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 30-03-2012 - 09:46
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
MATHEMATICAL OLYMPIAD STUDENT
(third-2012)
Exercise 1. For $f(x)=2(x-1)-\arctan x,x\in\mathbb{R}$.a) Prove that $f(x)=0$ have only a root $a\in(1,\sqrt{3})$.
b) Let $\{u_{n}\}_{n=1}^{\infty}$ be a sequence defined by$\left\{\begin{matrix} u_1=\dfrac{3}{2}& \\ u_n=1+\dfrac{1}{2}\arctan x,&n\geq1 \end{matrix}\right.$.
Prove that $\{u_{n}\}_{n=1}^{\infty}$ converges to $a$.
Exercise 2. Let $f:[0,+\infty)\longrightarrow \mathbb{R}$ be a differentiable function such that $f(0)=1$. Prove that if $f'(x)\geq f(x)$ for all $x\in[0,+\infty)$, then the function $g(x)=f(x)-e^x$ is a increasing function.
Exercise 3. Let $f:[0,1]\longrightarrow \mathbb{R}$ be a integrable function such that $\int_0^1xf(x)dx=0$. Prove that
$\int_0^1f^2(x)dx\geq 4(\int_0^1f(x)dx)^2$.
Exercise 4. Let $f:\mathbb{R}\longrightarrow \mathbb{R}$ be a twice differentiable, $g:\mathbb{R}\longrightarrow \mathbb{R}^+$ be a function such that $f(x)+f''(x)=-xg(x)f'(x)$ for all $x\in\mathbb{R}$. Prove that $f(x)$ is bounded.
Exercise 5. Let $P(x)=\sum_{i=0}^{n}a_ix^i$ with $a_n>0$ be a $n$ degrees polynomial and have distinct $n$ roots. Prove that the polynomial $Q(x)=(P(x))^2-P'(x)$ only have
a) distinct $n+1$ roots if $n$ is odd.
b) distinct $n$ roots if $n$ is even.
Exercise 6. Find al function $f:\mathbb{R}\longrightarrow \mathbb{R}$ satisfies
$f(x+y)\geq f(x).f(y)\geq e^{x+y}$ for all $x,y\in \mathbb{R}$.
#304691 AB+BC+CA lớn nhất
 Đã gửi bởi
analysis90
on 16-03-2012 - 23:29
trong
Hình học
Đã gửi bởi
analysis90
on 16-03-2012 - 23:29
trong
Hình học
#303046 Ôn thi Olympic Toán học sinh viên 2015 [Giải tích]
 Đã gửi bởi
analysis90
on 09-03-2012 - 08:25
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 09-03-2012 - 08:25
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$e[f(1)-1]+1=g(1)<g(0)=0$
If $f(x)+f'(x)<1$ then there don't exist $f(x)$.
#302253 Đề thi chọn đội tuyển Olympic SV 2012 môn Giải tích - ĐHKHTN, ĐHQGHN
 Đã gửi bởi
analysis90
on 04-03-2012 - 22:03
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 04-03-2012 - 22:03
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$f(x)=f(x)-f(0)=f'(\theta_1)x,\theta_1\in(0,x)\geq-2x$
$f(x)-f(1)=f'(\theta_2)(x-1),\theta_2\in(x,1)\Rightarrow f(x)\geq 2x-1$.
So,
$\int_0^1f(x)dx=\int_0^\frac{1}{4}f(x)dx+\int_\frac{1}{4}^1f(x)dx
\geq \int_0^\frac{1}{4}-2xdx+\int_\frac{1}{4}^1 (2x-1)dx=\dfrac{1}{8}$
But $f(x)=\left\{\begin{matrix}
-2x &x\in[0,\frac{1}{4}] \\
2x-1&x\in[\frac{1}{4},1]
\end{matrix}\right.$
isn't continuous at $x=\dfrac{1}{4} $.
#302224 Đề thi chọn đội tuyển Olympic SV 2012 môn Giải tích - ĐHKHTN, ĐHQGHN
 Đã gửi bởi
analysis90
on 04-03-2012 - 20:38
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 04-03-2012 - 20:38
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$|2(a_{n+1}-2012)-(a_n-2012)|<\epsilon$
Implies
$|a_{n+1}-2012|<\dfrac{\epsilon}{2}+\dfrac{1}{2}|a_n-2012| <\dots<\epsilon(\dfrac{1}{2}+\dfrac{1}{4}+\dots+\dfrac{1}{2^{n-n_0}})=\epsilon(1-(\dfrac{1}{2} )^{n-n_0})<\epsilon$
We have $\lim a_n=2012$
#302006 Đề thi Olympic toán sinh viên cấp trường của Đại học kinh tế quốc dân năm 2012
 Đã gửi bởi
analysis90
on 03-03-2012 - 13:16
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 03-03-2012 - 13:16
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$\int_0^xg(y)dy=(\int_0^yf(t)dt)^{2012}\geq 0$.
Assign $h(x)=\int_0^xg(t)dt$. So, we have $h'(x)=g(x)$.
Because $g(x)$ be a nonincreasing, so $g(x)\leq g(0),\forall x\in[0,+\infty)$. Therefore
$h'(x)\leq 0,\forall x\in[0,+\infty)$ or $h(x)\leq h(0)=0,\forall x\in[0,+\infty)$
Implies
$h(x)=0,\forall x\in[0,+\infty)$.
Similarly for $x\in(-\infty,0]$. We have $h(x)=0$ or $g(x)=0,\forall x\in \mathbb{R}$.
When $\int_0^xf(t)dt=0,\forall x\in\mathbb{R}$. Easily, we prove that $f(x)=0$
#300784 [Thắc mắc] Về kỳ thi Olympic Toán Sinh Viên
 Đã gửi bởi
analysis90
on 24-02-2012 - 19:00
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 24-02-2012 - 19:00
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
#299901 Đề thi Olympic toán học sinh viên 2012 Đại Học BK Hà Nội
 Đã gửi bởi
analysis90
on 18-02-2012 - 22:13
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 18-02-2012 - 22:13
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Therefore $|f(t)|\leq \int_0^1|f(x)|dx+t\int_0^t|f'(x)|dx+(1-t)\int_t^1|f'(x)|dx$.
Final, we choose $t=\dfrac{1}{2} $.
#299894 Đề thi Olympic toán học sinh viên 2012 Đại Học BK Hà Nội
 Đã gửi bởi
analysis90
on 18-02-2012 - 21:37
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 18-02-2012 - 21:37
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
So, $0\leq 6^{n+1}|2-x_{n+1}|<\dfrac{6}{7}|2-x_n|<...<(\dfrac{6}{7} )^n|2-\sqrt[3]{6}|\rightarrow 0 $
#299744 Đề thi Olympic toán sinh viên cấp trường của Đại học kinh tế quốc dân năm 2012
 Đã gửi bởi
analysis90
on 17-02-2012 - 15:44
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 17-02-2012 - 15:44
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
We have $\int_0^1(f(x)-6x+2)^2dx\geq 0$, but $\int_0^1(f(x)-6x+2)^2dx=\int_0^1(f(x))^2dx-4$
#299639 Ôn thi Olympic Toán học sinh viên 2015 [Giải tích]
 Đã gửi bởi
analysis90
on 16-02-2012 - 16:06
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 16-02-2012 - 16:06
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$f(x)\leq \int_0^x t^{2012}f(t)dt , \forall x \in [0,1]$.
#299546 Ôn thi Olympic Toán học sinh viên 2015 [Giải tích]
 Đã gửi bởi
analysis90
on 15-02-2012 - 21:53
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
analysis90
on 15-02-2012 - 21:53
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
$\int_0^{1}f(x)dx=(xF(x))|_0^{1}=F(1)$
$2\int_{\dfrac{1}{4}}^{\dfrac{3}{4}}f(x)dx=\dfrac{3}{2}F(\dfrac{3}{4})-\dfrac{1}{2}F(\dfrac{1}{4}) $.
Implies
$3F(\dfrac{3}{4} )-F(\dfrac{1}{4} )=2F(1)$
$\Leftrightarrow F(\dfrac{3}{4})-F(\dfrac{1}{4})=2(F(1)-F(\dfrac{3}{4}))$
So, there exist $\theta_{1}\in (\dfrac{1}{4},\dfrac{3}{4})$ and $\theta_{2}\in (\dfrac{3}{4},1)$ such that
$F'(\theta_1)\dfrac{1}{2}=2.F'(\theta_2)\dfrac{1}{4}$
$\Rightarrow F'(\theta_1)= F'(\theta_2)$
we have $\theta\in (\theta_1,\theta_2)$ such that $F''(\theta)=0$ or
$\dfrac{2}{\theta^3} \int_0^{\theta}f(t)dt-\dfrac{2}{\theta^2}f(\theta)+\dfrac{1}{\theta}f'(\theta)=0 $
Next, assignment $H(x)=2\int_0^{x}f(t)dt-2xf(x)+x^2f'(x)$
$\Rightarrow H(0)=0, H(\theta)=0$
$\exists x_0\in (0,\theta):H'(x_0)=0$
But $H'(x)=x^2f''(x)$
Final $f''(x_0)=0$
#259107 Dùng hàm liên tục, chứng minh nghiệm phương trình
 Đã gửi bởi
analysis90
on 26-04-2011 - 14:27
trong
Hàm số - Đạo hàm
Đã gửi bởi
analysis90
on 26-04-2011 - 14:27
trong
Hàm số - Đạo hàm
2. Tương tự ta cũng xét $f(x)=(9-5m)x^5+(m^2-1)x^4-1$. Nếu $m=\dfrac{9}{5}$ thì pt trở thành $x^4=\dfrac{25}{56}$
nếu $m\neq \dfrac{9}{5}$ thì không mất tính tổng quát ta có thể xét th $m<\dfrac{9}{5}$ khi đó với $x$ đủ lớn $(x\rightarrow + \infty )$ thì $f(x)\rightarrow +\infty$, ngược lại khi $x$ đủ bé $(x\rightarrow -\infty)$ thì $f(x)\rightarrow -\infty$. Vì $f(x)$ liên tục nên tồn tại $x_{0}:f(x_{0})=0$. Th $m>\dfrac{9}{5}$ thì tương tự.
3. Tương tự (sử dụng định lý Rolle).
4. Tham khảo bài giải Olympic giải tích 2011.
#240555 1 bài toán không hề dễ
 Đã gửi bởi
analysis90
on 11-09-2010 - 21:05
trong
Bất đẳng thức và cực trị
Đã gửi bởi
analysis90
on 11-09-2010 - 21:05
trong
Bất đẳng thức và cực trị
trừ hai vế pt ta có pt $(x-y)(x^2+y^2+xy-1)=0\Leftrightarrow$ $x=y$ hoặc $x^2+y^2+xy-1=0$
với x=y thì $x^3+x-2=0 \Leftrightarrow (x-1)(x^2+x+2)=0$
với $X^2+y^2+xy-1=0$ thì bó tay
#239119 Nice but maybe not very hard
 Đã gửi bởi
analysis90
on 02-09-2010 - 15:30
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
analysis90
on 02-09-2010 - 15:30
trong
Bất đẳng thức - Cực trị
đặt $M=VT$
do $abcd=1$ nên tồn tại các số thực dương $x,y,z,t$ sao cho $a=\dfrac{\displaystyle x}{\displaystyle y},b=\dfrac{\displaystyle y}{\displaystyle x},c=\dfrac{\displaystyle z}{\displaystyle t},d=\dfrac{\displaystyle t}{\displaystyle z}$.
khi đó
$M=\dfrac{\displaystyle y^3}{\displaystyle (x+y)(x^2+y^2)}+\dfrac{\displaystyle z^3}{\displaystyle (y+z)(y^2+z^2)}+\dfrac{\displaystyle t^3}{\displaystyle (z+t)(z^2+t^2)}+\dfrac{\displaystyle x^3}{\displaystyle (t+x)(t^2+x^2)}$
nhưng ta có $(x+y)(x^2+y^2)\leq 2(x^3+y^3)\hspace*{1 cm} \forall x,y>0$
$ \Rightarrow \dfrac{\displaystyle y^3}{\displaystyle (x+y)(x^2+y^2)}\geq\dfrac{\displaystyle y^3}{\displaystyle 2(x^3+y^3)}$
khi đó $M\geq\dfrac{\displaystyle 1}{\displaystyle 2}[\dfrac{\displaystyle y^3}{\displaystyle x^3+y^3}+\dfrac{\displaystyle z^3}{\displaystyle y^3+z^3}+\dfrac{\displaystyle t^3}{\displaystyle z^3+t^3}+\dfrac{\displaystyle x^3}{\displaystyle t^3+x^3}]$
đến đây chỉ việc áp dụng bất đẳng thức Nesbitt cho 4 biến $x^3,y^3,z^3,t^3$ ta co ngay $M\geq1$
#239113 Một số bài bdt khó nhờ các bạn giai quyết giúp mình với
 Đã gửi bởi
analysis90
on 02-09-2010 - 14:24
trong
Bất đẳng thức và cực trị
Đã gửi bởi
analysis90
on 02-09-2010 - 14:24
trong
Bất đẳng thức và cực trị
#239112 Một số bài bdt khó nhờ các bạn giai quyết giúp mình với
 Đã gửi bởi
analysis90
on 02-09-2010 - 14:18
trong
Bất đẳng thức và cực trị
Đã gửi bởi
analysis90
on 02-09-2010 - 14:18
trong
Bất đẳng thức và cực trị
$P+12=3(\dfrac{\displaystyle a}{\displaystyle b+c}+1)+4(\dfrac{\displaystyle b}{\displaystyle c+a}+1)+5(\dfrac{\displaystyle c}{\displaystyle a+b}+1)$
$\Leftrightarrow P+12=(a+b+c)(\dfrac{\displaystyle 3}{\displaystyle b+c}+\dfrac{\displaystyle 4}{\displaystyle a+c}+\dfrac{\displaystyle 5}{\displaystyle b+a})$
$\Leftrightarrow P+12=\dfrac{\displaystyle 1}{\displaystyle 2}[(b+c)+(a+c)+(b+a)](\dfrac{\displaystyle 3}{\displaystyle b+c}+\dfrac{\displaystyle 4}{\displaystyle a+c}+\dfrac{\displaystyle 5}{\displaystyle b+a})$
$\geq \dfrac{\displaystyle (\sqrt{3}+2+\sqrt{5})^2}{\displaystyle 2}$
#238931 Khó không hiểu nổi
 Đã gửi bởi
analysis90
on 01-09-2010 - 12:23
trong
Các bài toán Đại số khác
Đã gửi bởi
analysis90
on 01-09-2010 - 12:23
trong
Các bài toán Đại số khác
#238408 cac anh olympic cuu em
 Đã gửi bởi
analysis90
on 28-08-2010 - 14:14
trong
Phương trình - Hệ phương trình - Bất phương trình
Đã gửi bởi
analysis90
on 28-08-2010 - 14:14
trong
Phương trình - Hệ phương trình - Bất phương trình
#238188 Giai pt
 Đã gửi bởi
analysis90
on 25-08-2010 - 22:18
trong
Các bài toán Đại số khác
Đã gửi bởi
analysis90
on 25-08-2010 - 22:18
trong
Các bài toán Đại số khác
#238176 giup em anh chi oi
 Đã gửi bởi
analysis90
on 25-08-2010 - 21:11
trong
Các bài toán Đại số khác
Đã gửi bởi
analysis90
on 25-08-2010 - 21:11
trong
Các bài toán Đại số khác
#237966 Giải hoài không ra
 Đã gửi bởi
analysis90
on 23-08-2010 - 11:02
trong
Các bài toán Đại số khác
Đã gửi bởi
analysis90
on 23-08-2010 - 11:02
trong
Các bài toán Đại số khác
$ \Rightarrow f'(x)=-\displaystyle\dfrac{1}{ 3}ln3.3^{\displaystyle\dfrac{ x}{ 3}}-1<0$
vay nếu pt co nghiệm thì sẽ có nghiệm duy nhất. ta thay x=3
#237964 giup minh voi cac ban oi
 Đã gửi bởi
analysis90
on 23-08-2010 - 10:44
trong
Đại số
Đã gửi bởi
analysis90
on 23-08-2010 - 10:44
trong
Đại số
#237927 Các bạn ơi, giúp tớ bài hình 7 nhé
 Đã gửi bởi
analysis90
on 22-08-2010 - 22:18
trong
Hình học
Đã gửi bởi
analysis90
on 22-08-2010 - 22:18
trong
Hình học
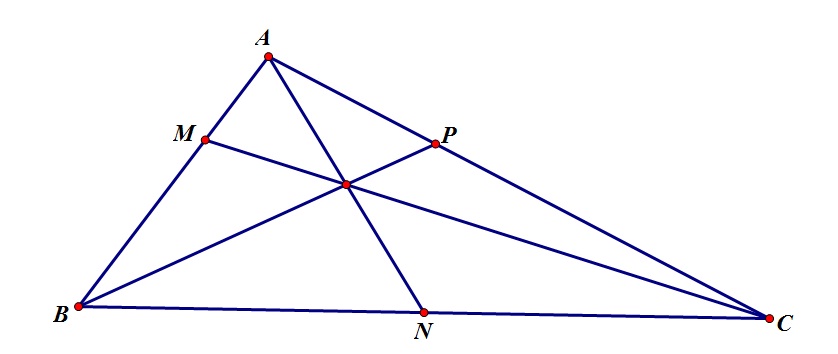
khi đó dưa vào file hình 2 ta có ngay điều cần chứng minh.( chúng đồng qui tại O là trung điểm của MN)
- Diễn đàn Toán học
- → analysis90 nội dung