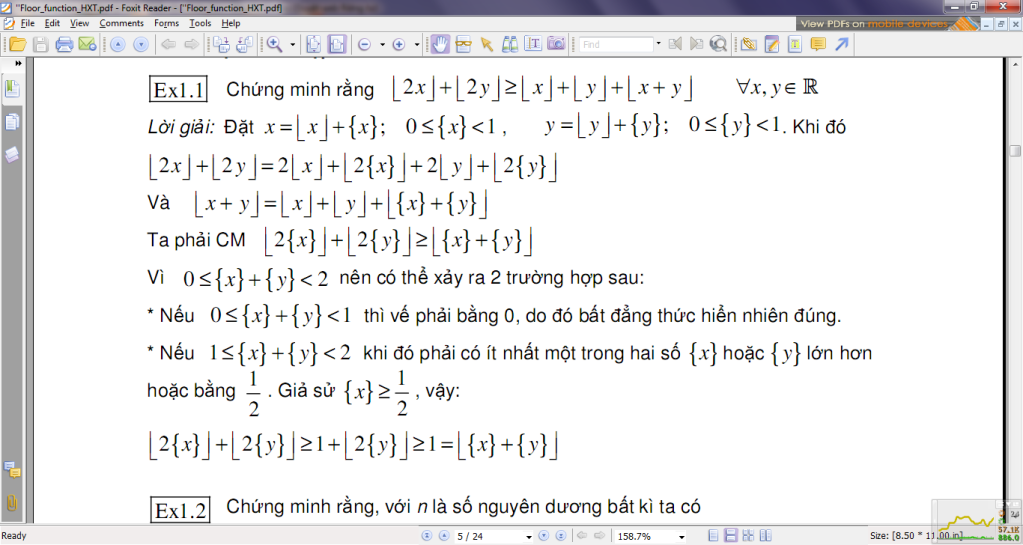
Bài toán [ Vasile Cirtoaje ]
Cho các số thực $a,b,c$ không âm và không có 2 số nào đồng thời bằng 0. Chứng minh rằng :
$$\dfrac{(-a+b+c)^2}{b^2+c^2}+\dfrac{(a-b+c)^2}{c^2+a^2}+\dfrac{(a+b-c)^2}{a^2+b^2}\ge \dfrac{3}{2}$$

Có:
$$\dfrac{(-a+b+c)^2}{b^2+c^2}-\dfrac{1}{2}=\dfrac{2a^2+b^2+c^2-4ab-4ac+4bc}{2(b^2+c^2)}\ge \dfrac{4bc-2ab-2ac}{2(b^2+c^2)}=\dfrac{2bc-ab-ac}{b^2+c^2}$$
Vậy ta chỉ cần c/m:
$$\sum \dfrac{2bc-ab-ac}{b^2+c^2}\ge 0\ \ (*)$$
Thật vậy:
$$(*)\Leftrightarrow \sum \left[ \dfrac{b}{b^2+c^2}(c-a)-\dfrac{c}{b^2+c^2}(a-b) \right]\ge 0\\ \Leftrightarrow \sum \left[ (c-a)\left(\dfrac{b}{b^2+c^2}-\dfrac{b}{a^2+b^2} \right)\right]\ge 0\\ \Leftrightarrow \sum \left[ \dfrac{b(a+c)}{(a^2+b^2)(b^2+c^2)}(c-a)^2\right]\ge 0$$
Hiển nhiên đúng do $a,b,c$ không âm.
Dấu bằng xảy ra khi và chỉ khi $a=b=c\ \square$
---
@White: Mình thử với $(1;1;0)$ không xảy đẳng thức đâu

Cách 2:

Xét hàm số $f\left( t \right) = t - \frac{2}{t},\,\,\,t \ne 0$

Cách này có vẻ gọn hơn ạ . Có $f'(t)=1+\frac{2}{t^2}>0 \forall t\in R\Rightarrow f(x)$ đồng biến trên R\{0} nên pt bên trên sẽ tương đương với $x=y$ đỡ phải xét $xy=-2$ vì đằng nào cũng vô nghiệm
P/s: Ơ tưởng phải vn chứ

Giải như sau:
Chuẩn hoá $abc=1$
Qua PP U.C.T ta có thể tìm được BDT phụ sau:
$\frac{a^3+2abc}{a^3+(b+c)^3}\geq \frac{a^2}{a^2+b^2+c^2}$
That vậy điều này tương đương với:
$a^3b^2+a^3c^2+2abc(a^2+b^2+c^2)\geq 3a^2bc(b+c)+b^3a^2+c^3a^2$
$\Leftrightarrow \frac{a^2b}{c}+\frac{a^2c}{b}+2(a^2+b^2+c^2)\geq \frac{b^2a}{c}+\frac{c^2a}{b}+3ab+3ac\Leftrightarrow$
$(a-b)^2(\frac{c}{b}+1)+(a-c)^2(\frac{b}{c}+1)+(b-c)^2(1-\frac{a}{c}-\frac{a}{b})\geq 0$
TH1: $a\geq b\geq c\Rightarrow S_b,S_c>0,a^2Sb+b^2S_a=\frac{a^2b}{c}+a^2+b^2-\frac{ab^2}{c}-ab\geq 0$ ( Dễ thấy)
TH2:$a\leq b\leq c$, ta có:$S_b\geq 0,S_c+S_b\geq 0,S_b+S_a=2-\frac{a}{c}-\frac{a}{b}+\frac{b}{c}\geq 0$ do $\frac{a}{c}+\frac{a}{b}\leq 1+1=2$
Do đó BDT trên đúng
Thiết lập các BDT tương tự rồi cộng vào ta có đpcm
Đẳng thức xảy ra khi và chỉ khi $a=b=c$ hoặc $a=b,c=0$ và các hoán vị.

BĐT trên chỉ đối xứng với $b$ và $c$ thôi nên liệu xét 2 TH trên đã đủ? Mình hiểu ý bạn là "KMTTQ", giả sử $b$ nằm giữa $a,c$ nên xét 2 TH trên. Nhưng trên thực tế là đã mất tính tổng quát .

Bài toán 2.[Trần Nam Dũng]
Ch0 $x,y,z\geq 0$ và đôi một khác nhau.Chứng minh rằng:
$$(xy+yz+zx)\left[\frac{1}{(x-y)^2}+\frac{1}{(y-z)^2}+\frac{1}{(z-x)^2}\right]\geq 4$$

OTHER SOLUTION:

KMTTQ, giả sử $z=min{x;y;z}$, suy ra:
$xy+yz+zx\ge xy$ và $\dfrac{1}{(x-y)^2}+\dfrac{1}{(y-z)^2}+\dfrac{1}{(z-x)^2}\ge \dfrac{1}{(x-y)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}$
Vậy ta chỉ cần c/m:
$$\dfrac{1}{(x-y)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge \dfrac{4}{xy}\\ \Leftrightarrow \dfrac{(x^2+y^2-3xy)^2}{x^2y^2(x-y)^2}\ge 0$$
Luôn đúng. Dấu bằng vẫn thế $\square$
----
Vì ta đã dự được điểm rơi từ trước nên dùng cách này khá gọn .

Bài toán 2.[Trần Nam Dũng]
Ch0 $x,y,z\geq 0$ và đôi một khác nhau.Chứng minh rằng:
$$(xy+yz+zx)\left[\frac{1}{(x-y)^2}+\frac{1}{(y-z)^2}+\frac{1}{(z-x)^2}\right]\geq 4\ (*)$$

KMTTQ, giả sử $z=min{x;y;z}$. Ta giảm $(x,y,z)$ cùng đi một lượng $z$ (tức là thay $(x;y;z)$ bởi $(x-z;y-z;0)$) thì rõ ràng các hiệu $x-y;y-z;z-x$ không đổi , và $(x-z)(y-z)<xy+yz+zx$. Vậy $VT(*)$ thì giảm đi còn $VP(*)$ thì không đổi. Do đó ta chỉ cần c/m BĐT $(*)$ trong trường hợp $x,y>z=0$.

Thật vậy, với $x,y>z=0$ thì:
$$(*) \Leftrightarrow xy \left [ \dfrac{1}{(x-y)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2} \right ]\ge 4\\ \Leftrightarrow \dfrac{xy}{(x-y)^2}+\dfrac{x^2+y^2}{xy}\ge 4\\ \Leftrightarrow \dfrac{xy}{(x-y)^2}+\dfrac{(x-y)^2}{xy}\ge 2$$

Hiển nhiên đúng theo $AM-GM$. BĐT $(*)$ được c/m. Dấu bằng xảy ra khi:$\left\{\begin{matrix}(x-y)^2=xy\\ z=0\end{matrix}\right.$
$\Leftrightarrow (x;y;z)=\left (k;\dfrac{k(3+\sqrt{5})}{2};0\right );\left (k;\dfrac{k(3-\sqrt{5})}{2};0\right )\ (k> 0)$. và các hoán vị $\square$

Với $a=b=c=\frac{1}{2}$, BĐT sai.
Theo em đề đúng là:
Cho $a,b,c>0$. CMR:
$(1+a)(1+b)(1+c) \geq (1+\sqrt[3]{abc})^3$
Đây chính là hệ quả BĐT Holder

Cho $a,b,c>0$. CMR
$(a^{2}+ab+bc)(b^{2}+bc+ca)(c^{2}+ca+ab)\ge (ab+bc+ca)^{3}$

KMTTQ, giả sử $a$ nằm giữa $b$ và $c$. Áp dụng BĐT $Holder$ ta có:
$$(a^2+ab+bc)(ac+b^2+bc)(c^2+a^2+bc)\ge (ac+ab+bc)^3$$

Vậy ta cần chứng minh:
$$c^2+ca+ab\ge c^2+a^2+bc\\ \Leftrightarrow (a-b)(a-c)\le 0$$

Đúng theo điều giả sử. Vậy BĐT đã cho được c/m, dấu bằng xảy ra khi và chỉ khi $a=b=c$ $\square$

Cho các số thực $a, b, c$ thỏa mãn $(a+c)(a+b+c) \le 0$. Chứng minh rằng: $$(b-c)^2 \ge 4a(a+b+c)$$

Xét đa thức $f(x)=ax^2+(b-c)x+a+b+c$.
Giả thiết đã cho trở thành: $2.f(1)f(0)\le 0\Rightarrow$ pt $f(x)=0$ có nghiệm
$$\Rightarrow \Delta =(b-c)^2-4a(a+b+c)\ge 0\Rightarrow Q.E.D$$

@Dark templar:Khúc $2f(1)f(0) \le 0$ không đúng.$f(1)=2(a+b)$

1/ Tích n số tự nhiên liên tiếp là số chính phương khi 1 trong các số đó bằng 0
-Áp dụng có $x={2011;2012;2013}$
2/ $(x+y)^2=(x-1)(y+1)\leq \frac{(x-1+y+1)^2}{4}=\frac{(x+y)^2}{4}\Rightarrow \frac{3}{4}(x+y)^2\leq 0$
Việc còn lại là ...

4.$\sqrt{\frac{1-x}{x}}=\frac{2x+x^{2}}{1+x^{2}}$

Giải pt đó, có nhõn 1 ẩn . Mod chuyển sang topic pt-hệ pt nhé:
ĐK: ...
$\sqrt{\frac{1-x}{x}}=\frac{2x+x^2}{1+x^2} $. Tự tìm đk nha.$\sqrt{\frac{1-x}{x}}-1=\frac{2x+x^2}{1+x^2}-1$
$\Leftrightarrow \frac{\sqrt{1-x}-\sqrt{x}}{\sqrt{x}}=\frac{2x-1}{x^2+1}$
$\Leftrightarrow \frac{1-2x}{\sqrt{x}.(\sqrt{1-x}+\sqrt{x})}=\frac{2x-1}{x^2+1}$
$\Leftrightarrow (2x-1)(\frac{1}{x^2+1}+\frac{1}{\sqrt{x}.(\sqrt{1-x}+\sqrt{x})})=0$
$\Leftrightarrow x=\frac{1}{2}$

Trong chuyên đề của thầy Thanh có bài này:

Mà nên move topic sang box Số thì đúng hơn

http://diendantoanho...showtopic=68132

Năm nay KHTN không có nhất.
Thầy Lương kiểu j cũng tổng xỉ vả rồi

Bài toán 8: Cm Nesbit 4 biến khi vừa cm được Nesbit 3 biến (Nesbit được coi là lớp 9 không nhỉ ?)
Cho 4 số thực dương $a,b,c,d$, CMR:
$\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq 2$

Lời giải sai lầm

-Áp dụng BĐT Nesbit 3 biến, ta có:
$\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}\geq \frac{3}{2}$
$\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq \frac{3}{2}$
$\frac{c}{d+a}+\frac{d}{a+b}+\frac{a}{b+c}\geq \frac{3}{2}$
$\frac{d}{a+b}+\frac{a}{b+c}+\frac{b}{c+d}\geq \frac{3}{2}$
Cộng vế với vế ta có:
$3(\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b})\geq 6$
$\Rightarrow \frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\geq 2<Q.E.D>$
Dấu bằng xảy ra khi $a=b=c=d$

Lời giải khá đẹp . Nhưng ta để ý thấy với $a=c;b=d$ thì đẳng thức vẫn xảy ra! Lỗi sai ở đâu

Đây là 4 biến mà

Mặt khác, ta có $x^2\vdots x$ $\Rightarrow 1\vdots x\Rightarrow x=\pm 1$.

Không thể có khẳng định như trên vì gt không cho $x\in Z$ mà
Bài giải đúng thì phải theo phương pháp quy nạp toán học

Đề thi trận 1
Giải hệ phương trình trên tập hợp số thực :
$$\begin{cases}
& \text \sqrt[8]{2.\sqrt[5]{7} - \sqrt[10]{y}} + (17 - \sqrt{37}).z^2 = 544 - 32.\sqrt{37} \(1) \\
& \text x.(9.\sqrt{1 + x^2} + 13.\sqrt{1 - x^2}) + 4\sqrt{y} = 912 \(2)\\
& \text \sqrt{(10.\sqrt{5} + 20).x.(1 - x)} + z.\sqrt[6]{8} = 10 \(3)
\end{cases}$$

SOLUTION:
$TXĐ: \left\{\begin{matrix}2.\sqrt[5]{7} - \sqrt[10]{y}\ge 0\\1-x^2\ge 0\\ y\ge 0\\ x(1-x)\ge 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}0\le y\le 50176\\ 0\le x\le 1\end{matrix}\right.$
-Từ TXĐ ta thấy:
$$4\sqrt{y}\le 4\sqrt{50176}=896\ (*)$$
-Giờ ta c/m:
$$A=x.(9.\sqrt{1 + x^2} + 13.\sqrt{1 - x^2})\le 16\ (**)$$
(Bài này rất quen nhưng tự dưng quên mất cách c/m tự nhiên nên đành làm cách dài >"<)
Thật vậy, áp dụng BĐT $AM-GM$ cho 2 số không âm ta có:
$$9\sqrt{1 + x^2} + 13\sqrt{1 - x^2}=3\sqrt{5}.\sqrt{\dfrac{9}{5}(1+x^2)}+13\sqrt{5}.\sqrt{\dfrac{9}{5}(1-x^2)}\\ \le \dfrac{3+\sqrt{5}}{2}(x^2+\dfrac{14}{5})+\dfrac{13+\sqrt{5}}{2}(-x^2+\dfrac{6}{5})\\ =-5\sqrt{5}x^2+12\sqrt{5}\\ \Rightarrow A\le -5\sqrt{5}x^3+12\sqrt{5}x$$
Nhầm dấu đáng tiếc, phải là ${\color{Red} 3.\sqrt{5}}$
-Xét hàm số $f(x)=-5\sqrt{5}x^3+12\sqrt{5}x$ với $0\le x\le 1$
Có: $f'(x)=-15\sqrt{5}{x^2}+12\sqrt{5}=0 \Leftrightarrow x=\dfrac{2\sqrt{5}}{5}\ \text{Thỏa mãn}$
Lập bảng biến thiên ta thấy : $max_{[0 ;1]} f(x)=16$ khi $x=\dfrac{2\sqrt{5}}{5}$
Không nên làm tắt như vậy
Suy ra : $A=x.(9.\sqrt{1 + x^2} + 13.\sqrt{1 - x^2})\le f(x)\le 16$. BĐT $(**)$ được c/m.
Từ $(*)$ và $(**)$ suy ra :
$$VT(2)\le 896+16=912=VP(2)$$
Theo gt thì BĐT trên xảy ra ở đẳng thức nên suy ra : $x=\dfrac{2\sqrt{5}}{5} ;y=50176$

-Thay $ y=50176$ vào $(1)$ ta được:
$$(17 - \sqrt{37}).z^2 = 32(17-\sqrt{37})\\ \Leftrightarrow z^2=32\Leftrightarrow z=4\sqrt{3} \vee z=-4\sqrt{3}$$
Tuy nhiên thử lại thì chỉ có $ z=4\sqrt{3}$ thỏa mãn $(3)$.

K/L : Hệ đã cho có nghiệm duy nhất $x=\dfrac{2\sqrt{5}}{5} ;y=50176 ;z=4\sqrt{3}\ \square$

Điểm bài: 9

S=48−(23−20)+3×9+0+0=72

Cho $p$ là số nguyên tố, $p>3$ và $n=\frac{2^{2p}-1}{3}$. CMR: $(2^{n+1}-4)\vdots n$.
Toán thủ ra đề
rubik97

Dễ thấy $n\ge \dfrac{2^{2.5}-1}{3}=341$. Với điều kiện này thì:

-Từ giả thiết ta có:
$$3n=2^{2p}-1\\ \Leftrightarrow 3(n-1)=2^{2p}-4=4(2^{p-1}-1)(2^{p-1}+1)\\ =2(2^{p-1}-1)(2^p+2)$$

Lại có:

+) $VP$ chẵn $\Rightarrow 3(n-1)\vdots 2\Rightarrow n-1\vdots 2$ do $(3;2)=1$
+) $2^{p-1}-1\vdots p$ (định lí Fermat nhỏ) và $3\not\vdots p\Rightarrow n-1\vdots p$

-Từ các điều trên suy ra: $n-1\vdots 2p$ do $(2;p)=1$

Vậy nên: $3n=2^{2p}-1\Leftrightarrow 2^{2p}=3n+1\equiv 1\ (mod\ n) \Rightarrow 2^{n-1} \equiv 1\ (mod\ n)\Leftrightarrow 2^{n-1}-1\vdots n$

Suy ra: $2^{n+1}-4=4(2^{n-1}-1)\vdots n\ \square$

Các mở rộng của em thực chất chỉ là hệ quả của MR 1.
D-B=4.4h
E=9
F=1*10=10
S=84.6

*Nhận xét: Chìa khóa của bài toán ban đầu là c/m $2^{n-1}-1\vdots n$.

MR 1: Chứng minh nếu $ n=\dfrac{a^{2p}-1}{a^2-1}$,trong đó a nguyên $,a>1,p$ là số nguyên tố lẻ, $a(a^2-1) \not\vdots p$ thì $n$ là số giả nguyên tố cơ sở $a$.

C/m:

- Trước hết ta có : $n=\dfrac{a^p-1}{a-1}.\dfrac{a^p+1}{a+1}$ và $\dfrac{a^p-1}{a-1}\in \mathbb{Z};\dfrac{a^p+1}{a+1}\in \mathbb{Z}; |\dfrac{a^p-1}{a-1}| \ge 2 $ nên n là hợp số $(1)$

- Giả thiết tương đương:
$$(a^2-1)(n-1)=a^{2p}-a^2=a(a^{p-1}-1)(a^p+a)$$
Do
$+) a^p+a $chẵn
$+) p|a^{p-1}-1$ (định lí Fermat nhỏ)
$+) a^2-1|a^{p-1} -1$ (do $p-1$ chẵn)
$+) p\not | a(a^2-1) $
Dẫn đến $2p|n-1 $
Do $ a^{2p}=n(a^2 -1)+1 \equiv 1(mod\ n) $
Nên $a^{n-1} \equiv 1 (mod\ n)\ (2)$
-Từ $(1)$ và $(2)$ ta có ĐPCM.

MR 2: Chứng minh nếu $ n=\dfrac{a^{2p}-1}{a^2-1}$,trong đó a nguyên $,a>1,p$ là số nguyên tố lẻ, $a(a^2-1) \not\vdots p$ thì $a^{n+1}-a^2\vdots n$

C/m:

Từ mở rộng 1 ta chứng minh được $a^{n-1} \equiv 1 (mod\ n)\ \Leftrightarrow n\ |\ a^{n-1}-1 \Rightarrow n\ |\ a^{n+1}-a^2$ (do $a^{n-1}-1 | a^{n+1}-a^2$ ) $\square$

MR 3: Chứng minh nếu $ n=\dfrac{a^{2p}-1}{a^2-1}$,trong đó a nguyên $,a>1,p$ là số nguyên tố lẻ, $a(a^2-1) \not\vdots p$ thì $a^{n+k-1}-a^{k} \vdots n$ với $k\in \mathbb{N}$

C/m:

Từ mở rộng 1 ta chứng minh được $a^{n-1} \equiv 1 (mod\ n)\ \Leftrightarrow n\ |\ a^{n-1}-1 \Rightarrow n\ |\ a^{n+k-1}-a^{k}$ (do $a^{n-1}-1 | a^{n+k-1}-a^{k}$ ) $\square$

MR 4: Chứng minh nếu $ n=\dfrac{a^{2p}-1}{a^2-1}$,trong đó a nguyên $,a>1,p$ là số nguyên tố lẻ, $a(a^2-1) \not\vdots p$ thì $k(a^{n-1}-1) \vdots n$ với $k\in \mathbb{N}$

C/m:

Từ mở rộng 1 ta chứng minh được $a^{n-1} \equiv 1 (mod\ n)\ \Leftrightarrow n\ |\ a^{n-1}-1 \Rightarrow n\ |\ k(a^{n-1}-1)$ (do $a^{n-1}-1 | k(a^{n-1}-1)$ ) $\square$

Vì trận này không có toán thủ nào nộp đề hoàn chỉnh nên BTC sẽ ra đề.
Đề bài: Tìm tất cả hàm số $f: \mathbb{R} \to \mathbb{R}$
\[ f(x^2+f(y))=y+(f(x))^2 \ (*)\,\, \forall x,y \in \mathbb{R} \]
Thời gian làm bài tính từ 20h ngày 28/09/12

SOLUTION:

Giả sử tồn tại hàm số $f(x)$ thỏa mãn điều kiện bài toán. Thay $(-x;y)$ vào $(*)$ ta có:
$$f((-x)^2+f(y))=y+(f(-x))^2\\\Leftrightarrow f(x^2+f(y))=y+(f(-x))^2\ (1)$$
-Trừ hai vế của $(*)$ cho $(1)$ có:
$$(f(x))^2-(f(-x))^2=0\Leftrightarrow[f(x)-f(-x)][f(x)+f(-x)] =0\\\Leftrightarrow\left[\begin{matrix}f(x)=f(-x)\\ f(x)=-f(-x)\end{matrix}\right.$$

TH 1: $f(x)$ là hàm chẵn. Thay $(x;-y)$ vào $(*)$ ta có:
$$f(x^2+f(y))=-y+(f(x))^2\Rightarrow y=0$$
Mâu thuẫn. Vậy $f(x)$ không phải hàm chẵn

TH 2: $f(x)$ là hàm lẻ. Thay $ (\ x;-(f(x))^2\ ) $ vào $(*)$ ta có:
$$f(x^2-f[(f(x))^2])=0$$
Đặt $a=x^2-f[(f(x))^2]$ thì $f(a)=0\Rightarrow f(-a)=-f(a)=0$
-Thay $(x;a);(x;-a)$ vào $(*)$ ta có:
$$+)\ f(x^2+f(a))=a+(f(x))^2\Rightarrow f(x^2)=a+(f(x))^2\ \ (2)\\ +)\ f(x^2+f(-a))=-a+(f(x))^2\Rightarrow f(x^2)=-a+(f(x))^2\ \ (3)$$
-Trừ hai vế của $(2)$ cho $(3)$ suy ra:
$$2a=0\\ \Leftrightarrow a=0$$
Vậy $f(0)=0$

-Thay $(0;x)$ vào $(*)\Rightarrow f(f(x))=x$
Suy ra $f$ là hàm đối hợp. Mặt khác $f$ là hàm lẻ $\Rightarrow f(x)=x$
Thử lại thấy hàm số $f(x)=x$ thỏa mãn $(*)$

K/L: $f(x)=x$ là hàm số cần tìm $\square$

Lời giải về cơ bản là sai.
$\forall x:f(-x)^2=f(x)^2$ không đồng nghĩa với $f$ là hàm chẵn hoặc $f$ là hàm lẻ.
Vì có thể tồn tại $x;y\ne 0$ để $f(-x)=f(x);f(-y)=-f(y)$.
S=0

Lời giải về cơ bản là sai.
$\forall x: (f(x)=x) \vee (f(x)=-x)$ nhưng không đồng nghĩ $\forall x:f(x)=x$ hoặc $\forall x:f(x)=-x$
S=0

Là sao ạ? em có ghi $\forall x: (f(x)=x) \vee (f(x)=-x)\Leftrightarrow \forall x:f(x)=x$ hoặc $\forall x:f(x)=-x$ ở đoạn nào đâu ?
---
P/s:

Điều 6. Quy định đề bài:
a. Nội dung:
- Mỗi bộ đề bao gồm 1 câu của THPT. Nội dung các đề phải tuân theo thứ tự sau:

+ Tuần 1: Phương trình, hệ phương trình, bất phương trình
+ Tuần 2: Đa thức hoặc Phương trình hàm
+ Tuần 3: Hình học
+ Tuần 4: Dãy số, giới hạn
+ Tuần 5: Số học
+ Tuần 6: Tổ hợp
+ Tuần 7: Bất đẳng thức
Các tuần sau lại lặp lại theo thứ tự trên

- Đề bài không copy nguyên văn từ đề thi Olympic hoặc HSG cấp Quốc gia trở lên.
b. Hình thức:
- Đề bài được gõ $Latex$ rõ ràng.

IMO 1992, Day 1, Problem 2

Chắc ở đây ai cũng biết IMO là thi cấp gì ... ='=.

Chú Hoàng chắc dùng wolfram chứ đạo hàm cái này cũng mệt!

Người ta đã chứng minh được rằng một dãy số hội tụ chỉ có một giới hạn duy nhất.

Vu vơ khéo chuẩn!
P/s: Sao ít người tham gia MO vậy nhỉ?

*C/m hàm số $f(x)=\sin x$ không có giới hạn khi $x\rightarrow +\infty$:

Giả sử $\lim_{x\rightarrow +\infty} \sin x=L$ thì $L$ sẽ tồn tại duy nhất.
Vậy ta sẽ chỉ ra hai dãy số mà khi $x\rightarrow +\infty$ nó làm cho $\sin x$ tiến đến 2 giới hạn khác nhau
Xét dãy $x_1=\dfrac{\pi}{2} +k2\pi$ và dãy $x_2=-\dfrac{\pi}{2} +k2\pi$ (với $k \in \mathbb{Z} $)
Khi $x_1\rightarrow +\infty$ thì $\lim \sin x_1=\lim (\dfrac{\pi}{2} +k2\pi)=1$
Khi $x_2\rightarrow +\infty$ thì $\lim \sin x_2=\lim (-\dfrac{\pi}{2} +k2\pi)=-1$

Rõ ràng 2 giới hạn này khác nhau, mâu thuẫn vì $L$ tồn tại duy nhất.
Vậy không tồn tại giới hạn của hàm số $f(x)=\sin x$ khi $x\rightarrow +\infty$.

Vậy hàm số đã cho không có giới hạn khi $n\rightarrow +\infty\ \square$

Thế em đã chứng minh $\sqrt{n^2+n} \to +\infty$ khi $n \to +\infty$?
D-B=14h
E=9
F=0
S=65

Đề bài đâu cho $x$ nguyên dương đâu?
Một số bạn trước khi viết kí hiệu tổ hợp chập phải có dòng: "Xét $x$ nguyên dương trong khoảng $[0;n]$ ", vì $C^k_n$ chỉ tồn tại khi $k\in \mathbb{N},x\in \mathbb{N^*}$

Lời giải mang phong cách casio quá ,nhưng có lẽ không có cách khác
Tiếp tục ,Bài 37 : Giải phương trình nguyện nguyên dương :

$a^3+b^3+c^3=abc$

Nếu vậy thì dễ hơn so với bài trên ạ :
$abc=a^3+b^3+c^3\ge 3abc\Rightarrow 1\ge 3\ (False)$ (Do $a,b,c>0\Rightarrow abc>0$)
Vậy pt đã cho vô nghiệm
Bài 38:
$x\ge -\frac{1}{4};y\ge 1$
Biến đổi rút gọn VT ta có:
$$\Leftrightarrow (\sqrt{x+\frac{1}{4}}+\frac{1}{2})^2=y\\ \Leftrightarrow \sqrt{x+\frac{1}{4}}=\sqrt{y}-\frac{1}{2}\\ \Leftrightarrow x+\frac{1}{4}=y-\sqrt{y}+\frac{1}{4}\\ \Leftrightarrow x=y-\sqrt{y}$$
Vì $x,y\in Z\Rightarrow \sqrt{y}\in Z$. Đặt $y=k^2(k\in N^*)\Rightarrow x=k^2+k$
...

Trường hợp $abc=a^3+b^3+c^3 = 3abc$
$\Rightarrow$ abc=1
$\Rightarrow$ a=b=c=1

Sai rồi bạn, ngay từ dòng đầu!
Thử lại với $a=b=c=1$ cũng không thỏa mãn vì $VT=3;VP=1$