162 replies to this topic

[Nguyen Minh Hai]

Vế phải là mũ $3$ mới phải 

Mình nhầm :3 

 

P/s: Long Vá xóa bài giùm anh 

[Ngockhanh99k48]

Bài 35/1: Giả sử $c=min(a,b,c)$.
Bất đẳng thức đã cho tương đương:
$\frac{7(a^2+b^2+c^2-ab-bc-ca)}{(a+b+c)(\sqrt{3(a^2+b^2+c^2)}+a+b+c)} \geq \frac{(a-b)^2(a+b)+(a-c)(b-c)(b+c)}{2(a^3+b^3+c^3)}$.
Do $(a-b)^2(a+b)+(a-c)(b-c)(b+c) \leq (a+b+c)(a^2+b^2+c^2-ab-bc-ca)$ nên ta chỉ cần chứng minh:
$14(a^3+b^3+c^3) \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)}$.
Sử dụng Cauchy-Schwarz ta có:
$14(a^3+b^3+c^3) \geq 14\frac{(a^2+b^2+c^2)^2}{a+b+c} \geq \frac{14}{9}.\frac{(a+b+c)^3\sqrt{3(a^2+b^2+c^2)}}{a+b+c} \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)} \blacksquare$.

Edited by Ngockhanh99k48, 18-06-2016 - 09:44.

[Nguyenngoctu]

 

 

 Bài toán 1. (Võ Quốc Bá Cẩn) Cho $a,b,c\geq 0$. Chứng minh rằng \[\sqrt{\dfrac{a(b+c)}{b^2+c^2}}+\sqrt{\dfrac{b(c+a)}{c^2+a^2}}+\sqrt{\dfrac{c(a+b)}{a^2+b^2}}\geq 2\]

 

 

Bài này dùng côsi đảo dễ dàng nhất. BĐT chặt hơn là: $$\sum {\sqrt {\frac{{a\left( {b + c} \right)}}{{{a^2} + bc}}} } \ge 2 + \frac{{8abc}}{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}$$

Edited by Nguyenngoctu, 18-06-2016 - 14:54.

[cristianoronaldo]

Bài này dùng côsi đảo dễ dàng nhất. BĐT chặt hơn là: $$\sum {\sqrt {\frac{{a\left( {b + c} \right)}}{{{a^2} + bc}}} } \ge 2 + \frac{{4abc}}{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}$$

Áp dụng bất đẳng thức AM-GM ta có:

$\sqrt{\frac{a(b+c)}{a^2+bc}}= \frac{a(b+c)}{\sqrt{(a^2+bc).a(b+c)}}\geq \frac{2a(b+c)}{a^2+bc+a(b+c)}=\frac{2a(b+c)}{(a+b)(a+c)}$

Tương tự và cộng theo vế ta được:

$\sum \sqrt{\frac{a(b+c)}{a^2+bc}}\geq 2.\sum \frac{a(b+c)}{(a+b)(a+c)}= \frac{2[a(b+c)^2+b(a+c)^2+c(a+b)^2]}{(a+b)(b+c)(c+a)}= 2+\frac{4abc}{(a+b)(b+c)(c+a)}$

Dấu ''='' xảy ra khi a=b=c

[Gachdptrai12]

Bài 35/1: Giả sử $c=min(a,b,c)$.
Bất đẳng thức đã cho tương đương:
$\frac{7(a^2+b^2+c^2-ab-bc-ca)}{(a+b+c)(\sqrt{3(a^2+b^2+c^2)}+a+b+c)} \geq \frac{(a-b)^2(a+b)+(a-c)(b-c)(b+c)}{2(a^3+b^3+c^3)}$.
Do $(a-b)^2(a+b)+(a-c)(b-c)(b+c) \leq (a+b+c)(a^2+b^2+c^2-ab-bc-ca)$ nên ta chỉ cần chứng minh:
$14(a^3+b^3+c^3) \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)}$.
Sử dụng Cauchy-Schwarz ta có:
$14(a^3+b^3+c^3) \geq 14\frac{(a^2+b^2+c^2)^2}{a+b+c} \geq \frac{14}{9}.\frac{(a+b+c)^3\sqrt{3(a^2+b^2+c^2)}}{a+b+c} \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)} \blacksquare$.

$(a+b+c)^{3}$ mất đâu rồi bạn :3 

[Gachdptrai12]

Ta có

\[2\left(\frac{a}b{+\frac{b}c{+\frac{c}{a}}}\right)+1-\frac{21(a^{2}+b^{2}+c^{2})}{(a+b+c)^{2}} = \frac{2\displaystyle \sum a(a-b)^2(b-2c)^2}{abc(a+b+c)^2} \geqslant 0.\]

Từ đó suy ra điều phải chứng minh.

hình như cái phân tích thế nào ấy em phân tích nó ra khác và ko lớn hơn 0 anh xem lại dùm em cảm ơn 

[Nguyenhuyen_AG]

hình như cái phân tích thế nào ấy em phân tích nó ra khác và ko lớn hơn 0 anh xem lại dùm em cảm ơn 

 

Anh đã kiểm tra lại và thấy nó đúng

 

 

[Gachdptrai12]

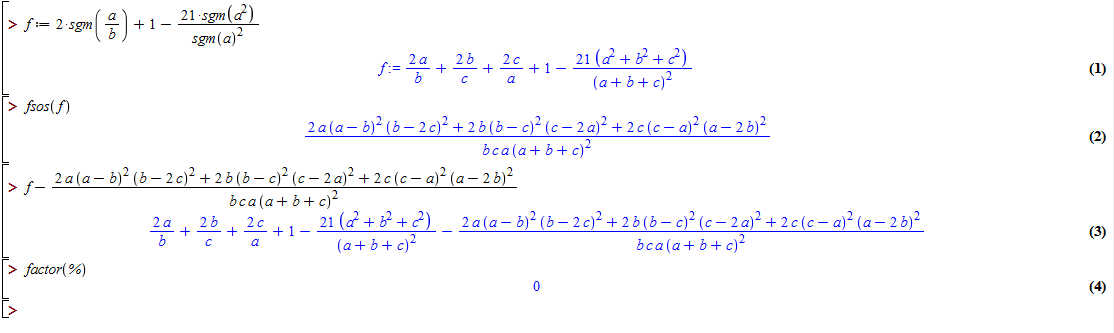
Anh đã kiểm tra lại và thấy nó đúng

 

èo srry em chưa phân tích hết ra   

[fatcat12345]

Cho em hỏi là anh dùng thuật toán như thế nào để phân tích ra các hệ số không âm vậy ạ? Em phân tích ra dạng SOS mà các hệ số có âm có dương khá là khó đánh giá

Edited by fatcat12345, 23-06-2016 - 01:34.

[Nguyenhuyen_AG]

Cho em hỏi là anh dùng thuật toán như thế nào để phân tích ra các hệ số không âm vậy ạ? Em phân tích ra dạng SOS mà các hệ số có âm có dương khá là khó đánh giá

 

Anh dùng hệ số bất định.

[fatcat12345]

Vì topic lâu rồi cũng dậm tại chỗ nên mình xin phép đề xuất bài mới.

Bài toán 36 (Sưu tầm) Cho $a,b,c,x,y,z\geq 0$. Chứng minh

$$x(b+c)+y(c+a)+z(a+b)\geq 2\sqrt{(xy+yz+zx)(ab+bc+ca)}.$$

Edited by fatcat12345, 23-06-2016 - 16:44.

[Ngockhanh99k48]

Áp dụng Cauchy-Schwarz ta có
$x(b+c)+y(c+a)+z(a+b) = (a+b+c)(x+y+z)-(ax+by+cz) = \sqrt{[(a^2+b^2+c^2)+2(ab+bc+ca)][(x^2+y^2+z^2)+2(xy+yz+zx)]}-(ax+by+cz) \geq 2\sqrt{(ab+bc+ca)(xy+yz+zx)}+\sqrt{(a^2+b^2+c^2)(x^2+y^2+z^2)}-(ax+by+cz) \geq 2\sqrt{(ab+bc+ca)(xy+yz+zx)}$.

[quykhtn-qa1]

Bài 35 có thể chứng minh dựa vào đẳng thức sau, chú ý là có thể tìm ra và tính toán bằng tay chứ không phải dùng máy tính:
http://artofproblems...231645p3507509 

 

Bài toán 37. (AoPS) . Cho các số thực không âm $a,b,c$. Chứng minh rằng

$$\sqrt{a^2+bc+b^2}+\sqrt{b^2+ca+c^2}+\sqrt{c^2+ab+a^2} \geq \sqrt{4(a^2+b^2+c^2)+5(ab+bc+ca)}.$$

[Nguyenhuyen_AG]

Bài 35 có thể chứng minh dựa vào đẳng thức sau, chú ý là có thể tìm ra và tính toán bằng tay chứ không phải dùng máy tính:
http://artofproblems...231645p3507509 

 

An interesting proof for you, manilo! 

\[{ 6\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)+3-7(a^2+b^2+c^2)=\dfrac{2}{3} \cdot \left[\dfrac{(2b-c)^2(a-b)^2}{bc}+\dfrac{(2c-a)^2(b-c)^2}{ca}+\dfrac{(2a-b)^2(c-a)^2}{ab} \right].}\]

 

 

Đẳng thức này sai.

[quykhtn-qa1]

Đẳng thức này đúng, chú ý $a+b+c=3.$

[Nguyenhuyen_AG]

Đẳng thức này đúng, chú ý $a+b+c=3.$

 

Cho $a=1,\,b=\frac{1}{2},\,c=\frac{3}{2}$ thì $a+b+c=3$

\[6\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)+3-7(a^2+b^2+c^2) = \frac{3}{2},\]

và

\[\dfrac{2}{3} \cdot \left[\dfrac{(2b-c)^2(a-b)^2}{bc}+\dfrac{(2c-a)^2(b-c)^2}{ca}+\dfrac{(2a-b)^2(c-a)^2}{ab} \right] = \frac{31}{12}.\]

 

Bài 35 có thể chứng minh dựa vào đẳng thức sau, chú ý là có thể tìm ra và tính toán bằng tay chứ không phải dùng máy tính:

Tất nhiên là làm hoàn toàn bằng tay, những phân tích kiểu này anh Cẩn cũng đã từng hướng dẫn trong tạp chí Epsilon số 1.

[quykhtn-qa1]

Đẳng thức chuẩn của bài này là: Với $a+b+c=3,$ ta có

 

\[ 6\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)+3-7(a^2+b^2+c^2)\]

\[=\dfrac{2}{3}\cdot \left[\dfrac{(2c-b)^2(a-b)^2}{bc}+\dfrac{(2a-c)^2(b-c)^2}{ca}+\dfrac{(2b-a)^2(c-a)^2}{ab}\right]. \]

 

[fatcat12345]

 

Bài toán 37. (AoPS) . Cho các số thực không âm $a,b,c$. Chứng minh rằng

$$\sqrt{a^2+bc+b^2}+\sqrt{b^2+ca+c^2}+\sqrt{c^2+ab+a^2} \geq \sqrt{4(a^2+b^2+c^2)+5(ab+bc+ca)}.$$

 

Lời giải bài 37.

Giả sử $c=min\left \{ a,b,c \right \}.$

Ta chứng minh

$$\sqrt{a^2+bc+b^2}+\sqrt{c^2+ab+a^2}\geq \sqrt{a^2+ab+b^2}+\sqrt{c^2+bc+a^2}$$

bình phương và thu gọn ta cần chứng minh

$$(a^2+bc+b^2)(c^2+ab+a^2)\geq (a^2+ab+b^2)(c^2+bc+a^2)$$

$$\Leftrightarrow b(b+c)(b-c)(a-c)\geq 0$$

Ta cũng chứng minh

$$\sqrt{b^2+ca+c^2}+\sqrt{a^2+bc+c^2}\geq \sqrt{b^2+bc+c^2}+\sqrt{c^2+ca+a^2}$$

bình phương và thu gọn ta cần chứng minh

$$(b^2+ca+c^2)(a^2+bc+c^2)\geq (b^2+bc+c^2)(c^2+ca+a^2)$$

$$\Leftrightarrow c(a+b)(a-b)^2\geq 0$$

Từ 2 bất đẳng thức trên ta dễ dàng suy ra

$$\sum_{cyc}\sqrt{a^2+bc+b^2}\geq \sum_{cyc}\sqrt{a^2+ab+b^2}$$

nên ta chỉ cần chứng minh

$$\sum_{cyc}\sqrt{a^2+ab+b^2}\geq \sqrt{4(a^2+b^2+c^2)+5(ab+bc+ca)}$$

bình phương và thu gọn ta cần chứng minh

$$\sum_{cyc}\sqrt{(a^2+ab+b^2)(b^2+bc+c^2)}\geq (a+b+c)^2$$

ta lại có $(a^2+ab+b^2)(b^2+bc+c^2)-\left [ b^2+\frac{b(c+a)}{2}+ca \right ]^2=\frac{3}{4}b^2(c-a)^2\geq 0$

nên

$$\sum_{cyc}\sqrt{(a^2+ab+b^2)(b^2+bc+c^2)}\geq \sum_{cyc}\left [ b^2+\frac{b(c+a)}{2}+ca \right ]=(a+b+c)^2$$

Xong!

Edited by fatcat12345, 26-06-2016 - 19:59.

[Gachdptrai12]

Lời giải bài 37.

Giả sử $c=min\left \{ a,b,c \right \}.$

Ta chứng minh

$$\sqrt{a^2+bc+b^2}+\sqrt{c^2+ab+a^2}\geq \sqrt{a^2+ab+b^2}+\sqrt{c^2+bc+a^2}$$

bình phương và thu gọn ta cần chứng minh

$$(a^2+bc+b^2)(c^2+ab+a^2)\geq (a^2+ab+b^2)(c^2+bc+a^2)$$

$$\Leftrightarrow b(b+c)(b-c)(a-c)\geq 0$$

Ta cũng chứng minh

$$\sqrt{b^2+ca+c^2}+\sqrt{a^2+bc+c^2}\geq \sqrt{b^2+bc+c^2}+\sqrt{c^2+ca+a^2}$$

bình phương và thu gọn ta cần chứng minh

$$(b^2+ca+c^2)(a^2+bc+c^2)\geq (b^2+bc+c^2)(c^2+ca+a^2)$$

$$\Leftrightarrow c(a+b)(a-b)^2\geq 0$$

Từ 2 bất đẳng thức trên ta dễ dàng suy ra

$$\sum_{cyc}\sqrt{a^2+bc+b^2}\geq \sum_{cyc}\sqrt{a^2+ab+b^2}$$

nên ta chỉ cần chứng minh

$$\sum_{cyc}\sqrt{a^2+ab+b^2}\geq \sqrt{4(a^2+b^2+c^2)+5(ab+bc+ca)}$$

bình phương và thu gọn ta cần chứng minh

$$\sum_{cyc}\sqrt{(a^2+ab+b^2)(b^2+bc+c^2)}\geq (a+b+c)^2$$

ta lại có $(a^2+ab+b^2)(b^2+bc+c^2)-\left [ b^2+\frac{b(c+a)}{2}+ca \right ]^2=\frac{3}{4}b^2(c-a)^2\geq 0$

nên

$$\sum_{cyc}\sqrt{(a^2+ab+b^2)(b^2+bc+c^2)}\geq \sum_{cyc}\left [ b^2+\frac{b(c+a)}{2}+ca \right ]=(a+b+c)^2$$

Xong!

lời giải của bạn là lời giải được lấy từ http://www.artofprob...h507278p2850887

[Nguyenhuyen_AG]

lời giải của bạn là lời giải được lấy từ http://www.artofprob...h507278p2850887

 

Sao em có thể khẳng định như vậy ?