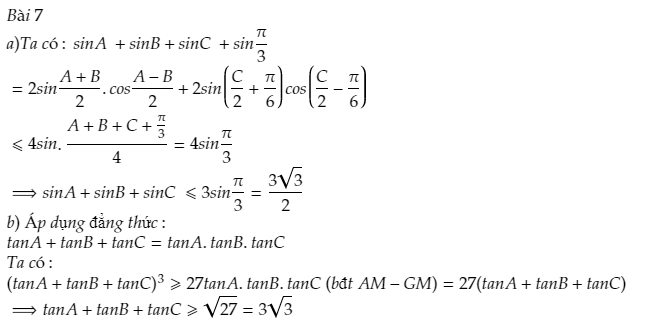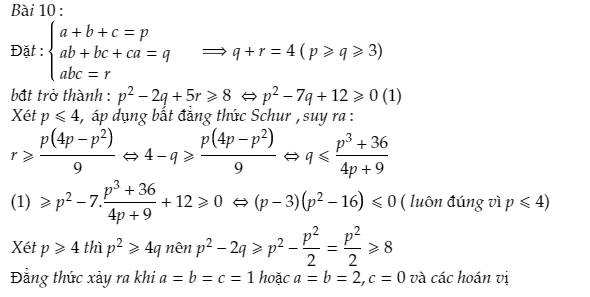$\boxed{7}$ Chứng minh với mọi tam giác ABC, ta có:
$a)$ $sin$ $A$ + $sin$ $B$ + $sin$ $C$ $\leq \frac{3\sqrt{3}}{2}$
$b)$ $tan$ $A$ + $tan$ $B$ + $tan$ $C$ $\geq$ $3\sqrt{3}$ (góc$A,B,C$ nhọn)
Chắc như thế này:
a) Xét hàm số $y=f(x)=sinx,x\in(0;\pi)$. Ta có $f''(x)=-sinx\leq 0,\forall x\in(0;\pi)$ nên f(x) lõm trên $(0;\pi)$.
Do đó theo bất đẳng thức Jensen thì $sinA+sinB+sinC=f(A)+f(B)+f(C)\leq 3f(\frac{A+B+C}{3})=\frac{3\sqrt{3}}{2}$. (đpcm)
b) Xét hàm số $y=f(x)=tanx,x\in(0;\frac{\pi}{2})$. Ta có $f''(x)=\frac{2tanx}{cos^2x}\geq 0,\forall x\in(0;\frac{\pi}{2})$ nên f(x) lồi trên $(0;\frac{\pi}{2})$.
Do đó theo bất đẳng thức Jensen thì $tanA+tanB+tanC=f(A)+f(B)+f(C)\geq 3f(\frac{A+B+C}{3})=3\sqrt{3}$. (đpcm)