Bài 3: Giải hệ phương trình: $\left\{ \begin{array}{l}xy = x + y - z\\yz = 3(y - x + z)\\zx = 2(x - y + z)\end{array} \right.$

Mình là thành viên mới, mình có một cách giải của bài toán này như sau, mong các bạn cho ý kiến :


$\left\{ \begin{array}{l}
xy = x + y - z\,\,\,\,\,\,\,(1) \\
yz = 3(y - x + z)\,\,(2) \\
zx = 2(x - y + z)\,\,(3) \\
\end{array} \right.$

Dễ thấy, nếu xyz=0 thì:
* x=0 => x=y=z=0 hoặc x=0;y=z=6
* y=0 => x=y=z=0 hoặc x=z=4;y=0
* z=0=> x=y=z=0 hoặc x=y=2;z=0
Với xyz khác 0, ta có :

\[
(1) \to z = x + y - xy\,
\]
thế vào (2),(3) ta đc:

\[
\begin{array}{l}
(2) \Leftrightarrow y(x + y - xy) = 3(y - x + x + y - xy) \\
\,\,\,\,\,\,\,\, \Leftrightarrow \,xy + y^2 - xy^2 = 6y - 3xy \\
\,\,\,\,\,\,\,\, \Leftrightarrow \,y(y - xy - 6 + 4x) = 0 \\
\,\,\,\,\,\,\,\, \Leftrightarrow \,y - xy + 4x = 6(vi`\,y \ne 0)\,\,\,\,\,(2') \\
\,\,\,\,\,\,\,\, \\
\end{array}
\]
Bằng việc làm tương tự như trên, ta cũng thế giá trị của z vào (3) và khi đó, ta được phương trình (3'):

\[
x - xy + 3y = 4(3')
\]
Lấy (2') trừ (3') vế theo vế và biến đổi ta được :

\[
y = \frac{{3x - 2}}{2}
\]
Thế giá trị y vừa tìm được vào 1 trong 2 phương trình(2') và (3'), ta được 1 phương trình bậc 2 theo ẩn x hoặc ẩn y, mình làm theo ẩn x và tìm được 2 giá trị của x là \[
\frac{7}{3}
\] và 2 nhưng loại đi giá trị x=2 vì từ đó suy ra y=2 & z=0. Vậy, kết luận, pt có 5 nghiệm (x;y;z)=(0;6;6);(4;0;4);(2;2;0)\[
(0;0;0);(\frac{7}{3};\frac{5}{2}; - 1)
\];
......................
Mình đã đọc cách giải của bạn Phạm Quang Toàn và thấy cách giải đó khá độc đáo, và mình đã cố gắng tìm ra một cách giải khác, đồng ý là không hay bằng cách của bạn Toàn, nhưng mình thường hay cố gắng tìm một những lời giải khác nhau và qua bài toán này, mình xin đưa ra bài toán tổng quát sau

giải hệ phương trình:\[
\left\{ \begin{array}{l}
a_1 xy = b_1 x + \,c_1 y + \,d_1 z) \\
a_2 yz = b_2 y + c_2 x + \,d_2 z) \\
a_3 xz = \,b_3 x + c_3 y + d_3 z) \\
\end{array} \right.
\]

(Với \[ a_i ,b_i ,c_i ,d_i \, \in \,R;\,(i = \overline {1,3} )\] )

............
Có thể nâng lên nhiều nữa nhưng kế tiếp bài toán của bạn Huy là vấn đề trên mình nêu ra.... Mong các bạn cho ý kiến . tks nhiều

Bài 1. Đặt $x^{2}+x+1=a(a>0); x-1=b.$ thì phương trình đã cho sẽ là
$2a^{2} - 7b^{2} = 13ab
\Leftrightarrow 2a^{2} - 14ab + ab-7b^{2}=0
\Leftrightarrow 2a(a-7b) + b(a-7b)=0

\Leftrightarrow (a-7b)(2a+b)=0$

\[
\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{l}
a = 7b \\
a = - 2b \\
\end{array} \right. \\
\Leftrightarrow \left[ \begin{array}{l}
x^2 + x + 1 = x - 1 \\
x^2 + x + 1 = 2 - 2x \\
\end{array} \right. \\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{{ - 3 + \sqrt {13} }}{2} \\
x = \frac{{ - 3 - \sqrt {13} }}{2} \\
\end{array} \right. \\
\end{array}
\]
Vậy pt có 2 nghiệm ......

câu b sử dụng định lý viete

Cho mình hỏi câu bất đẳng thức , câu 3 ý, có điều kiện a,b,c > 0 hay không? hay với mọi số thực ...

Bài 3: Cho abc=2012
Tìm max: $\frac{1}{a^{3}+b^{3}+abc}+\frac{1}{b^{3}+c^{3}+abc}+\frac{1}{c^{3}+a^{3}+abc}

Hình như thiếu điều kiện a,b,c thì phải. Bạn xem lại thử nhaz

uhm`, như vậy thì sử dụng BĐT $a^{3}+b^{3}\geq ab(a+b)$ là ra ngay thôi bạn à

còn bài ptnn : x+y+z+5=xyz. Bài này có khá nhiều cách giải, nhưng theo mình thì nên sử dụng phương pháp cực hạn, sắp xếp thứ tự ý, vì vai trò của x,y,z trong bài này là như nhau.

giải hệ phương trình sau :

$\left\{ \begin{array}{l}
x^2 + y^2 = 1 \\
125y^5 - 125y^3 + 6\sqrt {15} = 0 \\
\end{array} \right.$


Mong các bạn giúp đỡ, cho ý kiến....

có cách nào khác nữa không?
2 cách này tớ nghĩ ra rồi

Các bạn ở Đà Nẵng ah`, cho mình làm quen với. Mà ở Đà Nẵng thi cấp tỉnh rồi ah`??? Mấy bạn làm được hok, bạn Huy ý, làm được tất cả chứ ????

Bài này cũng khá đơn giản mà ...
Vì p là SNT >3 nên $p=3k+1$ hoặc $p=3k+2$ (k là số tự nhiên)
Nếu $p=3k+1$ thì $2p+1=6k+3 \vdots 3$; và $1<3<2p+1$ nên $2p+1$ là hợp số (mâu thuẫn giả thiết)
Do đó, $p= 3k+2 \Rightarrow 4p+1=12k+9 \vdots 3$ mà $1<3<4p+1 \Rightarrow 4p+1$ là hợp số (đpcm)

Mình thấy cách giải của bạn 'Katyusha' khá hay, nhưng mình cũng có một cách giải khác, không dùng Cauchy-Schwartz,....

Áp dụng BĐT AM-GM, ta có:

$\begin{array}{l}
\,\,\,\frac{{a^3 }}{{1 + b}} + \frac{{1 + b}}{4} + \frac{1}{2} \ge 3\sqrt[3]{{\frac{{a^3 }}{{1 + b}}.\frac{{1 + b}}{4}.\frac{1}{2}}} = \frac{3}{2}a \\
\Rightarrow \,\frac{{a^3 }}{{1 + b}} \ge \frac{3}{2}a - \frac{{1 + b}}{4} - \frac{1}{2} = \frac{3}{2}a - \frac{1}{4}b - \frac{3}{4} \\
\end{array}$ (1)
Tương tự, ta cũng có :

$\frac{{b^3 }}{{1 + a}} \ge \frac{3}{2}b - \frac{1}{4}a - \frac{3}{4}$ (2)
Cộng (1),(2) vế theo vế,ta được:

\[
\begin{array}{l}
\,\frac{{a^3 }}{{1 + b}} + \frac{{b^3 }}{{1 + a}} \ge \left( {\frac{3}{2}a - \frac{1}{4}b - \frac{3}{4}} \right) + \left( {\frac{3}{2}b - \frac{1}{4}a - \frac{3}{4}} \right) \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\frac{5}{4}(a + b) - \frac{3}{2} \ge \frac{5}{4}.2\sqrt {ab} - \frac{3}{2}(AM - GM) = \,1\, \\
\end{array}
\] (vì ab=1)
Vậy Min P=1 khi a=b=1

Mong các bạn góp ý, nhận xét

Tìm giá trị nhỏ nhất của biểu thức:

$P = \frac{{a^2 }}{{b^2 + 1}} + \frac{{b^2 }}{{c^2 + 1}} + \frac{{c^2 }}{{a^2 + 1}}(a,b,c \ge 0\,\& \,a + b + c = 3)$

Mong các bạn có cách giải giúp mình, mình cũng đã nghĩ ra đc một cách, nhưng không hay lắm, khi nào rảnh mình post lên cho mọi người cùng trao đổi nhé !!!!

Mình có một cách như thế này, mong mọi người cho ý kiến ...
Biến đổi hệ đã cho, ta được:

$\left\{ \begin{array}{l}
x^3 - y^3 = x - y\,\,\,\,\,\,\,\,(1) \\
y^3 - z^3 = 4\left( {y - z} \right)\,\,(2) \\
z^3 - x^3 = 7\left( {z - x} \right)\,\,(3) \\
\end{array} \right.$
Cộng (1),(2),(3) vế theo vế, ta được:

$\begin{array}{l}
x - y + 4\left( {y - z} \right) + 7\left( {z - x} \right) = 0 \\
\Leftrightarrow \, - 6x + 3y + 3z = 0 \Leftrightarrow x = \frac{{y + z}}{2} \\
\end{array}$
Thế giá trị x vừa tìm được vào phương trình $x^2 + xy + y^2 = 1\,$ , và sau một vài phép biến đổi đơn giản, ta được:

$7y^2 + 4yz + z^2 = 4$
và kết hợp với phương trình đã cho: $y^2 + yz + z^2 = 4$
ta tiến hành trừ 2 phương trình trên vế theo vế, ta lại được: $\begin{array}{l}
6y^2 + 3yz = 0 \Leftrightarrow y(2y + z) = 0 \\
\Leftrightarrow \left[ \begin{array}{l}
y = 0 \\
y = \frac{{ - z}}{2} \\
\end{array} \right. \\
\end{array}$
Với y=0, dễ dàng tìm được các nghiệm (x;y;z) thỏa là (1;0;2);(-1;0;-2).
Với $y=\frac{-z}{2}$, ta thế vào phương trình $y^2 + yz + z^2 = 4$
và tìm được giá trị của z, từ đó suy ra nghiệm (x;y;z) thỏa là $\left( {\frac{{4\sqrt 3 }}{3};\frac{{ - 2\sqrt 3 }}{3};\frac{{\sqrt 3 }}{3}} \right);\left( {\frac{{ - 4\sqrt 3 }}{3};\frac{{2\sqrt 3 }}{3};\frac{{ - \sqrt 3 }}{3}} \right)$
Vậy pt có 4 nghiệm : (x;y;z)= (1;0;2);(-1;0;-2); $\left( {\frac{{4\sqrt 3 }}{3};\frac{{ - 2\sqrt 3 }}{3};\frac{{\sqrt 3 }}{3}} \right);\left( {\frac{{ - 4\sqrt 3 }}{3};\frac{{2\sqrt 3 }}{3};\frac{{ - \sqrt 3 }}{3}} \right)$

Mong các bạn cho ý kiến về lời giải này ....

Chứng minh rằng :

$\begin{array}{l}
\frac{{x^5 }}{{x^5 + y^2 + z^2 }} + \frac{{y^5 }}{{x^2 + y^5 + z^2 }} + \frac{{z^5 }}{{x^2 + y^2 + z^5 }} \ge \\
\frac{{x^2 }}{{x^5 + y^2 + z^2 }} + \frac{{y^2 }}{{x^2 + y^5 + z^2 }} + \frac{{z^2 }}{{x^2 + y^2 + z^5 }} \\
(x,y,z\, > 0\,\& \,xyz \ge 1) \\
\end{array}$

Mong các bạn giúp đỡ và cho ý kiến về bài tập này ....

Bài này cũng không khó lắm bạn ơi. Áp dụng 1 tí bất đẳng thức là ra thôi:

Với x<0 thì VP<0 còn VT>0, loại.
Suy ra x không âm.
Theo BĐT AM-GM, ta có:

$\begin{array}{l}
6\sqrt[3]{{4x^3 + x}} = 3\sqrt[3]{{4x(4x^2 + 1).2}} \le 4x + (4x^2 + 1) + 2 \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,4x^2 + 4x + 3 \\
\end{array}$ (1)
Đẳng thức xảy ra khi: x=0,5
Hiển nhiên, ta có bất đẳng thức sau:

$\begin{array}{l}
\left( {4x^2 - 1} \right)^2 + \left( {2x - 1} \right)^2 \ge 0 \\
\Leftrightarrow (16x^4 - 8x^2 + 1)\, + (4x^2 - 4x + 1) \ge 0 \\
\Leftrightarrow 16x^4 - 4x^2 - 4x + 2 \ge 0 \Leftrightarrow 16x^4 + 5 \ge 4x^2 + 4x + 3(2) \\
\end{array}$
Đẳng thức xảy ra khi x=0,5
Từ giả thiết và (1),(2) suy ra phương trình đã cho có nghiệm duy nhất: x=0,5

MỌI NGƯỜI CHO Ý KIẾN VÀ NHẬN XÉT NHÉ !!!!

Bài toán trên sử dụng một kĩ thuật khá hay, nhưng các bạn hãy thử sức với bài toán này, khá thú vị đó:
Tìm giá trị nhỏ nhất của biểu thức:

$P = \frac{{a^2 }}{{b^2 + 1}} + \frac{{b^2 }}{{c^2 + 1}} + \frac{{c^2 }}{{a^2 + 1}}(a,b,c \ge 0\,\& \,a + b + c = 3)$

Mong các bạn có cách giải giúp mình, mình cũng đã nghĩ ra đc một cách, nhưng không hay lắm, khi nào rảnh mình post lên cho mọi người cùng trao đổi nhé !!!!

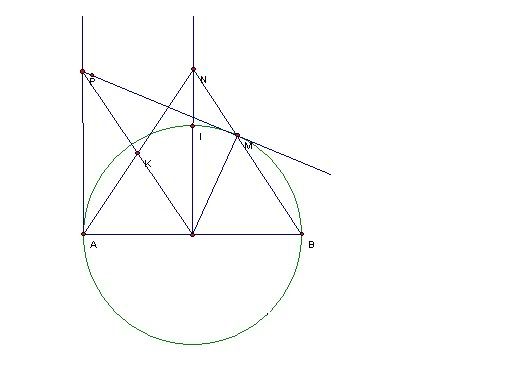
Dễ thấy,$\widehat{AMB} = \widehat{NOA} = 90^0 $
=> Tứ giác ANMO nội tiếp đường tròn đường kính AN.
=> $\widehat{KAM} = \widehat{NOM} = > \,\widehat{KAM} = \widehat{NOM}(vi`\widehat{KAM}\, = \widehat{KAM})$
Dễ dàng chứng minh được $\widehat{PMA} = \widehat{POM}$
=> $\widehat{IMK} = \widehat{IOK}$
=> Tứ giác IMOK nội tiếp=> $\widehat{IKO} = 180^0 - \widehat{IMO} = 90^0 $=> đpcm
[attachment=8995:HINH HOC.bmp]

ồ, câu d đơn giản mà bạn. Bạn chỉ cần chứng minh đẳng thức $TA^{2}=TC^{2}$. Và để chứng minh điều đó hoàn toàn đơn giản, bạn chì cần sử dụng một số tính chất đã học về góc, tứ giác nội tiếp, tam giác đồng dạng là ra ngay thôi..

Bài này cũng đơn giản thôi bạn ah`. Mình có một cách giải như thế này, bạn và mọi người tham khảo rồi cho ý kiến nhé!!!!!


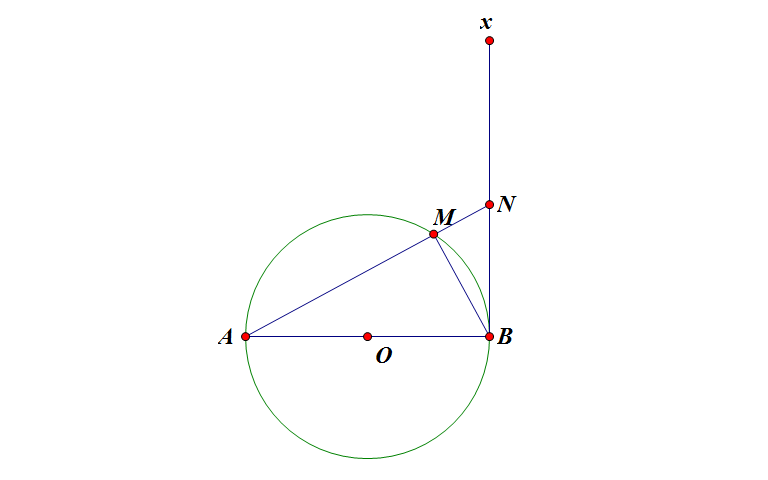
Dễ thấy $\widehat{AMB}=1V \Rightarrow AM.AN=AB^{2}$
$2AM+AN\geq 2\sqrt{2AM.AN}$$=> 2AM+AN\geq 2\sqrt{2}.AB$
Đẳng thức xảy ra khi: AN=2AM <=> M là điểm nằm chính giữa cung AB.
Vậy.....

Mình cũng hok bik nữa, hay là bạn thử đưa ra bài toán tổng quát xem, rồi mọi người cùng tham khảo. Bạn có cách giải nào khác cách giải của mình hok?????

bài này bạn áp dụng 1 tí bất đẳng thức Cauchy-Schwartz, ta được:
VT= $\frac{{{c^2}}}{{{c^2}(a + b)}} + \frac{{{a^2}}}{{{a^2}(b + c)}} + \frac{{{b^2}}}{{{b^2}(c + a)}} + \frac{{{{\left( {\sqrt[3]{{abc}}} \right)}^2}}}{{2abc}} \ge
\frac{{{{(a + b + c + \sqrt[3]{{abc}})}^2}}}{{{c^2}(a + b) + {a^2}(b + c) + {b^2}(c + a) + 2abc}}$.
Và ta dễ dàng chứng minh được:${c^2}(a + b) + {a^2}(b + c) + {b^2}(c + a) + 2abc = (a + b)(b + c)(c + a)$
Và từ đó, ta có đpcm.....

MONG CÁC BẠN GÓP Ý KIẾN VỀ LỜI GIẢI NÀY

Mấy bài này đơn khá đơn giản, chỉ cần áp dụng 1 tí BĐT Cauchy-Schwartz như trên, hoặc là bạn có cách giải sau:

Theo bất đẳng thức AM-GM, dễ dàng chứng minh được:
$\frac{{{a^2}}}{{a + b}} + \frac{{a + b}}{4} \ge a$
và hoàn toàn tương tự, xây dựng 3 bất đẳng thức nữa, rồi cộng các bất đẳng thức đó vế theo vế, ta được:
$\frac{{{a^2}}}{{a + b}} + \frac{{{b^2}}}{{b + c}} + \frac{{{c^2}}}{{c + d}} + \frac{{{d^2}}}{{d + a}} \ge \frac{{a + b + c + d}}{2} = \frac{1}{2}$
Hì,tuy không bằng Cauchy-Schwartz, nhưng cố gắng tìm cách giải khác là được rồi, hi`h`i...mong các bạn cùng vs quản lí cho ý kiến nhé

Bài 2: n=823543;m=352947;k=117649

Có thể là mình tính nhầm nhưng theo mình kết quả câu 3 là: y=x+23/15

Đặt $x^{2}$=y $\geq$ 0
Ta có, phương trình đã cho tương đương:

$\begin{array}{l}
\,\,\,\,\,\sqrt[5]{{27}}y^5 - 5y^3 + \sqrt[5]{{864}} = 0 \\
\Leftrightarrow \,\sqrt[5]{{27}}y^5 + \sqrt[5]{{864}} = 5y^3 \\
\end{array}$
Chia 2 vế của phương trình trên cho $\sqrt[5]{{27}}$ , ta được:

$\,\,\,\,y^5 + 2 = \frac{5}{{\sqrt[5]{{127}}}}y^3 $ (*)
X
Mặt khác, theo BĐT AM-GM (y không âm), ta có:

\[
\begin{array}{l}
\,\,\,\,y^5 + 2 = \,\frac{1}{3}y^5 + \frac{1}{3}y^5 + \frac{1}{3}y^5 + 1 + 1 \ge 5\sqrt[5]{{\frac{1}{3}y^5 .\frac{1}{3}y^5 .\frac{1}{3}y^5 .1.1}} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\frac{5}{{\sqrt[5]{{127}}}}y^3 \\
\end{array}
\]
Đẳng thức xảy ra khi y=\[\sqrt[5]{3}\]
Kết hợp với (*), ta suy ra y=\[\sqrt[5]{3}\]
Do đó, x=\[
\pm \sqrt {\sqrt[5]{3}}
\]
Vậy phương trình có 2 nghiệm:x=\[
\pm \sqrt {\sqrt[5]{3}}
\]

Kết quả:
D-B=6.9h
E=6
F=0
S=59.1

Bài bất đẳng thức, ngoài cách dùng AM-GM như của bạn Ispectorgadget, mình cũng có một cách khác, cách này dùng Cauchy-Schwartz:
và thật dễ dàng, theo Cauchy-Schwartz, ta có:
$VT \ge \frac{{\left( {x + y + z} \right)^2 }}{{x + y + z + 3}}$

Đến đây, ta đặt $t=x+y+z(t>0)$, dễ thấy$t \ge 3$
Và hiển nhiên, ta có bất đẳng thức
$(t - 3)(2t + 3) \ge 0$
Từ đó suy ra, $$\frac{{t^2 }}{{t + 3}} \ge \frac{3}{2}$$
Và ta có ngay, VT$\ge \frac{3}{2}$
(đpcm)

MOD: Lần sau chú ý hơn cách trình bày.

bạn làm rõ chỗ mà câu 1 ý, áp dụng Cauchy-Schwartz xong rồi,nhưng còn bậc 3 của a,b,c nữa mà, bạn phải làm rõ ra chứ, nhỡ đâu ...