Trên kho chia sẻ file me zing của mình


Giải tích 2-Jean Marie Monier

Đại số 2-Jean Marie Monier

Max thì dễ rồi ( ) theo lời giải của thầy Thế $M(k)=10^{k-1}$
Bài toán chỉ còn phải tìm min

Với $k=1$ dễ thấy $m(1)=1$
Với $k=2$ cũng vậy $m(2)=\dfrac{19}{10}$
Với $k=3$ thì $m(3)=\dfrac{199}{19}$
Mấy cái trên cũng không khó khăn lắm để kiểm tra . Tuy nhiên chớ có vội mừng ...

Với $k=4$ thì $m(4)=\dfrac{1099}{19}$ cơ!
Ta sẽ chứng minh bằng quy nạp rằng

$m(k)=\mathop\min\limits_{\left\{10^{k-1}\le n\le 10^k-1\right\}}\dfrac{n}{s(n)}=\dfrac{10^{k-1}+10^{k-2}-1}{9k-17}\qquad(k\ge 4)$

Bài giải của chú hxthanh đã sai!

Giá trị $m(k)$ ở trên đạt được khi n có dạng $1099....9$

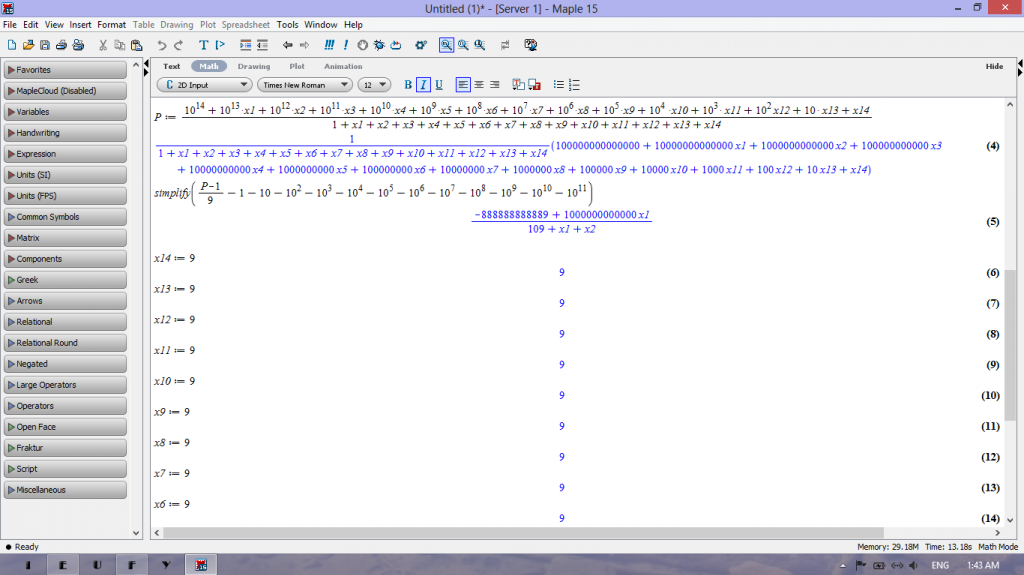
nhưng với thuật toán em đang làm thì chẳng hạn với $k=15 $, $m(15)$ xảy ra khi $n=100999999999999$ như trong minh họa hình bên dưới, dễ dàng thấy rằng

$\dfrac{100999999999999}{109}<\dfrac{109999999999999}{118} $

Ngày mai em sẽ post lời giải 3 trang cho bài này sau.

Em nhận định rất đúng!
Ban đầu tôi đã đưa ra thuật toán tính số các số $0$ ngay sau số $1$ là
$\left\lfloor\log_{10}(9k)\right\rfloor$
Nhưng thử lại thấy cái này không đúng với $k=12$
Do đó tôi mới đặt ra giả thiết rằng $k\ge 4$ thì $m(k)$ xảy ra tại $n=1099...$
Rồi cố gắng tìm cách quy nạp, nhưng quả thực nó có vấn đề...
Vì vậy ...

Nếu em không sai sót thì

$m(k)$ xảy ra tại $n=100....999$ có $k-M-2$ số 0

Với $M=\max \{ x \in \mathbb{N}, x.10^x \le \dfrac{10^{k-1}-1}{9} \}$

Tổng quát:
Với mỗi số nguyên dương $n$ có $k$ chữ số $(k>1)$, gọi $s(n)$ là tổng các chữ số của $n$ trong hệ thập phân.
Ứng với mỗi $k>1$, gọi
$$M(k) = \max \left \{ \frac{n}{s(n)}|{10^{k-1} \leq n \leq 10^k-1}\right \};$$
$$m(k) = \min \left \{ \frac{n}{s(n)} | {10^{k-1} \leq n \leq 10^k-1}\right \}$$

Có thể biểu diễn $M(k), m(k)$ theo $k$ hay không?

Giả sử n có dạng $ \overline{a_1a_2...a_k} $ , $ a_1;a_2;..;a_k \in \{0;1;...;9\} ,a_1>0 $

Xét $ P=\dfrac{n}{s(n)}=\dfrac{10^{k-1}a_1+10^{k-2}a_2+...+a_k}{a_1+a_2+...+a_k} \; \; (*)$


$ (*) \Leftrightarrow 0= \sum_{i=1}^k (10^{k-i}-P)a_i \le (10^{k-1}-P) \sum_{i=1}^k a_i$

Do $\sum_{i=1}^k a_i >0 $ nên phải có $ P \le 10^{k-1}$

Cho $a_i=0 \; \forall i>1 $ , khi đó $ P=\dfrac{10^{k-1}a_1}{a_1}=10^{k-1} $

Do đó $ Max P=10^{k-1} $ hay

$$M(k) =10^{k-1} $$


Đặt $ x_i=\frac{a_{i+1}}{a_1} \; , i \in \{1;2...;k-1\} $ và quy ước $x_i =0 ,\;\forall i \le 0 $

$ \Rightarrow 0 \le x_i \le 9 \; , \forall i \in \{1;2...;k-1\} $

Khi đó, $P=\dfrac{10^{k-1}+10^{k-2}x_1+...+x_{k-1}}{1+x_1+x_2+...+10x_{k-2}+x_{k-1}}$

$ \Leftrightarrow P-1= \dfrac{10^{k-1}-1+(10^{k-2}-1)x_1+...+9x_{k-2}}{1+x_1+x_2+...+x_{k-1}} $

Với $k=2 $

$P-1=\dfrac{9}{1+x_1} \ge \dfrac{9}{10} $

$ \Leftrightarrow P \ge \dfrac{19}{10} $, dấu bằng xảy ra khi $n=19 $

Với $ k>2 $

$ P-1 \ge \dfrac{10^{k-1}-1+(10^{k-2}-1)x_1+...+(100-1)x_{k-3}+9x_{k-2}}{10+x_1+x_2+...+x_{k-2}} $

$ \Leftrightarrow \dfrac{P-1}{9} \ge \dfrac{\frac{10^{k-1}-1}{9}+\frac{10^{k-2}-1}{9} x_1+...+11x_{k-3}+x_{k-2}}{10+x_1+x_2+...+x_{k-2}}$

$ \Leftrightarrow \dfrac{P-1}{9}-1 \ge \dfrac{\frac{10^{k-1}-1}{9}-10+\frac{10^{k-2}-10}{9}x_1+...+10x_{k-3}}{10+x_1+x_2+...+x_{k-2}} \ge \dfrac{\frac{10^{k-1}-1}{9}-10+\frac{10^{k-2}-10}{9}x_1+...+110x_{k-4}+10x_{k-3}}{19+x_1+x_2+...+x_{k-3}} \;\; (**) $

Với $k=3$

$\dfrac{P-1}{9}-1 \ge \dfrac{1}{19} $

$\Leftrightarrow P \ge \frac{199}{19} $ , dấu bằng xảy ra khi $n=199$

Nếu ai có Maple thì dễ dàng thấy được trường hợp $k=2;3$ thì quy luật $n_0$ thỏa $m(k)$ có dạng giống nhau và tính chất đã thay đổi kể từ khi $k \ge 4 $ và thuật toán sau sẽ lý giải cho điều khác biệt đó


Với $k>3 $ , đặt $ k=3+m \; , m \ge 1$ ( ngồi 2 ngày để tạo ra chỗ này nên cứ xem tiếp đã rồi hãy thắc mắc )

$(**) \Leftrightarrow \dfrac{P-1}{9}-1 \ge \dfrac{\frac{10^{m+2}-1}{9}-10+\sum_{i=1}^{m} \frac{10^{m+2-i}-10}{9} x_i}{10+9+\sum_{i=1}^{m}x_i} \;\;\; (***)$

Xét khi m rất lớn ( mục đích là để khi thực hiện p bước thuật toán $\Delta $ dưới đây ta vẫn thu được bất đẳng thức đúng ( vì p khá nhỏ so với m nên hệ số tự do trên tử thức dương)! )

Hệ số của $x_m$ trên tử thức là $10$, do đó

$ \dfrac{P-1}{9}-1-10 \ge \dfrac{\frac{10^{m+2}-1}{9}-10-10(10+9)+\sum_{i=1}^{m-1} \frac{10^{m+2-i}-100}{9}x_i}{10+9+\sum_{i=1}^mx_i} $

$\ge \dfrac{\frac{10^{m+2}-1}{9}-10-10(10+9)+\sum_{i=1}^{m-1} \frac{10^{m+2-i}-10^2}{9} x_i}{10+2.9+\sum_{i=1}^{m-1}x_i}$

do $\dfrac{10^{m+2}-1}{9}-10-10(10+9) >0 $ vì m rất lớn và $ x_m \le 9$.


Hệ số của $x_{m-1} $ trên tử thức là $10^2 $, do đó

$ \dfrac{P-1}{9}-1-10-10^2 \ge \dfrac{\frac{10^{m+2}-1}{9}-10-10(10+9)-10^2(10+2.9) +\sum_{i=1}^{m-2} \frac{10^{m+2-i}-10^3}{9} x_i}{10+2.9+\sum_{i=1}^{m-1}x_i} $

$\ge \dfrac{\frac{10^{m+2}-1}{9}-10-10(10+9)-10^2(10+2.9)+\sum_{i=1}^{m-2} \frac{10^{m+2-i}-10^3}{9}x_i}{10+3.9+\sum_{i=1}^{m-2}x_i}$

do $\frac{10^{m+2}-1}{9}-10-10(10+9)-10^2(10+2.9) >0 $ vì m rất lớn và $x_{m-1} \le 9$ .


Đến đây ta đã dần thấy quy luật sau 2 bước của thuật toán sau:

Gọi $\Delta_p$ là bước thứ p của thuật toán $\Delta$ trừ hai vế của bất đẳng thức $(***)$ cho $10^p$ và cho $x_{m-p}=9 $

Ta chứng minh sau p bước ($\frac{10^{m+2}-1}{9} \ge \sum_{i=0}^p 10^i(10+9i)$) thực hiện $\Delta$ , ta thu được bất đẳng thức đúng là:

$\dfrac{P-1}{9}-\sum_{i=0}^p 10^i \ge \dfrac{\frac{10^{m+2}-1}{9}-\sum_{i=0}^p 10^i(10+9i) +\sum_{i=1}^{m-p}\frac{10^{m+2-i}-10^{p+1}}{9}x_i}{10+9(p+1)+\sum_{i=1}^{m-p}x_i} $

Với $p=1;p=2 $ ta đã chứng minh ở trên. Giả sử thu được bất đẳng thức đúng sau khi thực hiện $p$ bước (p thỏa $\frac{10^{m+2}-1}{9} \ge \sum_{i=0}^{p+1} 10^i(10+9i)$), thực hiện trừ 2 vế của bdt cho $10^{p+1} $ ta được bdt :

$\dfrac{P-1}{9}-\sum_{i=0}^{p+1} 10^i \ge \dfrac{\frac{10^{m+2}-1}{9}-\sum_{i=0}^p 10^i(10+9i)-10^{p+1}(10+9(p+1)) +\sum_{i=1}^{m-p-1}( \frac{10^{m+2-i}-10^{p+1}}{9}-10^{p+1}) x_i}{10+9(p+1)+\sum_{i=1}^{m-p}x_i} $

$ \ge \dfrac{\frac{10^{m+2}-1}{9}-\sum_{i=0}^{p+1} 10^i(10+9i) +\sum_{i=1}^{m-p-1}\frac{10^{m+2-i}-10^{p+2}}{9}x_i}{10+9(p+1)+\sum_{i=1}^{m-p}x_i} $

$ \ge \dfrac{\frac{10^{m+2}-1}{9}-\sum_{i=0}^{p+1} 10^i(10+9i) +\sum_{i=1}^{m-p-1}\frac{10^{m+2-i}-10^{p+2}}{9}x_i}{10+9(p+2)+\sum_{i=1}^{m-p-1}x_i} $

do $\frac{10^{m+2}-1}{9}-\sum_{i=0}^{p+1} 10^i(10+9i) >0 $ và $ x_{m-p} \le 9 $

Ta vừa thu được một bất đẳng thức đúng và đây chính là bất đẳng thức thu được với bước $\Delta_{p+1} $

Vậy sau p bước thuật toán $\Delta$ với điều kiện $ \frac{10^{m+2}-1}{9} \ge \sum_{i=0}^p 10^i(10+9i) $ thì ta thu được bất đẳng thức đúng là


$$\dfrac{P-1}{9}-\sum_{i=0}^p 10^i \ge \dfrac{\frac{10^{m+2}-1}{9}-\sum_{i=0}^p 10^i(10+9i) +\sum_{i=1}^{m-p}\frac{10^{m+2-i}-10^{p+1}}{9}x_i}{10+9(p+1)+\sum_{i=1}^{m-p}x_i} \;\;\;(****)$$


Ta có: $\sum_{i=0}^p 10^i(10+9i) =\sum_{i=0}^p 10^i (1+9(i+1) )= \sum_{i=0}^p 10^i +9 \sum_{i=0}^p (i+1) 10^i$

Dễ thu gọn được :

$\sum_{i=0}^p 10^{i}=\dfrac{10^{p+1}-1}{9} $

$9 \sum_{i=0}^p (i+1) 10^i = \dfrac{(p+1)10^{p+2}-(p+2)10^{p+1}+1}{9} $ ( Xét đạo hàm hàm $\sum_{i=0}^p x^{i+1} $ )

Vậy : $\sum_{i=0}^p 10^i(10+9i)=(p+1)10^{p+1} $

Do đó


$$(****) \Leftrightarrow \dfrac{P-1}{9}-\dfrac{10^{p+1}-1}{9} \ge \dfrac{\frac{10^{m+2}-1}{9}-(p+1)10^{p+1} +\sum_{i=1}^{m-p}\frac{10^{m+2-i}-10^{p+1}}{9}x_i}{10+9(p+1)+\sum_{i=1}^{m-p}x_i}$$


Để tìm điểm dừng trong thuật toán, ta phải giải phương trình ẩn p

$\frac{10^{m+2}-1}{9}-(p+1)10^{p+1} \ge 0 $


Đặt $ D=\{ x \in \mathbb{N}, \dfrac{10^{m+2}-1}{9} \ge (x+1) 10^{x+1} \} $

Dễ thấy $ D \neq \varnothing $ vì $ 0 \in D $ $ \Rightarrow \exists p_0=\max D$


Đặt $ A_j=[\dfrac{10^{j+1}-1}{9}+j; \dfrac{10^{j+2}-1}{9}+j] \;\;, j \in \mathbb{N}$ , $ B_j=(\dfrac{10^{j+1}-1}{9}+j; \dfrac{10^{j+2}-1}{9}+j) \;\;, j \in \mathbb{N} $

Dễ thấy rằng $ \cup_{j \in \mathbb{N}} A_j=\mathbb{N}^* $ , do đó $ \exists j \in \mathbb{N}, m \in A_j $

$\forall j_1 \neq j_2 \Rightarrow B_{j_1} \cap B_{j_2}=\varnothing $

do đó, với $m \in \mathbb{N}^* $ cố định cho trước, tồn tại duy nhất $j \in \mathbb{N} $ sao cho $\dfrac{10^{j+1}-1}{9}+j \le m \le \dfrac{10^{j+2}-1}{9}+j $

Với j thỏa điều kiện trên, ta có tính chất ( chưa CM ) : $ p_0=m-j-1 $


Cách khác, sử dụng hàm Lambert , $x=W(x) e^{W(x)} $

Dễ dàng giải được: $ p_0=\left \lfloor \dfrac{\mathbf{W}(\frac{10^{m+2}-1}{9}\ln 10)}{\ln 10} \right \rfloor -1$

Vậy , sau $p_0$ bước thuật toán $\Delta $, ta được bất đẳng thức

$$\dfrac{P-1}{9}-\dfrac{10^{p_0+1}-1}{9} \ge \dfrac{\frac{10^{m+2}-1}{9}-(p_0+1)10^{p_0+1} +\sum_{i=1}^{m-p_0}\frac{10^{m+2-i}-10^{p_0+1}}{9}x_i}{10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i}$$


$\Leftrightarrow \dfrac{P-1}{9}-\dfrac{10^{p_0+2}-1}{9} \ge \dfrac{\frac{10^{m+2}-1}{9}-(p_0+2)10^{p_0+2} +\sum_{i=1}^{m-p_0-1}\frac{10^{m+2-i}-10^{p_0+2}}{9}x_i}{10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i} $

$\Leftrightarrow P-10^{p_0+2} \ge \dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2} +\sum_{i=1}^{m-p_0-1} (10^{m+2-i}-10^{p_0+2})x_i}{10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i} $

Đặt $f(x_1;x_2;...;x_{m-p_0})=\dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2} +\sum_{i=1}^{m-p_0-1} (10^{m+2-i}-10^{p_0+2})x_i}{10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i} $


$f_{x_1}^{'}(x_1;x_2;...;x_{m-p_0}) $

$=\dfrac{(10^{m+1}-10^{p_0+2})(10+9(p_0+1)+\sum_{i=2}^{m-p_0}x_i)-10^{m+2}+1+9(p_0+2)10^{p_0+2}-\sum_{i=2}^{m-p_0-1} (10^{m+2-i}-10^{p_0+2})x_i}{(10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i)^2}$


$ \ge \dfrac{(10^{m+1}-10^{p_0+2})(10+9(p_0+1)+\sum_{i=2}^{m-p_0}x_i)-10^{m+2}+1+9(p_0+2)10^{p_0+2}-(10^{m+1}-10^{p_0+2})\sum_{i=2}^{m-p_0-1} x_i}{(10+9(p_0+1)+\sum_{i=1}^{m-p_0}x_i)^2} $


$\ge 0$

Do đó,

$f(x_1;x_2;...;x_{m-p_0})$

$\ge f(0;x_2;...;x_{m-p_0})=\dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2} +\sum_{i=2}^{m-p_0-1} (10^{m+2-i}-10^{p_0+2})x_i}{10+9(p_0+1)+\sum_{i=2}^{m-p_0}x_i} $

$f(x_1;x_2;...;x_{m-p_0}) $ và $f(0;x_2;..;x_{m-p_0}$ có cùng dạng như nhau nên sau khi thực hiện $m-p_0-1$ các bước xét sự biến thiên hàm f theo lần lượt các biến $x_i \;\;\;, i \in \{1;2;...;m-p_0-1\} $

ta thu được

$f(x_1;x_2;...;x_{m-p_0}) \ge f(0;0;..;0;x_{m-p_0}) =\dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2}}{10+9(p_0+1)+x_{m-p_0}}$


$\ge \dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2}}{10+9(p_0+1)} $

$\Rightarrow P-10^{p_0+2} \ge \dfrac{10^{m+2}-1-9(p_0+2)10^{p_0+2}}{10+9(p_0+1)} $


$$P \ge \dfrac{10^{m+2}+10^{p_0+2}-1}{9p_0+19} $$

$$\Leftrightarrow {\color{DarkBlue} {P \ge \dfrac{10^{k-1}+10^{p_0+2}-1}{9p_0+19}}} $$

Dấu bằng xảy ra khi $ x_1=...=x_{m-p_0}=0 \;\;, x_{m-p_0+1}=...=x_{k-1}=9 $

hay ${\color{DarkBlue} {m(k)=\dfrac{10^{k-1}+10^{p_0+2}-1}{9p_0+19}} }$

đạt được khi $n=\overline{10..09..9}$ có $ k-p_0-3$ số 0 và $p_0+2$ số 9

Có một điều thú vị là công thức $m(k)$ ở trên đúng với mọi k nguyên dương, tức:



$$m(k)=\dfrac{10^{k-1}+10^{\left \lfloor \dfrac{\textbf{W}(\frac{10^{k-1}-1}{9}\ln 10)}{\ln 10} \right \rfloor +1}-1}{9\left \lfloor \dfrac{\textbf{W}(\frac{10^{k-1}-1}{9}\ln 10)}{\ln 10} \right \rfloor +10} \;\;\; ,\forall k \in \mathbb{N}^* $$


Bài giải có vẻ khủng bố nhưng kết quả thì chắc đúng rồi. Đã test với Maple !

Thế là đi tông 2 ngày mà không biết có được 10đ không nữa

Vẫn tiếp tục tìm công thức tường minh cho $p_0$...

Cuối cùng tôi cũng tìm thấy một quy luật đáng tin cậy sau:
\begin{array}{|c|}
\hline\\
\text{Đặt $k_i=\dfrac{10^{i+1}+9i+17}{9}$ với $i=-1,0,1,2,...$}\\
\text{Với $k_{i-1}< k\le k_i$ ta có: $m(k)=\dfrac{10^{k-1}+10^{k-1-i}-1}{9(k-1-i)+1}$}\\
\text{đạt được tại $n=10..09...9$ với $i$ số $0$}\\
\hline
\end{array}
...
Xuất phát từ việc tìm dãy nghiệm nguyên lớn nhất của dãy bất phương trình

$\dfrac{10^{k-1}+10^{k-1}-1}{9(k-1)+1}<\dfrac{10^{k-1}+10^{k-2}-1}{9(k-2)+1}<\dfrac{10^{k-1}+10^{k-3}-1}{9(k-3)+1}<...<\dfrac{10^{k-1}+10^{k-1-i}-1}{9(k-1-i)+1}<...$

Em nghĩ phải thế này mới đúng ( vì trong đáp án của chú..i có thể âm kìa !)


\begin{array}{|c|}
\hline\\
\text{Đặt $k_i=\dfrac{10^{i}+9i+8}{9}$ với $i=0,1,2,...$}\\
\text{Với $k_{i}< k\le k_{i+1}$ ta có: $m(k)=\dfrac{10^{k-1}+10^{k-1-i}-1}{9(k-1-i)+1}$}\\
\text{đạt được tại $n=10..09...9$ với $i$ số $0$}\\
\hline
\end{array}

Kết quả này hoàn toàn trùng khớp với kết quả $p_0=m-j-1$ như trong bài của em, số chữ số 0 là $m-p_0=j+1$

cho đa thức P(x) và Q(x)=aP(x)+bP'(x)+cP''(x) với a,b,c thuộc R,a khác 0,b^2-4ac >0.cmr nếu Q(x) vô nghiệm thì P(x) vô nghiệm

Ở đây, đúng ra phải thêm một ý: $P ,Q \in R[x] $ và ta chỉ xét đến nghiệm thực của các đa thức !

Một tương đương logic ai cũng biết:

$Q(x)$ vô nghiệm thì $P(x)$ vô nghiệm $\Leftrightarrow$ $P(x)$ có nghiệm thì $Q(x)$ có nghiệm..

Nếu $P(x)$ là đa thức bậc lẻ thì $Q(x)$ cũng bậc lẻ nên cả hai đều có nghiệm thực.

Nếu $deg P=2n \;\;, n \in \mathbb{N}^* $ và $P(x)$ có $k$ nghiệm (kể cả bội)

Do P bậc chẵn nên nếu có nghiệm thì có một số chẵn nghiệm (kể cả bội), do đó, số nghiệm của $P(x)$ bằng $2m \;\;,m \in \mathbb{N}^* $ (kể cả bội)

Xét phương trình $a P(x)+b P^{'}(x)+cP^{''}(x)=0 $ $\Leftrightarrow P(x)+\dfrac{b}{a}P^{'}(x)+\dfrac{c}{a}P^{''}(x) =0$

Thấy rằng : $b^2 >4ac \Leftrightarrow \dfrac{b^2}{a^2}>4 \dfrac{c}{a} $

Đặt $u=\dfrac{b}{a} \;\;, v=\dfrac{c}{a} $ $\Rightarrow u^2>4v $

Ta cần CM: $ P(x)+uP^{'}(x)+vP^{''}(x)=0 $ có nghiệm.

Gọi $u_1,v_1$ là hai số thực khác 0 bất kỳ.


Xét $H_1(x)=e^{\frac{x}{u_1}}P(x) $ $ \Rightarrow H_1(x) $ có $2m$ nghiệm thực (kể cả bội)

$\Rightarrow H_1^{'}(x)=\dfrac{e^{\frac{x}{u_1} }}{u_1}(P(x)+u_1 P^{'}(x)) $ có ít nhất $2m-1$ nghiệm (kể cả bội)

$\Rightarrow P(x)+u_1 P^{'}(x) $ có ít nhất $2m-1$ nghiệm (kể cả bội)

$\Rightarrow P(x)+u_1P^{'}(x)=\prod_{i=1}^{2m-1}(x-x_i) R_{2n-2m+1}(x) $, với $R_{2n-2m+1}(x)$ là đa thức bậc $2n-2m+1$, tức bậc lẻ, nên $R_{2n-2m+1} $ có ít nhất một nghiệm.

Vậy $P(x)+u_1 P^{'}(x) $ có ít nhất $2m$ nghiệm (kể cả bội)

Xét $H_2(x)=e^{\frac{x}{v_1}}(P(x)+u_1P^{'}(x) )$

Tương tự như trên ta cũng có: $P(x)+u_1P^{'}(x)+v_1(P^{'}(x)+u_1P^{''}(x) $ có ít nhất $2m$ nghiệm thực (kể cả bội)

hay $P(x)+(u_1+v_1)P^{'}(x)+u_1v_1P^{''}(x) $ có ít nhất $2m$ nghiệm thực (kể cả bội).

Do $u^2-4v>0 $ nên phương trình $x^2-ux+v=0 $ có 2 nghiệm phân biệt $x_1;x_2 $

Chọn $u_1=x_1\;, v_1=x_2 $,

$ \Rightarrow P(x)+uP^{'}(x)+vP^{''}(x) $ có ít nhất $2m$ nghiệm hay $Q(x)$ có nghiệm.

Vậy có đpcm.

Tông quát:
Nếu đa thức $a_nx^n+a_{n-1}x^{n-1}+...+a_0$ (với $a_i$ nguyên) có n nghiệm và $Q(x)=a_n.P(x)+a_{n-1}.P'(x)+...+a_0.P^{(n)}(x)$ vô nghiệm thì $P(x)$ vô nghiệm.

Việc tổng quát thế này không có ý nghĩa cho lắm, vì thực tế, việc chứng minh $Q(x)=a_n.P(x)+a_{n-1}.P'(x)+...+a_0.P^{(n)}(x)$ vô nghiệm dài dòng và cồng kềnh hơn rất nhiều so với việc tìm nghiệm $P(x)$. Theo lời giải của mình trên kia, ta sẽ đi từ từ để đến với một mệnh đề nho nhỏ.

Xét $R(x)=\sum_{i=0}^n a_i x^i \in R[x] \;\;, n \in \mathbb{N}^*\;,a_n \neq 0$ có $n$ nghiệm thực $x_i $. ( không nhất thiết phân biệt)

Với $P \in R[x] $ bậc $2m \in \mathbb{N}^* , 2m \ge n$ có ít nhất $2k\;, k\in \mathbb{N}^*$ nghiệm thực (kể cả bội)

Như trong bài giải ở trên , ta có tính chất nhỏ là $\forall t \in \mathbb{R} , P(x)+t.P'(x) =0$ có ít nhất $2k$ nghiệm thực kể cả bội.

Xét dãy $ \begin{cases} H_1(x)=P(x)-x_1.P'(x) \\H_i(x)=H_{i-1}(x)-x_i.H_{i-1}'(x) \;\;\;, i \ge 2 \end{cases} $

Dễ chứng minh được rằng, $H_i(x)$ có ít nhất $2k$ nghiệm kể cả bội $\forall i \in \{1;2;...;n\} $

Với $i \in \{1;2;...;n \} $

Gọi $ E_{ij} = \sum_{1 \le i_1<i_2<...<i_j \le i} x_{i_1}x_{i_2}...x_{i_j} \;\;\;, j \in \{1;2...;i \}$ là đa thức đối xứng sơ cấp thứ $j$


Tính cụ thể các $H_2;H_3$ ta dễ tổng quát và chứng minh quy nạp rằng:

$H_i(x)=P(x)+\sum_{j=1}^i (-1)^jE_{ij} P^{(j)}(x)$

Vậy, $H_n(x)=P(x)+\sum_{j=1}^n (-1)^jE_{nj}P^{(j)}(x) $

Theo định lý Viète , $E_{nj} =(-1)^j\dfrac{a_{n-j}}{a_n} $

$\Rightarrow H_n(x)=P(x)+ \sum_{j=1}^n \dfrac{a_{n-j}}{a_n} P^{(j)}(x) $

Từ $H_n(x)$ có ít nhất $2k$ nghiệm thực kể cả bội

$\Rightarrow a_n P(x)+\sum_{j=1}^n a_{n-j} P^{(j)}(x) $ có ít nhất $2k$ nghiệm thực kể cả bội

Tóm lại, ta vừa chứng minh rằng : Với đa thức hệ số thực $\sum_{i=0}^n a_i x^i $ bậc $n$ có $n$ nghiệm thực (không nhất thiết phân biệt) và $P(x) $ là đa thức hệ số thực bậc chẵn không nhỏ hơn $n$ ,có ít nhất $2k$ nghiệm thực (kể cả bội), thế thì

$ \sum_{i=0}^n a_{n-i}P^{(i)}(x) =0$ cũng có ít nhất $2k$ nghiệm thực kể cả bội. ($P^{(0)}(x)=P(x) $)

Cho $C$ là một điểm nằm trên đường kính $AB$ của nửa đường tròn tâm $O$, khác $A,B,O$. Hai tia vuông góc với nhau qua $C$ cắt nửa đường tròn tại $D,E$. Đường thẳng qua $D$ vuông góc với $DC$ cắt lại đường tròn tại $K$. Chứng minh rằng nếu $K$ không trùng $E$ thì $KE$ song song $AB$

Một chuyện hy hữu là...kết luận của bài toán đã sai!

Cụ thể, ta có thể vẽ ngay cái hình, tuy nhiên, nếu muốn có chứng minh chặt chẽ thì chẳng hạn...

Ta sẽ chỉ ra cách dựng một trường hợp thỏa giả thiết.

Sau khi đã có $AB$ và nửa đường tròn $(O)$ bán kính $R$. Vẽ đường thẳng d song song với $AB$ và cách $AB$ một đoạn nhỏ hơn $\dfrac{R}{2}$ cắt nửa đường tròn tại $D$ và $E$.

Gọi $I$ là trung điểm $DE$.

Do $ID^2+IO^2=OD^2=R^2 \Rightarrow ID=\sqrt{R^2-OI^2}>\dfrac{\sqrt{3}}{2}R>\dfrac{R}{2}>OI$

$\Rightarrow AB$ cắt đường tròn tâm $I$ bán kính $ID$ tại hai điểm nằm trong đoạn $AB$ đồng thời khác $A;B;O$, chọn một trong hai điểm đó gọi là $C$. Hiển nhiên $\Delta DCE$ vuông tại $C$.

Vậy, các điểm $C;E;D$ thỏa mãn giả thiết đề bài.

Tiếp tục, theo giả thiết đề bài, dựng đường thẳng vuông góc với $CD$ tại $D$ cắt đường tròn tâm $O$ tại $K$ . Hiển nhiên, $DK // CE $ nên $K$ không thuộc $DE$, tức

$KE$ không song song $AB$ vì $DE //AB$

Tìm $f:R \rightarrow R$ liên tục tại $0$ thoả $$ f(2x)=f(x)\cos{x}$$

Hic. Cái đề thi giữa kỳ năm I của mình sao gặp hoài vậy ta @@

Từ giả thiết

$f(x) = f\left( \dfrac{x}{2} \right) \cos\left( \dfrac{x}{2} \right) = f\left( \dfrac{x}{4} \right) \cos\left( \dfrac{x}{2} \right) \cos\left( \dfrac{x}{4} \right) =\cdots= f\left( \dfrac{x}{2^n} \right) \prod\limits_{i=1}^n \cos \dfrac{x}{2^i}, \; \forall n \in \mathbb{N}^* $

$\Leftrightarrow 2^n \sin \left( \dfrac{x}{2^n} \right) f(x) = f\left( \dfrac{x}{2^n} \right) \sin x $

$\Leftrightarrow x \dfrac{\sin \dfrac{x}{2^n}}{\dfrac{x}{2^n}} f(x) = f\left( \dfrac{x}{2^n}\right) \sin x $

Cho $n \rightarrow + \infty $ và do $f$ liên tục tại 0 nên

$ x f(x)=f(0) \sin x $

Thử lại $ f(x)= a \dfrac{\sin x}{x} ,\; a \in \mathbb{R} $ thỏa mãn đề bài

theo mình thì ở quy tắc 1 cần sửa lại là giới hạn của f(x) và g(x) khi x->x0 đều bằng 0.

Nếu $\lim_{x \to x_0} g(x) \neq 0$ thì $\lim_{x \to x_0} \dfrac{f(x)}{g(x)} $ không phải dạng vô định nên giới hạn tính được một cách bình thường không cần gì $L'Hospital$ . Tuy nhiên, dùng $L'Hospital$ cũng chẳng sai nếu $\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)} $ tồn tại hữa hạn.

Nói chung Hospital là sử dụng đạo hàm thoải mái cho đến kh ra đáp số! He he
Nó còn áp dụng cho cả các dạng $0^0, 1^{\infty}$

Còn bài em hỏi không thuộc dùng Hos do $x \to \infty$
______________
Đi nấu cơm cái, có gì lát anh giải bài giới hạn này dùm cho!

Đây là cái lỗi mà rất rất nhiều sinh viên mắc phải, thậm chí nhiều em học sinh PT cũng ham hố xài cho bằng được khi không hiểu rõ định lý.
Cứ đạo hàm..rồi đạo hàm là sẽ ra? Không !

Ví dụ:

Xét bài làm:

$\lim_{x \to +\infty } \dfrac{x}{x+sin(x)}=\lim_{x \to +\infty} \dfrac{1}{1+cos(x)} = ? $

Rõ ràng $\lim_{x \to +\infty} \dfrac{1}{1+cos(x)} $ không tồn tại ! Nhưng lại có :

$\lim_{x \to +\infty } \dfrac{x}{x+sin(x)}=\lim_{x \to +\infty} \dfrac{1}{1+\frac{\sin x}{x}}=1 $


Để vận dụng định lý rất hữu dụng $L'Hospital $ , ta cần nắm rõ bản chất của nó.

Như phát biểu của haiphong08 .

Xét $f(x),g(x)$ liên tục trên $U_{\epsilon x_0}$ là một $\epsilon$ lân cận của $x_0$ và khả vì trên $U_{\epsilon x_0}-\{x_0\}$

Theo định lý Cauchy, cho x cố định, luôn tồn tại $\eta_x$ nằm giữa $x $và $x_0$ sao cho

$\dfrac{f(x)-f(x_0)}{g(x)-g(x_0)}=\dfrac{f'(\eta_x)}{g'(\eta_x)}$

Vậy : $\lim_{x \to x_0} \dfrac{f(x)-f(x_0)}{g(x)-g(x_0)}=\lim_{\eta_x \to x_0}\dfrac{f'(\eta_x)}{g'(\eta_x)} $

Do đó, nếu $\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)} =l$ hữu hạn thì.. $\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)}=\lim_{\eta_x \to x_0}\dfrac{f'(\eta_x)}{g'(\eta_x)}$

$\lim_{x \to x_0} \dfrac{f(x)-f(x_0)}{g(x)-g(x_0)}=\lim_{\eta_x \to x_0}\dfrac{f'(\eta_x)}{g'(\eta_x)} =\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)}=l$

Nếu $\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)} $ không tồn tại, thì có thể $\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)} \neq \lim_{\eta_x \to x_0}\dfrac{f'(\eta_x)}{g'(\eta_x)} $ nên không thể kết luận được

$\lim_{x \to x_0} \dfrac{f(x)-f(x_0)}{g(x)-g(x_0)}=\lim_{x \to x_0} \dfrac{f'(x)}{g'(x)} $

Cho $L_1=2, L_2=1$ và $L_{n+2}=L_{n+1}+L_n$ với $n\ge 1$ thỏa mãn dãy Lucas. Chứng minh rằng $\prod \limits_{k=1}^m L_{2^k+1}=F_{2^m+1}$ với $\{F_n\}_n$ là dãy Fibonacci.

Cần chú ý vấn đề này nha Kiên. Mặc dù dãy Fibonaci ai cũng biết , tuy nhiên, có thể định nghĩa nó bắt đầu từ $F_0$ hoặc $F_1$ hoặc bắt đầu từ $F_k$ nào đó chẳng hạn..về bản chất thì cách định nghĩa đó không ảnh hưởng gì....nhưng...nếu thay vào một công thức nào đó thì phải định nghĩa chính xác, số bắt đầu dãy Fibonaci lấy từ chỉ số nào.

Đề bài trên sai rồi nhé, chắc do đánh máy nhầm.

Dãy Fibonaci định nghĩa bởi

$\begin{cases} F_1=F_2=1 \\ F_{n+2}=F_{n+1}+F_n \; \forall n \ge 1 \end{cases} $

Khi đó, ta có đẳng thức $\prod_{k=1}^m L_{2^k+1}=F_{2^{m+1}} \;\; , m \in \mathbb{N}^* $


P/s: Thường dãy Lucas định nghĩa từ chỉ số 0, tức $L_0=2;\;L_1=1 \;;, L_{n+2}=L_{n+1}+L_n \;\; \forall n \in \mathbb{N}^*$

Nguyên nhân định nghĩa từ chỉ số 0 là để các công thức liên hệ với dãy Fibonaci được đẹp đẽ hơn.

Cụ thể

$L_n=F_{k+2}L_{n-k}+F_{k+1}L_{n-k-1} \; , \forall k<n $

$F_{2n}=L_nF_n$

$L_n^2=5F_n^2+4(-1)^n$

...
_____
Em dịch từ tiếng anh qua Tiếng Việt nên chả biết đúng không

Lý thuyết nè mấy bạn.


Họ $\mathbb{A}$ các tập con của $X \ne \emptyset $ được gọi là một đại số các tập con của $X$ nếu

a) $X \in \mathbb{A}$

b) $A \in \mathbb{A} \Rightarrow {C_X}A = X\backslash A \in \mathbb{A}$

c) ${A_i} \in \mathbb{A} \Rightarrow \bigcup\limits_{i = 1}^n {{A_i}} \in \mathbb{A}$

$ \bullet {\text{ }}\emptyset \in \mathbb{A} \Rightarrow X\backslash \emptyset \in \mathbb{A} \Rightarrow X \in \mathbb{A}$

$ \bullet {\text{ }}A \in \mathbb{A} \Rightarrow X\backslash A \in \mathbb{A}{\text{ }}\left( {{\text{gt}}} \right)$

Ý thứ 3 chứng minh như thế nào mấy bạn???

Ý thứ 3:

$A_i \in \mathbb{A} \Rightarrow C_XA_i \in \mathbb{A} $

$\Rightarrow \bigcap_{i=1}^n C_XA_i \in \mathbb{A} $

$\Leftrightarrow C_X (\bigcup_{i=1}^n A_i) \in \mathbb{A} $

$\Rightarrow C_X(C_X (\bigcup_{i=1}^n A_i)) \in \mathbb{A} $

$\Leftrightarrow \bigcup_{i=1}^n A_i \in \mathbb{A}$

Chủ yếu là vận dụng linh hoạt các luật De Morgan !

Dãy Perrin là dãy được xác định bởi $P_0=3;P_1=2;P_2=2;P_n=P_{n-2}+P_{n-3}$. Chứng minh rằng nếu $n$ là số nguyên tố thì $n|P_n$

Sai rồi Kiên !

Dãy Perrin

$$\begin{cases}P_0=3 \;, P_1=0 \;, P_2=2 \\ P_n=P_{n-2}+P_{n-3} \;\;,\forall n \ge 3 \end{cases} $$

Khi đó, với $n$ nguyên tố thì $n | P_n $


Dãy của em trên kia, cho $n=3$ thấy ngay $P_3=5 $ vậy đâu có $3 |P_3$

Một số tính chất khác của dãy Perrin

Với $p$ nguyên tố thì, $P_{pn} \equiv P_n \; (mod p) \; \forall n \in \mathbb{N}$

Nếu mở rộng dãy sang cả tập số nguyên bằng cách sử dụng : $P_{n-3}=P_n-P_{n-2} $

Với 3 số nguyên $m;n;k$ bất kỳ luôn có : $P_{mn+k}=P_mP_{m(n-1)+k}-P_{-m}P_{m(n-2)+k}+P_{m(n-3)+k} $

$P_{2n}=P_n^2-2P_{-n} $

$P_{3n}=P_n^3-3P_nP_{-n}+3$

$P_{2n+1}=P_nP_{n+1}+P_{1-n}$

Với ma trận vuông cấp 3

$A= \begin{bmatrix} a_{11} &a_{12} &a_{13} \\ a_{21}&a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{bmatrix}$$A= \begin{bmatrix} a_{11} &a_{12} &a_{13} \\ a_{21}&a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{bmatrix}$

Thì định thức con chính có tới 3 cái:

Định thức con chính cấp 1: $|a_{11}|$

Định thức con chính cấp 2: $\begin{vmatrix} a_{11} &a_{12} \\ a_{21}&a_{22} \end{vmatrix}$

Định thức con chính cấp 3: $ \begin{vmatrix} a_{11} &a_{12} &a_{13} \\ a_{21}&a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{vmatrix}$


Định thức con chính cấp $k$ của ma trận vuông $A$ cấp $n$ là định thức của ma trận khối tạo thành từ $k$ dòng và $k$ cột đầu tiên của $A$

Các bạn giải giúp mình bài này bằng VCB với
$ \lim_{x\to 0}\frac{x-sin5x+sin^2x}{4x+arcsin^2x+x^2} $

Thật ra cũng chẳng cần VCB làm gì, nhưng nếu VCB thì:

$\lim_{x\to 0}\frac{x-sin5x+sin^2x}{4x+arcsin^2x+x^2}=\lim_{x \to 0} \dfrac{1-\frac{\sin 5x}{x}+\frac{\sin^2x}{x}}{4+\frac{\arcsin^2x}{x}+x}$

Ta biết rằng

$\frac{\sin x}{x} \underset{x \to 0}\sim 1 $

$\frac{\arcsin x}{x} \underset{ x \to 0} \sim 1$

$\Rightarrow \dfrac{1-\frac{\sin 5x}{x}+\frac{\sin^2x}{x}}{4+\frac{\arcsin^2x}{x}+x} \underset{x \to 0} \sim \dfrac{1-5+\sin x}{4+\arcsin x}\underset{x \to 0}\sim -1 $

$\Rightarrow \lim_{x\to 0}\frac{x-sin5x+sin^2x}{4x+arcsin^2x+x^2}=-1 $

Nếu như em nhớ không lầm thì có 1 nhà toán học đã chứng minh $\pi, \epsilon$ các số siêu việt, tức là các số không thể biểu diễn được dưới dạng căn thức. Thì do đó, không thể có quy luật được. Vì nếu có quy luật thì $\pi,\epsilon$ lại trở thành một số hữu tỷ????

Mình đã tìm ra quy luật số PI, khảo sát với 99 số thập phân của số PI, viết trong file đính kèm.
Mong nhận được góp ý các bạn !

Liên hệ:
Gmail: [email protected]
Yahoo: [email protected]
DĐ: 01662 615 061

Số Pi và cả số e đều biểu diễn được dưới dạng liên phân số mà quy luật đã biết rõ:

$e=[2;1;2;1;1;4;1;1;6;1;1;8;1;1;10;1...;1;2n;1...] $

tức

$e=2+\dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{4+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{6+\dfrac{1}{1+...}}}}}}}}}$

Số Pi biểu diễn dạng liên phân số chính tắc thì không có quy luật, nhưng có thể biểu diễn dạng liên phân số theo cách khác nhưng có quy luật rất đẹp, chẳng hạn:


$\pi=\dfrac{4}{1+\dfrac{1}{2+\dfrac{3^2}{2+\dfrac{5^2}{2+\dfrac{7^2}{2+\dfrac{9^2}{2+...}}}}}}$


$=3+\dfrac{1}{6+\dfrac{3^2}{6+\dfrac{5^2}{6+\dfrac{7^2}{6+\dfrac{9^2}{6+...}}}}}$

$=\dfrac{4}{1+\dfrac{1}{3+\dfrac{2^2}{5+\dfrac{3^2}{7+\dfrac{4^2}{9+...}}}}}$


Hy vọng sẽ giúp ích cho nghiên cứu phép suy !

Như ta đã biết, số e là một số vô tỉ và phép chứng minh cũng không mấy khó khăn. Mạnh hơn nữa, e là một số siêu việt, tức nó không là nghiệm của phương trình đại số nào.

Tập các số siêu việt là không đếm được nhưng tập số đại số ( là nghiệm của một phương trình đại số) là đếm được, từ đó, có thể hình dung rằng, tập hợp các số siêu việt là "nhiều hơn" tập số đại số! Tuy nhiên, chứng minh một số là số siêu việt lại là điều rất khó. Hai số siêu việt quan trọng nhất là $\pi $ và $e$ . Hiện nay cũng có nhiều cách chứng minh, nhưng hôm nay xin trình bày một cách chứng minh $e$ là số siêu việt, cách chứng minh này cũng có thể cải biên tí để chứng minh cho trường hợp số $\pi$, mà tôi thấy dễ hiểu.

Chứng minh:

Với mọi số thực x và đa thức $P \in \mathbb{R}[x]$ , xét $I_P(x)=\int_0^x e^{x-t}P(t)dt $

$I_P(x)=[-e^{x-t}P(t)]|_0^x+\int_0^x e^{x-t}P'(t)dt=(e^xP(0)-P(x))+I_{P'}(x) $

$=...=e^x\sum_{i=0}^{deg (P)} P^{(i)}(0)-\sum_{i=0}^{deg(P)} P^{(i)}(x) $

Ký hiệu $Q_P$ là đa thức thu được khi thay trong $P$ mỗi hệ số bằng giá trị tuyệt đối của nó.

** Với $x \ge 0$ :

$|I_P(x)| \le \int_0^x e^{x-t} Q_P(|t|)dt \le \int_0^x e^{x-t} Q_P(|x|)dt \le xe^xQ_P(|x|) $

** Với $x \le 0$

$|I_P(x) =\begin{vmatrix} \int_0^x e^{x-t}P(t)dt\end{vmatrix} \le \int_x^0 e^{x-t} Q_P(|t|)dt \le (-x)Q_P(|x|) \le (-x)e^{-x}Q_P(|x|) $

Vậy $${\color{Blue} { \forall x \in \mathbb{R} \;\;, |I_P(x)| \le |x|e^{|x|}Q_P(|x|) }}$$

Giả sử rằng $e$ là số đại số, tức tồn tại ${\color{Blue}{ n \in \mathbb{N}^* }}$ và ${\color{Blue}{(a_0;...;a_n) \in \mathbb{Z}^{n+1}}}$ sao cho

${\color{Blue}{a_0 \neq 0 }}$ và ${\color{Blue}{ \sum_{i=0}^n a_i e^i =0 }}$

Xét số nguyên tố $p$ ( xác định sau ) và đa thức

${\color{Red}{P=x^{p-1} \prod_{k=1}^n (x-k)^p }}$ với ${\color{Blue}{deg(P)=pn+p-1 }}$

${\color{Red}{E=\sum_{k=0}^na_k I_P(k) }}$


Ta có: ${\color{Blue}{E}}=\sum_{k=0}^na_k (e^k \sum_{i=0}^{deg(P)} P^{(i)}(0)-\sum_{i=0}^{deg(P)}P^{(i)}(0) )$

$=\sum_{k=0}^n a_ke^k \sum_{i=0}^{deg(P)} P^{(i)}(0) -\sum_{i=0}^{deg(P)} \sum_{k=0}^n a_kP^{(i)}(0) $

$={\color{Blue}{-\sum_{i=0}^{deg(P)} \sum_{k=0}^n a_k P^{(i)}(k) }}$

Xét $(i,k) \in \{0;...;deg(P)\} \times \{0;...;n\} $


** Với $i \le p-1 $ và $ k\ge 1 $

Khi đó, $(x-k)^{p-i} $ chia hết $P^{(i)} $ nên $P^{(i)}(k)=0 $

** Với $i \ge p$ và $k \ge 1 $

$P$ có dạng : $P=R(x-k)^p $ , trong đó $ A \in \mathbb{Z}[x] $

Theo công thức Leibniz cho đạo hàm của một tích hai hàm số:

$P^{(i)}=\sum_{j=0}^i C_i^jR^{(i-j)} ((x-k)^p)^{(j)} $

$ \Rightarrow P^{(i)}(k)=C_i^p R^{(i-p)}(k) p! $ , do đó , $p! $ chia hết $P^{(i)}(k) $


** Với $i \le p-2 $ và $k=0$

Khi đó, $x^{p-1-i} $ chia hết $P^{(i)} $ nên $P^{(i)}(k) $=0

** Với $ i \ge p$ và $ k=0$

$P$ có dạng $P=H^p x^{p-1} $ , trong đó $H \in \mathbb{Z}[x] $

Cũng theo công thức Leibniz :

$P^{(i)}=\sum_{j=0}^i C_i^j (H^p)^{(i-j)} (x^{p-1})^{(i)} $

$\Rightarrow P^{(i)}(0)=C_i^{p-1}(H^p)^{(i-p+1)}(0) (p-1)! =C_i^{p-1} (H^{p-1}H')^{(i-p)}(0) p ! $

do đó $p!$ chia hết $P^{(i)}(k)$ .

** Với $i=p-1 $ và $k=0\;\;, n<p$

Tương tự trường hợp $ i \ge p $ và $k=0$ ở trên, $P$ cũng có dạng $P=H^p x^{p-1} $ , $\;\; H(x)=\prod_{k=1}^n (x-k) $, thế thì

$P^{(p-1)}(0)=C_{p-1}^{p-1} H^p(0)(p-1)=((-1)^n n! )^p (p-1)!!$

Vì $1 \le n<p $ và $p$ là số nguyên tố nên $p$ không chia hết $(-1)^n n! $ , vậy nên $(p-1)! $ chia hết $P^{(p-1)}(0) $ và $p!$ không chia hết $P^{(p-1)}(0) $ .


Vậy ta vừa chứng minh rằng:

$${\color{Blue}{\left\{\begin{matrix} p! \;\;\;\;\;\text{chia het}\; P^{(i)}(k)\; \text{neu}\; (i,k) \neq (p-1,0)\\(p-1)!\;\;\;\text{chia het}\;P^{(p-1)}(0)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;. \\ p!\;\;\;\;\;\text{khong chia het}\;P^{(p-1)}(0) \;\text{neu}\; p>n \end{matrix}\right.}}$$



Xét $p>n$ và $p >|a_0|$

Áp dụng cho đa thức $E$ kết quả mới thu được ở trên ta có :

$p! $ chia hết mọi số hạng dạng $a_kP^{(i)}(k) \; \;, k \ge 1 $ .

$(p-1)! $ chia hết $a_0P^{(p-1)}(0)$ nhưng $p!$ không chia hết $a_0P^{(p-1)}(0)$

Vậy $(p-1)! $ chia hết $E$ và $p!$ không chia hết $E$

Suy ra $E$ là một bội khác không của $(p-1)!$ , do đó ${\color{Red}{|E| \ge (p-1)! }}$


Với $P=x^{p-1} \prod_{i=1}^n (x-i)^p $ thì $Q_P=x^{p-1} \prod_{i=1}^n (x+i)^p $

$\Rightarrow Q_P(k)=k^{p-1} \prod_{i=1}^n (k=i)^p \le (2n)^{p-1+np}=(2n)^{deg(P)} $

Vậy $\forall k \in \{0;...;n\} \;\;, |I_P(k)| \le ke^kQ_P(k) \le ne^n (2n)^{deg(P)} $

$\Rightarrow {\color{Blue}{|E|}} \le \sum_{k=0}^n |a_k||I_P(k)| \le (\sum_{k=0}^n |a_k|) ne^n(2n)^{deg(P)} \le (\sum_{k=0}^n |a_k|) ne^n(2n)^{(n+1)p}{\color{Blue}{ \le C^p}}$

trong đó $C=(\sum_{k=0}^n |a_k|) ne^n(2n)^{n+1}$


Tóm lại, ta vừa chứng minh rằng, tồn tại số nguyên $N = \max(n,|a_0|) $ và một số $C \in \mathbb{R}_+^* $ sao cho với mọi số nguyên tố p thỏa mãn $ p>N$ thì ta có: $(p-1)! \le |E| \le C^p $ hay ${\color{Blue}{\dfrac{C^p}{(p-1)!} \ge 1 }}$

Do tập các số nguyên tố là vô hạn, chuyển qua giới hạn khi $p \longrightarrow +\infty$ , ta được $ {\color{Blue}{\dfrac{C^p}{(p-1)!} \longrightarrow 0}}$ do tính trội của giai thừa so với hàm mũ.

Vậy ta nhận được sự mâu thuẫn, do đó $e$ không là số đại số, tức

$e$ là số siêu việt .


P/s: Tham khảo từ Alan Baker, Transcendantal number theory , ĐH Cambdridge. Một tài liệu rất hay và rất khó về số học. Hic, cũng may mình không đam mê và rất dốt số học.

Một số cách chứng minh khác (cho cả số $\pi$) có thể tìm thấy ở các tài liệu kèm theo bên dưới.

xin hỏi ý kiến của các vị: $\begin{cases} & \text{} a=x+y+z \\ & \text{} b=xy+xz+yz \\ & \text{} c=xyz \end{cases}$ thì khi đó $s_{k}=x^{k}+y^{k}+z^{k}$ được biểu diễn qua a,b ,c như thế nào

Thật ra biểu diễn $S_k$ theo các đa thức đối xứng sơ cấp đã hoàn thiễn rất lâu rồi. Thời PT tôi đã thấy nó trong một quyển sách thầy giáo cho tôi mươn, tiếc rằng quên biểu diễn thế nàp rồi. Người ta thâm chí còn lập một sơ đồ hệ số nữa, nó tựa như tam giác Pascal vậy. Hình như tuyển tập 35 năm toán học tuổi trẻ thì phải.

haisupham nên vào thư viện trường tìm các cuốn lịch sử Toán học mà đọc, để biết những gì ta học hôm nay, nhân loại hàng ngàn năm TCN đã tìm ra cả rồi...chỉ có điều còn sót lại một phần rất rất ít những kiến thức đó cho tới ngày nay. Đọc đi rồi bạn sẽ rất ngạc nhiên cho mà xem, và đó cũng là một cách tốt để bạn mở rộng miệng giếng cho to hơn.

mình mới mua một laptop dell ínpiron, không biết nghịch thế nào nhấn F12, rồi sau một vài thao tác nữa thì nó hiện lên một màn hình đen ghi "internal hard disk drive not found, to reslve this issue, try to reseat the drive. no bootable devices--strike F1 to retry boot, F2 enter Setup Menu, F5 enter PSA".
mình đã nhấn F5 để test rồi cũng không đuợc, nhấn F2 để cài cũng không được, nhấn F1 thì nó vẫn ra như thế, chẳng biết phải làm sao cả, bạn nào biết cách xử lí thì bày giúp mình!

Hình như bạn vọc trong BIOS đúng không? Nếu thế thì gần như chắc chắn bạn đã vọc phần cấu hình AHCI cho ổ cứng. Rất có thể ổ cứng bạn không hỗ trợ SATA nhưng bạn đã cấu hình AHCI về SATA nên hiển nhiên máy không thể nhận ra ổ cứng để khởi động, các dòng laptop khác như máy của mình thì khởi động đến màn hình logo windows thì lỗi màn hình xanh. Bạn cấu hình lại AHCI về IDE là được, sau đó lưu thiết lập và khởi động lại. Chúc thành công.

Với $a_{1}+a_{2}=1$ và $x_{1}, x_{2},a_{1}, a_{2}> 0$
Chứng minh:
$a_{1}x_{1}+a_{2}x_{2}\geq x_{1}^{a_{1}}x_{2}^{a_{2}}$

Bài này chắc có lẽ có rất nhiều cách giải, chẳng hạn dùng bdt $e^x \ge 1+x \; \forall x \ge 0 $

Tại dân giải tích suy nghĩ gì nó cũng dính giới hạn nên ra nông nổi này đây.

Trước tiên, xét $a;b$ là số hữu tỉ.

Đặt $a=\dfrac{m}{n} \;, b=\dfrac{p}{q} \;\; m,n,p,q \in \mathbb{N}^* $

$\Rightarrow \dfrac{m}{n}+\dfrac{p}{q}=1 \Leftrightarrow mq+np=pq $

Ta cần cm : $ \dfrac{m}{n}x_1+\dfrac{p}{q}x_2 \ge x_1^{\frac{m}{n}}x_2^{\frac{p}{q}}$

$\Leftrightarrow mqx_1+npx_2 \ge nq x_1^{\frac{m}{n}}x_2^{\frac{p}{q} }$

Áp dụng bdt AM-GM cho $mq$ số $x_1$ và $np$ số $x_2$ là có ngay đpcm.

Bây giờ, mở rộng ra số thực.

Với mỗi số thực $a\;, b \in \mathbb{R}_+^* \;\;, a+b=1$ , tồn tại 4 dãy số nguyên dương $m_t,n_t,p_t,q_t \; \dfrac{m_t}{n_t}+\dfrac{p_t}{q_t}=1$ sao cho

$a=\lim_{t \to +\infty} \dfrac{m_t}{n_t} $

$b=\lim_{t \to +\infty} \dfrac{p_t}{q_t} $

Do $ \dfrac{m_t}{n_t}x_1+\dfrac{p_t}{q_t}x_2 \ge x_1^{\frac{m_t}{n_t}}x_2^{\frac{p_t}{q_t}}\;\;, \forall t \in \mathbb{N}^*$

sử dụng tính liên tục của hàm mũ, cho $t \longrightarrow +\infty$ , ta thu được

$ax_1+bx_2 \ge x_1^ax_2^b $

Mở rộng bdt cho $n$ số ta được AM-GM suy rộng.

Với $2n$ số thực dương $a_1;...a_n;x_1;...;x_n$ sao cho $ x_1+x_2+...+x_n=1$

Ta luôn có: $x_1a_1+x_2a_2+...+x_na_n \ge a_1^{x_1}a_2^{x_2}...a_n^{x_n} $

Cho $n$ số bất kỳ (kể cả phức) $x_i \;, i \in \{1;...;n\}$

Đa thức đối xứng sơ cấp thứ $k$ của $n$ số $x_i$ (elementary symmetric polynomials), ký hiệu $E_k(x_1,...,x_n)=\sum_{1\le i_1<...<i_k\le n}x_{i_1}...x_{i_k} $

Tổng lũy thừa bậc $k$ của $n$ số $x_i$ : $S_k(x_1,...,x_n)=x_1^k+x_2^k+...+x_n^k $

Theo định lý Viète , $n$ số $x_i$ là nghiệm của phương trình :

$X^n+a_1X^{n-1}+...+a_{n-1}X+a_n=0 $ , trong đó $a_i=(-1)^i E_i(x_1,...,x_n) \;\;, i \in \{1,...,n\} $

Công thức Newton (Newton's formula) :

$$\boxed{ \begin{matrix} \forall k \in \{1,...,n\} ,\;\; S_k+a_1S_{k-1}+...+a_{k-1}S_1+ka_k=0 \\ \\ \forall p>n ,\;\; S_p+a_1S_{p-1}+...+a_nS_{p-n}=0\end{matrix} }$$

Nếu viết dưới dạng đa thức đối xứng sơ cấp thì ta có:

$\sum_{i=0}^{k-1} (-1)^iE_iS_{k-i}+(-1)^kkE_k=0=\sum_{i=1}^{k} (-1)^iE_{k-i}S_i+kE_k=0 \;\; \forall 1 \le k \le n $

(Đây cũng chính là công thức đã được chứng minh ở đây .)

$\sum_{i=0}^n (-1)^iE_iS_{p-i}=\sum_{p-n}^p (-1)^{p-i}E_{p-i}S_i=0 $


Ta có một cách chứng minh rất hay bằng công cụ giải tích sau đây ( trích trong một file đính kèm bên dưới) :

Để tổng quát, ta định nghĩa tổng lũy thừa bậc $k$ của $n$ biến $x_i \;\;, i \in \{1,...,n\} $ mở rộng :

$$s_{k}(x_1,...,x_n) \begin{cases} x_1^k+x_2^k+...+x_n^k \;\;\;, k>0 \\ n \;\;\;\;, k=0\\ 0 \;\;\;\;,k<0 \end{cases} $$

Đa thức sơ cấp thứ $k$ mở rộng

$$e_k(x_1,...,x_n)= \begin{cases} \sum_{1 \le i_1<...<i_k\le k} x_{i_1}...x_{i_k} \;\;\;, 1 \le k \le n \\ 1 \;\;\; , k=0 \\ 0 \;\;\;, k<0 \vee k>n \end{cases} $$


Xét $f(x)=\prod_{i=1}^n (x-x_i)=\sum_{i=0}^n(-1)^ie_ix^{n-i}=\sum_{i \in \mathbb{Z}} (-1)^ie_ix^{n-i}$

$f'(x)=\sum_{i \in \mathbb{Z}} (-1)^i(n-i)e^ix^{n-i-1}$

$\Rightarrow \dfrac{f'(x)}{f(x)}=\sum_{i=1}^n\dfrac{1}{x-x_i} $

Lại có : $\dfrac{1}{x-r}=\sum_{j=0}^{\infty} \dfrac{r^j}{x^{j+1}}$

Cho nên :$ f'(x)=f(x) \dfrac{f'(x)}{f(x)}=f(x) \sum_{i=1}^n \sum_{j=0}^{\infty} \dfrac{x_i^j}{x^{j+1}}$

$=g(x)\sum_{j=0}^{\infty}\sum_{i=1}^n \dfrac{x_i^j}{x^{j+1}}=g(x)\sum_{j \in \mathbb{Z}} \dfrac{s_j}{x^{j+1}}$


$=\sum_{i,j \in \mathbb{Z}} (-1)^i e_i s_jx^{n-i-j-1} $

$=\sum_{j \in \mathbb{Z}} ( \sum_{i \in \mathbb{Z}} (-1)^ie_is_{j-i}) x^{n-j-1} $ ( thay $j$ bởi $i+j$ )


So sánh hệ số của $f'(x)$ được tính bằng 2 cách cho ta đẳng thức :

$\sum_{i=0}^{j-1} (-1)^ie_is_{j-i}+(-1)^je_jn=(-1)^je_j(n-j) $

$\Leftrightarrow \sum_{i=0}^{j-1}(-1)^ie_is_{j-i}+(-1)^jje_j=0$

$\Leftrightarrow \sum_{i=1}^k (-1)^ie_{k-i}s_i +ke_k=0 $ ( thay $i$ bởi $j-i$ , thay $j$ bởi $k$, sau đó chia cho $(-1)^k$ )


Công thức Newton ở trên rất mạnh trong việc tạo ra các đẳng thức đẹp, từ đó có thể sáng tạo ra bất đẳng thức, giải hệ phương trình, giải phương trình bậc cao...

Một vài bài tập khá hay xin trích trong một số tài liệu kèm bên dưới:

1) Cho $P_n=a^n \sin(nA)+b^n \sin(nB)+c^n \sin(nC) \;\;\;, (a,b,c,A,B,C) \in \mathbb{R}^6$ , $A+B+C$ là bội của $\pi$

Giả sử $P_1=P_2=0$ , chứng minh $P_n=0 \;\;,\forall n \in \mathbb{N} $

2) Tìm $a$ sao cho tất cả nghiệm của phương trình sau đều là số thực:

$ x^6+3x^5+(6-a)x^4+(7-2a)x^3+(6-a)x^2+3x+1=0 $

3) Biết rằng các nghiệm của phương trình sau tạo thành một cấp số cộng (đều là nghiệm thực)

$x^5-5x^4-35x^3+mx^2+nx+p=0$ với $m,n,p$ là các hằng số thực.

Tìm các nghiệm đó.


P/s: Càng đọc sách nước ngoài thì càng thấy mình ngu ra và cảm giác học Toán ở Việt Nam còn quá tụt hậu ! Hic, cố gắng đọc nhiều tài liệu nước ngoài để mở rộng hiểu biết , ít ra cũng tránh bị rơi xuống giếng !

1) Đây không phải ma trận phảm đối xứng. Vì ma trận phản đối xứng thì các phần tử trên đường chéo chính phải bằng 0.

2) Có lẻ đề thiếu điều kiện $a\neq 1$

3) Giải với điều kiện $a\neq 1$

Ta đặt $A=\begin{pmatrix} a+1 & b & c & d\\ -b & a+1 & b & c\\ -c & -b & a+1 & b\\ -d & -c & -b & a+1 \end{pmatrix}$

Ta có:

$AA^{T}=\left [ (a+1)^{2}+b^{2}+c^{2}+d^{2} \right ].I$

$\Rightarrow \det (AA^{T})=\left [ (a+1)^{2}+b^{2}+c^{2}+d^{2} \right ]^{4}$

$\Rightarrow (\det A)^{2}=\left [ (a+1)^{2}+b^{2}+c^{2}+d^{2} \right ]^{4}$

Với $a\neq 1$ thì $\det A\neq 0$

Suy ra ma trận A khả nghịch

Như đã tính $\det(A)=[(a+1)^2+b^2+c^2+d^2]^2 $ , do đó, để $A$ khả nghịch thì phải có $(a+1)bcd \neq 0$ . Điều kiện $a \neq 1$ không thể đảm bảo $A$ khả nghịch!

em à.chúng ta cần phải làm cho anh rõ, anh vẩn chưa xác định được công thức lop chuẩn dưới tồn tại trong 5 tài liệu em đã post lên diễn đàn, bây giờ để giúp chúng ta rõ ràng, em hãy chụp lại cái vị trí trong 5 tài liệu đó vào đăng lên, anh sẽ giải thích tại sao nó không phải là công thức lop chuẩn dưới.

làm phiền em một chúc. công thức trong đó không phải là công thức lop chuẩn dưới. anh đã tìm trong 5 tài liệu . có giống vài công thức nhưng nó không phải là công thức lop chuẩn dưới, nên phiền em giúp anh làm sáng tỏ

trong công thức lop chuẩn dưói nó tồn tại 2 biến n và k. hãy chỉ rõ vị trí nằm trên tài liệu . bằng cách chụp hình lại và post lên, nằm ở trang mấy của tài liệu trên

nếu từ công thức lop chuẩn dưới . ta lấy n=k thì nó thành công thức lop chuẩn, nên anh chỉ nhìn thấy công thức lop chuẩn trong tài liệu chứ không tìm thấy công thức lop chuẩn dưới., vì công thức lop chuẩn có có hình dạng giống công thức lop chuẩn dưới, nhưng chỉ được 1 biến n mà thôi.

vì khả năng áp dụng công thức lop chuẩn dưới rất mạnh, nên anh nghĩ không có lý do nào nó tồn tại mà ít ứng dụng, và không được trường đại học chú ý

Em có viết rành rành trong bài viết trên rồi, phần đóng khung to đùng!

Một phần quan trọng, $lop(m,1,n)=E_{m,n}$ , tất cả công thức của $lop$ hiện giờ chỉ có ở $lop(m,1,n)$ , mà như đã có ở trên, công thức Newton ! Với $lop(m,k,n)$ thì anh có thể xem về Schubet Polinomials

Ứng dụng của công thức Newton rất nhiều, trong file đính kèm có một số đề USAMO, những vấn đề liên quan hầu như đã hoàn thiện. Do đó, cũng không lý do gì mà ĐH lại đi nghiên cứu cái mà tiền nhân đã làm rồi, hơn nữa, ĐH VN thì anh biết, nghiên cứu rất ít, hầu hết đi sau nhân loại cả chặng đường dài, những gì mình có thì Tây, Tàu nó có cả rồi ! Sách tiếng Việt cũng có đề cập tới công thức Newton, cái này em không nhớ nó tên gì, nhưng chắc chắn có ! Có thể anh chưa được tiếp cận với nền Toán học đã quá phát triển của thế giới nên còn nhiều thứ chưa biết !

Về phần dãy lop thì đó hoàn toàn của anh, ít ra là tên gọi! Tuy nhiên, bản chất nó là biểu diễn hình thức cho các đối xứng sơ cấp, hình thức mà không ruột thì rỗng toét ạ.

Phần giải đáp thắc mắc đã xong, chắc em không cần chụp hình, anh chịu khó xem lại ạ !

trời ơi, anh đã tìm trong 5 tài liệu đó rồi ,không có cái nào như cái đóng khung của em viết ở trên hết, đã tìm hết rồi là không có.trường đại học nó có cho anh học về vấn đề này,nhưng không bao giờ có sử dụng công thức như vậy

Trong introductions to symmetric polynomials and symmetric function trang 16 (file này anh đọc kỹ, khá đầy đủ về đa thức đối xứng sơ cấp, anh sẽ bắt gặp lop trong đó chẳng hạn Example 3.2)

trong tài liệu chỉ tìm thấy chỗ khoanh tròn màu đen tương đương với công thức lop chuẩn .còn công thức lop chuẩn dưới chưa tìm thấy:

À, anh xem kỹ, nó ghi là

$S_1+c_1=0$

$S_2+c_1S_2+2c_2=0$

$S_3+c_1S_2+c_2S_1+3c_3=0$
....

$S_n+c_1S_{n-1}+...+c_{n-1}S_1+nc_n=0 $

Phần ... chính là nó lược bỏ $S_k+c_1S_{k-1}+...+c_{k-1}S_1+kc_k=0 $ đó ạ, nó có liệt kê 3 tổng đầu rồi. Hơn nữa, anh tìm trong introductions to symmetric polynomials and symmetric function trang 16 có đủ, hay symmetric polinomials trang 6.

Bài viết của em, em viết theo lối em hiểu và đã thu gọn lại cho tổng quát nên tất nhiên nó không giống 100% như trong các tài liệu.

Rồi, mọi chuyện đã sáng tỏ, anh thành thật cảm ơn em nhiều, và rất nhiều, anh đã thoã mãn mọi điều,
nhưng vẩn còn cái thằng phương trình bậc 4 vẩn chưa tìm thấy, vẫn chưa thoả mãn, lúc trước nesbit có nói tìm giúp, mà cuối cùng đi đâu mất rồi,

Anh vẩn còn hy vọng cuối cùng trong phép biện luận nghiệm phương trình bậc 4, anh mong còn có 1 cái không trùng khớp, tất nhiện phương trình bậc 4 được người ta giải nhưng cách phân tích của anh là độc quyền, điều hy vọng thêm 1 điều nưa là anh sẽ cố gắng tìm lại 1 con số trong số học, số đó được anh tìm ra giống sô PI vậy ,nhưng có ứng dụng . anh đã quên rồi, mong rằng có 2 điều không bị trùng khớp

Em cũng cảm ơn anh rất nhiều vì sự sáng tạo đó cũng đáng cho em học hỏi và xin tuyên dương tinh thần sáng tạo của anh ạ. Về phần phương trình bậc 4, để em thử tìm xem, vấn đề là search google bằng từ khóa gì, search tiếng Việt thì không ra, tiếng anh thì không biết dùng từ gì cho đúng nữa @@. Mong rằng còn số tựa như Pi sẽ sớm được công bố. Chúc anh thành công !