sr các bạn mình gõ nhầm đề. Hì

Cho đa thức:

$f(x)= a_{2004}x^{2004}+ a_{2003}x^{2003}+...+ a_{1}x + a_{0} $ thoả mãn $ f(1)= -1, f(2003)= 4$.

Chứng minh tồn tại cấp số cộng $\div a,b,c,   a<b<c$   thoả mãn   $f(a)+f(b)+f(c) = 0$.

Chứng minh rằng trọng mọi $\Delta ABC$ ta đều có:

 

$\sqrt{3}\leq  \frac{\cos\frac{A}{2}}{1+\sin\frac{A}{2}} + \frac{\cos\frac{B}{2}}{1+ \sin\frac{B}{2}} +\frac{\cos\frac{C}{2}}{1+\sin\frac{C}{2}} <2$

có ai làm được câu III phần 2 chưa vậy?

Cho $\Delta ABC$. Chứng minh rằng:
$\sqrt{3} < \cos{\frac {A}{2}(1+ sin {\frac{A}{2}})} + \cos{\frac {B}{2}(1+ sin {\frac{B}{2}})} + \cos{\frac {C}{2}(1+ sin {\frac{C}{2}})} < 2$

Đúng ùi nk k còn cách nào ngoài đạo hàm ạ?

Cho hàm số $y=\sqrt{2\sin x-1}+\sqrt{2\cos x-1}$.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Tìm giới hạn:
$L=\lim_{x\to+\infty}x^2\left(\sqrt{\frac{x+2}{x}} - \sqrt[3]{\frac{x+3}{x}}\right)$.

Cho hàm số $y=\sqrt{2\sin x-1}+\sqrt{2\sin x+1}$.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Chuẩn hoá x+y+z=1
Ta có $(y+x+z)(y+z+z)\ge(y+\sqrt{zx}+z)^2$hay $(y+\sqrt{zx}+z)^2\le y+2z$ nên ta cần cm
$\sum{\frac{2x^2+xy}{2z+y}}\ge 1$
lại có $\sum{\frac{2x^2+xy}{2z+y}} = \sum{\frac{x(2x+y)^2}{(2z+y)(2x+y)}} \ge \sum{\frac{x(2x+y)^2}{(x+y+z)^2}}=\sum{\frac{(2x^2+xy)^2}{x}}\ge\frac{(2x^2+2y^2+2z^2+xy+yz+zx)^2}{x+y+z}\ge1$

Đoạn cuối trc chỗ >=1 sao ra đc như tek vậy bạn

$\sum_{cyc}\frac{2x^{2}+xy}{(y+\sqrt{zx}+z)^{2}}=\sum_{cyc}(\frac{x^{2}+xy}{(y+\sqrt{zx}+z)^{2}} + \frac{z^2}{(x+\sqrt{yz}+y)^{2}})\geq\sum_{cyc}\frac{(x+\sqrt{xy}+z)^2}{(y+\sqrt{zx}+z)^{2}+(x+\sqrt{yz}+y)^{2}}\geq 1$

Bạn giải thích hộ mình cái đoạn cuối với, chỗ tổng hoán vị cuối cùng í, sao lại ra như tek, dùng bđt phụ j vậy

dễ mà.em đọc trước phần đó 1 chút là hiểu.hồi anh học phổ thông thì đạo hàm với tích phân học từ lớp 10.Em ở đâu bắc giang.anh yên dũng nè

lạng giang ạ. tks a để e xem thử. hì

chắc là có nhưng a không nghĩ ra,em học lớp 10 à,đọc qua định nghĩa của đạo hàm là em hiểu ngay ấy mà.đằng nào chả phải học

Anh cũng bắc giang này
em thử dồn biến ra biên xem.a chưa thử nhưng chắc là được.ngại nháp

E lớp 11 nk chưa học đến đạo hàm, mới biết tí tìm đạo hàm đơn giản thôi chứ định lí các thứ chưa đc học ạ

sr mod em không biết gõ latex
f(a)=biểu thức
giải f'(a)=0 suy ra f(a)<=f(0)=g(b)
giải g'(b)=0 suy ra g(b)<=g(0)=h©
khảo sát hàm g© suy ra g©<=g(1)

Có cách nào khác k dùng đạo hàm được k ạ? e chưa học

Cho x, y, z là các số thực dương. Chứng minh bất đẳng thức:

$ \frac{2x^{2}+xy}{(y+\sqrt{zx}+z)^{2}} + \frac{2y^{2}+yz}{(z+\sqrt{xy}+x)^{2}} + \frac{2z^{2}+zx}{(x+\sqrt{yz}+y)^{2}}\geq1$

Cho tứ giác lồi ABCD có M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.
CMR: ABCD là hình bình hành khi và chỉ khi $MP+ NQ= \frac{1}{2} ( AB+ BC+ CD+DA)$

Giải các PTsau:
$ 8 sin^{3} ( \frac{\pi}{3} - x) = sin 3x + 2 sin ( x- \frac{\pi}{3})+1$

(MCD) và (ABC); (MCB) và (ACD). Cho E thuộc BC, F thuộc BD. Xác định d là giao tuyến của ( MEF) và (ACD). Chứng minh d, CD, EF đồng qui

Đề hơi sai chút.
Lời giải:
Nhận xét:
\[
\begin{array}{l}
\tan \frac{A}{2} = \frac{r}{{p - a}} \\
\Rightarrow \sin A = \frac{{2\tan \frac{A}{2}}}{{\tan ^2 \frac{A}{2} + 1}} \Leftrightarrow \frac{a}{{2R}} = \frac{{2.\frac{r}{{p - a}}}}{{\left( {\frac{r}{{p - a}}} \right)^2 + 1}} \Leftrightarrow \frac{a}{{2R}} = \frac{{2r\left( {p - a} \right)}}{{r^2 + \left( {p - a} \right)^2 }} \\
\Leftrightarrow a\left( {r^2 + p^2 - 2ap + a^2 } \right) = 4rR\left( {p - a} \right) \\
\Leftrightarrow a^3 - 2pa^2 + \left( {r^2 + p^2 + 4Rr} \right)a - 4Rrp = 0 \\
\end{array}
\]
Tương tự, ta có $b,c$ cũng là nghiệm pt
\[
t^3 - 2pt^2 + \left( {r^2 + p^2 + 4Rr} \right)t - 4Rrp = 0
\]
Nên theo định lý Viete, ta có:
\[
\left\{ \begin{array}{l}
a + b + c = 2p \\
ab + bc + ca = r^2 + p^2 + 4Rr \\
abc = 4Rrp \\
\end{array} \right.
\]
(các hệ thức này được gọi là "bổ đề Viete trong tam giác" )
Áp dụng, ta có:
\[
\begin{array}{l}
a^2 + b^2 + c^2 - 2\left( {ab + bc + ca} \right) = \left( {a + b + c} \right)^2 - 4\left( {ab + bc + ca} \right) \\
= 4p^2 - 4\left( {r^2 + p^2 + 4Rr} \right) = - 16Rr - 4r^2 \\
\Rightarrow a^2 + b^2 + c^2 + 16Rr + 4r^2 = 2\left( {ab + bc + ca} \right) \\
\end{array}
\]

Tks bạn. đúng là đề thầy t cho sai thật.

Với mọi $\Delta ABC$ ta có:
$ a^{2}+b^{2} + c^{2} + 16r.R= 2(ab+bc+ca)$
Với r,R lần lượt là bán kính đường tròn nội tiếp, ngoại tiếp $\Delta ABC$

theo Chebyshev

$(a+b+c)(\frac{1}{\sqrt{a(b+c)}}+\frac{1}{\sqrt{b(c+a)}}+\frac{1}{\sqrt{c(a+b)}})\geq 3(\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}})$

$\Rightarrow \sqrt{\frac{b+c}{a}}+\sqrt{\frac{c+a}{b}}+\sqrt{\frac{a+b}{c}}\geq 2(\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}})$

Giải thích rõ hơn vì sao suy đc đpcm đi bạn

Cho $a,b,c>0$. CMR:
$\sqrt{\dfrac{a+b}{c}}+ \sqrt{\dfrac{b+c}{a}}+\sqrt{\dfrac{c+a}{b}} \geq 2(\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}})$

Bài 2 ý 1 bình phương

GHPT:

$$\left\{\begin{array}{l} x^2+y^2+xy+1=4y \\y(x+y)^2=2x^2+7y+2\end{array}\right.$$

hpt $$\Leftrightarrow\left\{\begin{array}{l} (x^2+1)+y(x+y)=4y \\y(x+y)^2-2(x^2+1)=7y\end{array}\right.$$

NX: y=0 không TM hệ

Với y#0 chia cả 2 vế của 2 pt cho y đc

$$\left\{\begin{array}{l} \frac{x^2+1}{y}+(x+y)=4 \\y(x+y)^2-2\frac{x^2+1}{y}=7\end{array}\right.$$

Đặt $$\left\{\begin{array}{l} \frac{x^2+1}{y}=a \\x+y=b\end{array}\right.$$ giải là xong.

1)
$\left\{\begin{matrix} y^2 + x + xy -6y + 1 = 0 & \\ y^3x - 8y^2 + x^2y + x = 0 & \end{matrix}\right.$

hpt

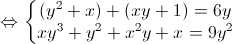
$\Leftrightarrow \left\{\begin{matrix} (y^2+x)+(xy+1) = 6y & \\ (x+y^2)(xy+1)= 9y^2 & \end{matrix}\right.$

Đặt $ a= x+y^2; b= xy+1$ hpt trở thành: $\left\{\begin{matrix} a+b = 6y & \\ ab= 9y^2 & \end{matrix}\right.$
$\Rightarrow$ a, b là nghiệm của pt : $t^2-6yt+9y^2 = 0$

$\Leftrightarrow t= 3y

\Leftrightarrow a=b= 3y

\Leftrightarrow \left\{\begin{matrix} y^2+x = 3y & \\ xy+1= 3y & \end{matrix}\right.

\Leftrightarrow \left\{\begin{matrix} x = 3y-y^2 & \\ y(3-y^2)+1=3y & \end{matrix}\right.

\Leftrightarrow \left\{\begin{matrix} x = 3y-y^2 & \\ y=1 & \end{matrix}\right.

\Leftrightarrow \left\{\begin{matrix} x = 2 & \\ y=1 & \end{matrix}\right.$

Gõ nhầm đừng kêu ^v^