$x \leqslant 3 $

Cho các số thực $-1\leqslant a_1,a_2,...,a_n\leqslant 1$
Tìm GTNN của $P=a_1(a_1+a_2+...+a_n)+a_2(a_2+a_3+...+a_n)+...+a_{n-1}(a_{n-1}+a_n)+a_{n}.a_n$

P = $\sum^n_{i = 1}a_i^2 + \sum_{i \neq j}a_ia_j$
$2P = 2\sum^n_{i = 1}a_i^2 + 2\sum_{i \neq j}a_ia_j$
$= \sum^n_{i = 1}a_i^2 + (\sum_{i = 1}^na_i)^2 \geqslant 0 + 0 = 0$
$\Rightarrow P \geqslant 0$
Dấu = xảy ra khi $a_i = 0
\forall i$

a)$I, K$ cách đều $AB, AC$ nên $I, K$ thuộc phân giác $\widehat{BAC}$
$\Rightarrow A, I, K$ thẳng hàng
b)Đường tròn $(I)$ tiếp xúc $AB, AC, BC$ tại $M, N, P$
$S_{ABC} = S_{IAB} + S_{IAC} + S_{IBC}$
$= \frac12(AB.IM + AC.IN + BC.IP)$
$= \frac12.r.(c + b + a)$ (1)
$S_{ABC} = S_{KAB} + S_{KAC} - S_{KBC}$
$= \frac12(KD.AB + KE.AC - KF.BC)$
$= \frac12.R(c + b - a)$ (2)
Nhân (1) và (2) vế theo vế ta được
$S_{ABC}^2 = \frac14.r.R.((c + b)^2 - a^2)$
$=\frac14.r.R.(c^2 + b^2 + 2bc - a^2)$
$=\frac12.b.c.r.R = S_{ABC}.r.R$
$\Leftrightarrow S_{ABC} = r.R$(đpcm)

a)
$(I)$ tiếp xúc $MN, HK$ tại $R, S$
$IR \perp MN, ID \perp HQ, MN // HQ$
$\Rightarrow R, I, D$ thẳng hàng (1)
tương tự $E, I, S$ thẳng hàng(2)
$N$ là giao điểm của 2 tiếp tuyến tại $R, E$ nên $IN$ là phân giác $\widehat{RIE}$ (3)
tương tự $IH$ là phân giác $\widehat{SID}$ )(4)
(1,2,3,4) $\Rightarrow N, I, H $ thẳng hàng (đpcm)
b)
$I$ là trung điểm $ES$
$\Rightarrow \triangle IEN = \triangle ISH$ (g, c, g)
$\Rightarrow NE = SH$ (5)
tương tự $EP = KS$ (6)
(5, 6) $\Rightarrow NP = KH$

Bổ đề: Cho 2 tam giác $ABC$ và $A'B'C'$ đồng dạng và cùng hướng
$M, M'$ lần lượt là trung điểm $BC, B'C'$
Cm góc giữa $AM, A'M'$ bằng góc giữa $AB, A'B'$
Cm b đ: Dựng tam giác $AB''C''$ bằng, có cạnh song song với tam giác $A'B'C'$, $M''$ trung điểm $B''C''$
có $\triangle ABC\sim \triangle AB''C''$
$\Rightarrow \frac{AB}{AB''} = \frac{BC}{B''C''} =\frac{BM}{B''M''}$
$\Rightarrow \triangle ABM\sim\triangle AB''M''$ (c, g, c)
$\Rightarrow \triangle ABB''\sim\triangle AMM''$ (c, g, c)
$\Rightarrow \widehat{BAB''} = \widehat{MAM''}$ (đpcm)

Cm:
$MN$ cắt $HK$ tại $J$
$\triangle AED\sim\triangle CFB$
$\Rightarrow \frac{AH}{HD} = \frac{CK}{KB}$
$\Rightarrow \frac{HM}{BD} =\frac{KN}{DB}$
$\Rightarrow HM = KN$
$\Rightarrow MHNK$ là hình bình hành
$\Rightarrow J$ là trung điểm $MN, HK$
Hạ $JI \perp AB$ cắt $EF$ tại $I$
$\Rightarrow I$ trung điểm $PQ$ (1)
Dựng các hình bình hành $JHEX, JKFY$
có $EX = FY$ và $EX // FY$
$\Rightarrow EXFY$ là hình bình hành
$EF$ cắt $XY$ tại $I'$
$\Rightarrow I'$ là trung điểm $EF, XY$
Dựng hình bình hành $ADBU$
$S$ trung điểm $UC$
$V$ trung điểm $AB, DU$
$\Rightarrow A, B, S $ thẳng hàng
Có $\frac{JX}{JY} = \frac{HE}{KF} = \frac{AD}{CB} = \frac{BU}{BC}$
có $\widehat{XJY} = \widehat{UBC}$ (góc có cạnh tương ứng vuông góc)
$\Rightarrow \triangle XJY\sim \triangle UBC$ (c, g, c)
Áp dụng bổ đề, ta có góc giữa $JI', BS$ bằng góc giữa $BU, JX$ bằng 90 độ
$\Rightarrow JI' \perp AB$
$\Rightarrow I \equiv I'$
$\Rightarrow I$ trung điểm $EF, PQ$
$\Rightarrow EP = FQ$ (đpcm)

Cho tam giác ABC ngoại tiếp (I) và (I) tiếp xúc BC tại D. Đường thẳng qua D vuông góc AI cắt đường trung bình ứng với đỉnh A của tam giác ABC tại R. J là trung điểm ID. CMR JR vuông góc AD

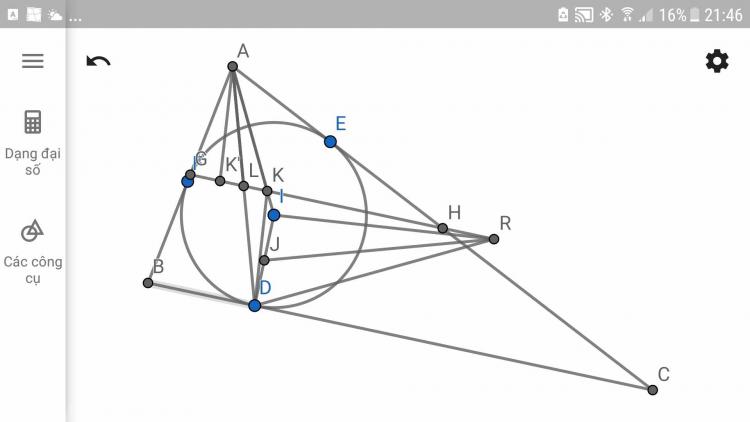
$AI, AD$ lần lượt cắt đường trung bình ứng đỉnh $A$ tại $K, L$
$K'$ đối xứng $K$ qua $L$
$\triangle KDR$ có $KI \perp DR, DI \perp KR$
$\Rightarrow I$ là trực tâm $\triangle KDR$
$\Rightarrow RI \perp KD$ (1)
ta có $L$ là trung điểm $AD, KK'$
$\Rightarrow AKDK'$ là hình bình hành
$\Rightarrow AK' // DK$ (2)
(1, 2) $\Rightarrow AK' \perp RI$ (3)
có $\widehat{K'AK} = \widehat{IRD}$ (góc có cạnh tương ứng vuông góc)
có $\widehat{AK'K} = \widehat{RID}$ (cạnh tương ứng vuông góc)
$\Rightarrow \triangle AK'K \sim \triangle RID$ (g, g) (4)
$\Rightarrow \frac{AK'}{RI} = \frac{K'K}{ID} =\frac{K'L}{IJ}$
$\Rightarrow \triangle AK'L \sim \triangle RIJ$ (c, g, c)
$\Rightarrow \widehat{K'AL} = \widehat{IRJ} $(5)
(3, 5) $\Rightarrow AL \perp JR$ (đpcm)

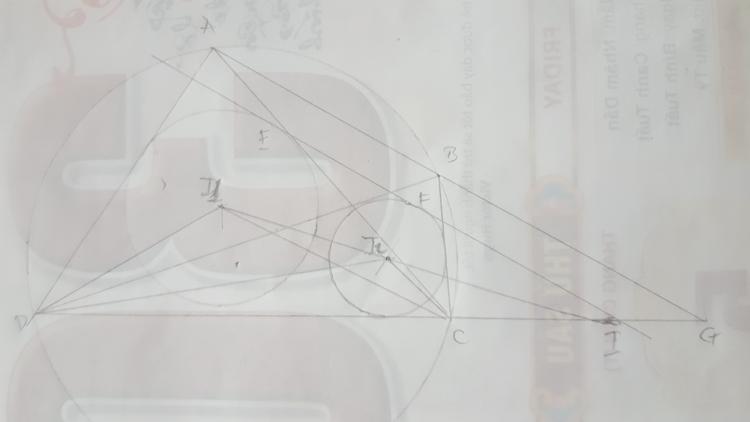
$I_1I_2$ cắt $CD$ tại $I$
Kẻ tiếp tuyến thứ 2 của $(I_1), (I_2)$ tiếp xúc $(I_1), (I_2)$ tại $E, F$
Ta có $E, F, I$ thẳng hàng
$AB$ cắt $CD$ tại $G$
Có $\widehat{I_1CI_2} = \widehat{I_2CD} - \widehat{I_1CD} = \frac12(\widehat{BCD} - \widehat{ACD}) = \frac12\widehat{BCA}$ (1)
Có $\widehat{I_1DI_2} = \widehat{I_1DC} - \widehat{I_2DC} = \frac12(\widehat{ADC} - \widehat{BDC}) =\frac12\widehat{ADB}$ (2)
Có $\widehat{ADB} = \widehat{ACB}$ (3)
(1, 2, 3) $\Rightarrow \widehat{I_1CI_2} = \widehat{I_1DI_2}$
$\Rightarrow I_1I_2CD$ nội tiếp
Ta có $\widehat{AGD} = \widehat{ABD} - \widehat{BDC} = \widehat{ACD} - \widehat{BDC}$ (4)
Có $\widehat{I_1ID} = \widehat{I_1CD} - \widehat{CI_1I_2} = \widehat{I_1CD} - \widehat{I_2DC} = \frac12(\widehat{ACD} - \widehat{BDC})$ (5)
Có $\widehat{EID} = 2\widehat{I_1ID}$ (6)
(4, 5, 6) $\Rightarrow \widehat{EID} = \widehat{AGD}$
$\Rightarrow AB // EI$ (đpcm)

h = (e, c)
e = i * h
c = j * h
Từ ch minh trên (bài #6) có (i, j) = 1 (1)
có (e, f) = 1
$\Rightarrow$ (i, f) = 1 (2)
(1), (2) $\Rightarrow$ (i, j * f) = 1
$\Rightarrow$ (h * i, h * j * f) = h
$\Rightarrow$ (e, c * f) = h = (e, c) (đpcm)
Ps: không biết có cách cm nào ngắn gọn hơn nữa không các bạn?

mình nhầm (a,bc)=(a,(a,b)c)

Gọi d = (a, b)
Đặt b = d * e
$\Rightarrow $ (a, e) = 1 (1)
(a, bc) = (a, (d * c) * e) (2)
Vì (1) $\Rightarrow$ (2) = (a, d * c) = (a, (a, b) * c) (đpcm)

(e, f) = 1
$\Rightarrow$ (e, f * c) = (e, c)
$\Rightarrow$ d * (e, f * c) = d * (e, c)

Gọi d = (a, b)
Đặt b = d * e
$\Rightarrow $ (a, e) = 1 (1)
(a, bc) = (a, (d * c) * e) (2)
Vì (1) $\Rightarrow$ (2) = (a, d * c) = (a, (a, b) * c) (đpcm)

Bạn giải thích cho mình chỗ "gọi d=(a,b). Đặt b=d*e thì (a,e)=1" được không bạn?

Bài giải trên mình làm sai rồi. Sai ngay chỗ bạn thắc mắc (a, e) = 1
Giải lại như sau
Đặt d = (a, b)
a = d * e
b = d * f
g = (e, f)
Nếu g > 1 suy ra a, b có ước chung d * g > d, => vô lí vì d là ước chung lớn nhất
=> (e, f) = 1
(a, b * c) = (d * e, d * f * c) = d * (e, f * c) = d * (e, c) = (d * e, d * c) = (a, (a, b) * c) (đpcm)

Chứng minh (a,bc)=(a,(a,b),c) với (a,bc) là ước chung lớn nhất của a và bc.

Đề có sai không nhỉ
Thử a = 2, b = 4, c = 3 là thấy sai rồi

Đặt z = (x, y)
x = z * i
y = z * j
k = (i, j)
Giả sử k > 1 => x, y có ước chung z * k > z => vô lí vì z là ước chung lớn nhất => (i, j) = 1 => $(i^2, j^2) = 1$
$(x^2, y^2) = (z^2*i^2, z^2*j^2)$
$=z^2 * (i^2, j^2) = z^2 = (x, y)^2$ (đpcm)

Cho $A$ là ma trận vuông cấp $n$. Chứng minh $det(A) = det(A^T) \quad(*)$

+Với $n = 2$

\[\begin{array}{l}
\det \left( A \right) = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\\
\det \left( {{A^T}} \right) = {a_{11}}{a_{22}} - {a_{21}}{a_{12}}\\
 \Rightarrow \det \left( A \right) = \det \left( {{A^T}} \right)
\end{array}\]

 

Giả sử (*) đúng với $n = k$ (1). Với $n = k + 1$, ký hiệu $A_{ij}$ là ma trận bù $a_{ij}$. Dễ thấy $(A_{11})^T = (A^T)_{11})$
$$(A_{1j})^T = (A^T)_{j1} \forall 1\leqslant j\leqslant n$$
Khai triển tính $det(A)$ theo hàng 1
\[\det \left( A \right) = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}{a_{1j}}\det \left( {{A_{1j}}} \right)} \quad \left( 2 \right)\]
Khai triển tính $det(A^T)$ theo cột 1
\[\det \left( {{A^T}} \right) = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}{a_{1j}}\det \left( {{{\left( {{A^T}} \right)}_{j1}}} \right)}  = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}} {a_{1j}}\det \left( {{{\left( {{A_{1j}}} \right)}^T}} \right) \quad \left( 3 \right)\]
Từ $(1), (2), (3)$ suy ra (*) đúng với $n = k + 1$
Vậy (*) đúng với mọi $n \geqslant 1$.

Qua $I$ kẻ đường thẳng vuông góc $OI$ cắt $AB, AC$ lần lượt tại $J, K$ (1)
Có $OIBJ$ nội tiếp $\Rightarrow \widehat{OJI} = \widehat{OBI}$ (2)
$\widehat{OBI} = \widehat{OCI}$ (3)
$OIKC$ nội tiếp $\Rightarrow \widehat{OCI} = \widehat{OKI}$ (4)
(2, 3, 4) $\Rightarrow \widehat{OJI} = \widehat{OKI}$ (5)
(1, 5) $\Rightarrow I$ là trung điểm $JK$ (6)
$\frac{IJ}{HM} = \frac{AI}{AH} = \frac{IK}{HN}$ (7)
(6, 7) $\Rightarrow HM = HN$ (đpcm)

Bổ đề: Cho $\triangle ABC$, $M$ nằm trong tam giác
$AM, BM, CM$ lần lượt cắt $BC, CA, AB$ tại $A_1, B_1, C_1$.
Cm $\frac{MA_1}{AA_1}\overrightarrow{AM} + \frac{MB_1}{BB_1}\overrightarrow{BM} + \frac{MC_1}{CC_1}\overrightarrow{CM} = \overrightarrow{0}$ (1)
Cm:
Kí hiệu $d(A, BC)$ là khoảng cách từ $A$ đến đường thẳng $BC$
ta có $\frac{MA_1}{AA_1} = \frac{d(M, BC)}{d(A, BC)} = \frac {d(M, BC).BC}{d(A, BC).BC} = \frac{S_{MBC}}{S_{ABC}}$
suy ra (1) $\Leftrightarrow \frac{S_{MBC}}{S_{ABC}}\overrightarrow{AM} + \frac{S_{MCA}}{S_{ABC}}\overrightarrow{BM} + \frac{S_{MAB}}{S_{ABC}}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{S_{MCA}}{S_{MBC}}\overrightarrow{BM} + \frac{S_{MAB}}{S_{MBC}}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{MC.d(A, MC)}{MC.d(B, MC)}\overrightarrow{BM} + \frac{MB.d(A, MB)}{MB.d(C, MB)}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{AC_1}{BC_1}\overrightarrow{BM} + \frac{AB_1}{CB_1}\overrightarrow{CM} = \overrightarrow{0}$ (2)
Qua $A$ kẻ đường thẳng // $BM$ cắt $CM$ tại $C_2$
qua $A$ kẻ đ th // $CM$ cắt $BM$ tại $B_2$
(2) $\Leftrightarrow \overrightarrow{AM} + \frac{AC_2}{BM}\overrightarrow{BM} + \frac{AB_2}{CM}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \overrightarrow{C_2A} + \overrightarrow{B_2A} = \overrightarrow{0}$ (3)
vì $AB_2MC_2$ là hình bình hành nên (3) đúng, suy ra (1) đúng (đpcm)

Cm:
$AB', AC', AD'$ lần lượt cắt $CD, DB, BC$ tại $B_2, C_2, D_2$
$AM$ cắt $mp(BCD)$ tại $N$
ta có $B, N, B_2$ thẳng hàng
$\overrightarrow{MB_1} = \frac{B'M}{B'B}\overrightarrow{BN}$ (4)
Áp dụng Menelauyt cho 3 điểm thẳng hàng $A, B', B_2$ và tam giác $BMN$, ta có
$\frac{B'M}{B'B}.\frac{B_2B}{B_2N}.\frac{AN}{AM} = 1$
$\Leftrightarrow \frac{B'M}{B'B} = \frac{AM}{AN}.\frac{B_2N}{B_2B}$ (5)
(4, 5) $\Rightarrow \overrightarrow{MB_1} = \frac{AM}{AN}.\frac{B_2N}{B_2B}.\overrightarrow{BN}$
tương tự với $\overrightarrow{MC_1}, \overrightarrow{MD_1}$
có $\overrightarrow{MB_1} + \overrightarrow{MC_1} + \overrightarrow{MD_1}$
$= \frac{AM}{AN}.(\frac{B_2N}{B_2B}.\overrightarrow{BN} + \frac{C_2N}{C_2C}.\overrightarrow{CN} + \frac{D_2N}{D_2D}.\overrightarrow{DN})$
$= \frac{AM}{AN}.\overrightarrow{0}$ (theo bổ đề)
$= \overrightarrow{0}$
vậy, $M$ là trọng tâm của $\triangle B_1C_1D_1$ (đpcm)

a)
Hạ $HL$ vuông góc $AC$ tại $L$ và cắt $AK$ tại $M$
Đặt $\frac{AB}{AC} = x$
$\frac{AL}{CL} = \frac{AL}{HL}.\frac{HL}{CL} = x^2$
$\Rightarrow \frac{AL}{AC} = \frac{x^2}{x^2 + 1}$
$\Rightarrow \frac{AL}{AN} = \frac{4x^2}{x^2 + 1}$
$AB = AI + BI = IH(\frac1x + x) = xAC$
$\Rightarrow \frac{AC}{IH} = \frac{x^2 + 1}{x^2}$
$\frac{PN}{PH} = \frac{ND}{IH} = \frac{x^2 + 1}{4x^2}$
Áp dụng Menelauyt cho 3 điểm thẳng hàng $A, P, M$ và tam giác $HNL$, có
$\frac{AL}{AN}.\frac{PN}{PH}.\frac{MH}{ML} =1$
$\Rightarrow \frac{MH}{ML} = 1$
Ta có $\triangle BAC\sim\triangle ALH$ {g, g)
$\Rightarrow \frac{BA}{AL} = \frac{AC}{LH} = \frac{2AD}{2LM} = \frac{AD}{LM}$
$\Rightarrow \triangle BAD\sim\triangle ALM$ (c, g, c)
$\Rightarrow \widehat{ABD} = \widehat{LAM} = 90^\circ - \widehat{ADB}$
$\Rightarrow AL\perp BD$(đpcm)

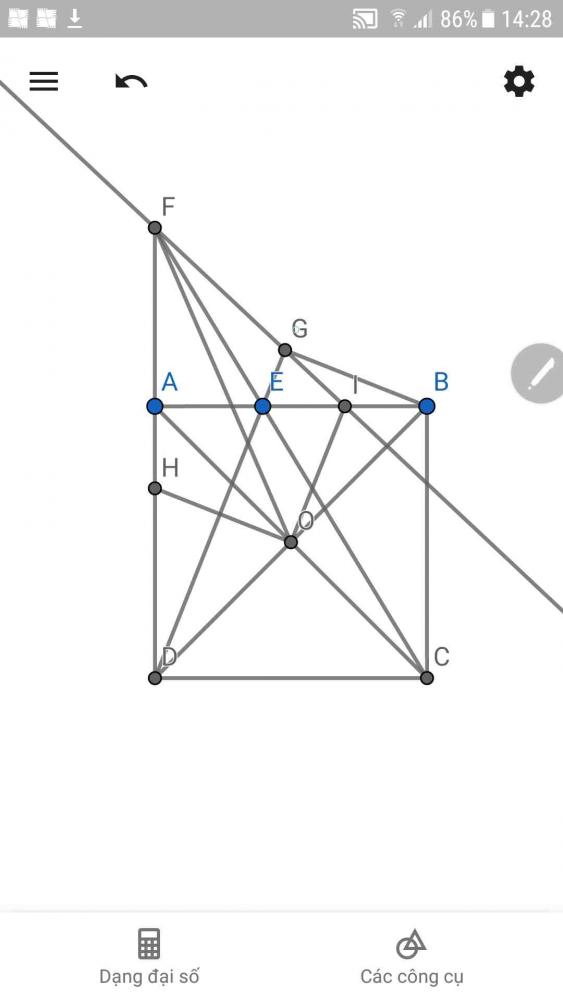
a)
Lấy $J$ trên đoạn $AD$ sao cho $AJ = BI$
$\Rightarrow \triangle OAJ = \triangle OBI$ (c, g, c)
$\Rightarrow OJ = OI$ (1)
Đặt $AE = x, AB = a$
Có $AI = AE + EI = x + \frac12EB = x + \frac12(a - x) = \frac{a + x}2$
Có $\frac{FA}{FD} = \frac{AE}{DC} = \frac xa$
$\Leftrightarrow \frac{FA}{FD - FA} = \frac x{a - x}$
$\Leftrightarrow FA = \frac {ax}{a - x}$
Có $FI^2 = FA^2 + AI^2$
$= \frac{a^2x^2}{(a - x)^2} + \frac{(a + x)^2}4$
$= \frac{4a^2x^2 + (a^2 - x^2)^2}{4(a - x)^2}$
$= \frac{(a^2 + x^2)^2}{4(a - x)^2}$
$\Leftrightarrow FI = \frac{a^2 + x^2}{2(a - x)}$ (2)
Có $FJ = FA + AI = \frac{ax}{a - x} + \frac{a - x}2$
$= \frac{2ax + (a - x)^2}{2(a - x)} = \frac{a^2 + x^2}{2(a - x)}$ (3)
(2, 3) $\Rightarrow FI = FJ$ (4)
(1, 4) $\Rightarrow \triangle OFJ = \triangle OFI$ (c, c, c)
$\Rightarrow \widehat{OFJ} = \widehat{OFI}$
$\Rightarrow O$ cách đều $FD, FI$
$\Rightarrow FI$ luôn tiếp xúc đường tròn nội tiếp $ABCD$
b)
Gọi tia $FI$ là tia $Fx$, cắt $DE$ tại $G$
theo a), $O$ cách đều $BA, Fx$
$\Rightarrow \widehat{OIA} = \widehat{OIx}$
$\Leftrightarrow \widehat{IEG} = \widehat{IGE}$
$\Rightarrow IE = IG = IB$
$\Rightarrow \widehat{DGB} = 90^\circ = \widehat{DAB}$
Vậy, $G$ nằm trên đường tròn ngoại tiếp $ABCD$ (đpcm)

Dựng hình chữ nhật $XBX'_1N$ tâm $D$
Dựng hcn $XCX'N$ tâm $E$
Lấy $A'$ đối xứng $A$ qua $M$
$\Rightarrow N$ là tâm nội tiếp $\triangle A'BC$
$\widehat{BA'C} = \widehat{BAC} = \widehat{BAH} + \widehat{CAH} $
$= \widehat{BCH} + \widehat{CBH} = 180^\circ - \widehat{BHC}$
$\Rightarrow A'\in (HBC)$
$X'Y$ cắt $X'_1Z$ tại $F$
$NY \perp PC \Rightarrow Y \in (E, EC)$
$\Rightarrow EK$ là trung trực $XY$
$\Rightarrow EK // X'F$
tương tự, $DK // X'_1F$
$\Rightarrow \widehat{DKE} = \widehat{X'_1FX'} = 180^\circ - \widehat{YXZ}$
+xét $P, A'$ cùng phía với $BC$

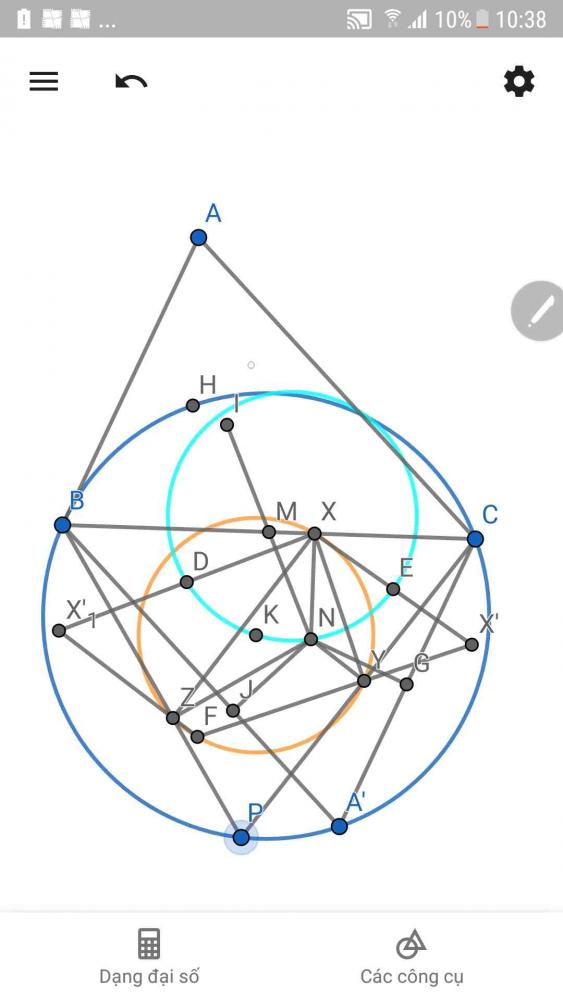
$\widehat{YXZ} = \widehat{YXN} + \widehat{NXZ}$
$= \widehat{YCN} + \widehat{NBZ}$
$= \widehat{A'CN} - \widehat{A'CP} + \widehat{NBA'} + \widehat{A'BP}$
$= \frac12\widehat{B} + \frac12\widehat{C}$
Khi $P \equiv A'$ thì $K \equiv N$ và $\widehat{DKE} = \widehat{DNE} = 180^\circ - \frac12\widehat{B} - \frac13\widehat{C}$
$\Rightarrow K \in (DNE)$ cố định
+xét $P, A'$ khác phía với $CB$


$\widehat{YXZ} = 180^\circ - \widehat{YXC} - \widehat{ZXB}$
$= 180^\circ - \widehat{YGC} - \widehat{ZJB}$
$= 180^\circ - \widehat{ECG} - \widehat{DBJ}$
$= 180^\circ - \frac12\widehat{B} - \frac12\widehat{C} = \widehat{DNE}$
$\Leftrightarrow 180^\circ - \widehat{DKE} = \widehat{DNE}$
$\Rightarrow \widehat{DKE} + \widehat{DNE} = 180^\circ$
$\Rightarrow K \in (DNE)$
đpcm

Dựng các tiếp tuyến chung của hai đường tròn (O ; 2cm) và (O' ; 1cm) biết OO' = 5cm trong các trong các trường hợp sau : a) Tiếp tuyến chung không cắt đoạn thẳng OO'. b) Tiếp tuyến chung cắt đoạn thẳng OO'.

Dễ thấy (O), (O') nằm ngoài nhau
Giả sử tiếp tuyến chung tiếp xúc (O;2) tại A, (O';1) tại B
Hạ BH vuông góc OA tại H
a)+ Phân tích:OH = OA - AH = OA - OB = 2 -1 = 1
+ Cách dựng:
- Dựng đường tròn đường kính OO'
- Dựng đường tròn tâm O bán kính 1 cắt đường tròn trên tại H
- OH cắt (O) tại A
- qua O' dựng đường thẳng // OA cắt (O') tại B nằm cùng phía với A so với OO'
+ Chứng minh: Bạn tự cm
+ Biện luận : Bài toán có 2 nghiệm hình
b)Cách dựng:
- Dựng đ tròn đ kính OO'
- Dựng đ tròn tâm O b kính 2 + 1 = 3 cắt đ tròn trên tại H
- OH cắt (O) tại A
- qua O' dựng đ thẳng // OA cắt (O') tại B khác phía với A so với OO'
+Biện luận : Bài toán có 2 nghiệm hình

$n = \left(\overline{a_{t-1}...a_2a_1a_0}\right)_p$
$= a_{t-1}p^{t-1} + ... + a_2t^2 + a_1t + a_0$
Vì n có t chữ số hệ p phân nên $a_{t-1} \geqslant 1, a_i \geqslant 0 \forall i, 0 \leqslant i < t - 1$
$\Rightarrow n \geqslant p^{t-1}$
Lấy $log_p$ 2 vế được
$log_pn \geqslant log_pp^{t-1} = t - 1$ (đpcm)

Không biết đúng hay sai nữa

Đã tìm ra đáp án https://www.google.c...gBiHjqIAB1uXgCu

Bạn nghiên cứu ở đây nha: https://en.wikipedia...liptic_integral

Trang đó khó hiểu quá
Các bạn có ai giải được trường hợp cụ thể bên trên không? Còn nữa, nếu f(y) = tích phân hàm trên với cận dưới là hằng số c và cận trên là y thì hàm f trên có thể là elementary function không?

Tính tích phân của hàm $f(x) =\sqrt{ax^4 + bx^3 + cx^2 + dx + e}$
Cận từ $m$ đến $n$ với $0 \le m < n \le 1$

Các bạn cho biết cách tính trường hợp cụ thể cũng được
Tính $\int_0^1\left(\sqrt{x^4 + 2x^3 + 3x^2 +7x + 9}\right)dx$