Cho x,y,z (x,y,z 0) thỏa mãn:
x+y+z=3 và xy+yz+zx=1
Tìm min và max của P=xyz

http://www.math.vn/s...31932#post31932

Chuẩn bị sang năm 2011 rồi mà diễn đàn mình vẫn còn mấy mục Các kỳ thi VMO, TST, IMO năm 2009 , Kỳ thi tốt nghiệp và tuyển sinh đại học 2009 lỗi thời quá. Còn cái Trại hè Toán học 2010 không tổ chức vì vậy nên đóng cái mục này lại hoặc xóa đi

CMR: $ \dfrac{(a+1)(a+2)(a+3)(a+4)}{16a^2} \geq 2 \sqrt{6} (a>0) $. Em thử áp dụng BĐT Cauchy nhìu lần r�#8220;i nhân lại thì ra nhưng ko tìm được đẳng thức xảy ra khi nào. Xin các bác chỉ giáo

$ \dfrac{(a+1)(a+2)(a+3)(a+4)}{16a^2} > \dfrac{(2 \sqrt {a})(2 \sqrt {2a})(2 \sqrt {3a})(2 \sqrt {4a})}{16a^2} =\dfrac{32 \sqrt {6}a^2}{16a^2} =2 \sqrt{6}$

Đẳng thức không xảy ra

Mạo muội đưa ra lời giải bằng Cauchy ngược :

$ \dfrac{1}{(1+a)(1+a^2)}=\dfrac{1}{1+a}-\dfrac{a^2}{(1+a)(1+a^2)} \ge\dfrac{1}{1+a}- \dfrac{a}{2(1+a)} =\dfrac{3}{2(1+a)} -\dfrac{1}{2} $

$ \dfrac{3}{2(1+a)}+\dfrac{3}{2(1+b)}+\dfrac{3}{2(1+c)}+\dfrac{3}{2(1+d)} \ge \dfrac{6}{\sqrt[4]{(1+a)(1+b)(1+c)(1+d) }} \ge 3 $

suy ra

$ \dfrac{1}{(1+a)(1+a^2)} + \dfrac{1}{(1+b)(1+b^2)} + \dfrac{1}{(1+c)(1+c^2)} + \dfrac{1}{(1+d)(1+d^2)}\ge 1$

$ \dfrac{6}{\sqrt[4]{(1+a)(1+b)(1+c)(1+d) }} \ge 3 $

Chỗ này ngược dấu rồi Vin ơi.
Chú ý dùng BDT Holder ta có $(1+a)(1+b)(1+c)(1+d) \ge (1+\sqrt[4]{abcd})^4=2^4$ nên

$ \sqrt [4]{(1+a)(1+b)(1+c)(1+d)} \ge 2$ Do đó không thể có đánh giá trên được

AI giúp em một khúc mắc nhỏ này với
CHo $a;b;c > 0$
Chứng minh $(a+b+c)^2-9ab>0$

Cho $a=b=1$ ; $c=0,1$ thấy ngay đề sai

Đây em

Lên non xuống chức mấy lần,giờ đã về vườn thành hiệp sĩ trồng rau xanh

Theo mình THTT nên cắt bớt mấy cái mục cho cấp THCS đi,vì chuyện đó nên dành cho TTT2.Ví như chuyên mục giới thiệu đề thi vào 10 THPT (TTT2 cũng có mục này rồi) nên thay bằng các đề thi học sinh giỏi lớp 10,11,12 ,đề chọn đội tuyển thi VMO các tỉnh thành,....Bài viết dành cho THCS cũng nên giảm bớt (Vì cái này ở TTT2 mỗi số cũng có nhiều bài rồi) nên thay bằng các bài hướng dẫn các phương pháp giải toán cho THPT,...

Một điều nữa là phần thi giải toán đề ra kỳ này có lẽ là phần được nhiều bạn trẻ quan tâm nhất nhưng mà thưởng ít quá (như TTT2 mỗi số thưởng tiền ngay cũng hay) . Cả năm THTT mới tổng kết và thưởng một lần.Giải XS với giải nhất thì ko nói nhưng mấy giải còn lại có thể là cái máy tính loại ít tính năng hay thưởng 1-2 cuốn sách (Cộng lại được vài chục - nếu mua ở hiệu sách có khi được giảm giá còn độ 2-3 chục nghìn) kể ra thật ít với công sức bỏ cả năm trời ra để gửi bài.
Đành rằng phần thưởng hay tiền không phải là vấn đề chính nhưng nó cũng phần nào động viên và tăng hứng thú cho các bạn tham gia.

Với giá bán 8000 VND hiện nay(trong khi chưa thấy tăng số trang ,...) liệu có phù hợp.Với các bạn thành phố thì không nói,nhưng với các bạn miền quê khi khác.

Nói thì không ai tin nhưng anh trai mình ngày xưa không có tiền đặt báo ở bưu điện,mượn bạn được quyển báo,(hồi đó ở quê không có hiệu photo) nhưng mà phải sớm trả,thế là ngồi cặm cụi chép tay lại cả quyển báo luôn .Đến thời mình nhìn quyển báo đó mà thực sự nể

Chứng minh dùm các định lí sau:
1. Hạng của ma trận không thay đổi qua các phép biến đổi sơ cấp.
2. i. Nếu A, B là các ma trận cấp mxn thì rank(A+B) rankA+rankB
ii. Nếu A là ma trận cấp mxn, B là ma trận cấp nxp thì rank (AB) min{rankA,rankB}
iii. Nếu A là ma trận cấp mxn, X là ma trận khả nghịch cấp n, Y là ma trận khả nghịch cấp m thì rankA=rank(AX)=rank(YA)
3. Cho A, B là ma trận cấp mxn. Nếu A đồng dạng với B thì rankA = rankB

Gợi ý
Câu 1 thì áp dụng các hệ thức quen biết chỉ ra các phép biến đổi không làm thay đổi tính khác không hay bằng không của các định thức con của một ma trận -> không làm thay đổi hạng ma trận

Câu 2.i
Giả sử A,B là các ma trận cấp $m \times n$ và $f: V \rightarrow W$
$g: V \rightarrow W$ là các ánh xạ tuyến tính nhận A,B là các ma trận biểu diễn
(V,W là các không gian n,m chiều)

$rank(A+B) =dim((f+g)V)=dim(f(V)+g(V))$
$=dim(f(V)+dimg(V)-dim(f(V) \cap g(V))$

$\le dim(f(V)+dimg(V)=rank(A)+rank(B)$

ii.Mỗi dòng của $AB$ biểu diễn tuyến tính qua các dòng của $B$
Mỗi cột của $AB$ biểu diễn tuyến tính qua các cột của $A$
nên $rank(AB) \le rank(A)$ ; $rank(AB) \le rank(B)$ .Ta có đpcm
iii.Áp dụng các BĐT về hạng của ma trận

3.Vì $A,B$ đồng dạng nên có thể viết
$A=Q^-1B.Q$
$B=P^-1.A.P$
Áp dụng BĐT ở trên dễ suy ra $rank(A) \le rank(B)$ và $rank(B) \le rank(A)$
Suy ra đpcm

Hix, chả hiểu sao càng ngày thấy báo THTT càng ít lôi cuốn....Nhiều bài viết không hấp dẫn lắm.

Mathvn chơi Scan cả số báo luôn nữa. Không biết có vi phạm cái gì không.

THTT nay thương mại hóa ghê quá anh. Bài gửi thì chả thấy đăng mà còn đăng bài sai đề nữa, không bik là tòa soạn cố tình hay là làm mới theo kiểu đấy nữa.
Giờ kiếm cái tài khoản trong pege của Crux doalw báo rồi gửi bài luôn bằng email cho nhanh. Vừa làm toán vừa học anh lun.

Hic,cả năm rồi anh ko đọc báo,tháng trước ra mua quyển báo đã thấy giá 8 nghìn Việt Nam đồng

$VT\le (\sqrt{6(a+b+c)})^2$
nên ta sẽ CM:$9\prod (a+b)\ge 8(\sum ab)(\sum a)$ (đúng)

Anh Magus quên chưa lột non chú tuan101293

2) Hình vuông sau có 16 ô : hãy xếp các số từ 1 đến 16 vào các ô để dược
tổng của mỗi hàng, mỗi cột, hai đường chéo đều bằng 34 :
( tìm ra các phương án khác nhau )
Ví dụ :

1 15 14 4
12 6 7 9
5 11 10 8
16 2 3 13

1 + 15 + 14 + 4 = 12 + 6 + 7 + 9 = 5 + 11 + 10 + 8 = 16 + 2 + 3 + 13 = 34
1 + 12 + 5 + 16 = 15 + 6 + 11 + 2 = 14 + 7 + 10 + 3 = 4 + 9 + 8 + 13 = 34
1 + 6 + 10 + 13 = 16 + 11 + 7 + 4 = 34

Mở rộng bài toán cho hình vuông có 25, 36 . . . ô

Mình suy nghỉ hoài mà giải chưa được, nhức đầu quá. ai pro thi giải dùm mình thuật toán. mình cám ơn nhiều.

liên hệ : [email protected]

Đây là bài toán về ma trận kì ảo,giải bài này thì có thể viết theo thứ tự
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16

Sau đó đổi chỗ các số đầu và cuối của các đường chéo cho nhau,


16 2 3 13
5 6 7 8
9 10 11 12
4 14 15 1

đổi chỗ 2 số ở vị trị thứ 2 và 3 mỗi đường chéo cho nhau ta được
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Ta được ma trận vuông cấp 4 thỏa mãn bài toán
Ngoài ra còn 1 số đáp án khác ,bạn đọc thêm ở đây http://vi.wikipedia....

và đây nữa http://hauionline.co...hread.php?t=494

Lương Thế Vinh,Vũ Hữu,... đều được đặt tên đường hết rồi.Chắc sắp tới ở một nơi nào đó của Việt Nam sẽ có con đường mang tên Ngô Bảo Châu.

Bài 2
Chua hóa abc=1
Đặt $ a=x^3;... =>xyz=1$
bất đẳng thức $ => \sum{\dfrac{1}{x^3+y^3+1}}\le 1$ (dễ rồi $ x^3+y^3 \geq xy(x+y)$ )

Đề cho $0 \le a,b,c \le 1$ nên $abc \le 1$ (Đẳng thức xảy ra khi $a=b=c=1$).Chuẩn hóa $abc=1$ khác nào cho luôn $a=b=c=1$.Em chưa hiểu về chuẩn hóa rồi,đừng dùng bừa bãi

hạn giải bài chưa hết nên đề nghị ban quản lí khóa topic này lại

Mod bị cắt chức hết rồi ,đợi mấy Admin vậy

Cm: 333^{222} +222 ^{333} 13

$333 \equiv 8 (mod 13)$

$333^{222 }\equiv 8^{6.37} \equiv (-1)^{37 } \equiv (-1) (mod 13)$ (Chú ý $8^6 \equiv (-1) (mod 13)$)

Lại có $222 \equiv 1 (mod 13)$ nên $222 ^{333} \equiv 1 (mod 13)$
Suy ra đpcm

Cho em hỏi câu này làm thế nào với ạ?

Em có thể giải như sau

Ta có
$sinnx-sin(n-2)x=2cos(n-1)x. sinx$ hay $\dfrac{sinnx}{sinx} - \dfrac{sin(n-2)x}{sinx} =2cos(n-1)x$ ($n \ge 2$)
Lấy tích phân 2 vế trên đoạn $[0;\pi]$ ta có

$I_n=I_{n-2}$ (chú ý $\int _0^{\pi} cos(n-1)xdx=0$

Vậy nếu $n$ lẻ thì $I_n=I_1$
$n$ chẵn thì $I_n=I_0$

Đọc sáng tạo BĐT PKH có ghi:
$ x^5 + y^5 \ge x^2 y^2 \left( {x + y} \right)$
với x, y dướng.
Cho em hỏi vì sao vậy?

Xét hiệu $x^5+y^5-x^2y^2(x+y)=x^3(x^2-y^2)-y^3(x^2-y^2)$
$=(x^2-y^2)(x^3-y^3)=(x-y)^2(x+y)(x^2+xy+y^2) \ge 0$

Cho a,b,c >0, abc=1 CM:
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{6}{a+b+c}\ge 5$

Dồn biến

$f(a,b,c) - f(a,\sqrt{bc},\sqrt{bc}) = (\sqrt{b}-\sqrt{c})^2(\dfrac{1}{bc}-\dfrac{6}{(a+b+c)(a+2\sqrt{bc})})$
Giả sử $a=max\{a,b,c\}$ thì $a \ge \sqrt{bc}$
nên $(a+b+c)(a+2\sqrt{bc}) \ge 3\sqrt{bc}.3\sqrt{bc} =9bc$

$ \rightarrow \dfrac{6}{(a+b+c)(a+2\sqrt{bc})} \le \dfrac{2}{3bc} < \dfrac{1}{bc}$

Do đó $f(a,b,c) \ge f(a,\sqrt{bc},\sqrt{bc}) $

Đặt $t=\sqrt{bc}$
ta đưa về chứng minh BĐT 1 biến theo t
$t^2+\dfrac{2}{t}+\dfrac{6t^2}{1+2t^3} \ge 5$
Đến đây thì đơn giản rồi

cho em hỏi dịch trang mathlinks sang tiếng việt mình ntn?

Em thử dùng trình duyệt Google Chrome xem

Chờ đợi cái tên Ngô Bảo Châu được xướng lên...
Ngày mai 19/8, tên những nhà toán học được trao giải thưởng danh giá Fields sẽ được công bố tại lễ khai mạc Đại hội Toán học thế giới tại Hyderabad, Ấn Độ. Việt Nam đang chờ đợi cái tên Ngô Bảo Châu được xướng lên...
>> ìNếu được nhận giải thưởng Fields, tôi sẽ dành tặng học sinh nghèo”


GS Ngô Bảo Châu

Cứ bốn năm một lần, Giải thưởng Fields - giải thưởng được xem như giải Nobel trong lĩnh vực toán học, dành cho những nhà toán học không quá 40 tuổi vào năm trao giải - được trao tại các kì Đại hội Toán học thế giới.

Theo GS.TSKH Trần Văn Nhung, nếu GS Ngô Bảo Châu (sinh năm 1972) vinh danh nhận giải thưởng này thì Việt Nam không chỉ nằm trong Top 10-15 Olympic Toán phổ thông quốc tế mà còn nằm trong Top 11-12 nước của thế giới được nhận Giải thưởng Fields.

Trao đổi với phóng viên, trước khi lên đường sang Ấn Độ dự Đại hội Toán học, GS Ngô Bảo Châu khiêm tốn cho biết: ìCác đại hội Toán học thế giới từ trước đến nay, đa số nhà khoa học dưới 40 tuổi được mời báo cáo toàn thể ở Đại hội đều được trao Giải thưởng Fields tại Đại hội đó. Lần này chỉ có hai nhà khoa học, tôi và một người Brazil, dưới 40 tuổi được báo cáo tại phiên toàn thể.

Tôi có báo cáo tổng thể tại đại hội tổng hợp từ hơn 10 báo cáo. Ngoài ra, đại hội còn các báo cáo chuyên ngành. Mỗi ngành có 5 - 7 báo cáo. Đây là những báo cáo rất tốt đánh dấu sự phát triển của mỗi ngành như hình học, đại số... Mỗi người được mời báo cáo tại đại hội, họ rất hãnh diện và làm báo cáo rất tốt, thường các báo cáo từ 10 - 20 trang và nói rất sát chất lượng của từng ngành toán học trong thời gian vừa qua. Qua báo cáo này mọi người nắm rất rõ về sự phát triển toán học.
Nói về công trình ìBổ đề cơ bản”, GS. Ngô Bảo Châu cho biết: ìThực sự những người nghiên cứu toán học vẫn không hiểu nổi tác dụng của ìBổ đề cơ bản”. Vì bản thân ì Bổ đề cơ bản” tương đối kỹ thuật nằm trong chương trình Langland cơ bản toán học của thế kỷ 20. Chương trình vĩ đại, có mục tiêu rõ ràng nhưng khó đến. Hầu hết những phần của chương trình Langland, có rất nhiều công trình phụ thuộc vào ìBổ đề cơ bản” nên ìBổ đề cơ bản” càng càng ngày quan trọng nếu không có nó thì nhiều công trình khác sụp đổ. Có cái hay khi tôi chứng minh ìBổ đề cơ bản”, tôi dùng nhiều bài báo có liên quan đến phần lý thuyết nên một số nhà vật lý rất quan tâm đến Bổ đề này”.

Nếu GS Ngô Bảo Châu được tôn vinh, không có gì là bất ngờ!

Trao đổi với Dân trí, GS.TSKH Lê Tuấn Hoa, Phó Viện trưởng Viện Toán học Việt Nam vui mừng cho biết: ìGiới toán học thế giới ít ai có thể ngờ rằng, ìBổ đề cơ bản” lại được chứng minh một cách chóng vánh như vậy. Đó là một kỳ tích, thành tích vĩ đại của nền Toán học. Bổ đề này không chỉ đóng vai trò đặc biệt quan trọng trong phát triển Toán học mà còn liên quan đến những ngành khác, đặc biệt là Vật lý lý thuyết”.


GS Ngô Bảo Châu - niềm tự hào của Việt Nam.

Theo GS. Lê Tuấn Hoa, để thấy tầm quan trọng của Bổ đề cơ bản của Chương trình Langlands, ta chỉ cần nhớ lại sự kiện Andrew Wiles đã chứng minh được Định lí lớn Fermat cách đây 15 năm - một định lí nổi tiếng mà sau hơn 300 năm nghiên cứu của nhiều thế hệ toán học lừng danh trên thế giới mới được giải quyết. Theo một nghĩa nào đó, thành công của Wiles dựa trên việc chứng minh được một trường hợp riêng của Bổ đề cơ bản. Nhờ đó Andrew Wiles đã được trao một Đĩa bạc đặc biệt tại Đại hội Toán học thế giới năm 1998, được xem như Giải thưởng Fields (Giải thưởng Fields chỉ trao cho nhà toán học không quá 40 tuổi, mà khi đó Wiles đã 45 tuổi, nên Liên đoàn toán học trao Đĩa bạc đặc biệt để tránh vi phạm luật).

Dưới tên là ìBổ đề cơ bản”, nhưng đây là một Giả thuyết tức là một dự đoán - do Robert Langlands đưa ra vào những năm 60, và sau đó được diễn đạt dưới dạng tổng quát trong một công trình chung của Robert Langlands và Diana Shelstad vào những năm 70. Do vai trò đặc biệt quan trọng của Bổ đề cơ bản, rất nhiều nhà toán học tài ba đã tập trung sức lực tấn công nó và đã chứng minh được một số trường hợp riêng.

Trường hợp riêng quan trọng nhất lại cũng chính do Bảo Châu cùng thầy hướng dẫn luận án Tiến sĩ của mình là GS. Gerard Laumon chứng minh vào năm 2004. ìChỉ với” kết quả riêng đó, năm 2004 hai nhà toán học này đã được trao một trong những giải thưởng danh giá trong Toán học: Giải thưởng Clay.

Tuy nhiên, để chứng minh trọn vẹn Bổ đề cơ bản thì nhiều người nghĩ rằng phải cần một thời gian dài nữa. Nhưng với Ngô Bảo Châu thì không! Sau công trình đạt Giải thưởng Clay, anh đã mạnh dạn theo đuổi con đường của mình và đã tìm ra chìa khóa để giải nó.

Năm 22 tuổi, khi đó đang du học bên Pháp tại trường đại học danh giá nhất nước Pháp, Ngô Bảo Châu đã ìbập” ngay vào đề tài nghiên cứu khó nhất. Đó là là một phần của Chương trình Langlands. Như vậy, mặc dù còn rất trẻ (năm nay GS Ngô Bảo Châu 38 tuổi), nhưng anh đã có 15 năm nghiên cứu vấn đề này. Bằng tài năng xuất chúng của mình, trong thời gian học tập, nghiên cứu, và làm việc cật lực, Ngô Bảo Châu đã đưa ra nhiều ý tưởng mới độc đáo. Anh liên tục làm cho thế giới Toán học ngạc nhiên.

Đỉnh điểm là đầu năm 2008, GS. Châu công bố một chứng minh hoàn chỉnh cho bổ đề cơ bản trong trường hợp tổng quát cho các đại số Lie. Lúc đầu công trình ìchỉ khoảng” 150 trang. Sau khi lược bỏ bớt những điều không phục vụ trực tiếp cho chứng minh Bổ đề cơ bản và diễn giải chi tiết hơn, công trình dài thành 188 trang! Dù ý tưởng chứng minh rất rành rọt, các nhà Toán học đầu đàn phải mất hơn 1 năm để kiểm chứng các chi tiết của nó!

Đây là một kỳ tích vĩ đại của nền toán học thế giới - GS. Lê Tuấn Hoa khẳng định và không ai nghi ngờ điều đó. Ngay giới Toán học Việt Nam cũng được hân hạnh biết điều này từ hơn một năm trước, khi GS Châu báo cáo tóm lược ý tưởng của công trình này tại Đại hội Toán học Việt Nam lần thứ 7 tại Quy Nhơn vào tháng 8 năm 2008. Cho nên việc anh được tôn vinh không có gì bất ngờ.

Thế nhưng việc được tạp chí Time đưa vào bình chọn là một trong 10 khám phá khoa học quan trọng nhất của năm 2009 thì quả là ngạc nhiên. Ngạc nhiên bởi vì rất ít khi một công trình Toán học được Time để ý đến! Lần gần đây nhất Time để ý đến Toán học chính là xếp công trình của nhà Toán học Nga Perelman - người được Giải thưởng Fields năm 2006 là thành tựu quan trọng nhất trong lĩnh vực khoa học công nghệ năm 2006

Giờ đây, chúng ta hồi hộp mong chờ giây phút GS. Ngô Bảo Châu được trao giải Field vào ngày mai 19/8, như thế, đây sẽ đánh dấu sự kiện lịch sử trong nền Toán học, không chỉ của Việt Nam mà cả trên thế giới.

Nguồn : Dân trí

Cmr: $sinA+sinB+sinC \geq sin^3A+sin^3B+sin^3C+sinA.sinB.sinC$ voi moi tam giac $ABC$.

Hoi cu nhung hay

Áp dụng $sin3x=3sinx-4sin^3x$ hay $sin^3x=\dfrac{1}{4}(3sinx-sinx)$

ta đưa BĐT cần chứng minh về dạng

$\sum sinA+\sum sin 3A \ge 4 \Pi sin A$ (1)

Tiếp tục sử dụng các hệ thức lượng giác quen thuộc
$cos 3x=4cos^3 x -3cosx$ ,$sin 2x = 2sinxcosx$
$\sum sin A = 4 \Pi cos(\dfrac{A}{2})$
$\sum sin 3A = - 4 \Pi cos(\dfrac{3A}{2})= -4 \Pi (4cos ^2 \dfrac{A}{2}- 3cos \dfrac{A}{2})$
$=-4 \Pi cos \dfrac{A}{2} \Pi (4cos ^2 \dfrac{A}{2}- 3)=-4 \Pi cos \dfrac{A}{2} \Pi (2(cosA+1)- 3)$

$\sum cosA=1+4 \Pi sin \dfrac{A}{2}$


$(1) \leftrightarrow \Pi cos(\dfrac{A}{2}) - \Pi cos \dfrac{A}{2} \Pi (2cosA-1) \ge 8 \Pi (sin \dfrac{A}{2} cos \dfrac{A}{2})$
Chia cả 2 vế cho $\Pi cos(\dfrac{A}{2})$,ta cần chứng minh

$1- \Pi (2cosA-1) \ge 8 \Pi sin\dfrac{A}{2} $
$ \leftrightarrow 1- \Pi (2cosA-1) \ge 2(\sum cosA-1))$

Đến đây,khai triển và nhóm lại ta thu được BĐT quen thuộc hơn

$\Pi (1-cosA) \ge \Pi cosA$


BĐT này có trong nhiều tài liệu.Trường hợp tam giác tù hoặc vuông thì hiển nhiên.Trường hợp tam giác nhọn thì nhân cả 2 về với $\Pi (1+cos A)$
thì BĐT trở thành $\Pi sin^2A \ge \Pi cosA \Pi (1+cosA)$
$\leftrightarrow \Pi sin A \Pi (2sin \dfrac{A}{2} cos \dfrac{A}{2}) \ge \Pi cosA (2cos^2 \dfrac{A}{2})$

$\leftrightarrow \Pi tan A \ge \Pi cot \dfrac{A}{2}$

Áp dụng BĐT Jensen $tan A +tan B \ge 2 tan \dfrac {A+B}{2} =2 cot \dfrac {C}{2} $
viết 2 BĐT tương tự rồi cộng lại ta có điều phải chứng minh.

PS: Bài này chuyển về BĐT đại số với các cạnh của tam giác,chắc cũng được 1 BĐT khó

Đã lột lon sạch sẽ các CTV và BTV sẽ có phương án set lại trong thời gian ngắn tới giờ nghỉ giải lao tí đã ^^

Anh lột cái làm hộp tin nhắn của em bị giảm dung lượng thì phải-> hộp tin nhắn đã đầy,lại phải xóa bao nhiêu tin đi

Bài 5:
Cho 13 điểm phân biệt nằm trong hay trên cạnh của một tam giác đều có cạnh bằng 6 cm.CMR luôn tồn tại hai điểm trong số 13 điểm đã cho mà khoảng cách giữa chúng ko vượt quá $ \sqrt{3} $
Bài này chưa đc xem lời giải đi thi chắc mình bó tay mất

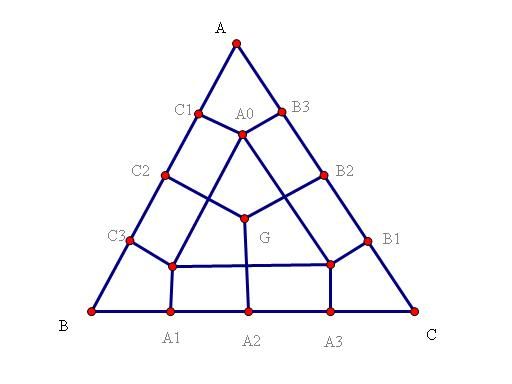
Chia tam giác thành 12 phần như trên.Các điểm $A_1,A_2,A_3$ chia $BC$ thành 4 phần bằng nhau.
$B_1,B_2,B_3$ chia $CA$ thành 4 phần bằng nhau.
$C_1,C_2,C_3$ chia $AB$ thành 4 phần bằng nhau.

$G$ là trọng tâm tam giác.$A_0,B_0,C_0$ lần lượt là trung điểm $GA,GB,GC$

Với 13 điểm luôn tồn tại 2 điểm thuộc cùng 1 phần trong 12 phần trên (nguyên lí Dirichlet)

Dễ tính được các đoạn $GA_0=A_0A=GB_0=B_0B=GC_0=C_0C=\sqrt{3}$
và các đường chéo của các phần hình chữ nhật cũng đề bằng $\sqrt{3}$
Nên với 2 điểm bất kì thuộc cùng 1 phần thì khoảng cách giữa chúng không quá $\sqrt{3}$

Tổng quát với tam giác ban đầu cạnh $a$ thì luôn tồn tại hai điểm trong số 13 điểm đã cho mà khoảng cách giữa chúng không vượt quá $ a\dfrac{\sqrt{3}}{6} $

Ngày 20/11/1997 rơi vào ngày thứ 7. Vậy ngày 20/11/2000 rơi vào ngày thứ mấy? Biết năm 2000 là năm Nhuận
Help meeeeeeeeeeeeeeeee

Trên thực tế thì 20/11/1997 là vào thứ 5 cơ.

Tính số ngày từ 20//11/1997 đến 20/11/2000 ta được 1096 ngày chia 7 dư 4 nên 20/11/2010 sẽ vào thứ 2 (trên thực tế ) và vào thứ tư nếu theo giả thiết bài toán 20/11/1997 rơi vào ngày thứ 7

Hoặc dùng công thức tính một ngày bất kì là thứ mấy ở đây
http://vuthanhtu.tk/website/?p=51

ta có $X=2000$ ,$C=31+29+31+30+31+30+31+31+30+31+20=325$
$ \rightarrow S \rightarrow T=2$

như vậy không cần giả thiết ngày 20/11/1997 rơi vào ngày thứ 7 vẫn tính được