toi tuong=1

$\dpi{200} \small CMR:a\sqrt{\frac{b}{a+c}}+b\sqrt{\frac{c}{a+b}}+c\sqrt{\frac{a}{b+c}}\leq \frac{3\sqrt{3}}{4}\sqrt{\frac{(a+b)(b+c)(c+a)}{a+b+c}}$

hoan toan co the gia su a+b+c=3 hoac abc =1 trong bai nay ma anh

$\dpi{120} \small \;Thuc \;chat \; day \;chinh \; la\;bai \;toan \;: \;Cho \;a,b,c \;la \;cac \;so \;thuc \; duong\; thoa\;man \;a+b+c=3 \;CMR: \frac{a}{b^{3}+2}+\frac{b}{c^{3}+2}+\frac{c}{a^{3}+2}\geq 1\;.Ta CM \; BDT\;nay \; nhu\;sau \;.BDt \; can\;CM \;tuong \;duong \;voi \;(\frac{a}{2}-\frac{a}{b^3+2})+(\frac{b}{2}-\frac{b}{c^3+2})+\left ( \frac{c}{2}-\frac{c}{a^3+2} \right )\leq \frac{1}{2} \;hay \;\frac{ab^3}{b^3+2}+\frac{bc^3}{c^3+2}+\frac{ca^3}{a^3+2}\leq 1 \;Su \;dung \; BDT\;AM-GM \;,ta \;co \;b\leq \frac{b^3+1+1}{3}=\frac{b^3+2}{3}\rightarrow \frac{ab^3}{b^3+2}= \frac{ab^2.b}{b^3+2}\leq \frac{ab^2}{3}\; \rightarrow \sum \frac{ab^3}{b^3+2}\leq\ \frac{ab^2+bc^2+ca^2}{3}\;.Bai \;toan \; quy\; ve\; CM\; ab^2+bc^2+ca^2\leq 3.\;Mat \neq abc=1\rightarrow can CM \; ab^2+bc^2+ca^2+abc\leq 4\;.BDT \;nay \;chinh \; la\; BDT\;co \;ban \;(a+b+c)^3\geq \frac{27}{4}(ab^2+bc^2+ca^2+abc)\rightarrow dpcm \; \; \; \; \; \; \;$

cha hiu sao no ko ra dc latex

$\dpi{150} \small \:Nhan \:2 \: ve\:cua \:Bdt \:cho \:2 \:, \: ta\:can CM \:\frac{a+b}{ab}+\frac{b+c}{bc}+\frac{a+c}{ac}+\frac{2}{\sqrt[3]{abc}}\geq \frac{4(a+b+c+\sqrt[3]{abc})^2}{(a+b)(b+c)(c+a)}. \:Ap \:dung \:Bdt AM-GM, \:ta \:co \:: \:VT=\frac{(a+b)^2}{ab(a+b)}+\frac{(b+c)^2}{bc(b+c)}+\frac{(a+c)^2}{ac(a+c)}+\frac{(2\sqrt[3]{abc})^2}{2abc}\geq \frac{\left [ (a+b+b+c+c+a+2\sqrt[3]{abc}) \right ]^2}{ab(a+b)+bc(b+c)+ca(c+a)+2abc)}=\frac{4(a+b+c+\sqrt[3]{abc})^2}{(a+b)(b+c)(c+a)}= VP\rightarrow dpcm : \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:$

Bài này mình xin trình bày theo cách trâu bò húc $1$ tí

Quy đồng mẫu thức ta có bất đẳng thức tương đương với

       $\frac{\sum (b+c)(c+a}{(a+b)(b+c)(c+a)}+\frac{1}{2\sqrt[3]{abc}}\geqslant \frac{(a+b+c+\sqrt[3]{abc})^2}{(a+b)(b+c)(c+a)}$

$\Leftrightarrow \frac{1}{2\sqrt[3]{abc}}\geqslant \frac{(a+b+c+\sqrt[3]{abc})^2-\sum (b+c)(c+a)}{(a+b)(b+c)(c+a)}$

Khai triển ta được $\Leftrightarrow \frac{1}{2\sqrt[3]{abc}}\geqslant \frac{\sqrt[3]{(abc)^2}+2\sqrt[3]{abc}(a+b+c)-(ab+bc+ca)}{(a+b)(b+c)(c+a)}$

       $\Leftrightarrow (a+b)(b+c)(c+a)\geqslant 2abc+4\sqrt[3]{(abc)^2}(a+b+c)-2\sqrt[3]{abc}(ab+bc+ca)$

       $\Leftrightarrow ab(a+b)+bc(b+c)+ca(c+a)+2\sqrt[3]{abc}(ab+bc+ca)\geqslant 4\sqrt[3]{(abc)^2}(a+b+c)$

D0 bất đẳng thức trên là thuần nhất nên ta có thể chuẩn hóa $abc=1$

Từ đó ta chỉ cần chứng minh bất đẳng thức sau

           $\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}+2(ab+bc+ca)\geqslant 4(a+b+c)$ với $abc=1$

Áp dụng AM-GM ta có $2ab+\frac{a}{b}+\frac{b}{a}=(ab+\frac{a}{b})+(ab+\frac{b}{a})\geqslant 2a+2b=2(a+b)$

                                    $2bc+\frac{b}{c}+\frac{c}{b}\geqslant 2(b+c)$

                                    $2ca+\frac{c}{a}+\frac{a}{c}\geqslant 2(c+a)$

Cộng 3 bđt trên lại ta có đpcm

Đẳng thức xảy ra khi $a=b=c>0$ 

em thu lam cach khac anh xem nhe

Cho $a,b,c$ là các số thực dương. Chứng minh rằng:

 

$\frac{\sqrt{a+b}}{c}+\frac{\sqrt{b+c}}{a}+\frac{\sqrt{c+a}}{b}\geq \frac{4(a+b+c)}{\sqrt{(a+b)(b+c)(c+a)}}$

$\dpi{150} \small $\dpi{150} \small \:Theo \:Bdt \: Holder\: ta\: co\: \sum \sqrt{\frac{b+c}{a}})^2\left [ \sum \frac{1}{a^2(b+c)} \right ]\geq(\sum \frac{1}{}a)^3 \:Do \:đo \:ta \:chi \:can \:CM \ \sum \frac{1}{a})^3\geq \frac{6(a+b+c)}{\sqrt[3]{abc}}\sum \frac{1}{a^2(b+c)}.\:Đặt \:a=\frac{1}{x} ,b= \frac{1}{y},c= \frac{1}{z}\:Bdt\Leftrightarrow \:(x+y+z)^3\geq \6(xy+yz+zx)(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})\:hay \:\frac{(x+y+z)^3}{\sqrt[3]{xyz}} \geq 6(x^2+y^2+z^2)+6xyz(\frac{1}{y+z}+\frac{1}{x+z}+\frac{1}{x+y})\:Áp \dụng \:Bdt Cauchy-Schwarz \: ,\:ta \:có \:6xyz(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y})\leq 6xyz(\frac{1}{4x}+\frac{1}{4y}+\frac{1}{4y}+\frac{1}{4z}+\frac{1}{4z}+\frac{1}{4x})= 3(xy+yz+zx)\:\frac{(x+y+z)^4}{\sqrt[3]{xyz}}\geq \3(x+y+z)^3. \:Như \:vậy \:ta \:chỉ \:cần \:CM \::3(x+y+z)^3\geq 6(x^2+y^2+z^2)+3(xy+yz+zx).Sau khi thu gọn ta dc dpcm.Đay \:là \:cách \: làm\:của \:em \moi : \:nguoi\:xem \:ho \:em \:nhe \: \: \: \: \: \: \: \: \: \:$$

$\dpi{150} \small \:hinh \:nhu \:la \:nam \:1766 \:dung \:ko \: a\: \: \:$

a u toi nham ti toi sua

$\dpi{150} \small Bai nay thuc chat la bai toan co ban sau (a+b+c)^3\geq \frac{27}{4}(ab^2+bc^2+ca^2+abc)$

$\dpi{150} \small \:Theo \:Bdt \: Holder\: ta\: co\: \sum \sqrt{\frac{b+c}{a}})^2\left [ \sum \frac{1}{a^2(b+c)} \right ]\geq(\sum \frac{1}{}a)^3 \:Do \:đo \:ta \:chi \:can \:CM \ \sum \frac{1}{a})^3\geq \frac{6(a+b+c)}{\sqrt[3]{abc}}\sum \frac{1}{a^2(b+c)}.\:Đặt \:a=\frac{1}{x} ,b= \frac{1}{y},c= \frac{1}{z}\:Bdt\Leftrightarrow \:(x+y+z)^3\geq \6(xy+yz+zx)(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})\:hay \:\frac{(x+y+z)^3}{\sqrt[3]{xyz}} \geq 6(x^2+y^2+z^2)+6xyz(\frac{1}{y+z}+\frac{1}{x+z}+\frac{1}{x+y})\:Áp \dụng \:Bdt Cauchy-Schwarz \: ,\:ta \:có \:6xyz(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y})\leq 6xyz(\frac{1}{4x}+\frac{1}{4y}+\frac{1}{4y}+\frac{1}{4z}+\frac{1}{4z}+\frac{1}{4x})= 3(xy+yz+zx)\:\frac{(x+y+z)^4}{\sqrt[3]{xyz}}\geq \3(x+y+z)^3. \:Như \:vậy \:ta \:chỉ \:cần \:CM \::3(x+y+z)^3\geq 6(x^2+y^2+z^2)+3(xy+yz+zx).Sau khi thu gọn ta dc dpcm.Đay \:là \:cách \: làm\:của \:em \moi : \:nguoi\:xem \:ho \:em \:nhe \: \: \: \: \: \: \: \: \: \:$

$\dpi{150} \small \:Dat \:b _{n}=\frac{1}{u_{n}}\rightarrow \:b_{1}=2 \:va \: b_{n+1}=b_{n}^2-b_{n}+1\rightarrow \frac{1}{b_{n+1}-1}=\frac{1}{b_{n}(b_{n}-1)}=\frac{1}{b_{n}}-\frac{1}{b_{n}-1}\rightarrow \frac{1}{b_{n}}=\frac{1}{b_{n-1}}-\frac{1}{b_{n+1}-1}\ \:Ta \:có \::\sum_{i=1}^{n} u_{i}=u1+u2+...+un=\frac{1}{b_{1}}+\frac{1}{b_{2}}+.....+\frac{1}{b_{n}}= \frac{1}{b_{1}-1}-\frac{1}{b_{2}-1}+\frac{1}{b_{2}-1}-\frac{1}{b_{3}-1}+.....+\frac{1}{b_{n}-1}-\frac{1}{b_{n+1}-1}=\frac{1}{b_{1}-1}-\frac{1}{b_{n+1-1}}=\frac{1}{2-1}-\frac{1}{b_{n+1}-1}< 1\rightarrow dpcm\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:$

$\dpi{150} \small Áp\: dung\:bdt \:Cauchy \:cho \:3 \:số \:ko \:âm \:a,b,c. \:Ta có: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:ab^2=a.b.b\leq \frac{a^3+2b^3}{3} \:Tg \:tu, \:ta \:cung co \: bc^2\leq \frac{b^3+2c^3}{3},\:ca^2\leq \frac{c^2+2a^2}{3} \rightarrow ab^2+bc^2+ca^2\leq a^3+b^3+c^3.Áp dụng BDt Holder cho 3 so ta có:9(a^3+b^3+c^3)=(1^3+1^3+1^3)(a^3+b^3+c^3)(1^3+1^3+1^3)\geq (1.1.a+1.1.b+1.1.c)^3\rightarrow 9(a^3+b^3+c^3)\geq (a+b+c)^3,lai có abc\leq \frac{(a+b+c)^3}{27\rightarrow }\:ab^2+bc^2+ca^2+abc\leq a^3+b^3+c^3+abc\leq \frac{(a+b+c)^3}{9}+\frac{(a+b+c)^3}{27}=4\rightarrow dpcm \: \: \: \: \: \: \:$

$\dpi{150} \small \:AB=2a\:\rightarrow AH=a. \: Ta\:có \:\OH^2=R^2-a^2\rightarrow \:OH=\sqrt{R^2-a^2}\rightarrow HE=OE-OH=R-\sqrt{R^2-a^2} \:Ta \: có\:AE^2=AH^2+HE^2=a^2+(R-\sqrt{R^2-a^2})^2=2R^2-2R\sqrt{R^2- a^2}+a^2=R^2-2R\sqrt{R^2-a^2}+R^2-a^2+2a^2=(R-\sqrt{R^2-a^2})^2+2a^2 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:$

$\dpi{150} \small Bài\, hinh \, cau 3\,minh \,giải \, thế này \, các \, bạn \,xem hộ \,mình \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,Lấy \, G\,là \,tâm \,đường \,tròn \,ngoại \,tiêp \,\Delta A1B1C1 \,giả \,sử \,G \,nằm \,trên \,cung AB .\,Lấy \,M \,là \,điểm \,chính \,giữa \,cung AC \,\rightarrow MA=MC,AC1=CA1, \,lại \,có \,MACB là tứ \,giác \,nội \,tiếp\rightarrow \,\angle MAC1= \angle MCA1\rightarrow \Delta MC1A=\Delta MA1C\rightarrow MC1=MA1\rightarrow G\equiv M \, (\Delta A1B1C1)\cap BC\,tại X \,\Delta GXB va\Delta GC1B \,có \,GX=GC1 ,\,GB \,là \,cạnh \,chung \, Tứ\, giác\,GACB nt \rightarrow \,\angle GBX=\angle GAC=\angle GCA= \angle GBA \,\rightarrow \Delta GBA=\Delta GBX\rightarrow BX=BC1=s-a \,ta \, cũng\,có \,CA1=s-b \,va CX=CA=s \,.Tương\,tự \,(A1B1C1) \cap AC\,la \,Y \, ta \,cũng \,có \,AB1=CY=s-c \,và \,CB1=s-a. \,Theo \,tc \,phương \,tích \,ta \,có \,CA1. CX=CY.CB1\rightarrow s(s-b)=(s-a)(s-c) \rightarrow a^2=b^2+c^2\rightarrow dpcm\, \, \, \, \, \, \, \,$

gần nhất bạn ạ, vì mình xét hai nửa mặt phẳng cơ mà

minh nham thong cam nhe

$\dpi{150} \small Ta co:x^6+y^4\geq 2\sqrt{x^6y^4}=2x^3y^2\rightarrow \frac{2x}{x^6+y^4}\leq \frac{1}{x^2y^2}\rightarrow \sum \frac{1}{x^2y^2}\geq \sum \frac{2x^6}{x^6+y^4}.Lai co \sum \frac{1}{x^2y^2}\leq \sum \frac{1}{x^4}(BDT Co si)\rightarrow dpcm$

Nguyênta98 oi phai la điểm Y ở xa AB nhất chứ,thế mới thỏa mãn


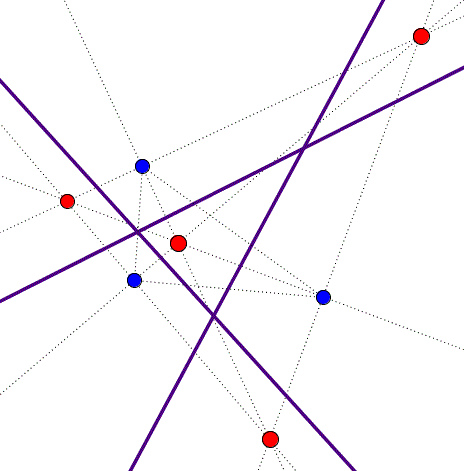
$\dpi{150}$ Giả sử ta có 2a +1 điểm màu đỏ và màu xanh điểm b, trong đó 2a+ 1 \leq b. Sau đó bởi trên SCP đối số, số lượng cần thiết của đường đến các điểm riêng biệt là 2a+ 1. Ngoài ra, rõ ràng là đủ số lượng dòng là 2a +2, bởi vì ta luôn luôn có thể sử dụng 1 cặp đường đến các điểm riêng biệt theo từng cặp. Từ vấn đề, chúng ta có thể kết luận rằng cho b = 2a +1 hoặc b = 2a+ 2, số lượng đầy đủ của dòng là 2a+ 1. Tuy nhiên, nó không phải là trường hợp đó cho mỗi b, số lượng đủ là 2a +1. Ví dụ, giả sử a = 1, b = 7. Ta có 2a +1 = 3 điểm màu đỏ và giả sử chúng ta đặt 7 điểm còn lại trong bảy khu vực khác nhau xác định bởi tam giác màu đỏ. Sau đó có ba dòng sẽ không đủ để điểm riêng biệt. Phần còn lại ai giúp mình với

cau 9:d

1A:21,2C:21,27,                                                                                                                                                                                                                                           8D: vi theo thu tu nho dan đi                                                                                                                                                                                                                          

minh nghi la bang 4

$\dpi{150} \small Khong mat tinh tong quat gia su a\leq b\leq c.Ta cóp^2=(a^2+b^2+c^2)^2\rightarrow \left [(a^4+b^4+c^4)+2(a^2b^2+b^2c^2+a^2c^2) \right ]\vdots p.Ma (a^4+b^4+c^4)\vdots p\rightarrow 2(a^2b^2+b^2c^2+a^2c^2)\vdots p.Mat\neq a,b,c\geq 1\rightarrow p\geq 3\rightarrow (p,2)=1\rightarrow (a^2b^2+b^2c^2+a^2c^2)\vdots p .Do đó \left [ a^2b^2+c^2(a^2+b^2+c^2)-c^4 \right ]\vdots p\rightarrow a^2b^2-c^4\vdots p\Leftrightarrow (ab-c^2)(ab+c^2)\vdots p.Lai có ab< 2ab\leq a^2+b^2\rightarrow 1< ab+c^2< a^2+b^2+c^2=p\rightarrow (ab+c^2,p)=1\rightarrow ab-c^2\vdots p.Mat\neq 1\leq a\leq b\leq c\rightarrow 0\leq c^2-ab< c^2< a^2+b^2+c^2=p\rightarrow c^2-ab=0\rightarrow c^2=ab\rightarrow p=3a^2.Ma p la số nguyên tố\rightarrow a=1\rightarrow p=3$

$\dpi{150} \small b) Theo cau a ta co:BI la phan giac \angle B\rightarrow I la tam duong tron noi tiep \Delta ABC\rightarrow AI di qua diem chinh gia cung BC cố dinh\rightarrow dpcm$