Ai giúp mình câu 5 với ?

hôm nay mới có thời gian vào diễn đàn

cảm ơn bạn

 Có bạn nào có cuốn "Hình học tổ hợp" của Phan Huy Khải không?

Nếu có thì up lên cho mình với. 

Có ai làm bài hình chưa? Chỉ cho mình với

Cho tam giác ABC nhọn, đường cao AD, BE, CF. Gọi (X), (Y), (Z) là các đường tròn nội tiếp tam giác AEF, BFD, CDE. Gọi d_a là tiếp tuyến chung ngoài khác BC của (Y), (Z) .Tương tự ta có d_b, d_c. Chứng minh  d_a, d_b, d_c đồng quy.

Cho các số nguyên dương a, b, c, d sao cho $(ac+bd) \vdots (a^2+b^2)$.  Chứng minh $(a^2+b^2, c^2+d^2)>1$ 

Bài 6 (Trường LHP): Cho D là điểm trên cạnh BC của tam giác ABC sao cho $\angle$CAD=$\angle$CBA. Một đường tròn tâm O đi qua B và D lần lượt cắt AB, AD tại E, F. Đường thẳng BF và DE cắt nhau tại G. M là trung điểm AG. Chứng minh CM vuông góc với AO.

Bổ đề: Cho tứ giác ABCD nội tiếp đường tròn tâm O. AD cắt BC tại Q. AB cắt CD tại P. AC cắt BD tại I. Khi đó O là trực tâm tam giác IPQ.

Trở lại bài toán ban đầu:

Gọi H=EF$\cap$BC, K=EF$\cap$AG, J=AG$\cap$BC.

Ta có: $\angle$EFA=$\angle$ABD$\Rightarrow$$\angle$EFA=$\angle$DAC$\Rightarrow$EF//AC

Áp dụng bổ đề ta có O là trực tâm tam giác AGH $\Rightarrow$ HG vuông góc AO. Ta cần C/m CM//HG.

AJ, BF, DE đồng quy, H=EF $\cap$BC $\Rightarrow$(BDJH)=-1

$\Rightarrow$(AGJK)=-1(Phép chiếu xuyên tâm E).

Mà M là trung điểm AG nên 

$\overline{JG}$.$\overline{JA}$=$\overline{JK}$.$\overline{JM}$(Hệ thức Maclaurin)$\Rightarrow$JG.JA=JK.JM

$\Rightarrow$$\frac{JA}{JK}$=$\frac{JM}{JG}$

Lại có $\frac{JA}{JK}$=$\frac{JC}{JH}$ (do EF//HG) nên $\frac{JM}{JG}$=$\frac{JC}{JH}$$\Rightarrow$GH//MC$\Rightarrow$đpcm

Phép chiếu xuyên tâm bảo toàn tỉ số kép đó bạn. Cái này mình đọc trong Tài liệu chuyên toán 10 Hình.

Ở đây là phép chiếu xuyên tâm E, đi từ đường thẳng BC đến đường thẳng AG.

Bài 3. Cho tam giác $ABC$ nhọn khác tam giác cân nội tiếp đường tròn $\omega$. Gọi $D,E,F$ lần lượt là tâm đường tròn bàng tiếp tương ứng với đỉnh $A,B,C$ là $I$ là tâm đường tròn nội tiếp tam giác $ABC$. Đường tròn ngoại tiếp tam giác $EFI$ cắt $\omega$ tại $A_{1},A_{2}$.

$a)$ Chứng minh các đường thẳng $A_{1}A_{2}, EF, BC$ đồng quy.

$b)$ Đường tròn ngoại tiếp tam giác $DIF$ cắt $\omega$ tại $B_{1},B_{2}$; đường tròn ngoại tiếp tam giác $DIE$ cắt $\omega$ tại $C_{1},C_{2}$. Các đường thẳng $A_{1}A_{2}, B_{1}B_{2}, C_{1}C_{2}$ đôi một cắt nhau tạo thành một tam giác, chứng minh rằng diện tích tam giác nhỏ hơn $\frac{1}{4}$ diện tích tam giác $ABC$.

a) Bằng các biến đổi góc, ta dễ có $\widehat{BFE}$+$\widehat{BCE}$=180$^{\circ}$$\Rightarrow$BCEF nội tiếp.

    Ta có BCEF nội tiếp, BA₁A₂C nội tiếp, FA₁A₂E nội tiếp $\Rightarrow$ BC là trục đẳng phương của $\omega$ và (BCE), 

    A₁A₂ lá trục đẳng phương của $\omega$ và (FIE), EF là trục đẳng phương của (BCE) và (FIE)

    Suy ra BC, EF, A₁A₂ đồng quy.

b) Dễ thấy FAIB nội tiếp.

    Ta có AB là trục đẳng phương của $\omega$ và (FAB), IF là trục đẳng phương của (FIE) và (FAB),     A     ₁A₂ là trục đẳng phương của $\omega$ và (FIE) $\Rightarrow$ AB, A  ₁A₂, FI  đồng quy (1).

    Ta có B₁B₂ là trục đẳng phương của $\omega$ và (FID), IF là trục đẳng phương của (FIE) và (FID),     A     ₁A₂  là trục đẳng phương của $\omega$ và (FIE) $\Rightarrow$ B ₁B₂, A₁A₂, IF đồng quy (2).

    Từ (1) và (2) suy ra    B₁B₂, A₁A₂, IF, AB đồng quy  $\Rightarrow$ Giao điểm của A  ₁A₂ và B₁B₂ là chân đường phân giác từ

    đỉnh C của $\Delta$ABC.

    Tương tự đối với A₁A₂ và C₁C_2,  C₁C₂ và B₁B₂.

    Vậy tam giác tạo bởi 3 đường thẳng   A ₁A₂, B₁B₂, C₁C₂ là tam giác tạo bởi chân 3 đường phân giác trong $\Delta$ABC.

    Gọi các chân đường phân giác là M, N, P.

    Ta có :$\frac{S_BMP}{S_ABC}$=$\frac{BM.BP}{BC.BA}$=$\frac{c}{b+c}$.$\frac{a}{a+b}$$\frac{ac}{(a+b)(b+c)}$

    Tương tự: $\frac{S_APN}{S_ABC}$=$\frac{bc}{(a+b)(c+a)}$, $\frac{S_CMN}{S_ABC}$=$\frac{ab}{(b+c)(c+a)}$

  Vậy :$\frac{S_BPM}{S_ABC}$+$\frac{S_APN}{S_ABC}$+$\frac{S_CMN}{S_ABC}$ = $\frac{$\sum$ab(a+b)}{(a+b)(b+c)(c+a)}$=T

  Ta có: T=$\frac{(a+b)(b+c)(c+a)-2abc}{(a+b)(b+c)(c+a)}$

               $\geqslant$$\frac{(a+b)(b+c)(c+a)-(a+b)(b+c)(c+a)/4}{(a+b)(b+c)(c+a)}$=3/4

  Ta có: $\frac{S_MNP}{S_ABC}$=1-T$\leqslant$1-$\frac{3}{4}$=$\frac{1}{4}$

   Dấu "=" không xảy ra do tam giác ABC không đều $\Rightarrow$ đpcm

Bài toán này chỉ cần A, B thuộc cùng một nửa mặt phẳng bờ d.

Gọi A' là điểm đối xứng của A qua đường thẳng d, suy ra A' cố định

Với mọi điểm M thuộc d thì MA'=MA. Ta có: MA+MB=MA'+MB$\geq$A'B không đổi.

Vậy MA+MB nhỏ nhất khi và chỉ khi M là giao điểm của A'B và đường thẳng d (với A' xác định như trên).

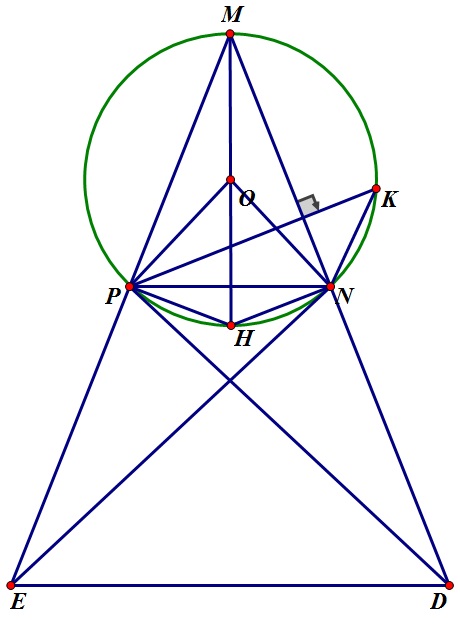
a) Vì NE và PD là tiếp tuyến của (O) nên $\widehat{PNE}$=$\widehat{NPD}$=$\widehat{PMN}$.  

Lại có $\widehat{NPE}$=$\widehat{PND}$ $\Rightarrow$ $\widehat{DPE}$=$\widehat{END}$ 

$\Rightarrow$ PNDE nội tiếp.

b) Kẻ đường kính MH của (O), suy ra NH vuông góc với MN $\Rightarrow$ NH//PK

$\Rightarrow$ PH=NK.

Vậy MN²+NK²=MP²+PH²=MH²=4R².

Gọi M, P lần lượt là hinh chiếu của O lên AC, AB. N là hình ciếu của M lên AB.

Khi đó, dễ thấy d₂ vuông góc với MD, d₃ vuông góc với OM.

Xem BC là một trục. Giả sử D(0), A(a), E(x).

Khi đó B(-a), N($\frac{a}{2}$), P($\frac{a+x}{2}$).

Ta có:  (DO²-DD²)+(ED²-EM²)+(BM²-BO²)

          =(DO²-BO²)+(BM²-EM²)+ED²

          =(DP²-BP²)+(BN²-EN²)+ED²

         =($\frac{a+x}{2}$-0)²-($\frac{a+x}{2}$-(-a))²+($\frac{a}{2}$-(-a))²-($\frac{a}{2}$-x)²+(0-x)²=0.

Áp dụng định lý Carnot cho tam giác OMD suy ra d₁, d₂, d₃ đồng quy

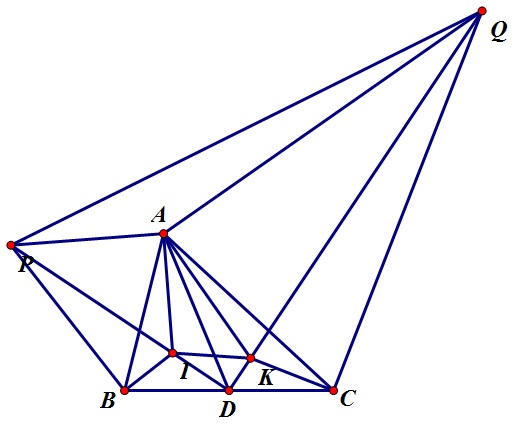
Dễ có $\widehat{PBI}$=$\widehat{PAI}$=90^o nên PAIB nội tiếp. Suy ra $\widehat{APD}$=$\widehat{ABI}$

$\Rightarrow$$\widehat{APD}$=$\widehat{IBD}$.

Ta có $\widehat{APD}$=$\widehat{IBD}$, $\widehat{PDA}$=$\widehat{IDB}$

$\Rightarrow$ tam giác ADP đồng dạng với tam giác IDB

$\Rightarrow$$\frac{AD}{DP}$=$\frac{ID}{DB}$$\Rightarrow$DI.DP=DA.DB (1).

Tương tự, ta có DK.DQ=DA.DC (2).

D là trung điểm BC nên DB=DC (3).

Từ (1), (2), (3) suy ra DI.DP=DK.DQ$\Rightarrow$IKQP nội tiếp$\Rightarrow$đpcm

Cho a, b, c > 0 và a²+b²+c²+2abc=1.

Chứng minh a²+b²+c²$\geq$4(a²b²+b²c²+c²a²)

Gọi J là trung điểm AC.

Đặt $\widehat{ABJ}$=$\alpha$, $\widehat{CBJ}$=$\beta$.

Dễ có: AB.sin($\alpha$)=BC.sin($\beta$).

Ta sẽ chứng minh BJ vuông góc với DK.

Ta có: BJ vuông góc với DK $\Leftrightarrow$ BD²-BK²=JD²-JK²

$\Leftrightarrow$ BD²-BK²=(JB²+BD²-2JB.BD.cos($\widehat{JBD}$))-(JB²+BK²-2JB.BK.cos($\widehat{JBK}$))

$\Leftrightarrow$ BD.cos($\widehat{JBD}$)=BK.cos($\widehat{JBK}$)  $\Leftrightarrow$BD.cos($\pi$+$\alpha$)=BK.cos($\pi$+$\beta$)  $\Leftrightarrow$AB.sin($\alpha$)=BC.sin($\beta$) (đúng).

Vậy các đường cao của tam giác AGE, BDK, CIF lần lượt đi qua trung điểm của BC, CA, AB

Suy ra chúng đồng quy $\Rightarrow$ đpcm.

Cho các số thực dương a, b, c và a+b+c$\leq$3.

Chứng minh $\Sigma$$\sqrt{a}$$\geq$$\Sigma$ab

Áp dụng tính chất của tứ giác điều hòa và định lý Ptôlêmê vào các tứ giác nội tiếp và điều hòa nói trên,

ta được: AC.BD=2AB.CD (1)

              AF.DE=$\frac{1}{2}$AE.DF (2)

              BD.AF=AB.DF (3)

Từ (1), (2), (3) suy ra AC.DE=AE.CD $\Rightarrow$ ACDE là tứ giác điều hòa.

Chứng minh thế này nè em.

Gọi M, N là hình chiếu của B, J lên DK.

Khi đó, BJ vuông góc với DK$\Leftrightarrow$M$\equiv$N$\Leftrightarrow$MD²-MK²=ND²-NK²

$\Leftrightarrow$BD²-BK²=JD²-JK².

Cái này cũng là một cách thường dùng, được sử dụng luôn đó.

Sao khủng quá vậy. Con đường đi tới như thế nào vậy bạn ?

Sử dụng bổ đề rồi làm sao nữa vậy ?

Cho $\vartriangle ABC$ có đường cao $AD,BE,CF$ đồng quy tại $H$.

Gọi $O;O_a;O_b;O_c$ thứ tự là tâm đường tròn ngoại tiếp các tam giác $ABC,AEF,DBF,DEC$.

Gọi $X,X_a,X_b,X_c$ thứ tự có cùng tọa độ tỉ cự đối với các tam giác $ABC,AEF,DBF,DEC$ sao cho $X \ne O;X_a \ne O_a; X_b \ne O_b; X_c \ne O_c$.

Chứng minh rằng: $X_aO_a;X_bO_b;X_cO_c$ đồng quy

 

Spoiler

Khá dễ

Mình không hiều đề lắm. "tọa độ tỉ cự" là gì vậy ?

Bạn giải cụ thể luôn được không ?

Do a, b, c > 0 và abc=1 nên tồn tại các số thực dương x, y, z sao cho  

a=$\frac{x}{y}$, b=$\frac{y}{z}$, c=$\frac{z}{x}$.

Cần chứng minh $\sum \frac{1}{\frac{2x}{y}+1}$ $\geq$ 1 .

Ta có: $\sum \frac{1}{\frac{2x}{y}+1}$=$\sum \frac{x}{2z+x}$=$\sum \frac{x^2}{2xz+x^2}$ $\geq$ $\frac{(x+y+z)^2}{x^2+y^2+z^2+2xy+2yz+2zx}$=1.

Vậy thì sẽ là $a\to 0, b=c\to \dfrac{\sqrt{2}}{2}$ và các hoán vị.

Dấu mũi tên nghĩa là sao vậy bạn ?

Hình như nhầm rồi Tùng. Phải chứng minh (c-ka) và (d-kb) đều không âm đã. Mà nếu tiếp tục thì làm sao có k=1 được. Chỗ kia là d=kb mà, mày ghi là b=kb