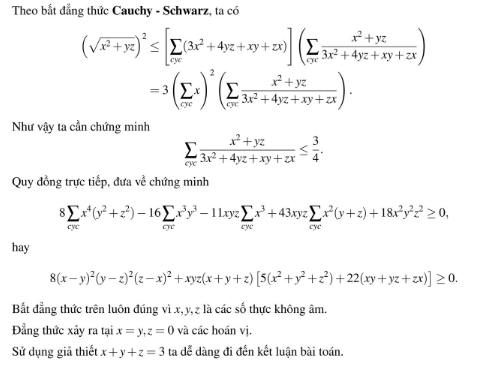huytran08

cơ mà đoạn này với x = y = 3/2  và z = 0 thì dấu = có xảy ra đâu 

bqt cho em hỏi tại sao khi gõ latex thì em không đăng bài được ạ

À đấy là mình ghi dấu "=" bất kì nên thế

Khi dùng $LaTeX$ thì bạn phải kẹp công thức toán trong dấu $ .Ví dụ x^{2}+y^{2}=5 khi kẹp thành $x^{2}+y^{2}=5$

B có cách nào khác k

Còn 1 cách nha bạn:

Bài khó thật,mần mãi mới ra:

  Không mất tính tổng quát giả sử $z=$max{$x,y,z$} 

+Nếu $z=3$ thì $x=y=0$ suy ra $T=3$

+Nếu $z<3$

Theo $AM-GM$ ta có:$ \sqrt{x^{2}+yz}\leq \frac{1}{2}\left ( \frac{x^{2}+yz}{x+y}+x+y \right )=\frac{2x^{2}+y^{2}+2xy+yz}{2(x+y)}$

                                     

                                     $\sqrt{y^{2}+xz}\leq \frac{1}{2}\left ( \frac{y^{2}+xz}{x+y}+x+y \right )=\frac{x^{2}+2y^{2}+2xy+xz}{2(x+y)}$

 

Mặt khác:$ \sqrt{z^{2}+xy}=\sqrt{\left ( z+\frac{xy}{x+y} \right )^{2}-\left ( \frac{xy}{x+y} \right )^{2}-\frac{xy(2z-x-y)}{x+y}}\leq z+\frac{xy}{x+y}=\frac{2(xy+yz+xz)}{2(x+y)}$

 

Cộng lại ta có:$ T=\sum \sqrt{x^{2}+yz}\leq \frac{3x^{2}+3y^{2}+6xy+3yz+3xz}{2(x+y)}=\frac{3(x+y+z)}{2}=\frac{9}{2}$

  Dấu "=" xảy ra $\Leftrightarrow x=y=\frac{3}{2},z=0$ và các hoán vị

  P/s:Bài này có tìm được Min không nhỉ?

Ta sẽ chứng minh:$ \sum \frac{ab}{a+b}\leq \frac{3}{2}.\frac{ab+bc+ac}{a+b+c}$

 Thật vậy:$\sum \frac{ab}{a+b}\leq \frac{3}{2}.\frac{ab+bc+ac}{a+b+c}\Leftrightarrow (a+b+c)\left ( \sum \frac{ab}{a+b} \right )\leq \frac{3}{2}(ab+bc+ac)$

               $\Leftrightarrow \sum \frac{1}{a+b}\leq \frac{1}{2}\left ( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )$ (luôn đúng)

         $ \Rightarrow \sum \frac{ab}{a+b}\leq \frac{3}{2}.\frac{ab+bc+ac}{a+b+c}\leq \frac{3}{2}$

 Dấu "=" xảy ra $\Leftrightarrow a=b=c=1$ (thỏa mãn)

Ta có:$ \sqrt{a^{3}+b^{2}+2c}\geq \sqrt{a^{3}+2(b+c)-1}=\sqrt{a^{3}-2a+5}$

 Xét:$ \sqrt{a^{3}-2a+5}\geq \frac{a+7}{4}\Leftrightarrow (a-1)^{2}(16a+31)\geq 0$ (luôn đúng $\forall a\geq 0$)

              $\Rightarrow \sqrt{a^{3}+b^{2}+2c}\geq \frac{a+7}{4}$ 

 

Tương tự cộng lại ta có:$ \Rightarrow \sum \sqrt{a^{3}+b^{2}+2c}\geq 6$

 Dấu "=" xảy ra $\Leftrightarrow a=b=c=1$ ( thoả mãn)

Giả sử $a,b,m$ là các số nguyên,$m> 0$ và $(a,m)=d$.Chứng minh rằng:

a,Nếu $b$ không chia hết cho $d$ thì đồng dư $ax\equiv b \pmod{m}$ vô nghiệm.

b,Nếu $d\mid b$ thì $ax\equiv b \pmod{m}$ có đúng $d$ nghiệm không đồng dư mod $m$.

Mình giải câu 2.2 như thế này,không biết có sai không   :

Đặt $x=a^{2}+b^{2}+c^{2},y=ab+bc+ac$ thì $x\geq y$ và BĐT cần chứng minh trở thành:

                                         $\sqrt{x+2y}\geq \frac{4x}{y}+5$

Ta có:$y=abc \leq \sqrt{\frac{y^{3}}{27}}\Rightarrow y\geq 27\Rightarrow x\geq 27$

 Suy ra $\sqrt{x+2y}\geq \sqrt{x+54}$ và $\frac{4x}{y}+5\leq \frac{4x}{27}+5$

  Tức là ta cần chứng minh:$ \sqrt{x+54}\geq \frac{4x}{27}+5$

 Thật vậy: $\sqrt{x+54}\geq \frac{4x}{27}+5\Leftrightarrow (x-27)(16x+783)\leq 0 $(luôn đúng $\forall x\geq 27$)

              $\Rightarrow a+b+c\geq 4\left ( \frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab} \right )+5$

 Dấu "=" xảy ra $\Leftrightarrow a=b=c=3$(thỏa mãn)

7-8 điểm bạn ạ

Đề này bạn làm được tầm mấy điểm thế

Đề toán KHTN vòng 2,mời các cao nhân làm c hình hộ ạ.

Cho tam giác $ABC$ nhọn,không cân có trọng tâm $G$,tâm ngoại tiếp $O$.Gọi $D,E,F$ lần lượt là tâm ngoại tiếp các tam giác $GBC,GCA,GAB$.Chứng minh rằng $O$ là trọng tâm tam giác $DEF$.

Bunhia với cauchy schwarz là 1 mà

Bài này có lẽ tổng quát được như sau 

 

Bài toán. Chứng minh $2^{3^n}+1$ chia hết cho $3^{n+1}$ nhưng không chia hết cho $3^{n+2}$. 

 

Chưa chứng minh được, nhưng thử vài trường hợp đầu tiên của $n$ thấy đúng. 

 

$2^{3^0}+1=3$ chia hết cho $3^{0+1}=3$ nhưng không chia hết cho $3^{0+2}=9$.

$2^{3^1}+1=9$ chia hết cho $3^{1+1}=9$ nhưng không chia hết cho $3^{1+2}=27$. 

$2^{3^2}+1=513$ chia hết cho $3^{2+1}=27$ nhưng không chia hết cho $3^{2+2}=81$. 

$2^{3^3}+1=134217729$ chia hết cho $3^{3+1}=81$ nhưng không chia hết cho $3^{3+2}=243$. 

 

Quy nạp được chăng? 

Bài này dùng quy nạp thật:

Tạm gọi đpcm là (1)

Xét với $n=1$ thoả mãn

Giả sử (1) đúng với $n=k$,ta chứng minh (1) cũng đúng với $n=k+1$

Thật vậy: $2^{3^{k+1}}+1=8^{3^{k}}+1=(2^{3^{k}}+1)(4^{3^{k}}-2^{3^{k}}+1)$

 Mà $2^{3^{k}}+1\vdots 3^{k+1};4^{3^{k}}-2^{3^{k}}+1=4^{3^{k}}+2-(2^{3^{k}}+1)\vdots 3$ nên  $2^{3^{k+1}}+1 \vdots 3^{k+2}$

  Như vậy ta chỉ cần chứng minh $2^{3^{k+1}}+1$ không chia hết cho $3^{k+3}$ hay $4^{3^{k}}-2^{3^{k}}+1$ không chia hết cho $9$ 

Ta có: $4^{3^{k}}-2^{3^{k}}+1= (2^{3^{k}}+1)^{2}-3.2^{3^{k}}$ không chia hết cho $9$

  Suy ra $2^{3^{k+1}}+1$ không chia hết cho $3^{k+3}$

 Từ các chứng minh trên ta có đpcm.

Bài này là bài thi KT kiến thức toán 9 trường KHTN đợt 4 vòng 1 thì phải:

  Áp dụng BĐT $Cauchy-Schwarz$ ta có:

           $P^{2}\leq 7(xy+yz+xz)\left ( \frac{x}{3x+4z}+\frac{y}{3y+4x}+\frac{z}{3z+4y} \right )$(1)

 Đặt $a=x^{2}+y^{2}+z^{2},b=xy+yz+xz$ thì $b\leq \frac{1}{3}$

 Xét:$ \frac{4z}{3x+4z}+\frac{4x}{3y+4x}+\frac{4y}{3z+4y}+\frac{3}{7(xy+yz+xz)}$

   $ = \frac{4z^{2}}{3xz+4z^{2}}+\frac{4x^{2}}{3xy+4x^{2}}+\frac{4y^{2}}{3yz+4y^{2}}+\frac{3}{7(xy+yz+xz)}\geq \frac{4}{3(xy+yz+xz)+4(x^{2}+y^{2}+z^{2})}+\frac{3}{7(xy+yz+xz)}$

                                                                                $= \frac{4}{3b+4a}+\frac{3}{7b}$

                                                                                $= \frac{16}{4(3b+4a)}+\frac{9}{21b} \geq \frac{49}{16a+33b}=\frac{49}{16+b}\geq 3$

    $\Rightarrow \frac{x}{3x+4z}+\frac{y}{3y+4x}+\frac{z}{3z+4y}\leq \frac{1}{ 7(xy+yz+xz)}$(2)

  Từ (1) và (2) $\Rightarrow P\leq 1$

   Dấu "$=$" xảy ra $\Leftrightarrow x=y=z=\frac{1}{3}$(thoả mãn)

 

Thực ra cái này rất đơn giản. Tạm gọi đpcm là (1).

Xét thấy $n=0$ và $n=1$ thoả mãn.

Giả sử (1) đúng với $n=k$, ta chứng minh (1) cũng đúng với $n=k+1$.

Thật vậy $ \cos\left ( \frac{90^{o}}{2^{k}} \right )=\cos\left ( 2.\frac{90^{o}}{2^{k+1}} \right )=2.\cos^{2}\left ( \frac{90^{o}}{2^{k+1}} \right )-1$

              $\Rightarrow \cos\left ( \frac{90^{o}}{2^{k+1}} \right )=\frac{\sqrt{2+\cos\left ( \frac{90^{o}}{2^{k}} \right )}}{2}=\frac{\sqrt{2+\sqrt{2+\sqrt{2+...}}}}{2}$ (có $k+1$ dấu căn).

Từ các chứng minh trên ta có đpcm.