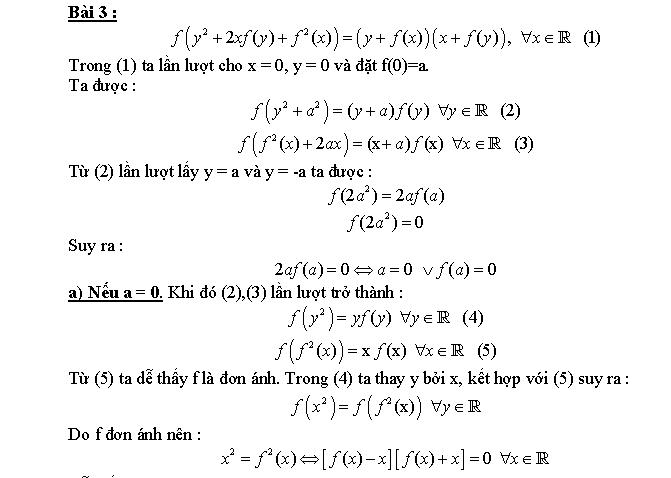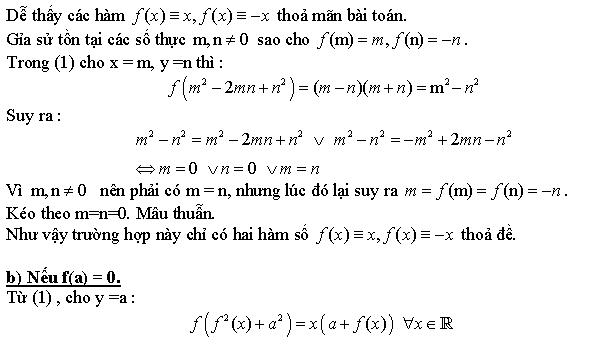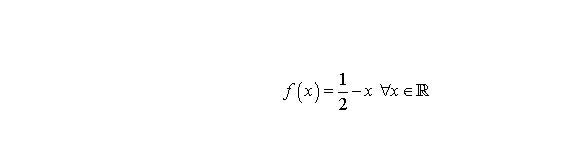Trong một hộp có 10 tấm thẻ được đánh số 0,1,2,..,9. Lấy ngẫu nhiên bốn thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải. Hỏi có bao nhiêu cách xếp để bốn thẻ xếp thành một số tự nhiên chẵn.

Cho các số thực $x,y>1$. Tìm giá trị nhỏ nhất :

$$P=\dfrac{1}{x-1}+\dfrac{1}{y-1}+\dfrac{4}{x^2+y^2}+5\sqrt{x+y}$$

Bài toán (Chọn đội dự tuyển Đồng Nai 2015-2016)

Tìm tất cả các số nguyên dương $n$ sao cho $(n^2+11n-4)n!+33.13^n+4$ là số chính phương.

Giải hệ phương trình gồm hai phương trình sau :
$$x^3-3x+2=2y^3-y^2$$
$$\sqrt{2x-y-1}+\sqrt{3y+1}=\sqrt{x+y}+\sqrt{x}$$

 Bài toán: Cho các số thực dương $a,b,c$. CMR:

 

    $(\frac{a}{a+b})^2+(\frac{b}{b+c})^2+(\frac{c}{c+a})^2+3\geq \frac{5}{2}(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a})$

 

 

Lời giải của mình như thế này :

 

Đặt $x=\frac{a}{a+b},y=\frac{b}{b+c},z=\frac{c}{c+a}$. Ta cần chứng minh :

$$2(x^2+y^2+z^2)+6\geq 5(x+y+z)\;\;\;(*)$$

Ta xét trường hợp $x+y+z\leq \dfrac{3}{2}$. Khi đó ta dễ dàng chỉ ra $(*)$ đúng bằng đánh giá $x^2+y^2+z^2\geq \dfrac{(x+y+z)^2}{3}$.

Còn nếu mà $x+y+z\geq \dfrac{3}{2}$ thì khi đó $(1-x)+(1-y)+(1-z)\leq \dfrac{3}{2}$.

Nếu đặt $X=1-x,Y=1-y,Z=1-z$ thì $X+Y+Z\leq \dfrac{3}{2}$. Khi đó ta cũng sẽ có :

$$X^2+Y^2+Z^2+3\geq \dfrac{5}{2}\left ( X+Y+Z \right )$$

$$\Leftrightarrow \left ( \frac{b}{a+b} \right )^2+\left ( \frac{c}{b+c} \right )^2+\left ( \frac{a}{a+c} \right )^2+3\geq \dfrac{5}{2}\left ( \frac{b}{a+b}+\frac{c}{b+c}+\frac{c}{c+a} \right )\;\;\;(**)$$

Chỉ cần đổi chỗ $a$ và $c$ cho nhau trong $(**)$ thì ta thu được BĐT đề bài.

Tức là ta có điều phải chứng minh.

Đề bài : Cho tứ giác ABCD nội tiếp (O). P di chuyển trên cung CD ko chứa A,B. PA cắt DB,DC tại E,F. PB cắt CA,CD tại G,H. GF giao EH tại Q. Chứng minh PQ luôn đi qua 1 điểm cố định khi P di chuyển.

Lời giải :

 

 

Gọi $U,V$ theo thứ tự là giao của tiếp tuyến tại $B$ với $AC$ và tiếp tuyến tại $A$ với $BD$. Gọi $T$ là giao của $BU$ và $AV$.

Áp dụng định lí Pascal cho bộ sáu điểm $(D,B,B,P,A,C)$ thì ta được $U,E,H$ thẳng hàng. 

Tương tự thì $V,G,F$ thẳng hàng.

Tiếp tục gọi $W$ là giao của $AB$ và $CD$.

Áp dụng định lí Pascal cho bộ sáu điểm $(A,A,C,D,B,B)$ thì ta có $U,V,W$ thẳng hàng.

Xét hai tam giác $BUH$ và $AVF$ có $AB,UV,HF$ đồng quy.

Và :

$$P=AF\cap BH,Q=VF\cap UH,T=AV\cap BU$$

Theo định lí Desargues ta có $P,Q,T$ thẳng hàng. Dễ thấy $T$ cố định nên $PQ$ luôn đi qua một điểm cố định.

Cho : $\left\{\begin{matrix}n\in \mathbb{\mathbb{N}^{\ast }} & & \\ & & \end{matrix}\right.7^{n}-3^{n}\vdots n$

 

a) Chứng minh rằng : n chẵn 

b)Tìm n 

Lời giải :

 

Gọi $p$ là ước nguyên tố nhỏ nhất của $n$

Gọi $t$ là nghịch đảo của $3$ modulo $p$. Gỉa sử $t\in \left \{ 1,2,..,p-1 \right \}$. Ta có :

$$3t\equiv 1\pmod p$$

Từ đó mà :

$$(7t)^n\equiv (3t)^n\equiv 1\pmod p$$

Suy ra rằng :

$$ord_p(7t)\mid n$$

Tuy nhiên ta cũng có $ord_p(7t)\mid p-1$ (theo định lí Fermat nhỏ). Gọi $r$ là một ước nguyên tố của $ord_p(7t)$, ta có $r \mid p-1$ nên $r<p-1<p$, mà cũng có $r\mid n$. Điều này là mâu thuẫn với tính nhỏ nhất của $p$.

Như vậy thì phải có $ord_p(7t)=1$. Suy ra :

$$7t\equiv 1\equiv 3t\pmod p\Rightarrow 4t\equiv 0\pmod p$$

Mà $gcd(t,p)=1$ nên $p\mid 4$, suy ra $p=2$. Như vậy $n$ là số chẵn.

 

Mình nghĩ bài này không thể tìm $n$ được (Chỉ là suy nghĩ của mình thôi) . Chỉ có thể tìm được $n$ với những bài như sau :

 

Tìm số nguyên dương $n$ thoả mãn :

$$n\mid p^n-(p-1)^n$$

Với $p$ là một số nguyên tố.

Tìm tất cả các hàm f(x): $[1;+\infty )\rightarrow [1;+\infty )$

      1 ) $x\leq f(x)\leq 2x+2$

      2) $xf(x+1)=(f(x)^{2})-1$     

Lời giải :

 

Ta có :

$$x+1\leq f(x+1)\leq 2x+4\;\;\forall x\in \left [ 1,+\infty \right )$$

$$\Rightarrow x^2+x\leq xf(x+1)=f^2(x)-1\leq 2x^2+4x,\;\forall x\in \left [ 1,+\infty \right )$$

$$\Rightarrow \left ( x+\frac{1}{4} \right )^2+\dfrac{3}{4}\leq f^2(x)\leq 2(x+1)^2-2,\;\forall x\in \left [ 1,+\infty \right )$$

$$\Rightarrow x+\dfrac{1}{4}\leq f(x)\leq \sqrt{2}(x+1),\;\forall x\in \left [ 1,+\infty \right )$$

$$\Rightarrow \frac{x+1}{\sqrt{2}}\leq f(x)\leq \sqrt{2}(x+1),\;\forall x\in \left [1,+\infty \right )$$

 

Thực hiện liên tiếp quá trình này, ta được :

$$\dfrac{x+1}{\sqrt[2^n]{2}}\leq f(x)\leq \sqrt[2^n]{2}(x+1),\;\forall x\in \left [ 1,+\infty \right )$$

Với mỗi $x$ thuộc nửa khoảng từ $1$ tới dương vô cực, ta cho $n\rightarrow +\infty$ ta được :

$$x+1\leq f(x)\leq x+1,\;\forall x\in \left [ 1,+\infty \right )$$

Như vậy ta phải có :

$$f(x)=x+1,\;\forall x\in \left [ 1,+\infty \right )$$

Thử lại thấy thoả. Đó là đáp số duy nhất của bài toán.

$P(x,y)$ có tính chất $f\left ( y^{2}+2xf\left ( y \right )+f\left ( x \right )^{2} \right )=\left ( y+f\left ( x \right ) \right )\left ( x+f\left ( y \right ) \right )$

Giả sử tồn tại hai số phân biệt $a,b$ sao cho $f(a)=f(b)=0$ Giả sử $a\neq 0$

$P(a,a)\Rightarrow f(a^2)=a^2$

$P(b,a)\Rightarrow f(a^2)=ab\neq a^2$ ( vô lí )

Nên không tồn tại hai số phân biệt $a,b$ mà $f(a)=f(b)=0$

Giả sử tồn tại hai số phân biệt $u,v$ mà $f(u)=f(v)$

$P(-f(u),u)\Rightarrow f(u^2-2f(u)^2+f(-f(u))^2)=0$

$P(-f(u),v)\Rightarrow f(v^2-2f(u)^2+f(-f(u))^2)=0$

$\Rightarrow u=-v$

So sánh giữa $P(x,u)$ và $P(x,v)$ thấy thấy mâu thuẫn khi $x\neq -f(u)$

Nên hàm đơn ánh.

Nhận xét giữa $P(x,y)$ và $P(y,x)$ ta có $f(y^2+2xf(y)+f(x)^2)=f(x^2+2yf(x)+f(y)^2)$

$\Rightarrow y^2+2xf(y)+f(x)^2=x^2+2yf(x)+f(y)^2\Rightarrow (f(x)-y)^2=(f(y)-x)^2$

Từ $P(x,f(x)),P(f(x),x)\Rightarrow f(f(x))=x$

Từ $P(x,f(y)),P(f(x),y)\Rightarrow (f(x)-f(y))^2=(x-y)^2$

$\Rightarrow f(x)=\pm x$

Có thể xét them TH $f(a)=a,f(b)=-b$ thì $P(a,b)\Rightarrow f((a-b)^2)=a^2-b^2\Rightarrow a=b$ mâu thuẫn.

Bài toán có tất cả ba nghiệm hàm, ngoài hai nghiệm bạn kể trên còn nghiệm $f(x)=\dfrac{1}{2}-x,\;\forall x\in \mathbb{R}$.

 

Lời giải của mình :

 

Đề câu hàm đúng phải là :

 

Tìm tất cả các hàm số $f:\mathbb{Z}\rightarrow \mathbb{Z}$ và thoả mãn :

1) $f(f(n))=4n+3,\;\forall n\in \mathbb{Z}$

2) $f(f(n)-n)=2n+3,\;\forall n\in \mathbb{Z}$

 

Đây là lời giải của mình :

 

Trong $(2)$ cho $n=-1$ thì có :

$$f(f(-1)+1)=1$$

Vậy ta có $f(a)=1$ với $a=f(-1)+1$.

Trong $(2)$ thay $n$ bởi $2n$ :

$$f(f(2n)-2n)=4n+3=f(f(n)),\;\forall n\in \mathbb{Z}$$

Tuy nhiên dễ thấy $f$ đơn ánh nên :

$$f(2n)=f(n)+2n,\;\forall n\in \mathbb{Z}\;\;\;\;(3)$$

Trong $(1)$ thay $n$ bởi $f(n)-n$ và sử dụng $(2)$ :

$$f(2n+3)=4f(n)-4n+3,\;\forall n\in \mathbb{Z}\;\;\;(4)$$

 

Trong $(4)$ cho $n=a$ :

$$f(2a+3)=4f(a)-4a+3=-4a+7$$

Trong $(2)$ cho $n=2a+3$ được :

$$f(f(2a+3)-2a-3)=2(2a+3)+3=4a+9\Leftrightarrow f(-2a+4)=4a+9$$

 

Mặt khác trong $(1)$ cho $n=a$ thì được $f(1)=4a+3$. Từ đó theo $(3)$ :

$$f(4)=f(2)+4=f(1)+6=4a+9$$

 

Như vậy ta được $f(4)=f(-2a+4)\Leftrightarrow 4=-2a+4\Leftrightarrow a=0$. Tức $f(0)=1$

 

Ta sẽ chứng minh bằng quy nạp $f(n)=2n+1,\;\forall n\in \mathbb{N}$. Rõ ràng với $n=0$ thì điều này đúng.

Gỉa sử điều này đúng với $n$, xét với $n+1$ :

Từ $(2)$ ta có ngay :

$$f((2n+1)-n)=2n+3\Leftrightarrow f(n+1)=2(n+1)+1$$

Theo nguyên lí quy nạp ta được :

$$f(n)=2n+1,\;\forall n\in \mathbb{N}$$

Tiếp theo ta sẽ chứng minh $f(n)=2n+1,\;\forall n\in \mathbb{Z}^-$.

Với $f(0)=1$ và các đẳng thức $(3),(4)$ ta dễ dàng tính được $f(-1)=-1,f(-2)=-3,f(-3)=-5$.

Gỉa sử rằng :

$$f(-n)=-2n+1,\;\forall n\in \mathbb{N}: 3\leq n\leq k$$

Ta cần chỉ ra rằng $f(-k-1)=-2k-1$.

Thật vậy, nếu $k$ lẻ thì theo $(3)$ :

$$f(-k-1)=f\left ( \dfrac{-k-1}{2} \right )-k-1$$

Tuy nhiên theo giả thiết quy nạp ta có $f\left ( \frac{-k-1}{2} \right )=-k$. Suy ra $f(-k-1)=-2k-1$.

Còn nếu $k$ chẵn thì theo $(4)$ :

$$f(-k-1)=4f\left ( \dfrac{-k-4}{2} \right )-4.\left ( \frac{-k-4}{2} \right )+3=4.\left ( -k-3 \right )+2(k+4)+3=-2k-1$$

Quy nạp hoàn tất, ta được :

$$f(n)=2n+1,\;\forall n\in \mathbb{Z}^-$$

 

Đáp số của bài toán là :

$$f(n)=2n+1,\;\forall n\in \mathbb{Z}$$

Cho dãy số $(U_n)$ xác định bởi :

                  $U_n=\sqrt[4]{a_1+\sqrt[4]{a_2+...+\sqrt[4]{a_n}}}$ $;$

 

trong đó các số $a_n$ thỏa mãn điều kiện 

                  $0<a_n<2000.30^{4n};n\epsilon \mathbb{Z}^{+}$      

     Chứng minh $(U_n)$ hội tụ       

Đề có nhầm không em ? Anh nghĩ đề nên là $30^{4^n}$. Nếu đúng là đề như thế em có thể tham khảo lời giải một bài tương tự như vậy ở đây .

Tìm f: R -> R thỏa mãn:

$f(x^{3}+f(y)) = y+f^{3}(x)\;\;\;\;\;(1)$ với mọi x,y thực

 

Lời giải :

 

Ta sẽ chứng minh $f(0)=0$.

Từ đề bài dễ thấy $f$ là một song ánh. Do vậy sẽ tồn tại duy nhất số thực $b$ sao cho $f(b)=0$. Đặt $f(0)=a$.

Trong $(1)$ cho $x=y=0$ : 

$$f(a)=a^3$$

Trong $(1)$ cho $y=a,x=b$ :

$$f(b^3+a^3)=a$$

Suy ra $f(b^3+a^3)=a=f(0)$, kéo theo $b^3+a^3=0$.

Trong $(1)$ cho $x=0,y=b$ :

$$f(0)=b+a^3\Leftrightarrow a^3+b=a$$

Trong $(1)$ cho $x=0,y=a$ :

$$f(f(a))=a+f^3(0)\Leftrightarrow f(a^3)=a+a^3$$

Trong $(1)$ tiếp tục cho $x=a,y=b$ :

$$f(a^3)=b+f^3(a)=b+a^9$$

Từ đó suy ra $b+a^9=a+a^3$.

Giải hệ gồm ba phương trình hai ẩn sau :

$$\left\{\begin{matrix} b+a^9=a+a^3\\ a^3+b^3=0\\ a^3+b=a \end{matrix}\right.\Leftrightarrow a=b=0$$

Vậy tóm lại là $f(0)=0$.

 

Từ đó dễ dàng suy ra được :

$$f(f(y))=y,\;\forall y\in \mathbb{R}$$

$$f(x^3)=f^3(x),\;\forall x\in \mathbb{R}$$

Kết hợp hai điều trên với phương trình hàm đã cho ta suy ra được :

$$f(x+y)=f(x)+f(y),\;\forall x\in \mathbb{R}$$

Khi đó sẽ có :

$$f(n)=n,\;\forall n\in \mathbb{Z}$$

 

Khi ấy, ta có :

$$f((x+1)^3)=\left [ f(x)+1 \right ]^3=f^3(x)+3f^2(x)+3f(x)+1,\;\forall x\in \mathbb{R}$$

Cũng có :

$$f((x+1)^3)=f(x^3+3x^2+3x+1)=f^3(x)+3f(x^2)+3f(x)+1,\;\forall x\in \mathbb{R}$$

So sánh hai kết quả trên thì được :

$$f(x^2)=f^2(x),\;\forall x\in \mathbb{R}$$

Điều này cho ta tính chất :

$$f(x)\geq 0,\;\forall x\geq 0$$

 

Kết hợp với tính cộng tính của $f$ ta dễ suy ra hàm duy nhất thoả đề là :

$$\boxed{f(x)=x,\;\forall x\in \mathbb{R}}$$

 

Lưu ý : Bài này có thể tổng quát lên bằng cách thay số mũ $3$ bằng số tự nhiên $n$ tuỳ ý.

Cho $x=y=0$ ta có $f(f(0))=0$

Cho $x=0,y=f(0)$ ta có $f(f(f(0)))+f(0)=f(f(0))+(f(0))^2\Rightarrow f(0)(f(0)-2)=0$

$\Rightarrow f(0)=0$ hoặc $f(0)=2$

   -Với TH $f(0)=2$

Thay $x,y$ lần lượt bằng $x-1,1$ ta được $f(x+f(x)-1)=x+f(x)-1$

Đặt $g(x)=x+f(x)-1\Rightarrow f(g(x))=g(x)\Rightarrow f(f(g(x)))=f(g(x))$

Thay $x,y$ lần lượt bằng $0,g(x)$ ta được $f(f(g(x)))+2=f(g(x))+2g(x)$

$\Rightarrow g(x)=1\Rightarrow x+f(x)-1=1\Rightarrow f(x)=2-x$

   -Với TH $f(0)=0$

Cho $x=0$ ta có $f(f(y))=f(y)$

Cho $y=0$ ta có $f(f(x)+x)=f(x)+x$

Cho $y=-x$ ta có $f(x)+f(-x^2)=x(1-f(x))$ (1)

Thay $x$ bằng $-x$ ở $(1)$ ta có $f(-x)+f(-x^2)=-x(1-f(-x))$ (2)

Lấy $(1)-(2)$ ta có $f(x)-f(-x)=2x-x(f(x)+f(-x)$ (3)

Giả sử tồn tại một vài số $t$ thỏa $f(t)=t$ thì theo $(3)$ suy ra được $f(-t)=-t$ 

Vậy ta sẽ có $f(-f(x))=-f(x),f(-x-f(x))=-x-f(x)$

Thay $x,y$ lần lượt là $-x,x-f(x)$ ta được $f(-x+f(-f(x)))+f(x(f(x)-x))=-x+f(-f(x))+(x-f(x))f(-x)$

$\Rightarrow f(x(f(x)-x))=(x-f(x))f(-x)$ (4)

Thay $x,y$ lần lượt bằng $x,f(x)-x$ ta được $f(x+f(f(x)))+f(x(f(x)-x))=x+f(f(x))+(f(x)-x)f(x)$

$\Rightarrow f(x(f(x)-x))=(f(x)-x)f(x)$ (5)

Từ $(4)$ và $(5)$ suy ra $(x-f(x))f(-x)=(f(x)-x)f(x)$

$\Rightarrow f(x)-x=0$ hoặc $f(x)=-f(-x)$

Nếu $f(x)=-f(-x)$ thay vào $(3)$ ta được $f(x)=x$

Vậy kết luận chung có 2 hàm thỏa đề $f(x)=x$ và $f(x)=2-x$

PS: Quên không thử lại

Sao lại có dòng màu đỏ thế ạ ? 

Còn chỗ dòng màu tím sẽ xuất hiện hiện tượng "nhảy" hàm ạ, nên em nghĩ chỗ đó cần bổ sung thêm nữa.

Lời giải. Đặt $n+mf(m)=k \left( m^2+f(n) \right)=km^2+ k \cdot f(n)$.

Với $m=0$ thì $n=k \cdot f(n)$. Do đó $m^2k=mf(m)$. Mặt khác $m=k \cdot f(m)$ nên $m^2k^2=m^2$ hay $k^2=1$. Vậy $f(m)=m$ hoặc $f(m)=-m$. Để ý rằng $f: \mathbb{N} \to \mathbb{N}$ nên chỉ có thể $f(m)=m$. Thử lại thấy thoả mãn.

Vậy $f(m)=m, \; \forall m \in \mathbb{N}$.

Em giải chưa đúng rồi. Gía trị $k$ ở đây có thể thay đổi theo từng cặp giá trị $(m,n)$ thay vào. Lời giải của em vô tình thừa nhận : Gía trị của $\frac{mf(m)+n}{m^2+f(n)}$ luôn là một hằng số nguyên với mọi giá trị tự nhiên $(m,n)$.

 

Có thể giải như sau :

 

Lời giải :

 

Trong $(1)$ cho $m=0$ : 

$$f(n)\mid n,\;\forall n\in \mathbb{N}\Rightarrow n\geq f(n),\;\forall n\in \mathbb{N}$$

Trong $(1)$ lại cho $n=0$ :

$$m^2+f(0)\mid mf(m),\;\forall m\in \mathbb{N}\Rightarrow mf(m)\geq m^2+f(0)\geq m^2,\;\forall m\in \mathbb{N}\Rightarrow f(m)\geq m,\;\forall m\in \mathbb{N}$$

Suy ra hàm duy nhất thoả đề là $f(n)=n,\;\forall n\in \mathbb{N}$.

-Chọn $x=y=1= > \frac{f(1)+f(1)}{\sqrt{f(1)}}=\frac{1+1}{\sqrt{1}}= > \frac{2f(1)}{\sqrt{f(1)}}=2= > f(1)=\sqrt{f(1)}= > f(1)=1$

   (Do hàm $f:(0,+\infty )\rightarrow (0,+\infty )$  nên $f(1)$ khác $0$)

 

- Chọn $y=1$ và áp dụng $f(1)=1$

 

 $= > \frac{f(x)+f(1)}{\sqrt{f(x)}}=\frac{x+1}{\sqrt{x}}= > \frac{f(x)+1}{\sqrt{f(x)}}=\frac{x+1}{\sqrt{x}}= > \sqrt{f(x)}-\sqrt{x}=\frac{1}{\sqrt{x}}-\frac{1}{\sqrt{f(x)}}

$= > (\sqrt{f(x)}-\sqrt{x})(1-\frac{1}{\sqrt{xf(x)}})=0$

 

 Do đó $f(x)=x$ hoặc $f(x)=\frac{1}{x}$ .Thử lại ta thấy thỏa mãn bài toán

Lời giải thiếu rồi. Từ khúc màu đỏ chưa thể suy ra tồn tại hai hàm như vậy được.

Có thể bổ sung tiếp như sau :

 

Ta thấy hai hàm $f(x)\equiv x,f(x)\equiv \dfrac{1}{x}$ thoả đề.

Ta chứng minh đây là hai hàm duy nhất thoả đề. Thật vậy, giả sử tồn tại các số dương $a,b \neq 1$ sao cho $f(a)=a,f(b)=\dfrac{1}{b}$. Trong $(1)$ cho $x=a,y=b$ :

$$\frac{a+1/b}{\sqrt{f(ab)}}=\frac{a+b}{\sqrt{ab}}\Rightarrow f(ab)=\frac{(ab+1)^2a}{b(a+b)^2}$$

Nếu mà $f(ab)=ab$ thì :

$$\frac{(ab+1)^2.a}{b(a+b)^2}=ab\Leftrightarrow \frac{ab+1}{a+b}=b\Leftrightarrow b=1$$

Mâu thuẫn.

Còn nếu $f(ab)=\dfrac{1}{ab}$ thì :

$$\dfrac{(ab+1)^2a}{b(a+b)^2}=\dfrac{1}{ab}\Leftrightarrow \dfrac{ab+1}{a+b}=\dfrac{1}{a}\Leftrightarrow a=1$$

Cũng mâu thuẫn.

Tóm lại là chỉ có hai nghiệm hàm như trên thoả mãn đề ra

Tính tích phân sau :

$$I=\int_{1}^{2}\dfrac{dx}{x(x^3+1)}$$

Tìm nguyên hàm của hàm số $f(x)=\sin^2x.\tan x$

 

Tìm tất cả các hàm số $f:\mathbb{R}\rightarrow \mathbb{R}^+$ và thoả :

$$xf(y)+f\left ( xy-\dfrac{1}{f(x)} \right )=1+f(f(x^2y-1)),\;\forall x,y\in \mathbb{R}$$

Tìm nghiệm nguyên của phương trình:

$3^{x}+4^{y}=7^{z}$

Lời giải :

 

Xét hơi nhiều trường hợp tý nhé !

$\boxed{1}$ Xét trường hợp $x < 0$ :

$\bullet$ $y > 0$ và $z > 0$ : Một vế nguyên, một vế không nguyên (loại)

$\bullet$ $y > 0$ và $z < 0$ : 

$\frac{1}{3^{|x|}}+4^{y}=\frac{1}{7^{|z|}}\Leftrightarrow 7^{|z|}+4^{y}.3^{|x|}.7^{|z|}=3^{|x|}$

Vô lí vì hiển nhiên $7^{|z|}+4^{y}.3^{|x|}.7^{|z|}>3^{|x|}$

$\bullet$ $y < 0$ và $z > 0$ :

$\frac{1}{3^{|x|}}+\frac{1}{4^{|y|}}=7^{z}\Leftrightarrow 3^{|x|}+4^{|y|}=7^{z}.3^{|x|}.4^{|y|}$

Một vế chẵn, một vế lẻ (loại)

$\bullet$ $y < 0$ và $z < 0$ :

$\frac{1}{3^{|x|}}+\frac{1}{4^{|y|}}=\frac{1}{7^{|z|}}\Leftrightarrow 7^{|z|}.(3^{|x|}+4^{|y|})=3^{|x|}.4^{|y|}$

Một vế chẵn, một vế lẻ (loại)

 

$\boxed{2}$ Xét trường hợp : $x\geq 0$ 

$\bullet$ $y\geq 0;z\geq 0$  (sẽ giải sau)

$\bullet$ $y\geq 0;z\leq 0$ : Một vế nguyên, một vế không nguyên (loại)

$\bullet$ $y\leq 0;z\geq 0$ : Một vế nguyên, một vế không nguyên (loại)

$\bullet$ $y\leq 0;z\leq 0$ : $3^{|x|}+\frac{1}{4^{|y|}}=\frac{1}{7^{|z|}}\Leftrightarrow 3^{|x|}.7^{|z|}.4^{|y|}+7^{|z|}=4^{|y|}$

Vô lí vì hiển nhiên $3^{|x|}.7^{|z|}.4^{|y|}+7^{|z|}>4^{|y|}$

 

Bây giờ ta sẽ giải trường hợp cả ẩn $x,y,z$ đều là những số nguyên dương

$\blacksquare$ Nếu $y\geq 2$ thì : $4^{y}\vdots 8$

Ta có : $3^{x}+4^{y}\equiv 1;3(mod8)$ mà $7^{z}\equiv 1;7(mod8)$

Do đó $7^{z}=3^{x}+4^{y}\equiv 1(mod8)\Rightarrow x,z$ chẵn

Đặt $x=2a;y=2b$ (với $a,b$ nguyên dương), ta được :

$$3^{2a}+2^{2y}=7^{2b}\Leftrightarrow (7^{b}-3^{a})(7^{b}-3^{a})=2^{2y}$$

Do đó :

$$\left\{\begin{matrix} 7^{b}-3^{a}=2^{m} & & \\ 7^{b}+3^{a}=2^{n} & & \end{matrix}\right.$$

Với $m,n$ tự nhiên và $m<n,m + n = 2y$

Trừ vế với vế :

$$2.3^{a}=2^{n}-2^{m}$$

$\Leftrightarrow 2.3^{a}=2^{m}(2^{n-m}-1)\Rightarrow \left\{\begin{matrix} m=1 & & \\ 2^{n-1}-1=3^{a}& & \end{matrix}\right.$

Xét riêng phương trình $2^{n-1}-1=3^{a}$. Bằng cách xét đồng dư mô-đun $3$, chỉ ra được $n-1$ chẵn.

Từ đó dễ tìm được $a=1;n=3;m=1$. Từ đó $y = 1$ (loại vì đang xét $y\geq 2$)

$\blacksquare$ Ta xét $y = 1$

Ta được phương trình : $$3^{x}+4=7^{z}$$

Dễ thấy khi $z = 1$ thì $x = 1$, ta xét $z > 1$

$\blacktriangledown$ Xét $z$ chẵn, thì $7^{z}\equiv 1(mod4)\Rightarrow 3^{x}+4\equiv 1(mod4)\Rightarrow x$ chẵn

Đặt $z=2m;y=2n$ ($m,n$ nguyên dương), thay vào thì : $(7^{m}-3^{n})(7^{m}+3^{n})=4$

Phương trình ước số này không cho nghiệm thỏa mãn

$\blacktriangledown$ Xét $z$ lẻ thì : $7^{z}\equiv 3(mod4)\Rightarrow 3^{x}+4\equiv 3(mod4)\Rightarrow x$ lẻ

Bằng cách đặt $x = 6k + r$ và xét đồng dư theo mô-đun $7$ ta dễ dàng tìm được $r=1$, tức $x = 6k+1$

Vì $x$ lẻ nên $$3^{x}\equiv 2;3(mod5)\Rightarrow 7^{z}=3^{x}+4\equiv 1;2(mod5)(\bigstar )$$

Vì $z$ lẻ nên đặt $z = 2z_{1}+1$, ta được : $$7^{z}=7^{2z_{1}+1}\equiv (-1)^{z_{1}}.7\equiv 2;3(mod5)(\blacklozenge )$$

Từ $(\blacklozenge )(\bigstar )$ suy ra :

$$(-1)^{z_{1}}.7\equiv 2(mod5)\Rightarrow z_{1}\vdots 2\Rightarrow z\equiv 1(mod4)$$

Ta có $y = 6k+1$ nên : 

$$7^{z}=3^{x}+4=3^{6k+1}+4\equiv 7(mod13)$$.

Đặt $z = 12t + r'$ thì $$7^{z}=7^{12t+r'}\equiv 7^{r'}\equiv 7(mod13)\Rightarrow r'=1\Rightarrow z=12t+1$$

 

Như vậy ta đã chứng minh xong $z = 12t+1$ và $x = 6k+1$

Từ phương trình đã cho, suy ra :

$$7^{z}-7=3^{x}-3\Leftrightarrow 7^{12t+1}-7=3^{6k+1}-3\Leftrightarrow 7(7^{12t}-1)=3(3^{6k}-1)$$

Ta thấy $VT\equiv 0(mod3);VP\equiv 6(mod9)$ (loại)

 

KẾT LUẬN : $\boxed{(x;y;z)=(1;1;1)}$

 Bài toán : Tìm tất cả các hàm $f:R\rightarrow R$ thỏa mãn điểu kiện sau:

 

                $f(xf(y))+f(f(x)+f(y))=yf(x)+f(x+f(y))\;\;\;\;(1)$

 

Lời giải :

 

Ta thấy hàm số $f\equiv 0$ thoả. Xét $f$ không đồng nhất $0$, khi đó tồn tại số thực $k$ sao cho $f(k)\neq 0$.

Trong $(1)$ cho $x=k$ :

$$f(kf(y))+f(f(k)+f(y))=yf(k)+f(k+f(y)),\;\forall y\in \mathbb{R}$$

Từ đây suy ra $f$ đơn ánh.

 

Đặt $f(0)=a,f(1)=b$. Trong $(1)$ cho $x=0,y=1$ :

$$a+f(a+b)=a+f(b)\Rightarrow f(a+b)=f(b)$$

Vì $f$ đơn ánh nên $a+b=b$ hay $a=0$.

Từ đây trong $(1)$ cho $x=1,y=0$ :

$$f(a)+f(a+b)=f(1+a)\Leftrightarrow f(b)=f(1)\Leftrightarrow b=1$$

Tức là ta có $f(1)=1$.

Bây giờ trong $(1)$ chọn $y=1$ thì :

$$f(x)+f(f(x)+1)=f(x)+f(x+1),\;\forall x\in \mathbb{R}\Rightarrow f(f(x)+1)=f(x+1),\;\forall x\in \mathbb{R}$$

Do $f$ đơn ánh nên $f(x)=x,\;\forall x\in \mathbb{R}$. Và hàm này thoả đề.

Có hai hàm số thoả đề là :

$$f(x)=0,\;\forall x\in \mathbb{R}$$

$$f(x)=x,\;\forall x\in \mathbb{R}$$

Cho $p$ là số nguyên tố có dạng $4k+3$. Chứng minh rằng tập hợp gồm $p-1$ số nguyên dương liên tiếp không thể chia thành hai tập hợp con không giao nhau sao cho tích các phần tử ở mỗi tập là bằng nhau.

Lời giải :

Gọi tập hợp đó là $S=\left \{ n,n+1,n+2,..,n+p-1 \right \}$. Gỉa sử có thể chia được như đề bài, khi đó tích $A=n(n+1)(n+2)...(n+p-1$ là số chính phương.

Nếu $S$ chứa một phần tử chia hết cho $p$ thì đó cũng là phần tử duy nhất chia hết cho $p$ trong $S$.

Suy ra $p\mid A$ nhưng $p^2\nmid A$, mâu thuẫn vì $A$ chính phương.

Nếu $S$ không chứa phần tử nào chia hết cho $p$ thì do bất kì hai phần tử nào trong $S$ cũng không đồng dư với nhau theo modulo $p$ nên theo định lí Wilson :

$$A=n(n+1)...(n+p-1)\equiv 1.2.3....(p-1)=(p-1)!\equiv -1\pmod p$$

$$p\mid A+1$$

Điều này là vô lí vì tất cả các số dạng $x^2+1$ không có ước nguyên tố dạng $4k+3$.

Tìm hằng số $k$ lớn nhất để BĐT sau đúng với mọi $a,b,c$ không âm

                                   $\frac{a^3+b^3+c^3}{(a+b)(b+c)(c+a)}+k\frac{ab+bc+ca}{(a+b+c)^2}\geq \frac{3}{8}+\frac{k}{3}$

Số $k$ tốt nhất không đẹp đâu nhé ! 

$$k_{max}=\dfrac{27+18\sqrt{3}}{8}$$

Lời giải ở đây.

(Cách khác)

Lời giải :

Ta chọn $n$ như sau :

$$n=2^{p-1}p_2p_3...p_k$$

Trong đó $p$ là số nguyên tố, và $p_2,p_3,...,p_k$ là $k$ số nguyên tố phân biệt lớn hơn $3$.

Hiển nhiên có vô số số $n$ như vậy, và hiển nhiên rằng $\omega (n)=k$.

Ta sẽ chứng minh với cách này thì với mọi cặp $(a,b)$ nguyên dương có tổng bằng $n$ thì ta đều có $d(n)\nmid d(a^2+b^2)$.

Thật vậy, giả sử tồn tại một cặp số nguyên dương $(a,b)$ thoả $a+b=n$ và $d(n)\mid d(a^2+b^2)$.

Dễ thấy $d(n)=2^{k-1}.p$. Suy ra :

$$p\mid d(a^2+b^2)\Rightarrow q^{p-1}\mid a^2+b^2$$

với $q$ là một ước nguyên tố nào đó của $a^2+b^2$. Thế thì :

$$q^{p-1}\leq a^2+b^2< (a+b)^2=4^{p}p_2^2p_3^2...p_k^2$$

Rõ ràng nếu $q<4$ thì với $p$ đủ lớn ta sẽ có $q^{p-1}>4^{p-1}p_2^2p_3^2...p_k^2$. Như vậy $q=2,3$.

Nếu $q=3$ thì suy ra $3\mid a^2+b^2$, suy ra $3\mid a,b$. Kéo theo $3\mid n$.

Dễ thấy điều này mâu thuẫn với cách chọn $n$ như trên.

Vậy phải có $q=2$. Dẫn tới :

$$2^{p-1}\mid a^2+b^2$$

Rõ ràng $a,b$ cùng tính chẵn lẻ, nhưng chúng không thể cùng lẻ vì khi đó $a^2+b^2\equiv 2\pmod 4$, vậy phải có $a,b$ cùng chẵn.

Đặt $a=2^A.x,b=2^B.y$ ($x,y$ lẻ), không giảm tổng quát có thể giả sử $A\geq B$.

Ta có :

$$2^{p-1}\mid 2^{2A}x^2+2^{2B}y^2=2^{2B}(2^{2A-2B}x^2+y^2)$$

Chú ý rằng $2^{2A-2B}x^2+y^2\equiv 1,2,3\pmod 4$. Do đó suy ra :

$$2B+1\geq p-1\Rightarrow A\geq B\geq \dfrac{p-1}{2}$$

Suy ra rằng $2^{(p-1)/2}\mid a,b$

Như vậy ta có thể có được biểu diễn sau :

$$a^2+b^2=2^{p-1}(a_1^2+b_1^2)$$

Do $d(n)$ là hàm nhân tính nên :

$$p\mid d(a^2+b^2)=d(2^{p-1}.(a_1^2+b_1^2))=p+d(a_1^2+b_1^2)\Rightarrow p\mid d(a_1^2+b_1^2)$$

Tương tự trên ta được :

$$2^{\frac{p-1}{2}}\mid a_1,b_1$$

Tiếp tục quá trình này, ta sẽ suy ra :

$$2^{\frac{p-1}{2}.N}\mid a,b$$

Với số nguyên dương $N$ tuỳ ý, rõ ràng điều này là vô lí.

Ta có điều cần chứng minh.

$\boxed{\text{Problem}}$

Cho $a,b$ là hai số nguyên dương thỏa $\left ( a,b \right )=1$.Hai dãy $\left \{ a_n \right \},\left \{ b_n \right \}$ thỏa 

$(a+b\sqrt{2})^{2n}=a_n+b_n\sqrt{2}$

Tìm các số nguyên tố $p$ thỏa mãn tồn tại $n\leq p$ thỏa mãn $p\mid b_n$

Xem ở đây.

Bài này post ở Box Số Học sẽ hợp hơn em nhé ! 

Chứng minh rằng với mọi số nguyên dương $k$ luôn tồn tại vô hạn số nguyên dương $n$ sao cho $n$ có đúng $k$ ước nguyên tố và thoả mãn $d(n)$ không chia hết $d(a^2+b^2)$ với mọi cặp số nguyên dương $(a,b)$ thoả mãn $a+b=n$.

Trong đó kí hiệu $d(n)$ là số các ước dương của $n$.