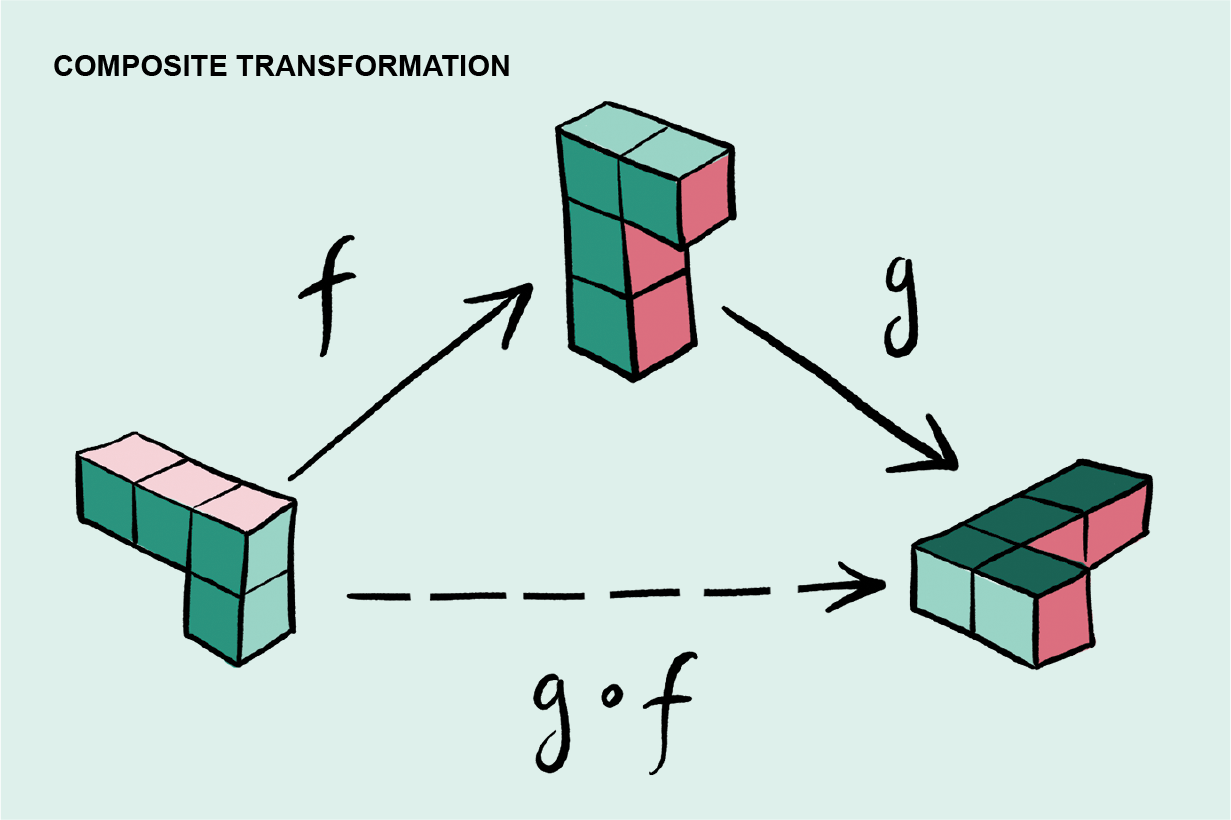
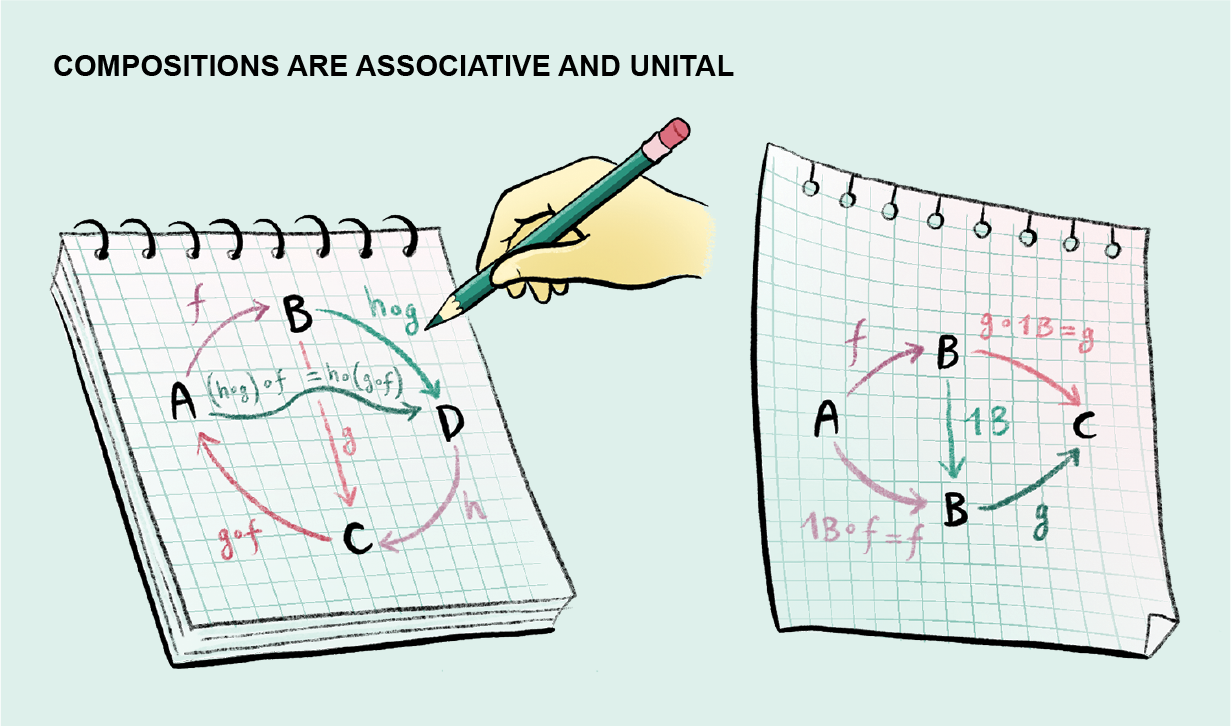
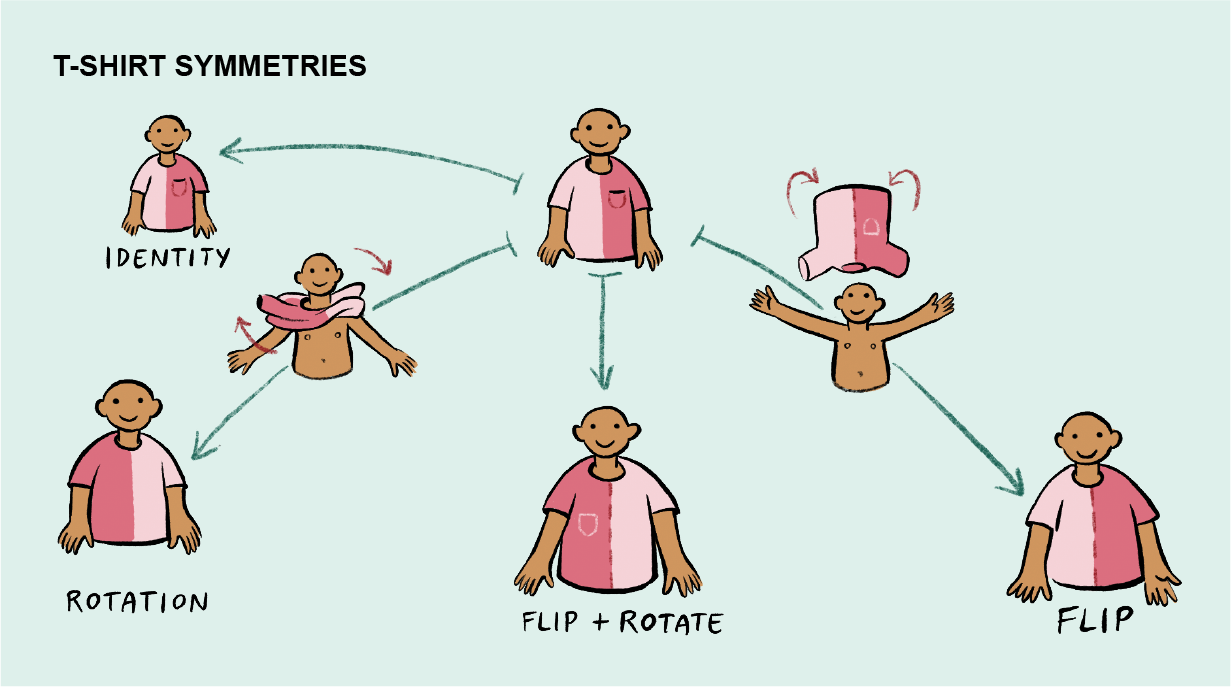
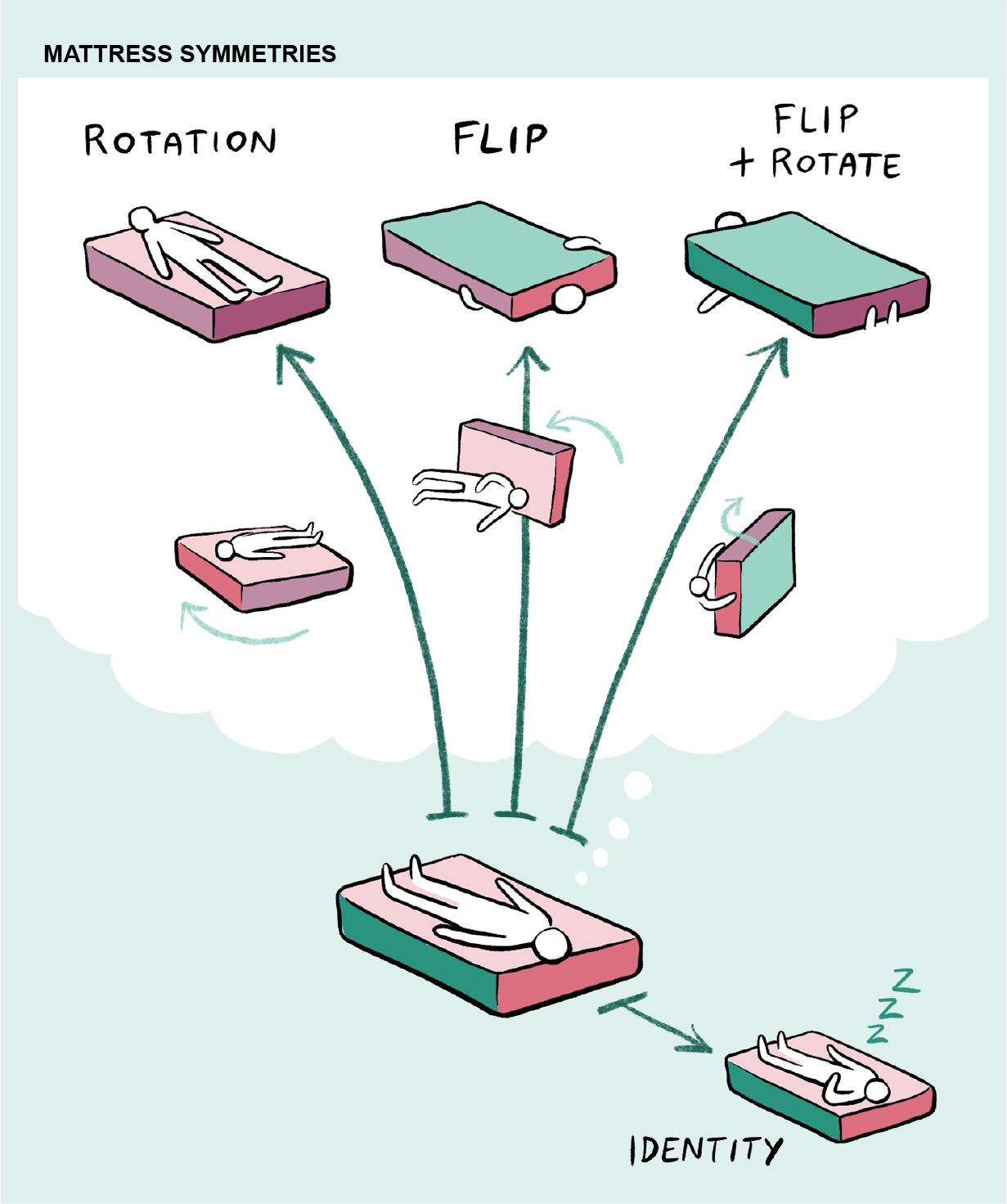
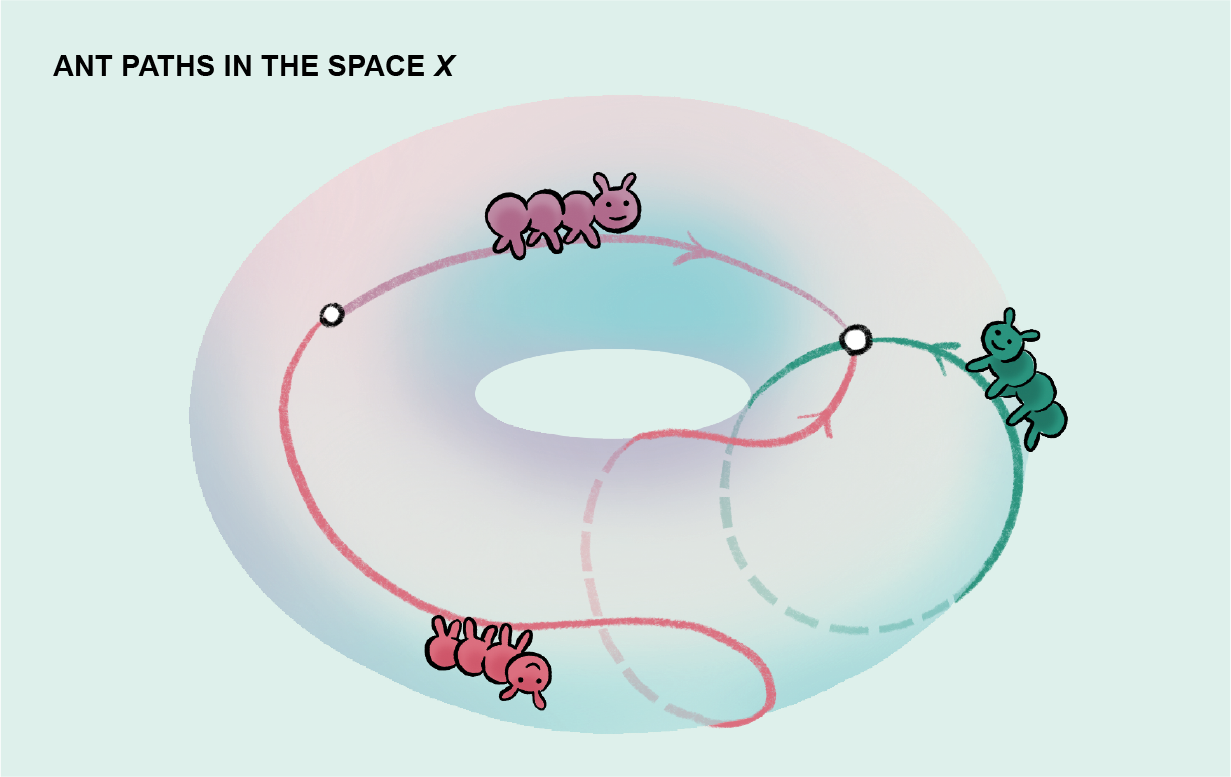
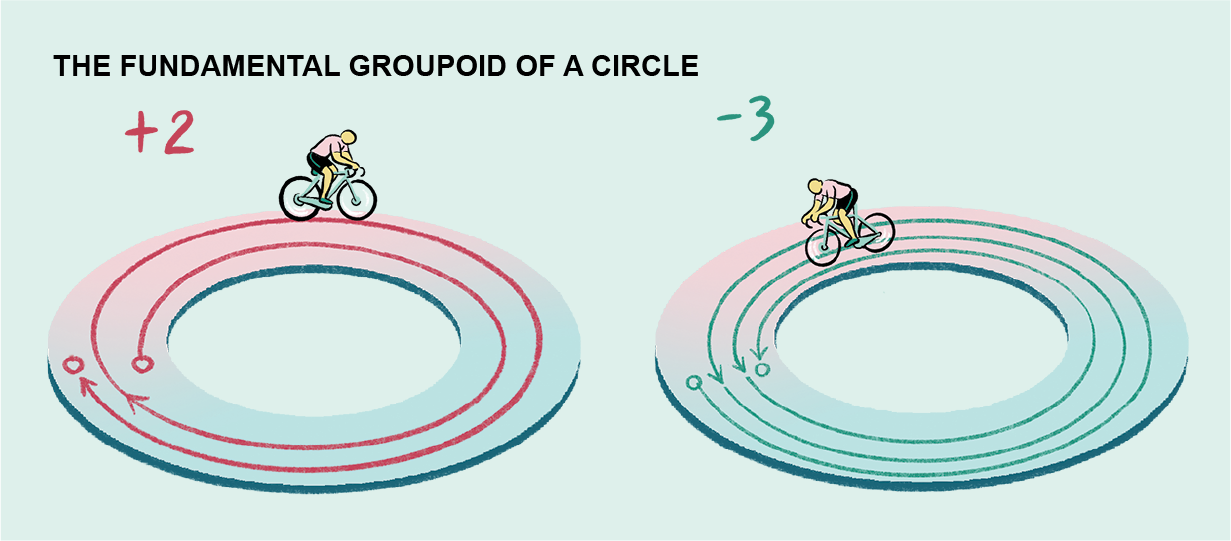
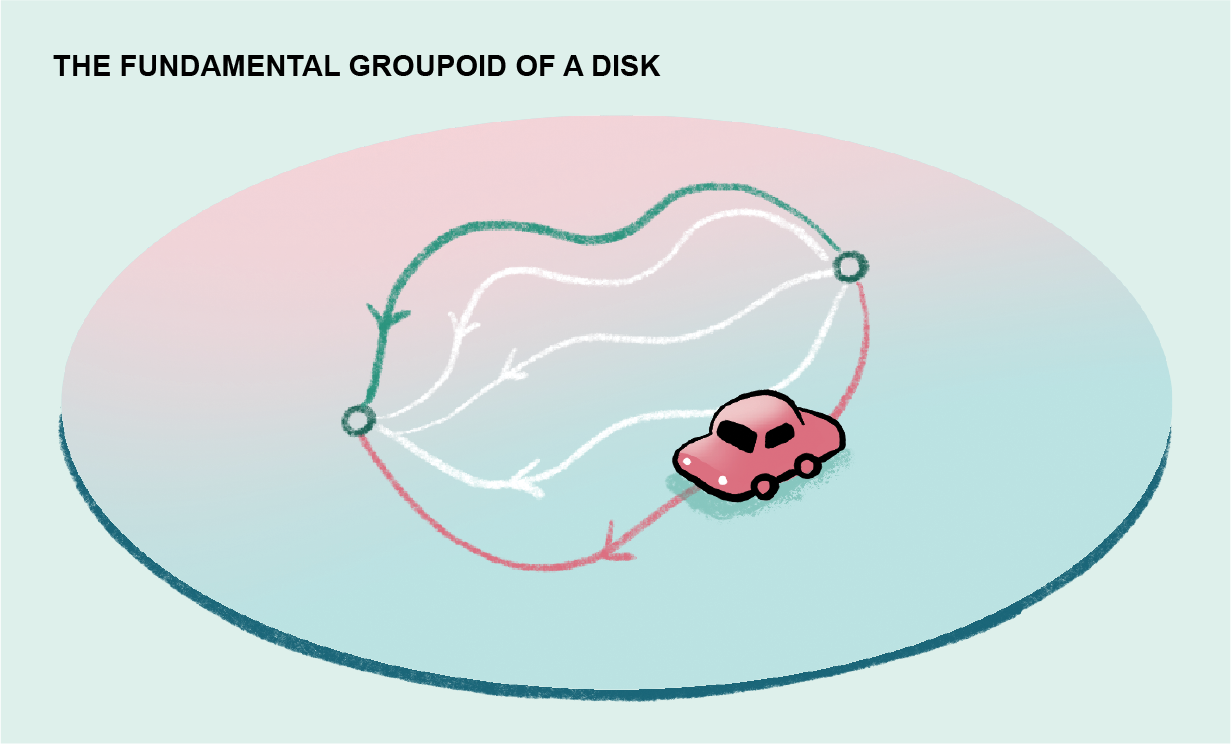
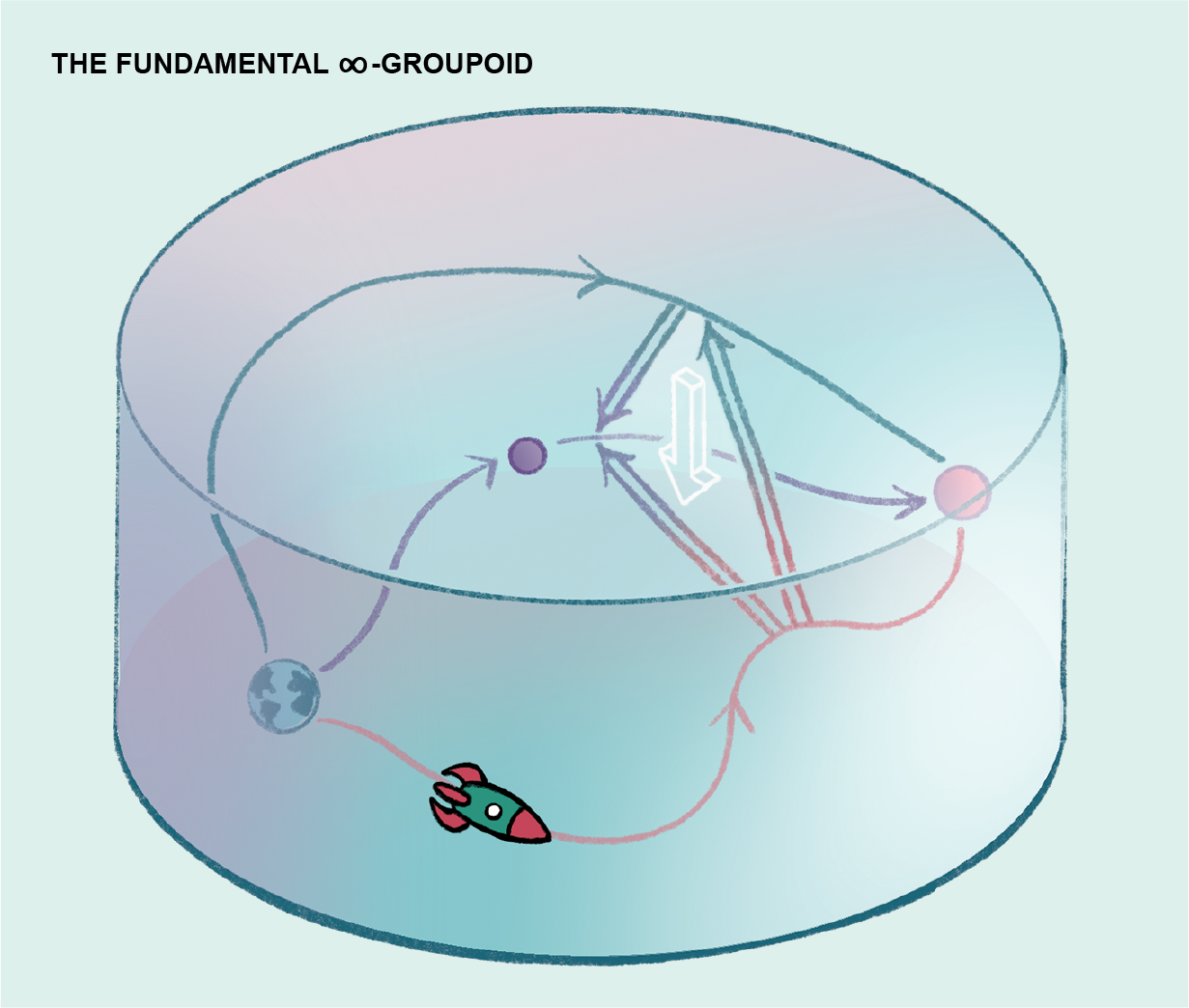
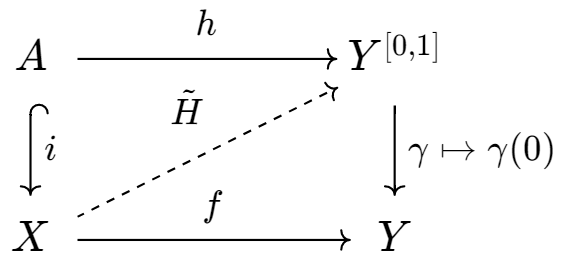
Bạn có thể viết như sau

$$\frac{1}{\sqrt[3]{x^2}} = \begin{cases} x^{-\tfrac{2}{3}} & \text{nếu } x > 0, \\ (-x)^{-\tfrac{2}{3}} & \text{nếu } x < 0. \end{cases}$$
Vì thế đạo hàm của hàm này trên từng khoảng $(-\infty,0)$ và $(0,+\infty)$ là

$$\begin{cases} -\frac{2}{3}x^{-\tfrac{5}{3}} = -\frac{2}{3 \sqrt[3]{x^5}} & \text{nếu } x > 0, \\ -\frac{2}{3}  (-x)^{-\tfrac{5}{3}} \cdot (-1) = \frac{2}{3 \sqrt[3]{(-x)^5}} = -\frac{2}{3 \sqrt[3]{x^5}} &  \text{nếu } x < 0. \end{cases}$$

Vì thế ta có công thức

$$\dfrac{d}{dx}\frac{1}{\sqrt[3]{x^2}} = -\frac{2}{3 \sqrt[3]{x^5}}$$

với mọi $x \neq 0$.

Bài không khó nhưng hệ số tìm được làm một số quan trọng và xuất hiện trong nhiều bài toán đếm khác nhau. 

Định lý phát biểu đầy đủ phải là: nếu hàm $f$ khả vi tại $x$ và $c$ là một hằng số thì hàm $cf$ cũng khả vi tại $x$, và $(cf)'(x) = c \cdot f'(x)$.

Dùng tiêu chuẩn tích phân: 

Chuỗi đa cho hội tụ khi và chỉ khi tích phân suy rộng $$\int_{2}^{+\infty} \frac{1}{x (\ln x)^p}\,dx$$ hội tụ. Đổi biến $\ln(x) = t$, tích phân trên trở thành $$\int_{\ln 2}^{+\infty} \frac{1}{t^p}\,dt.$$ Tích phân này hội tụ khi và chỉ khi $p > 1$.

Chứng minh rằng với mọi số nguyên dương $n$ thì

$$\prod_{k=1}^{n-1} \left(4\cos^2 \tfrac{k\pi}{n} + 1\right) = F_n^2,$$ trong đó $$\begin{cases} F_1 = F_2 = 1, \\ F_n = F_{n-1} + F_{n-2} & \text{nếu } n \ge 3. \end{cases}$$

Chia sẻ cách làm của mình.

Câu a)

Nhận xét. Với $i, k \in \mathbb{N}^\ast$ và $(i-1)i + 1 \le k \le i(i+1)$ thì

$$\left(i - \frac{1}{2}\right)^2 < (i-1)i + 1 \le k \le i(i+1) < \left(i + \frac{1}{2}\right)^2,$$

suy ra $i - \frac{1}{2} < \sqrt{k} < i + \frac{1}{2}$, nên $\left \lceil k \right \rfloor = i$.

Từ đó dễ thấy $\left \lceil k \right \rfloor = i$ khi và chỉ khi $(i-1)i + 1 \le k \le i(i+1)$.

Do đó, với $n \in \mathbb{N}^\ast$, nếu ta đặt $m = \left \lceil n\right \rfloor$ (tức là $(m-1)m + 1 \le n \le m(m+1)$) thì

$$\begin{align*} a_n & = \sum_{i=1}^{m-1} \left(\sum_{k=(i-1)i+1}^{i(i+1)} \frac{1}{\left \lceil k \right \rfloor}\right) + \sum_{k=(m-1)m+1}^{n}\frac{1}{\left \lceil k \right \rfloor} - 2\sqrt{n} \\ & = \sum_{i=1}^{m-1} \left(2i \cdot \frac{1}{i} \right) + (n - (m-1)m) \cdot \frac{1}{m} - 2\sqrt{n} \\ & = 2(m-1) + \frac{n}{m} - (m-1) - 2\sqrt{n} \\ & = m + \frac{n}{m} - 2\sqrt{n} - 1. \end{align*}$$

Đặt $f_m(x) = m + \frac{x}{m} - 2\sqrt{x} - 1$, với $m \in \mathbb{N}^\ast$ và $x \in [(m-1)m, m(m+1)]$. Ta có $$f'_m(x) = \frac{1}{m} - \frac{1}{\sqrt{x}}.$$ Khảo sát hàm số $f_m$, ta thấy nó đạt cực trị tại các điểm $(m-1)m$, $m^2$ và $m(m+1)$. So sánh các giá trị của $f_m$ tại các điểm này, ta có $f_m(x) \in \left[-1, \frac{-2\sqrt{m-1}}{\sqrt{m-1} + \sqrt{m}}\right]$ với mọi $x \in [(m-1)m, m(m+1)]$.

Nói riêng, với $n \in \mathbb{N}^\ast$ và $m = \left \lceil n\right \rfloor$ thì $$a_n = f_m(n) \in \left[-1, \frac{-2\sqrt{m-1}}{\sqrt{m-1} + \sqrt{m}}\right].$$ Khi $n \to +\infty$ thì $m \to +\infty$ và $\frac{-2\sqrt{m-1}}{\sqrt{m-1} + \sqrt{m}} \to -1$, nên theo nguyên lý kẹp ta có $a_n \to -1$.

Câu b)

Đặt $$g_m(x) = \sqrt{x}(f_m(x) + 1) = m\sqrt{x} + \frac{x\sqrt{x}}{m} - 2x,$$ với $m \in \mathbb{N}^\ast$ và $x \in [(m-1)m, m(m+1)]$. Ta có $$g'_m(x) = \frac{m}{2\sqrt{x}} + \frac{3\sqrt{x}}{2m} - 2.$$

Khảo sát hàm số này, ta thấy $g_m$ đồng biến trên $[m^2,m(m+1)]$. Nói riêng, $$0 = b_{m^2} \le b_{m^2 +1} \le \cdots \le b_{m(m+1)} = \frac{\sqrt{m(m+1)}}{2m+1+2\sqrt{m(m+1)}} < \frac{1}{4}.$$

Ngoài ra, $b_{m(m+1)} \to \frac{1}{4}$ khi $m \to +\infty$.

• Nếu $\alpha = \frac{1}{4}$, thì dãy con $(b_{m(m+1)})_m$ hội tụ về $\frac{1}{4}$.
• Nếu $0 \le \alpha < \frac{1}{4}$ thì tồn tại $m_0$ sao cho với mọi $m \ge m_0$ thì $b_{m^2} \le \alpha < b_{m(m+1)}$. Lấy chỉ số $n_m \in \{m^2, m^2+1,\ldots,m(m+1)-1\}$ sao cho $b_{n_m} \le \alpha < b_{n_m+1}$. Ta có $$|b_{n_m} - \alpha| = \alpha - b_{n_m} < b_{n_m+1} - b_{n_m} = g_m(n_m+1) - g_m(n_m).$$
  Theo định lý giá trị trung bình, $$g_m(n_m+1) - g_m(n_m) = g_m'(x_m) = \frac{m}{2\sqrt{x_m}} + \frac{3\sqrt{x_m}}{2m} - 2$$ với $x_m \in (n_m,n_m+1)$ nào đó. Mà $m^2 \le n_m < x_m < n_m + 1 \le m(m+1)$ nên dễ thấy $\lim_{m \to +\infty}\frac{\sqrt{x_m}}{m} = 1$, suy ra $\lim_{m \to +\infty}g'_m(x_m) = \frac{1}{2} + \frac{3}{2} - 1 = 0$, từ đó ta có $\lim_{m \to +\infty}|b_{n_m} - \alpha| = 0$, hay dãy $(b_{n_m})_{m \ge m_0}$ hội tụ về $\alpha$.

Khi đổi chỗ hai hàng $i$ và $i'$, xét các trường hợp sau.

1. Nếu $i, i' \in \{i_1,\ldots,i_r\}$ thì định thức $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ đổi dấu, vì thế vẫn bằng $0$.
2. Nếu $i \in \{i_1,\ldots,i_r\}$ và $i' \notin \{i_1,\ldots,i_r\}$. Ta có thể giả sử chẳng hạn $i = i_1$. Khi đó định thức $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ trở thành $A^{i',\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$, đây là một định thức con cỡ $r+1$ của ma trận $A$ ban đầu, nên vẫn bằng $0$ theo giả thiết rằng tất cả định thức con cỡ $r+1$ của $A$ đều bằng $0$.
3. Trường hợp $i \notin \{i_1,\ldots,i_r\}$ và $i' \in \{i_1,\ldots,i_r\}$ tương tự.
4. Nếu $i, i' \notin \{i_1,\ldots,i_r\}$ thì định thức $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ không đổi, vì thế vẫn bằng $0$.

Mình lấy $A$ là ma trân vuông cỡ $n$. Với $i_1,\ldots,i_r$ và $j_1,\ldots,j_r$ là hai bộ $r$ chỉ số (không nhất thiết đôi một phân biệt), ta ký hiệu

$$A^{i_1,\ldots,i_r}_{j_1,\ldots,j_r}$$

là định thức của ma trận cỡ $r \times r$ tạo bởi lấy các phần thử trên các hàng thứ $i_1,\ldots,i_r$ của $A$ và các cột thứ $j_1,\ldots,j_r$ của $A$.

Giả sử $A$ có hạng $r$, thế thì mọi định thức con cỡ $r+1$ của $A$ đều bằng $0$, và tồn tại một định thức con cỡ $r$ của $A$ khác $0$.

• Khi đổi chỗ hai hàng hoặc hai cột, rõ ràng các định thức con $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ chỉ đảo giá trị lẫn nhau, nên vẫn bằng $0$.
• Khi nhân hàng thứ $i$ với vô hướng $\lambda \neq 0$, định thức con $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ trở thành $\lambda A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ nếu $i \in \{i_1,\ldots,i_{r+1}\}$ và không đổi nếu ngược lại, trong mọi trường hợp thì vẫn bằng $0$. Tương tự cho việc nhân một cột $j$ với một vô hướng $\lambda \neq 0$.
• Khi áp dụng $H_i \leftarrow H_i + \lambda H_{i'}$ (cộng $\lambda$ lần hàng thứ $i'$ vào hàng thứ $i$, với $i \neq i'$ và $\lambda \in \mathbb{R}$), định thức con $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ không đổi nếu $i \notin \{i_1,\ldots,i_{r+1}\}$. Trong trường hợp $i \in \{i_1,\ldots,i_{r+1}\}$, ta có thể giả sử $i = i_1$ chẳng hạn, thế thì định thức $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ trở thành $A^{i_1,\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}} + \lambda A^{i',\ldots,i_{r+1}}_{j_1,\ldots,j_{r+1}}$ qua phép biến đổi này, và vì thế vẫn bằng $0$. Tương tự cho các phép biến đổi cột $C_j \leftarrow C_j + \lambda C_{j'}$.

Vậy ta đã chứng minh nếu $A$ có hạng $r$ thì sau các phép biến đổi sơ cấp, các định thức con cấp $r+1$ cũng $A$ đều bằng $0$.

Ta còn phải chỉ ra rằng $A$ có một định thức con cấp $r$ khác $0$. Giả sử ban đầu $A$ có một định thức con cấp $r$ khác $0$ là $A^{i_1,\ldots,i_r}_{j_1,\ldots,j_r}$.

• Khi đổi chỗ hai hàng $i$ và $i'$, có thể xảy ra các trường hợp $i, i' \in \{i_1,\ldots,i_r\}$ (khi đó $A^{i_1,\ldots,i_r}_{j_1,\ldots,j_r}$ đổi dấu, vì thế vẫn khác $0$), hoặc $i \in \{i_1,\ldots,i_r\}$ và $i' \notin \{i_1,\ldots,i_r\}$, (khi đó $A^{i_1,\ldots,i_r}_{j_1,\ldots,j_r}$ sẽ khác $0$ khi thay $i$ bởi $i'$), hoặc $i \notin \{i_1,\ldots,i_r\}$ và $i' \in \{i_1,\ldots,i_r\}$ (tương tự), hoặc $i, i' \notin \{i_1,\ldots,i_r\}$ (khi đó $A^{i_1,\ldots,i_r}_{j_1,\ldots,j_r}$ không đổi, vì thế vẫn khác $0$). Tương tự khi đổi chỗ hai cột $j$ và $j'$.
• Khi nhân hàng thứ $i$ với vô hướng $\lambda \neq 0$, định thức con $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ trở thành $\lambda A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ nếu $i \in \{i_1,\ldots,i_{r}\}$ và không đổi nếu ngược lại, trong mọi trường hợp thì vẫn khác $0$. Tương tự cho việc nhân một cột $j$ với một vô hướng $\lambda \neq 0$.
• Khi áp dụng $H_i \leftarrow H_i + \lambda H_{i'}$, thì rắc rối hơn một chút.

1. Nếu $i \notin \{i_1,\ldots,i_r\}$ thì $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ không đổi, nên vẫn khác $0$.
2. Nếu $i, i' \in \{i_1,\ldots,i_r\}$ thì $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ được cộng thêm một định thức mới với hai hàng bằng nhau (thứ $i$ và thứ $i'$), nên không đổi, nên vẫn khác $0$.
3. Nếu $i \in \{i_1,\ldots,i_r\}$ và $i' \notin \{i_1,\ldots,i_r\}$. Ta giả sử chẳng hạn $i = i_1$, thế thì $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ trở thành $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}} + \lambda A^{i',\ldots,i_{r}}_{j_1,\ldots,j_{r}}$. Nếu $A^{i',\ldots,i_{r}}_{j_1,\ldots,j_{r}} = 0$ thì $A^{i_1,\ldots,i_{r}}_{j_1,\ldots,j_{r}}$ không đổi, nên vẫn khác $0$. Nếu $A^{i',\ldots,i_{r}}_{j_1,\ldots,j_{r}} \neq 0$, nhân xét rằng đây là một định thức con cấp $r$ khác $0$ của ma trận mới thu được sau khi áp dụng $H_i \leftarrow H_i + \lambda H_{i'}$ (vì phép biến đổi này chỉ thay đổi hàng $i$, trong khi $i \notin \{i',i_2,\ldots,i_r\}$.

Vậy ma trận mới thu được vẫn có một định thức con cấp $r$ khác $0$ trong mọi trường hợp. Tương tự cho phép biến đổi cột $C_j \leftarrow C_j + \lambda C_{j'}$.

Bài hay, bump lên cho các bạn học sinh làm.

Để áp dụng suy luận như trên, bạn phải tìm một khoảng ổn định của $f$, nghĩa là một khoảng/đoạn $I$ sao cho với mọi $t \in I$ thì $f(t) \in I$.

Sau đó khi bạn có $x_0 \in I$ thì bằng quy nạp sẽ có $x_n \in I$ với mọi $n$.

Tiếp theo, nếu $f$ đồng biến trên $I$ thì dãy sẽ tăng hoặc giảm, tùy theo $x_1 \ge x_0$ hay $x_1 \le x_0$.

Nếu $x_1 \ge x_0$ thì $f(x_1) \ge f(x_0)$ vì $f$ đồng biến, hay $x_2 \ge x_1$. Tiếp tục, ta có $x_3 \ge x_2$... bằng quy nạp thì $x_{n+1} \ge x_n$ với mọi $n$, hay dãy $(x_n)$ tăng.

Tương tự, nếu $x_1 \le x_0$ thì dãy $(x_n)$ giảm.

Cần nói thêm là bài làm của bạn pcoVietnam2 ở trên là chưa chặt chẽ ở đoạn này:

"$f$ đồng biến trên $\mathbb{R}$."

 

Kết luận này là sai, $f$ không xác định tại điểm điểm $\frac{4}{3}$. Ta chỉ có $f'(t) \ge 0$ với $t \in (-\infty, \frac{4}{3})$ và $t \in (\frac{4}{3},+\infty)$, nghĩa là $f$ chỉ đồng biến trên các khoảng $(-\infty, \frac{4}{3})$ và $(\frac{4}{3},+\infty)$ mà thôi.

Xin được gửi các thành viên của diễn đàn bài viết của mình về sự liên hệ giữa lý thuyết số và lý thuyết nút:

"Tôpô số học: số nguyên tố giống nút như thế nào?"

https://drive.google...?usp=share_link

Có.

Chứng minh: Xét số thực $x > N$ tùy ý.

1. Bằng quy nạp, ta chứng minh được rằng $f(nx) = nf(x)$ với mọi $n \in \mathbb{N}^\ast$.
2. Với $q$ là số hữu tỉ, $q > 1$, ta viết $q = \frac{m}{n}$ với $m, n \in \mathbb{N}^\ast$.
   Thế thì $mf(x) = f(mx) = f(nqx) = nf(qx)$ (vì $qx > N$), suy ra $f(qx) = \frac{m}{n}f(x) = qf(x)$.
3. Với $r$ là số thực, $r > 1$, chọn hai số hữu tỉ $q,q'$ sao cho $1 < q < r < q'$.
   Lấy $n \in \mathbb{N}^\ast$ đủ lớn sao cho $n(r - q) > 1$ và $n(q' - r) > 1$.
   Thế thì $nrx - nqx > x > N$ và $nq'x - nrx > x > N$.
   Suy ra $nf(rx) = f(nrx) = f(nrx - nqx) + f(nqx) > f(nqx) = nf(qx)$, nên $f(rx) > f(qx) = qf(x)$.
   Tương tự, $nf(rx) = f(nrx) < f(nrx) + f(nq'x - nrx) = f(nq'x) = nf(q'x)$, nên $f(rx) < q'f(x)$.
   Vậy $qf(x) < f(rx) < q'f(x)$.
   Vì $q$ và $q'$ có thể lấy gần $r$ một cách tùy ý nên từ bất đẳng thức trên ta có $f(rx) = rf(x)$.

Vậy $f(rx) = rf(x)$ với mọi $r \ge 1$ và $x > N$.
Nói riêng, chẳng hạn lấy $T = N+1$ và đặt $a = \frac{f(T)}{T}$. Thế thì với mọi $x > T$, ta có
$$f(x) = f\left(\frac{x}{T}\cdot T\right) = \frac{x}{T}f(T) = ax.$$

THÔNG TIN CHUNG

• Bài viết gốc: Infinity Category Theory Offers a Bird’s-Eye View of Mathematics, đăng trên Scientific American, Volume 325, Issue 4, October 2021. https://www.scientif...f-mathematics1/
• Tác giả: Giáo sư Emily Riehl, Johns Hopkins University, chuyên gia về lý thuyết phạm trù bậc cao và lý thuyết đồng luân, các công trình của cô liên quan đến phạm trù mô hình và nền tảng của lý thuyết phạm trù vô cực.
• Hình vẽ: Họa sĩ Matteo Farinella.
• Người dịch: Nguyễn Mạnh Linh, Université Paris-Saclay.

Với “vũ khí đầy mình”, tôi không kìm được mà lại gần người đàn ông trên đường. Đúng như dự đoán, nỗ lực giải thích, rằng vì sao tôi biết bài toán này không có lời giải, đã không đi tới đâu cả. Ngược lại, người đàn ông tuyên bố rằng những gì được dạy đã khiến tôi trở nên bảo thủ và không thể “mở mang cái đầu ra”. Sau cùng, bạn gái đã kéo được tôi khỏi cuộc tranh cãi và chúng tôi tiếp tục đi.

 

Nhưng vẫn còn đó một câu hỏi thú vị: Tại sao tôi, một đứa sinh viên năm ba vắt mũi chưa sạch, lại có thể học được cách dễ dàng thao túng các hệ thống số trừu tượng như các trường Galois chỉ trong vài tuần? Phần cuối của lớp học đó gồm nhóm đối xứng, vành đa thức và các cấu trúc liên quan, những thứ có lẽ sẽ làm đau đầu cả những người khổng lồ như Isaac Newton, Gottfried Leibniz, Leonhard Euler hay Carl Friedrich Gauss. Tại sao các nhà toán học lại có thể dạy cho các thế hệ sinh viên sau những khám phá làm kinh động cả những chuyên gia ở thế hệ trước?

 

PHẠM TRÙ

Giống như nhiều đồng nghiệp của mình, tôi bị toán học lôi cuốn phần vì trí nhớ tệ của mình. Điều này có thể làm nhiều người bối rối khi họ nhớ rằng môn toán ở phổ thông là một mớ công thức phải thuộc — các đẳng thức lượng giác chẳng hạn. Nhưng tôi lại thấy chúng rất dễ chịu vì hầu hết những công thức thường dùy đều có thể rút ra từ $\sin^2 \theta + \cos^2 \theta = 1$, đẳng thức mà tự thân nó có một kiến giải hình học tao nhã: đó chỉ là hệ quả trực tiếp của định lý Pythagore cho tam giác vuông với cạnh huyền bằng 1 và một góc nhọn bằng $\theta$.

Một ý tưởng toán học nghe có vẻ mâu thuẫn là đơn giản hóa bằng cách trừu tượng hóa. Như Eugenia Cheng đã viết trong “The Art of Logic in an Illogical World”(Nghệ thuật của logic trong một thế giới phi logic), “một trong những sức mạnh của trừu tượng hóa là nhiều bối cảnh khác nhau trở nên giống nhau khi bạn quên đi một số chi tiết.”Đại số hiện đại được tạo ra đầu thế kỷ XX khi các nhà toán học quyết định thống nhất nghiên cứu của họ trên nhiều ví dụ khác nhau về các cấu trúc đại số xuất hiện khi xem xét nghiệm của các hệ phương trình đa thức hay các cấu hình trong mặt phẳng. Để liên kết việc tìm hiểu các cấu trúc này, họ xác định các “tiên đề” mô tả những tính chất chung của chúng. Nhóm, vành và trường đã được đưa vào thế giới toán học, cùng ý tưởng rằng một đối tượng toán học có thể được mô tả bằng những tính chất nó có và được khám phá một cách “trừu tượng”, không phụ thuộc vào bối cảnh của những ví dụ hay xây dựng cụ thể.

 

John Horton Conway đã có một suy nghĩ nổi tiếng về bản thể luận kỳ lạ của các sự vật toán học: “Chúng chắc chắn có tồn tại, nhưng bạn không thể động chạm gì mà chỉ có thể nghĩ về chúng. Điều này thật đáng kinh ngạc, và tôi vẫn chưa hiểu, dù đã là nhà toán học suốt cuộc đời mình. Rằng làm thế nào một sự vật có thể ở đó mà lại không thực sự ở đó?'”

 

Nhưng thế giới của các đối tượng toán học tồn-tại-mà-không-thực-sự-ở-đó này có một vấn đề: Nó quá lớn cho bất kỳ ai để có thể hiểu được. Ngay trong đại số thôi đã có quá nhiều sự vật toán học để nghiên cứu, nhưng lại có quá ít thời gian để thể có thể thấy thấy cả đều hợp lý. Vào khoảng thế kỷ XX, các nhà toán học bắt đầu nghiên cứu đại số phổ dụng,  gồm một “tập hợp”, có thể là một họ những phép đối xứng, những con số trong một hệ thống hoặc thứ gì đó hoàn toàn khác, cùng một số phép toán — chẳng hạn như phép cộng và phép nhân — thỏa mãn một loạt các tiên đề liên quan như tính kết hợp, tính giao hoán hay tính phân phối. Với những điều chỉnh khác nhau như: “Phép toán được định nghĩa cục bộ hay toàn cục?”, “Nó có khả nghịch không?”, người ta thu được những cấu trúc đại số cơ bản: nhóm, vành và trường. Nhưng toán học thì không bị hạn chế bởi những điều chỉnh này, điều này cho thấy một phần rất nhỏ so với số lượng vô hạn các khả năng có thể xảy ra.

 

ĐỐI XỨNG

Các tầng trừu tượng, từ những cấu trúc toán học cụ thể đến những hệ tiên đề và sau đó là các vật trong phạm trù, mở ra một thách thức mới: sự “như nhau” giữa một vật và một vật khác không còn rõ ràng nữa. Chẳng hạn, một nhóm, đối tượng toán học được cho bởi một họ trừu tượng các phép đối xứng mà các phần tử của nó được Amie Wilkinson (Đại học Chicago) mô tả như những “chuyển động” lật hoặc xoay một đối tượng để đưa nó về trạng thái gần giống như ban đầu.

Ta có thể định nghĩa đẳng cấu trong bất kỳ phạm trù nào, cho phép ta chuyển khái niệm này giữa các ngữ cảnh toán học khác nhau. Một đẳng cấu giữa hai vật $A$ và $B$ trong một phạm trù được cho bởi một cặp biến đổi $f: A \to B$ và $g: B \to A$ với sao cho các phép biến đổi hợp thành $g \circ f$ và $f \circ g$ lần lượt là các biến đổi đồng nhất $\mathbf{1}_A$ và $\mathbf{1}_B$. Trong phạm trù các không gian tôpô, khái niệm đẳng cấu được mô tả bởi một cặp hàm liên tục nghịch đảo lẫn nhau. Chẳng hạn, có một phép biến dạng liên tục cho phép bạn biến đổi một chiếc bánh vòng (chưa nướng) thành hình dạng như tách cà phê: lỗ ở giữa chiếc bánh vòng trở thành quai cầm, và phần cốc được tạo thành bằng cách dùng ngón tay ép. (Để phép biến dạng là liên tục, bạn không được xé rách chiếc bánh, đó là lí do vì sao không nên nướng bánh trước khi làm trò này.)

 

Ví dụ này dẫn đến câu đùa rằng nhà tôpô học không thể phân biệt giữa tách cà phê và chiếc bánh vòng: với tư cách là các không gian trừu tượng, hai đối tượng này giống nhau. Trên thực tế, nhiều nhà tôpô học có khả năng phân biệt còn tệ hơn thế nữa kia; đó là vì họ đã sử dụng một quy ước linh hoạt hơn nhiều để mô tả tình huống khi hai không gian là “như nhau”, họ đồng nhất hai không gian bất kỳ mà chỉ “tương đương đồng luân” với nhau thôi. Thuật ngữ trên là khái niệm đẳng cấu trong một phạm trù kỳ lạ hơn, phạm trù đồng luân của các không gian. Một tương đương đồng luân là một kiểu biến dạng liên tục khác, nhưng lúc này bạn được phép dính hai điểm phân biệt với nhau. Chẳng hạn, tưởng tượng rằng bạn bắt đầu với chiếc quần jean và thu gọn chiều dài của hai ống quần đến khi bạn thu được chiếc quần lọt khe, một “không gian” khác mà cấu trúc tôpô về cơ bản là không đổi —nó vẫn có hai lỗ để cho chân vào, dù hai ống quần ($2$-chiều) ban đầu đã bị rút thành hai vòng dây ($1$-chiều).

 

PHẠM TRÙ VÔ CỰC

Ưu thế then chốt của phỏng nhóm cơ bản là tính “hàm tử”, nghĩa là mọi hàm liên tục $f: X \to Y$ giữa hai không gian tôpô cho ta một phép biến đổi $\pi_1 f: \pi_1 X \to \pi_1 Y$ giữa hai phỏng nhóm cơ bản. Phép biến đổi này tôn trọng phép hợp thành và đồng nhất của đường, nghĩa là $\pi_1(g \circ f) = \pi_1 g \circ \pi_1 f$ và $\pi_1(\mathbf{1}_x) = \mathbf{1}_{\pi_1 x}$. Hai tính chất này, gọi chung là “tính hàm tử”, gợi ý rằng phỏng nhóm cơ bản giữ được những tính chất cốt lõi của không gian tôpô. Nói riêng, nếu hai không gian không tương đương đồng luân thì phỏng nhóm cơ bản của chúng cũng không tương đương.

 

Dù vậy, phỏng nhóm cơ bản chưa phải là một bất biến hoàn chỉnh. Có thể dễ dàng phân biệt một đường tròn với hình tròn đặc mà đường tròn ấy bao quanh. Trong phỏng nhóm cơ bản của đường tròn, các đường giữa hai điểm cho trước, sai khác biến dạng liên tục (đồng luân), được gán với các số nguyên, chỉ số vòng mà đường này quay quanh đường tròn, với dấu $+$ hoặc $-$ chỉ chiều thuận hoặc ngược kim đồng hồ. Ngược lại, trong phỏng nhóm cơ bản của hình tròn, chỉ có duy nhất (sai khác đồng luân) một đường giữa bất kỳ cặp điểm nào. Phỏng nhóm cơ bản của phần bề mặt của quả bóng, hay một mặt cầu theo ngôn ngữ tôpô, cũng thỏa mãn chính chất này: tồn tại duy nhất, sai khác đồng luân, một đường giữa hai điểm bất kỳ.

 

 

 

 

CHÂN TRỜI TƯƠNG LAI

 

Dẫu vậy, kinh nghiệm lịch sử cho thấy rằng phần lớn những kiến thức toán học mới lạ nhất hôm nay sẽ dần trở nên đủ dễ để dạy cho sinh viên toán ngài mai. Sẽ rất vui khi được quan sát, với tư cách là một người nghiên cứu $\infty$-phạm trù, cách mà nó có thể được đơn giản hóa đi. Chẳng hạn như một mẹo nhỏ về ngôn ngữ —một phiên bản siêu cấp của từ “the” trong phạm trù —có thể khiến cho sinh viên ở cuối thế kỷ XXI hiểu $\infty$-phạm trù một cách dễ dàng như phạm trù thông thường ngày nay. Tiên đề then chốt của lý thuyết phạm trù thông thường là sự tồn tại duy nhất của một phép biến đổi hợp thành $g \circ f: X \to Z$ với mỗi cặp biến đổi $f: X \to Y$ và $g: Y \to Z$, được chọn ra từ tập các phép biến đổi từ $X$ vào $Z$. Trái lại, trong một $\infty$-phạm trù, có một không gian các mũi tên từ $X$ vào $Z$, thứ mà trong $\infty$-phỏng nhóm cơ bản có thể hiểu là “không gian đường”. Phiên bản đúng của tính hợp thành duy nhất trong phạm trù thông thường là mệnh đề: trong một $\infty$-phạm trù, không gian các hợp thành là “co rút được”, nghĩa là mỗi điểm của nó đều có thể suy sụp một cách liên tục qua một vụ nổ “Big Bang ngược” về một điểm gốc duy nhất.

 

Chú ý rằng tính co rút được không suy ra rằng có duy nhất một hợp thành: thật vậy, ta đã thấy rằng trong $\infty$-phỏng nhóm cơ bản, có thể có rất nhiều đường hợp thành. Nhưng tính co rút được đảm bảo rằng hai đường hợp thành luôn đồng luân, và hai phép đồng luân bất kỳ giữa hai đường hợp thành luôn liên kết với nhau bởi một đồng luân bậc cao, và cứ như vậy.

 

4. Liên hợp Quillen

Mệnh đề - Định nghĩa 4.1. Cho $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một cặp hàm tử liên hợp giữa hai phạm trù mô hình. Khi đó 4 khẳng định sau đây tương đương

1. $F$ bảo toàn đối phân thớ và đối phân thớ acyclic.
2. $G$ bảo toàn phân thớ và phân thớ acyclic.
3. $F$ bảo toàn đối phân thớ và $G$ bảo toàn phân thớ.
4. $F$ bảo toàn đối phân thớ acyclic và $G$ bảo toàn phân thớ acyclic.

Khi các điều kiện trên được thỏa mãn, ta nói $F$ và $G$ là một cặp liên hợp Quillen.

Chứng minh. Nhắc lại (Mệnh đề 2.2) rằng một cấu xạ là một đối phân thớ (tương ứng, đối phân thớ acyclic) khi và chỉ khi nó có tính chất nâng trái đối với mọi phân thớ acyclic (tương ứng, phân thớ). Một cách đối ngẫu, một cấu xạ là một phân thớ (tương ứng, phân thớ acyclic) khi và chỉ khi nó có tính chất nâng phải đối với mọi đối phân thớ acyclic (tương ứng, đối phân thớ). 

Ta chứng minh rằng nếu $F$ bảo toàn đối phân thớ thì $G$ bảo toàn phân thớ acyclic. Thật vậy, cho $p: X \tilde{\twoheadrightarrow} Y$ là một phân thớ acyclic trong $\mathbb{N}$. Ta chứng minh rằng $Gp: GX \to GY$ là một phân thớ acyclic trong $\mathbf{N}$. Xét $i: A \hookrightarrow B$ là một đối phân thớ tùy ý (trong $\mathbf{N}$). Vì $Fi$ là một đối phân thớ nên theo (MC4), tồn tại mũi tên đứt làm giao hoán biểu đồ với các mũi tên liền

Sau khi lấy liên hợp, ta thu được mũi tên đứt làm giao hoán biểu đồ với các mũi tên liền

Vậy $i \perp Gp$. Suy ra $Gp$ là một đối phân thớ acyclic.

Tương tự, nếu $F$ bảo toàn đối phân thớ acyclic thì $G$ bảo toàn phân thớ. Một cách đối ngẫu, nếu $G$ bảo toàn phân thớ (tương ứng, phân thớ acyclic) thì $F$ bảo toàn đối phân thớ acyclic (tương ứng, đối phân thớ). Từ các kết quả này, ta dễ thấy rằng 4 điều kiện đã cho tương đương. $\square$

Nhận xét rằng nếu $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một cặp liên hợp Quillen thì $F$ bảo toàn vật đối phân thớ (tương ứng, $G$ bảo toàn vật phân thớ). Thật vậy $F \varnothing = \varnothing$ (vì $F$ bảo toàn đối giới hạn) và $G \ast = \ast$ (vì $G$ bảo toàn giới hạn). Hơn nữa, theo Bổ đề Brown (xem chứng minh của Mệnh đề 3.6), $F$ bảo toàn tương đương yếu giữa hai vật đối phân thớ và $G$ bảo toàn tương đương yếu giữa hai vật phân thớ.

Ví dụ 4.2. Cho $f: R \to S$ là một đồng cấu vành. Khi đó $-\otimes_R S: \mathbf{Ch}_{\ge 0} (R) \leftrightarrows \mathbf{Ch}_{\ge 0}(S): f^\ast$ là một cặp liên hợp Quillen trên mô hình xạ ảnh.

Với $\mathbf{M}$ là một phạm trù mô hình, ta ký hiệu bởi $\lambda: \mathbf{M} \to \mathbf{Ho}(\mathbf{M})$ hàm tử địa phương hóa.

Định nghĩa. Cho $\mathbf{H}$ là một phạm trù tùy ý và $F: \mathbf{M} \to \mathbf{H}$ là một hàm tử.

• Một hàm tử dẫn xuất trái của $F$ gồm một hàm tử $\mathbb{L}F: \mathbf{Ho}(\mathbf{M}) \to H$ và một biến đổi tự nhiên $\alpha: \mathbb{L} F \circ \lambda \Rightarrow F$ sao cho: với mọi hàm tử $G: \mathbf{Ho}(\mathbf{M}) \to H$ và mọi biến đổi tự nhiên $\beta: G \lambda \Rightarrow F$, tồn tại duy nhất biến đổi tự nhiên $\theta: G \Rightarrow \mathbb{L} F$ (lạm dụng ký hiệu, ta cũng coi nó như một biến đổi tự nhiên $G \lambda \Rightarrow \mathbb{L}F \circ \lambda$) sao cho ta có $\beta = \alpha \circ \theta: G\lambda \Rightarrow F$.
• Một hàm tử dẫn xuất phải của $F$ gồm một hàm tử $\mathbb{R}F: \mathbf{Ho}(\mathbf{M}) \to H$ và một biến đổi tự nhiên $\varepsilon: F \Rightarrow \mathbb{R} F \circ \lambda$ sao cho: với mọi hàm tử $G: \mathbf{Ho}(\mathbf{M}) \to H$ và mọi biến đổi tự nhiên $\phi: F \Rightarrow G \lambda$, tồn tại duy nhất biến đổi tự nhiên $\phi: \mathbb{R} F  \Rightarrow  G$ sao cho ta có $\phi = \theta \circ \varepsilon: F \Rightarrow G\lambda$.

Hàm tử liên hợp (trái hoặc phải) của một hàm tử, nếu tồn tại, là duy nhất sai khác đẳng cấu tự nhiên.

Nhắc lại rằng ta có hàm tử giải đối phân thớ $Q: \mathbf{M} \to \mathbf{M}$ cùng biến đổi tự nhiên $p: Q \Rightarrow \mathbf{1}_{\mathbf{M}}$. Hơn nữa, $Q$ bảo toàn tương đương yếu (dùng (MC2)).

Mệnh đề 4.3. Nếu $F$ biến đối phân thớ acyclic giữa hai vật đối phân thớ (tương ứng, phân thớ acyclic giữa hai vật phân thớ) thành đẳng cấu thì $F$ có dẫn xuất trái (tương ứng, dẫn xuất phải). Nói riêng, nếu $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một cặp liên hợp Quillen thì $F$ có dẫn xuất trái và $G$ có dẫn xuất phải.

Chứng minh. Ta chỉ cần chứng minh ý thứ nhất. Xét cấu trúc mô hình trên $\mathbf{H}$ trong đó tương đương yếu là đẳng cấu, và mọi cấu xạ đều là phân thớ cũng như đối phân thớ. Theo Bổ đề Brown, $F$ biến tương đương yếu giữa hai vật đối phân thớ thành đẳng cấu. Do đó $FQ$ phân tích qua $\mathbf{Ho}(\mathbf{M})$, nghĩa là $FQ = \mathbb{L} F \circ \lambda$ với hàm tử $\mathbb{L} F: \mathbf{Ho}(\mathbf{M}) \to \mathbf{H}$ nào đó. Trên các vật, ta có $\mathbb{L} F = FQ X$. Ngoài ra, $p: Q \Rightarrow \mathbf{1}_{\mathbf{M}}$ cảm sinh biến đổi tự nhiên $\alpha: \mathbb{L}F \circ \lambda = FQ \Rightarrow F$.

Ta chứng minh rằng cặp $(\mathbb{L}F, \alpha)$ vừa xây dựng thỏa mãn tính chất phổ dụng của hàm tử liên hợp trái. Thật vậy, cho $G: \mathbf{Ho}(\mathbf{M}) \to \mathbf{H}$ là một hàm tử và $\beta: G\lambda \Rightarrow F$ là một biến đổi tự nhiên. Với mỗi vật $X$ trong $\mathbf{M}$, tương đương yếu $p_X: QX \tilde{\twoheadrightarrow} X$ trở thành đẳng cấu $\lambda p_X$ trong $\mathbf{Ho}(\mathbf{M})$, nên $G\lambda p_X: GQX \cong GX$. Đặt $\theta_X = \beta_{QX} \circ G \lambda p_X^{-1}: GX \to F QX$. Thế thì $\theta$ là một biến đổi tự nhiên $G \Rightarrow \mathbb{L}F$, hơn nữa vì $\alpha_X \beta_{QX} = \beta_X \circ Gp_X$ nên $\beta_X = \alpha_X \theta_X$, hay $\beta = \alpha \circ \theta$.

Ta chỉ ra rằng biến đổi tự nhiên $\theta$ như vậy là duy nhất. Thật vậy, nếu $\theta'$ là một biến đổi tự nhiên khác như vậy thì với mọi vật $X$, ta có $\beta_{QX} = \alpha_{QX} \theta'_{QX}$. Xét hình lập phương giao hoán

trong đó mọi vật trừ $X$ đều là vật đối phân thớ, và mọi mũi tên đều là tương đương yếu. Áp dụng $F$, ta thu được các đẳng cấu, trừ ba mũi tên $Fp_X$. Tính giao hoán của mặt trên cho ta $FQQp_X = FQp_X$, mặt trái cho ta $FQp_X = Fp_{QQX}$. Từ đó $FQQp_X = Fp_{QQX}$, và tính giao hoán của mặt sau cho ta $Fp_{QX} = FQp_X = \alpha_X$. Cuối cùng, tính tự nhiên của $\theta'$ cho ta $$\theta'_X \circ G \lambda p_X = FQp_X \circ \theta'_{QX} = \alpha_X \theta'_{QX} = \beta_{QX} = \theta_X \circ G\lambda p_X,$$ suy ra $\theta'_X = \theta_X$ (vì $G\lambda p_X$ là một đẳng cấu). $\square$

Định nghĩa. Cho $F: \mathbf{M} \to \mathbf{N}$ là một hàm tử giữa hai phạm trù mô hình.

• Một hàm tử dẫn xuất trái toàn phần của $F$ là một hàm tử dẫn xuất trái của $\lambda F: \mathbf{M} \to \mathbf{Ho}(\mathbf{N})$.
• Một hàm tử dẫn xuất phải toàn phần của $F$ là một hàm tử dẫn xuất phải của $\lambda F: \mathbf{M} \to \mathbf{Ho}(\mathbf{N})$.

Lạm dụng ký hiệu, ta vẫn viết $\mathbb{L}F: \mathbf{Ho}(\mathbf{M}) \to \mathbf{Ho}(\mathbf{N})$ (tương ứng, $\mathbb{R}F: \mathbf{Ho}(\mathbf{M}) \to \mathbf{Ho}(\mathbf{N})$) để chỉ hàm tử dẫn xuất trái (tương ứng, phải) toàn phần. Theo định nghĩa, ta có các biến đổi tự nhiên $\mathbb{L}F \circ \lambda \Rightarrow \lambda F$ và $\lambda F \Rightarrow \mathbb{R}F$. Từ đó, nếu $\mathbf{M} \xrightarrow{F} \mathbf{N} \xrightarrow{G} \mathbf{P}$ là các hàm tử sao cho $F$, $G$ và $G \circ F$ đều có dẫn xuất trái (tương ứng, phải) thì ta có biến đổi tự nhiên $\mathbb{L} G \circ \mathbb{L}F \Rightarrow \mathbb{L}(GF)$.

Định lý 4.4. Cho $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một cặp liên hợp Quillen giữa hai phạm trù mô hình, khi đó $\mathbb{L} F: \mathbf{Ho}(\mathbf{M}) \leftrightarrows \mathbf{Ho}(\mathbf{N}) :\mathbb{R}G$ là một cặp liên hợp.

Chứng minh. Từ chứng minh của Mệnh đề 4.3, ta có $\mathbb{L}FA = FQA$ và $\mathbb{R}GX = GRX$, trong đó $Q: \mathbf{M} \to \mathbf{M}$ và $R: \mathbf{N} \to \mathbf{N}$ lần lượt là hàm tử giải đối phân thớ và giải phân thớ. Ta có song ánh tự nhiên $$\text{Hom}_{\mathbf{N}}(FQA,RX) \cong \text{Hom}_{\mathbf{M}}(QA,GRX).$$

Chú ý rằng $FQA$ là một vật đối phân thớ và $QRX$ là một vật phân thớ. Ta chỉ ra rằng song ánh trên cảm sinh song ánh sau khi lấy đồng luân. Thật vậy, giả sử $f,g: FQA \to RX$ là hai cấu xạ đồng luân. Xét $RY \tilde{\rightarrow} P \twoheadrightarrow RY \times RY$ là một vật đường và $H: FQA \to P$ là một đồng luân phải giữa $f$ và $g$. Vì $G$ bảo toàn phân thớ và giới hạn, ta thu được phân tích $GRY \to GP \twoheadrightarrow GRY \times GRY$ của cấu xạ đường chéo. Mà $RY$ là một vật phân thớ (nên $P$ cũng vậy) và $G$ bảo toàn tương đương yếu giữa các vật phân thớ (Bổ đề Brown) nên phân tích $GRY \tilde{\rightarrow} GP \twoheadrightarrow GRY \times GRY$ là một vật đường của $GRY$. Lấy liên hợp của $H: FQA \to P$, ta thu được $H': QA \to GP$, đây là một đồng luân phải giữa liên hợp của $f$ và $g$. Một cách đối ngẫu, nếu ta có hai cấu xạ đồng luân $QA \to GRX$ thì liên hợp của chúng cũng là hai cấu xạ đồng luân $FQA \to RX$. Vậy ta có song ánh $$[FQA,RX] = \text{Hom}_{\mathbf{N}}(FQA,RX)/\simeq \cong \text{Hom}_{\mathbf{M}}(QA,GRX)\simeq = [QA,GRX].$$

Cuối cùng, theo Định lý cơ bản của phạm trù đồng luân (Định lý 3.17), ta có song ánh tự nhiên $$\text{Hom}_{\mathbf{Ho}(\mathbf{N})}(\mathbb{L}F(A),X) = \text{Hom}_{\mathbf{Ho}(\mathbf{N})}(FQA,X) \cong [FQA,RX] \cong [QA, GRX] \cong \text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,GRX) = \text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,\mathbb{R}G(X)).$$ $\square$

Mệnh đề 4.5. Nếu $\mathbf{M} \xrightarrow{F} \mathbf{N} \xrightarrow{G} \mathbf{P}$ là các liên hợp Quillen trái giữa các phạm trù mô hình thì biến đổi tự nhiên $\eta: \mathbb{L} G \circ \mathbb{L}F \Rightarrow \mathbb{L}(GF)$.là một đẳng cấu tự nhiên.

Chứng minh. Ta có $\mathbb{L} G (\mathbb{L}F(A)) = \mathbb{L} G(FQA) = GQFQA$, $\mathbb{L}(GF)(A) = GFQA$ (trong đó $Q$ là các hàm tử giải đối phân thớ) và $\alpha_A = \lambda Gp_{FQA}$ (trong đó $p_{FQA}: QFQA \tilde{\twoheadrightarrow} FQA$ là cấu xạ cho bởi phân tích đối phân thớ của $FQA$, và $\lambda: \mathbf{P} \to \mathbf{Ho}(\mathbf{P})$ là cấu xạ địa phương hóa). Mà $FQA$ và $QFQA$ là các vật đối phân thớ nên $Gp_{FQA}$ là một tương đương yếu, hay $\lambda Gp_{FQA}$ là một đẳng cấu trong $\mathbf{Ho}(\mathbf{P})$. $\square$

Định lý - Định nghĩa 4.6. Cho $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một cặp liên hợp Quillen giữa hai phạm trù mô hình. Lần lượt ký hiệu bởi $\eta: \mathbf{1}_{\mathbf{M}} \Rightarrow GF$ và $\varepsilon: FG \to \mathbf{1}_{\mathbf{N}}$ các biến đổi đơn vị và đối đơn vị. Các khẳng định sau tương đương.

1. Cặp liên hợp cảm sinh $\mathbb{L} F: \mathbf{Ho}(\mathbf{M}) \leftrightarrows \mathbf{Ho}(\mathbf{N}) :\mathbb{R}G$ là các tương đương phạm trù (tựa nghịch đảo lẫn nhau).
2. Với mọi vật đối phân thớ $A$ trong $\mathbf{M}$ và mọi vật phân thớ $X$ trong $\mathbf{N}$, một cấu xạ $FA \to X$ là một tương đương yếu khi và chỉ khi liên hợp $A \to GX$ của nó cũng vậy.
3. Với mọi vật đối phân thớ $A$ trong $\mathbf{M}$ và mọi vật phân thớ $X$ trong $\mathbf{N}$, các cấu xạ hợp thành $$A \xrightarrow{\eta_A} GF A \to GRFA, \qquad FQGX \to FGX \xrightarrow{\varepsilon_X} X$$ là các tương đương yếu (trong đó $Q: \mathbf{M} \to \mathbf{M}$ và $R: \mathbf{N} \to \mathbf{N}$ lần lượt là hàm tử giải đối phân thớ và giải phân thớ).

Khi các điều kiện trên được thỏa mãn, ta nói cặp $F: \mathbf{M} \leftrightarrows \mathbf{N} :G$ là một tương đương Quillen.

Chứng minh. Ta chứng minh $3. \Rightarrow 2. \Rightarrow 1.$

$3 \Rightarrow 2.$ Cho $A$ là một đối phân thớ trong $\mathbf{M}$, $X$ là một vật phân thớ trong $\mathbf{X}$ và $f: FA \to X$ là một cấu xạ. Giả sử $f$ là một tương đương yếu. Liên hợp của $f$ là $g = Gf \circ \eta_{A}: A \to GX$. Ta có biểu đồ giao hoán 

Ở đây $GX \to GRX$ và $GRFA \to GRX$ là các tương đương yếu vì $X \tilde{\hookrightarrow} RX$ và $RFA \tilde{\hookrightarrow} RX$ là các tương đương yếu giữa hai vật phân thớ (chú ý rằng $R$ bảo toàn tương đương yếu theo (MC2)). Ngoài ra, $A \to GRFA$ là một tương yếu theo giả thiết. Vì thế $g = Gf \circ \eta_A$ là một tương đương yếu theo (MC2). Một cách đối ngẫu, nếu $g$ là một tương yếu thì $f$ cũng vậy.

$2 \Rightarrow 1$, Ký hiệu $\tilde{\eta}: \mathbf{1}_{\mathbf{Ho}(\mathbf{M}} \Rightarrow \mathbb{R} G \circ \mathbb{L}F$, là biến đổi đơn vị của cặp liên hợp cảm sinh $\mathbb{L} F: \mathbf{Ho}(\mathbf{M}) \leftrightarrows \mathbf{Ho}(\mathbf{N}) :\mathbb{R}G$. Với mỗi vật $A$ trong $\mathbb{M}$, cấu xạ $\tilde{\eta}_A \in \text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A, \mathbb{R}G(\mathbb{L}F(A))) = [QA,GRFQA]$ là liên hợp của (lớp đồng luân của) cấu xạ $FQA \tilde{\hookrightarrow} RFQA$. Đây là một đối phân thớ acyclic giữa hai vật đối phân thớ ($FQA$ là một vật đối phân thớ nên $RFQA$ cũng vậy), do đó $\tilde{\eta}_A$ là lớp đồng luân của một tương đương yếu (theo giả thiết), nghĩa là một đẳng cấu. Tương tự, biến đổi đối đơn vị $\tilde{\varepsilon}: \mathbb{L} F \circ \mathbb{R}G \Rightarrow \mathbf{1}_{\mathbf{Ho}(\mathbf{N})}$ là một đẳng cấu tự nhiên.

$1 \Rightarrow 3.$ Giả sử $A$ là một vật đối phân thớ trong $\mathbf{M}$. Ta có biểu đồ giao hoán

Theo giả thiết, cấu xạ đơn vị $QA \to GRFQA$ là trở thành đẳng cấu trong phạm trù dẫn xuất, tức là một tương đương yếu. Vì $QA \to A$ là một tương đương yếu giữa hai vật đối phân thớ nên $FQA \to FA$ là một tương đương yếu, suy ra $RFQA \to RFA$ cũng vậy (theo (MC2)). Mà $RFQA$ và $RFA$ là các vật phân thớ nên $GRFQA \to GRFA$ là một tương đương yếu. Theo (MC2) thì $A \to GRFA$ là một tương đương yếu. Một cách đối ngẫu, nếu $X$ là một vật phân thớ trong $\mathbf{N}$ thì $FQGX \to X$ là một tương đương yếu. $\square$

Ví dụ 4.7. Cho $R$ là một vành. Hàm tử đồng nhất trên $\mathbf{Ch}(R)$ là một tương đương Quillen giữa mô hình xạ ảnh ở bên trái và mô hình nội xạ ở bên phải.

Ví dụ 4.8. Ở bài https://diendantoanh...g-luân-đơn-hình, ta đã xây dựng cặp liên hợp $$|-|: \mathbf{sSet} \leftrightarrows \mathbf{Top}: \text{Sing}_\bullet$$ giữa hàm tử hình học hóa trên các tập đơn hình và hàm tử phức kỳ dị. Đây là một tương đương Quillen, trong đó

• cấu trúc mô hình trên $\mathbf{sSet}$: các tương đương yếu là các ánh xạ đơn hình với hình học hóa là tương đương đồng luân yếu, các đối phân thớ là các phép bao hàm, các phân thớ là các phân thớ Kan (các ánh xạ đơn hình thỏa mãn tính chất nâng phải đối với các phép bao hàm $\Lambda^n_k \hookrightarrow \Delta^n$ của các sừng trong đơn hình chuẩn);
• cấu trúc mô hình trên $\mathbf{Top}$ là cấu trúc Quillen: các tương đương yếu là các tương đương đồng luân yếu, các đối phân thớ là rút gọn của các phép bao hàm của CW-phức suy rộng, các phân thớ là các phân thớ Serre.(Ví dụ 2.4).

Một lý thuyết toán học gồm những tiên đề và một hệ thống quy tắc suy luận. Chứng minh toán học là dùng các quy tắc suy luận để đi từ các tiên đề đến các định lý, phát biểu... Các định nghĩa dựa theo những định nghĩa đã có trước. Vì thế phải có những khái niệm nguyên thủy đầu tiên, không định nghĩa (không nói chúng là gì, nhưng chúng phải thỏa mãn những tiên đề của lý thuyết).

Hệ tiên đề được sử dụng rộng rãi trong toán học hiện nay là lý thuyết tập hợp ZFC.  Đối tượng nguyên thủy (không định nghĩa) là các tập hợp. Một khái niệm được coi là định nghĩa rõ ràng nếu nó là một tập hợp, một phần tử của một tập hợp nào đó... Hình thức hóa về cơ bản là đưa các khái niệm về lý thuyết tập hợp, sử dụng các mệnh đề toán học (gồm các toán hạng như các số 0,1, 2,..., quan hệ giữa các toán hạng như dấu =, <, >, ..., và các toán tử của logic vị từ "và", "hoặc", "$\implies$", $\iff$,... cũng như hai lượng từ của logic bậc nhất $\forall$, $\exists$.

3. Đồng luân

Cho $(\mathbf{M}, \mathscr{W}, \mathscr{C}, \mathscr{F})$ là một phạm trù mô hình. Ta mô tả lớp $\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X)$ các cấu xạ trong phạm trù đồng luân giữa hai vật $A$ và $X$. Tính huống lý tưởng nhất là khi ta có thể mô tả nó như thương của một lớp các cấu xạ trong $\mathbf{M}$ bởi một quan hệ đồng luân.

Cần chú ý rằng có hai khái niệm đồng luân đối ngẫu của nhau: đồng luân trái (trên nguồn) và đồng luân phải (trên đích). Ta định nghĩa chúng bằng cách tổng quát hóa các khái niệm không gian đường (Ví dụ 1.9) và hình trụ (Ví dụ 1.14), nhờ tiên đề phân tích (MC5).

Định nghĩa. Một hình trụ của một vật $A$ là một phân tích $A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$ của cấu xạ hiển nhiên $A \sqcup A \xrightarrow{(1_A,1_A)} A$.

Ta ký hiệu bởi $i_0,i_1: A \to C$ các thành phần của phép đối phân thớ $(i_0,i_1): A \sqcup A \hookrightarrow C$ trong phân tích trên.

Định nghĩa. Cho hai cấu xạ $f,g: A \to X$. Một phép đồng luân trái giữa $f$ và $g$ là một hình trụ $A \sqcup A \hookrightarrow{C} \tilde{\rightarrow} A$ cùng một cấu xạ $H: C \to X$ sao cho $H i_0 = f$ và $H i_1 = g$. Khi $H$ tồn tại, ta nói $f$ đồng luân trái với $g$ và ký hiệu $f \simeq_l g$.

Nhìn chung, không có một cách chọn hình trụ "chính tắc". Hai cấu xạ có thể đồng luân qua một hình trụ nào đó, nhưng không qua một hình trụ khác.

Ví dụ 3.1. Trong $\mathbf{Top}$ với mô hình Quillen, nếu $A$ là một vật đối phân thớ, ta có thể lấy $C = A \times [0,1]$, một phép đồng luân trái chính là một phép đồng luân theo nghĩa cổ điển.

Ví dụ 3.2. Cho $R$ là một vành, trong $\mathbf{Ch}(R)$ với mô hình nội xạ, xét một phức dây chuyền $A$. Ta có thể lấy phức $C$ với $C_n = A_n \oplus A_n \oplus A_{n-1}$ và vi phân $d(x,y,z) = (dx + (-1)^n z, dy - (-1)^n z, dz)$. Một phép đồng luân trái chính là một phép đồng luân dây chuyền.

Mệnh đề 3.3. Nếu $f \simeq_l g: A \to X$ thì với mọi cấu xạ $h: X \to Y$, ta có $hf \simeq_l hg: A \to Y$.

Chứng minh. Nếu $H: C \to X$ là một phép đồng luân trái giữa $f$ và $g$ thì $hH: C \to Y$ là một phép đồng luân trái giữa $hf$ và $hg$. $\square$

Bổ đề 3.4. Nếu $A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$ là một hình trụ và $A$ là một vật đối phân thớ thì $i_0,i_1: A \to C$ là các đối phân thớ acyclic.

Chứng minh. Phép nhúng thứ nhất $A \to A \sqcup A$ là một đẩy ra của đối phân thớ $\varnothing \to A$, vì thế cũng là một đối phân thớ, suy ra hợp thành $i_0: A \to A \sqcup A \to C$ cũng là một đối phân thớ. Mặt khác, hợp thành của $$A \xrightarrow{i_0} C \tilde{\rightarrow} A$$ chính là $1_A$ theo định nghĩa của cấu xạ hiển nhiên $A \sqcup A \to A$, ta biết rằng $1_A$ là một tương đương yếu (Hệ quả 2.3) nên theo (MC2) thì $i_0$ cũng là một tương đương yếu. Vậy $i_0$ là một đối phân thớ acyclic, tương tự cho $i_1$. $\square$

Mệnh đề 3.5. Nếu $A$ là một vật đối phân thớ thì $\simeq_l$ là một quan hệ tương đương trên $\text{Hom}_{\mathbf{M}}(A,X)$.

Chứng minh.

• Tính phản xạ. Cho cấu xạ $f: A \to X$. Xét một hình trụ tùy ý $A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$ (luôn tồn tại theo (MC5)). Thế thì hợp thành $H: C \tilde{\rightarrow} A \xrightarrow{f} X$ là một phép đồng luân giữa $f$ và chính nó.


• Tính đối xứng. Giả sử $f \simeq_l g$ bởi một phép đồng luân $H: C \to X$. Ta định nghĩa một hình trụ mới $A \sqcup A \cong A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$, trong đó đẳng cấu đầu tiên là phép đảo hai thành phần. Đối với hình trụ mới này, hai thành phần của phép phân thớ $ A \sqcup A \hookrightarrow C$ lần lượt là $i_1$ và $i_0$, vì thế $H$ định nghĩa một phép đồng luân trái giữa $g$ và $f$ vì $Hi_1 = g$ và $Hi_0 = f$.


• Tính truyền dẫn. Đây là chỗ ta cần dùng giả thiết $A$ là vật đối phân thớ. Giả sử $f \simeq_l g$ và $g \simeq_l h$ lần lượt bởi các phép đồng luân $H: C \to X$ và $H': C' \to X$. Ta có $Hi_1 = H'i_0' = g$ nên ta sẽ "dán" $i_1$ và $i_0'$ như sau: ký hiệu $\bar{C}$ là đẩy ra của cặp cấu xạ $$i_1: A \to C \qquad i_0': A \to C'.$$ Các hợp thành $A \xrightarrow{i_1} C \tilde{\rightarrow}A$ và $A \xrightarrow{i_0'} C' \tilde{\rightarrow} A$ đều bằng $1_A$ nên theo tính chất phổ dụng của đẩy ra, chúng cảm sinh một cấu xạ $\bar{C} \to A$. Chú ý rằng $j: C \to \bar{C}$ và $j': C' \to \bar{C}$ là các đối phân thớ acyclic (chúng là đẩy ra của $i_1$ và $i_0'$, đây là các phân thớ acyclic theo Bổ đề 3.4), nên theo (MC2) thì $\bar{C} \to A$ là một tương đương yếu. Xét cấu xạ $(ji_0, j'i_1'): A \sqcup A \to \bar{C}$, nó không nhất thiết là một phân thớ. Ta khắc phục điều này bằng cách dùng (MC5) để phân tích nó thành $A \sqcup A \tilde{\rightarrow} C'' \tilde{\rightarrow} \bar{C}$, từ đó ta có hình trụ $A \sqcup A \hookrightarrow C'' \tilde{\rightarrow} A$. Cuối cùng, vì $Hi_1 = H'i_0' = g$ nên tính chất phổ dụng của đẩy ra cho ta một cấu xạ $\bar{H}: \bar{C} \to X$ thỏa mãn $\bar{H} j = H$ và $\bar{H}j' = H'$. Nói riêng, $\bar{H}ji_0 = Hi_0 = f$ và $\bar{H}j'i_1' = H'i_1' = h$. Như vậy, hợp thành $H'': C'' \tilde{\rightarrow} \bar{C} \xrightarrow{\bar{H}} X$ là một phép đồng luân trái giữa $f$ và $h$. $\square$

Cho $A$ là một vật đối phân thớ và $h: X \to Y$ là một cấu xạ. Theo các Mệnh đề 3.3 và 3.5 thì $h$ cảm sinh một ánh xạ $$h_\ast: \text{Hom}_{\mathbf{M}}(A,X) / \simeq_l \to \text{Hom}_{\mathbf{M}}(A,Y) / \simeq_l, \qquad [f] \mapsto [hf].$$

Mệnh đề 3.6. Nếu $A$ là một vật đối phân thớ và $h: X \tilde{\twoheadrightarrow} Y$ là một phân thớ acyclic thì $h_\ast$ là một song ánh. Kết luận này vẫn đúng nếu $h$ là một tương đương yếu và $X, Y$ là các vật phân thớ.

Chứng minh. Giả sử $h$ là một phân thớ acyclic. Xét một cấu xạ $g: A \to Y$ tùy ý. Ta áp dụng (MC4) cho biểu đồ giao hoán

Thế thì tồn tại cấu xạ $f: A \to X$ sao cho $g = hf$, suy ra $h_\ast$ là một toàn ánh.

Giả sử $f,g: A \to X$ là hai cấu xạ sao cho $hf \simeq_l hg$, nghĩa là tồn tại một hình trụ $A \sqcup A \hookrightarrow C \tilde{\twoheadrightarrow} A$ và một phép đồng luân $H: C \to Y$ giữa $hf$ và $hg$. Nói cách khác, biểu đồ với các mũi tên liền dưới đây

giao hoán. Áp dụng (MC4), ta tìm được mũi tên đứt $K$, đó là một phép đồng luân giữa $f$ và $g$. Vậy $h_\ast$ là một đơn ánh.

Tiếp theo, xét trường hợp $X, Y$ là các vật phân thớ và $h$ là một tương đương yếu. Ta áp dụng

Bổ đề Brown. Cho $F: \mathbf{M} \to \mathbf{N}$ là một cấu xạ giữa hai phạm trù mô hình.

• Nếu $F$ biến mỗi đối phân thớ acyclic giữa hai vật đối phân thớ thành một tương đương yếu thì $F$ cũng biến mỗi tương đương yếu giữa hai vật đối phân thớ thành một tương đương yếu.


• Nếu $F$ biến mỗi phân thớ acyclic giữa hai vật phân thớ thành một tương đương yếu thì $F$ cũng biến mỗi tương đương yếu giữa hai vật phân thớ thành một tương đương yếu.

Chứng minh bổ đề Brown. Hiển nhiên ta chỉ cần chứng minh ý đầu tiên. Giả sử $f: A \tilde{\rightarrow} B$ là một tương đương yếu giữa hai vật đối phân thớ. Các phép bao hàm $i_A: A \to A \sqcup B$ và $i_B: B \to A \sqcup B$ là các đối phân thớ (vì chúng là đẩy ra của các đối phân thớ $\varnothing \to A$ và $\varnothing \to B$. Áp dụng (MC5), ta phân tích $(f,1_B): A \sqcup B \to B$ thành hợp của một phân thớ acyclic $p: X \tilde{\twoheadrightarrow} B$ và một đối phân thớ $j: A \sqcup B \hookrightarrow X$, nghĩa là $pji_A = f$ và $pji_B = 1_B$. Theo (MC2) và Hệ quả 2.3 thì $ji_B: B \to X$ là một tương đương yếu. Mà $j$ và $i_B$ là các phân thớ nên $ji_B$ là một phân thớ (acyclic). Mà $B$ và $X$ các vật đối phân thớ (chú ý rằng $A \sqcup B$ là một vật đối phân thớ) nên theo giả thiết thì $Fj \circ Fi_B$ là một tương đương yếu.Vì $Fp \circ Fj \circ Fi_B = 1_{FB}$ là một tương đương yếu nên $Fp$ là một tương đương yếu theo (MC2) và Hệ quả 2.3. 

Tương tự, $ji_A: A \to X$ là một phân thớ, và là một tương đương yếu do $pji_A = f$ và (MC2), vậy $ji_A$ là một phân thớ acyclic. Mà $A$ và $X$ là các vật đối phân thớ nên theo giả thiết thì $Fj \circ Fi_A$ là một tương đương yếu, suy ra $Ff = Fp \circ Fj \circ Fi_A$ là một tương đương yếu. $\square$

Trở lại chứng minh của Mệnh đề 3.6. Xét phạm trù $\mathbf{Set}$ với cấu trúc mô hình mà các tương đương yếu các các song ánh, và mọi ánh xạ đều là phân thớ cũng như đối phân thớ. Xét hàm tử $F = \text{Hom}_{\mathbf{M}}(A,-) / \simeq_l: \mathbf{M} \to \mathbf{Set}$. Kết quả trường hợp trước nói rằng $Fh = h_\ast$ là một song ánh nếu $h$ là một phân thớ acyclic, vì thế kết luân của bổ đề Brown nói rằng nó cũng là một sonh ánh nếu $h$ là một tương đương yếu giữa hai vật acyclic. $\square$

Mệnh đề 3.7. Nếu $X$ là một vật phân thớ, $f \simeq_l g: A \to X$ và $h: B \to A$ là một cấu xạ thì $fh \simeq_l gh: B \to X$.

Chứng minh. Xét một hình trụ $A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$ và một phép đồng luân $H: C \to X$ giữa $f$ và $g$. Ta phân tích $C \tilde{\rightarrow} A$ thành $C \tilde{\hookrightarrow} C' \tilde{\twoheadrightarrow} A$ (Mệnh đề 2.2), thế thì $A \sqcup A \hookrightarrow C' \tilde{\twoheadrightarrow} A$ lại là một hình trụ. Hơn nữa, vì $X$ là một vật phân thớ, ta có thể áp dụng (MC4) cho biểu đồ giao hoán với các mũi tên liền

để thu được một phép đồng luân $H': C' \to X$ giữa $f$ và $g$. Tóm lại, ta có thể giả sử rằng $C \to A$ là một phân thớ acyclic.

Xét một hình trụ tùy ý $B \sqcup B \hookrightarrow D \tilde{\rightarrow} B$. Xét biểu đồ với các mũi tên liền

Ở đây, hình chữ nhận lớn giao hoán theo định nghĩa của các cấu xạ hiển nhiên $A \sqcup A \to A$ và $B \sqcup B \to B$. Áp dụng (MC4), ta thu được một mũi tên đứt $G$, và ta kiểm tra được (bằng định nghĩa của $\sqcup$) rằng  $HG: D \to X$ là một phép đồng luân giữa $fh$ và $gh$. $\square$

Đảo ngược chiều của các mũi tên trong toàn bộ phần trên, ta thu được khái niệm đồng luân phải.

Định nghĩa. Một vật đường của một vật $X$ là một phân tích $X \tilde{\rightarrow} P \twoheadrightarrow X \times X$ của cấu xạ đường chéo $X \to X \times X$. 

Ta ký hiệu bởi $p_0,p_1: P \to X$ các thành phần của phép phân thớ $(p_0,p_1): P \twoheadrightarrow X \times X$ trong phân tích trên.

Ví dụ 3.8. Trong $\mathbf{Top}$ với mô hình Quillen, nếu $X$ là một CW-phức thì $X^{[0,1]}$ (với tô pô compact-mở) là một vật đường của $X$.

Ví dụ 3.9. Cho $R$ là một vành, trong $\mathbf{Ch}_{\ge 0}(R)$ với mô hình xạ ảnh, xét một phức dây chuyền $A$. Ta có thể lấy phức $P$ với $P_n = A_n \oplus A_n \oplus A_{n+1}$ và vi phân $d(x,y,z) = (dx,dy,dz+y-x)$. 

Định nghĩa. Cho hai cấu xạ $f,g: A \to X$. Một phép đồng luân phải giữa $f$ và $g$ là một vật đường $X \tilde{\rightarrow} P \twoheadrightarrow X \times X$ cùng một cấu xạ $H: A \to P$ sao cho $p_0 H = f$ và $p_1 H = g$. Khi $H$ tồn tại, ta nói $f$ đồng luân phải với $g$ và ký hiệu $f \simeq_r g$.

Mệnh đề 3.10. Nếu $f \simeq_r g: A \to X$ thì với mọi cấu xạ $h: B \to A$, ta có $fh \simeq_l gh: B \to X$.

Bổ đề 3.11. Nếu $X \tilde{\rightarrow} P \twoheadrightarrow X \times X$ là một hình trụ và $X$ là một vật phân thớ thì $p_0,p_1: P \to X$ là các phân thớ acyclic.

Mệnh đề 3.12. Nếu $X$ là một vật phân thớ thì $\simeq_r$ là một quan hệ tương đương trên $\text{Hom}_{\mathbf{M}}(A,X)$.

Cho $X$ là một vật phân thớ và $h: B \to A$ là một cấu xạ. Theo các Mệnh đề 3.10 và 3.12 thì $h$ cảm sinh một ánh xạ $$h^\ast: \text{Hom}_{\mathbf{M}}(A,X) / \simeq_r \to \text{Hom}_{\mathbf{M}}(B,X) / \simeq_r, \qquad [f] \mapsto [fh].$$

Mệnh đề 3.13. Nếu $X$ là một vật phân thớ và $h: B \tilde{\twoheadrightarrow} A$ là một đối phân thớ acyclic thì $h^\ast$ là một song ánh. Kết luận này vẫn đúng nếu $h$ là một tương đương yếu và $B, A$ là các vật đối phân thớ.

Mệnh đề 3.14. Nếu $A$ là một vật đối phân thớ, $f \simeq_r g: A \to X$ và $h: X \to Y$ là một cấu xạ thì $hf \simeq_r hg: A \to Y$.

Sau đây, ta sẽ mô tả cụ thể lớp $\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X)$.

Mệnh đề 3.15. Cho $f,g: A \to X$ là hai cấu xạ.

• Nếu $A$ là một vật đối phân thớ và $f \simeq_l g$ thì $f \simeq_r g$.


• Nếu $X$ là một vật phân thớ và $f \simeq_r g$ thì $f \simeq_l g$.

Chứng minh. Ta chứng minh ý thứ nhất, ý thứ hai thu được bằng cách đảo ngược chiều của các mũi tên.

Xét một hình trụ $A \sqcup A \hookrightarrow C \tilde{\rightarrow} A$ và một phép đồng luân trái $H:  C\to X$ giữa $f$ và $g$. Ký hiệu $j: C  \tilde{\rightarrow}  A$. Vì $A$ là một vật đối phân thớ nên các thành phần $i_0,i_1: A \to C$ là các đối phân thớ acyclic (Bổ đề 3.4). Chọn một vật đường $X \tilde{\rightarrow} P \twoheadrightarrow X \times X$. Nhận xét rằng biểu đồ với các mũi tên liền dưới đây giao hoán, vì $fji_0 = Hi_0 = f$.

Áp dụng (MC4), ta thu được mội mũi tên đứt $K: C \to P$.Thế thì $Ki_1: A \to P$ là một phép đồng luân phải giữa $f$ và $g$, vì $p_0Ki_1 = fji_1 = f$ và $p_1 K i_1 = Hi_1 = g$. $\square$.

Cho $A$ là một vật phân thớ và $X$ là một vật phân thớ. Theo Mệnh đề 3.15, ta có một quan hệ đồng luân $\simeq$ $\text{Hom}_{\mathbf{M}}(A,X)$ mà không cần quan tâm đến trái hay phải nữa. Ký hiệu bởi $[A,X]$ thương của $\text{Hom}_{\mathbf{M}}(A,X)$ bởi $\simeq$.

Định nghĩa. Phạm trù $\pi \mathbf{M}_{cf}$ là phạm trù mà các vật là những vật đồng thời là vật phân thớ cũng như vật đối phân thớ trong $\mathbf{M}$, và các cấu xạ $\text{Hom}_{\pi \mathbf{M}_{cf}}(A,X) = [A,X]$.

Định lý 3.16 (Định lý Whitehead cho phạm trù mô hình). Cho $f: A \to X$ là một cấu xạ giữa hai vật phân thớ và đối phân thớ. Thế thì $f$ là một tương đương yếu khi và chỉ khi nó là một tương đương đồng luân (nghĩa là tồn tại cấu xạ $g: X \to A$ sao cho $fg \simeq 1_X$ và $gf \simeq 1_A$).

Chứng minh. ($\implies$) Giả sử $f$ là một tương đương yếu. Theo Mệnh đề 2.2, ta có thể phân tích $f = pi$, với $i: A \tilde{\hookrightarrow} W$ và $W \tilde{\twoheadrightarrow} X$. Dễ thấy $W$ là một vật phân thớ và đối phân thớ.

Áp dụng (MC4) cho biểu đồ giao hoán với các mũi tên liền

ta thu được một cấu xạ $r: W \to A$ sao cho $ri = 1_A$. Theo Mệnh đề 3.13, $i$ cảm sinh một song ánh $i^\ast: [W,W] \to [A,W]$. Mặt khác, $i^\ast[ir] = [iri] = [i] = i^\ast[1_W]$, nên $[ir] = [1_W]$, hay $ir \simeq 1_W$. Tương tự, tồn tại cấu xạ $s: X \to W$ sao cho $ps = 1_X$ và $sp \simeq 1_W$. Đặt $g = rs: X \to A$, thế thì $fg = pirs \simeq ps = 1_X$ và $gf = rspi \simeq ri = 1_A$.

($\impliedby$) Ngược lại, giả sử $f$ là một tương đương đồng luân. Ta phân tích $f = pi$, với $i: A \tilde{\hookrightarrow} W$ và $p: W \twoheadrightarrow X$ (theo (MC5)). Ta cần chứng minh rằng $p$ là một tương đương yếu. Chú ý rằng $W$ là một vật phân thớ và đối phân thớ. Xét $g: X \to A$ là một cấu xạ sao cho $fg \simeq 1_X$ và $gf \simeq 1_A$. Xét $H: C \to X$ là một phép đồng luân trái giữa $fg$ và $1_X$. vì $pig = fg = Hi_0$ nên biểu đồ với các mũi tên liền dưới đây giao hoán

Ở đây, $i_0$ là một đối phân thớ acyclic theo Bổ đề 3.4. Áp dụng (MC4), ta thu được một mũi tên nét đứt $H': C \to W$. Thế thì $s = H'i_1 \simeq H'i_0 = ig$. Theo chiều thuận của định lý, $i$ là một tương đương đồng luân, nghĩa là tồn tại cấu xạ $r: W \to A$ sao cho $ri \simeq 1_A$ và $ir \simeq 1_W$. Ta có $$sp \simeq spir \simeq sfr \simeq igfr \simeq ir \simeq 1_W,$$ nên tồn tại một phép đồng luân phải $\tilde{H}: W \to \tilde{P}$ giữa $sp$ và $1_W$. Vì $W$ là một vật phân thớ nên các thành phần $q_0,q_1: \tilde{P} \to W$ của vật đường $\tilde{P}$ là các tương đương yếu (Bổ đề 3.11). Do $1_W = q_1 \tilde{H}$ và $1_W$ là một tương đương yếu (Hệ quả 2.3), nên $\tilde{H}$ là một tương đương yếu theo (MC2), suy ra $sp = q_0 \tilde{H}$ cũng là một tương đương yếu. Cuối cùng, ta có biểu đồ giao hoán

(chú ý rằng $ps = pH'i_1 = Hi_1 = 1_X$), nên $p$ là một rút gọn của $sp$, suy ra $p$ cũng là một tương đương yếu theo (MC3). $\square$

Nhắc lại rằng tiên đề (MC5) cho ta các hàm tử $Q, R: \mathbf{M} \to \mathbf{M}$ sao cho $\varnothing \hookrightarrow QX \tilde{\twoheadrightarrow} X$ và $X \tilde{\hookrightarrow} RX \twoheadrightarrow \ast$ (các phép giải (đối) phân thớ). Chúng cho phép mô tả tường minh các cấu xạ giữa hai vật trong phạm trù đồng luân.

Định lý 3.17 (Mô tả phạm trù đồng luân). Phạm trù đồng luân $\mathbf{Ho}(\mathbf{M})$ tương đương với phạm trù $\pi \mathbf{M}_{cf}$. Với mọi vật $A$ và $X$ trong $\mathbf{M}$, ta có $$\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X) \cong [QA,RX].$$ Hơn nữa, nếu một cấu xạ $f: A \to X$ trở thành một đẳng cấu $[f]$ trong $\mathbf{Ho}(\mathbf{M})$ thì $f$ là một tương đương yếu.

Chứng minh. Ta đã biểt $\mathbf{Ho}(\mathbf{M}) \simeq \mathbf{Ho}(\mathbf{M}_{cf})$ theo Bổ đề 2.9. Để chứng minh rằng $\pi: \mathbf{M}_{cf}$ tương đương với $\mathbf{Ho}(\mathbf{M}_{cf})$, ta chứng minh rằng hàm tử thương $\pi: \mathbf{M}_{cf} \to \pi\mathbf{M}_{cf}$ thỏa mãn tính chất phổ dụng của địa phương hóa đối với lớp các tương đương yếu. Thật vậy, cho $\mathbf{C}$ là một phạm trù và $F: \mathbf{M}_{cf} \to \mathbf{C}$ là một hàm tử sao cho $Ff$ là một đẳng cấu với mọi tương đương yếu $f$ (giữa hai vật phân thớ và đối phân thớ). Ta chỉ ra rằng tồn tại duy nhất hàm tử $\bar{F}: \pi \mathbf{M}_{cf} \to \mathbf{C}$ sao cho $\bar{F} \pi = F$. Với $X$ là một vật của $\mathbf{M}_{cf}$, đương nhiên ta phải đặt $\bar{F} X = F X$. Nếu $f$ là một cấu xạ trong $\mathbf{M}_{cf}$, ta cần có $\bar{F} [f] = F f$, vì thế tính duy nhất của $F$ là hiển nhiên. Để chỉ ra sự tồn tại, ta cần chứng minh rằng nếu $f,g: A \to X$ là hai cấu xạ đồng luân giữa hai vật phân thớ và đối phân thớ thì $Ff = Fg$.

Thật vậy, xét một hình trụ $A \sqcup A \hookrightarrow C \tilde{\twoheadrightarrow} A$ và một phép đồng luân trái $H: C \to X$ giữa $f$ và $g$ (ta có thể giả sử $j: C \to A$ là một phân thớ acyclic vì $X$ là một vật phân thớ, như đã làm trong Mệnh đề 3.7). Nói riêng, $C$ là một vật của phạm trù $\mathbf{M}_{cf}$ ($A$ là một vật phân thớ và $A \sqcup A$ là một vật đối phân thớ). Vì $j$ là một tương đương yếu nên $Fj$ là một đẳng cấu, mà $ji_0 = ji_1 = 1_A$ nên $Fj \circ Fi_0 = 1_{FA} = Fj \circ Fi_1$, suy ra $Fi_0 = Fi_1$, do đó $Ff = FH \circ Fi_0 = FH \circ Fi_1 = Fg$.

Vậy $\pi: \mathbf{M}_{cf} \to \pi\mathbf{M}_{cf}$ chính là địa phương hóa của phạm trù $\mathbf{M}_{cf}$ theo lớp các tương tương yếu, hay $\mathbf{Ho}(\mathbf{M})$ tương đương với $\pi \mathbf{M}_{cf}$.

Tiếp theo, ta chỉ ra rằng $\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X) \cong [QA,RX].$ Trước hết, vì $QRA \cong A$ và $QRX \cong X$ trong phạm trù đồng luân nên $$\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X) \cong \text{Hom}_{\mathbf{Ho}(\mathbf{M})}(QRA,QRX) \cong \text{Hom}_{\mathbf{Ho}(\mathbf{M}_{cf})}(QRA,QRX) \cong \text{Hom}_{\pi\mathbf{M}_{cf}}(QRA,QRX) = [QRA, QRX].$$

Mặt khác, $QRA$ là một vật đối phân thớ và $QRX \tilde{\twoheadrightarrow} RX$ là một phân thớ acyclic nên $[QRA,QRX] \cong [QRA, RX]$ theo Mệnh đề 3.6. Tương tự, $RX$ là một vật phân thớ và $QA \tilde{\rightarrow} QRA$ là một tương đương yếu giữa hai vật đối phân thớ (nó là một tương đương yếu vì biểu đồ 

giao hoán, và vì (MC2)), nên $[QRA, RX] \cong [QA, RX]$ theo Mệnh đề 3.13. Vậy ta có $\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X) \cong [QA,RX]$.

Cuối cùng, giả sử $f: A \to X$ là một cấu xạ sao cho $[f]$ là một đẳng cấu trong $\mathbf{Ho}(\mathbf{M})$. Ta đã thấy ở trên rằng $\text{Hom}_{\mathbf{Ho}(\mathbf{M})}(A,X) \cong [QRA, QRX]$, nên $QRf$ là một đẳng cấu trong phạm trù $\pi \mathbf{M}_{cf}$, nghĩa là một tương đương đồng luân. Theo Định lý Whitehead (Định lý 3.16), $QRf$ là một tương đương yếu. Từ biểu đồ giao hoán

và (MC2), ta suy ra rằng $f$ là một tương đương yếu. $\square$

2. Định nghĩa phạm trù mô hình

Định nghĩa (Quillen, 1967). Một phạm trù mô hình là một phạm trù $\mathbf{M}$ cùng ba lớp cấu xạ $\mathscr{W}$, $\mathscr{C}$, $\mathscr{F}$, lần lượt được gọi là các tương đương yếu, đối phân thớ, và phân thớ, lần lượt được ký hiệu bởi $\tilde{\rightarrow}, \hookrightarrow, \twoheadrightarrow$ sao cho các tiên đề sau được thỏa mãn.

• (MC1) Tính đầy đủ. $\mathbf{M}$ có đủ giới hạn nhỏ và đối giới hạn nhỏ.
• (MC2) Hai trong ba. Giả sử $f$ và $g$ là hai cấu xạ sao cho $gf$ được định nghĩa. Nếu hai trong ba cấu xạ $f$, $g$, và $gf$ thuộc $\mathscr{W}$ thì cấu xạ còn lại cũng vậy.
• (MC3) Rút gọn. Nếu một cấu xạ $f$ là một rút gọn của một cấu xạ $g$, và $g \in \mathscr{W}$ (tương ứng, $g \in \mathscr{C}$, $g \in \mathscr{F}$) thì $f$ cũng vậy.
  Ở đây, ta xét phạm trù $\mathbf{M}^{(2)}$ với các vật là các cấu xạ trong $\mathbf{M}$, và các cấu xạ là các hình vuông giao hoán. Ta hiểu $f$ là một rút gọn của $g$ nghĩa là $f$ là một rút gọn của $g$ trong phạm trù $\mathbf{M}^{(2)}$, cụ thể là tồn tại biểu đồ giao hoán
  
  (trong đó hợp của hai cấu xạ ở hai hàng lần lượt là $1_A$ và $1_B$).
• (MC4) Tính chất nâng. Giả sử ta có biểu đồ giao hoán với các mũi tên liền, trong đó $i \in \mathscr{C}$ và $p \in \mathscr{F}$:
  
  nếu $i \in \mathscr{W}$ hoặc $p \in \mathscr{W}$ thì tồn tại mũi tên đứt tạo thành hai tam giác giao hoán. 
• (MC5) Thay thế. Mọi cấu xạ $f: X \to Y$ thừa nhận hai phân tích $$X \tilde{\hookrightarrow} P_f \twoheadrightarrow Y \qquad X \hookrightarrow C_f \tilde{\twoheadrightarrow} Y$$ và các phân tích này có tính hàm tử (nói cách khác, ta có 4 hàm tử $\mathbf{M}^{(2)} \to \mathbf{M}^{(2)}$).

Trong tiên đề (MC4), mũi tên đứt nói chung không duy nhất. Ta nói $i$ có tính chất nâng trái (LLP) đối với $p$ và $p$ có tính chất nâng phải đối với $i$ (RLP), ký hiệu bởi $i \perp p$. Các cấu xạ trong $\mathscr{C} \cap \mathscr{W}$ được gọi là các đối phân thớ acyclic, các cấu xạ trong $\mathscr{F} \cap \mathscr{W}$ được gọi là các phân thớ acyclic.

Theo tiên đề (MC1), $\mathbf{M}$ có vật đầu $\varnothing$ (đối giới hạn của biểu đồ rỗng) cũng như vật cuối $\ast$ (giới hạn của biểu đồ rỗng).

Định nghĩa. Một vật $X$ được gọi là vật đối phân thớ (cofibrant) nếu cấu xạ duy nhất $\varnothing \to X$ là một đối phân thớ, vật phân thớ (fibrant) nếu cấu xạ duy nhất $X \to \ast$ là một phân thớ.

Theo tiên đề (MC5), ta có các hàm tử $Q, R: \mathbf{M} \to \mathbf{M}$, sao cho mọi vật $X$ đều có các phân tích $$\varnothing \hookrightarrow QX \tilde{\twoheadrightarrow} X \qquad X \tilde{\hookrightarrow} RX \twoheadrightarrow \ast$$ đó là các "phép giải (đối) phân thớ".

Ví dụ 2.1. Cho $\mathbf{M}$ là một phạm trù tùy ý. Ta có các cấu trúc mô hình:

• Tương đương yếu: đẳng cấu, đối phân thớ: mọi cấu xạ, phân thớ: mọi cấu xạ.
• Tương đương yếu: đẳng cấu, đối phân thớ: đẳng cấu, phân thớ: mọi cấu xạ.
• Tương đương yếu: đẳng cấu, đối phân thớ: mọi cấu xạ, phân thớ: đẳng cấu.
• Nếu có một cấu trúc mô hình trên $\mathbf{M}$, ta thu được một cấu trúc mô hình trên phạm trù đối $\mathbf{M}^{\text{op}}$ bằng cách đổi vai trò của phân thớ và đối phân thớ.
• Tích của hai phạm trù mô hình là một phạm trù mô hình (với cấu trúc hiển nhiên).

Sau đây là một số tính chất đơn giản.

Mệnh đề 2.2. Cho $(\mathbf{M}, \mathscr{W}, \mathscr{C}, \mathscr{F})$ là một phạm trù mô hình. Ta có các khẳng định sau.

• $i \in \mathscr{C} \iff \forall p \in \mathscr{F} \cap \mathscr{W}, i \perp p$.
• $i \in \mathscr{C} \cap \mathscr{W} \iff \forall p \in \mathscr{F}, i \perp p$.
• $p \in \mathscr{F} \iff \forall i \in \mathscr{C} \cap \mathscr{W}, i \perp p$.
• $p \in \mathscr{F} \cap \mathscr{W} \iff \forall i \in \mathscr{C}, i \perp p$.
• $f \in \mathscr{W} \iff \exists p \in \mathscr{F} \cap \mathscr{W}, \exists p \in \mathscr{C} \cap \mathscr{W}, f = p \circ i$.

Chứng minh. Chiều $\implies$ trong 4 điều kiện đầu tiên là hiển nhiên theo (MC4). Xét chiều $\impliedby$. Giả sử $i$ thỏa mãn tính chất nâng trái với mọi phân thớ acyclic. Theo (MC5), ta có thể phân tích $i$ thành $A \hookrightarrow X \tilde{\twoheadrightarrow} B$. Áp dụng tính chất nâng trái của $i$ vào biểu đồ giao hoán

ta thu được một lớp cắt $h$ của $X \tilde{\twoheadrightarrow} B$. Từ biểu đồ giao hoán

Ta thấy $i$ là một rút gọn của phân thớ $A \hookrightarrow X$, vì thế cũng là một phân thớ. Tương tự, nếu $i$ thỏa mãn tính chất nâng trái với mọi phân thớ, ta xét phân tích $A \tilde{\hookrightarrow} X \twoheadrightarrow B$ và thấy rằng $i$ là một rút gọn của một phân thớ acyclic, vì thế cũng là một phân thớ acyclic. Các tính chất thứ 3 và thứ 4 được chứng minh bằng cách đảo ngược chiều của các mũi tên. Tính chất thứ 5 được suy ra dễ dàng từ (MC2) và (MC5). $\square$

Hệ quả 2.3. Cho $(\mathbf{M}, \mathscr{W}, \mathscr{C}, \mathscr{F})$ là một phạm trù mô hình. 

• Hai trong ba lớp cấu xạ $\mathscr{W}, \mathscr{C}, \mathscr{F}$ xác định lớp còn lại.
• Các lớp $\mathscr{W}, \mathscr{C}, \mathscr{F}$ đóng với phép hợp thành cấu xạ.
• Các lớp $\mathscr{C}$ và $\mathscr{C} \cap \mathscr{W}$ đóng với phép đẩy ra, các lớp $\mathscr{F}$ và $\mathscr{F} \cap \mathscr{W}$ đóng với phép kéo lùi.
• Các đẳng cấu thuộc cả ba lớp $\mathscr{W}, \mathscr{C}, \mathscr{F}$.

Ví dụ 2.4 (Quillen, 1967). Phạm trù $\mathbf{Top}$ có một cấu trúc mô hình với

• tương đương yếu: tương đương đồng luân yếu;
• đối phân thớ: rút gọn của các ánh xạ $i: A \to B$ với $B = \text{colim} B_n$, $B_0 = A$ và $B_{n+1}$ thu được từ $B_n$ bằng cách dán các ngăn (phép bao hàm của CW-phức suy rộng);
• phân thớ: ánh xạ liên tục có tính chất nâng phải với các phép bao hàm $[0,1]^{n-1} \times \{0\} \to [0,1]^n$, $n \ge 1$ (phân thớ Serre);
• vật đối phân thớ: mọi không gian;
• vật phân thớ: rút gọn của các CW-phức suy rộng;

Ví dụ 2.5 (Strøm, 1972). Một cấu trúc khác được cho bởi

• tương đương yếu: tương đương đồng luân;
• đối phân thớ: rút gọn của đối phân thớ Hurewicz với ảnh đóng;
• phân thớ: phân thớ Hurewicz;
• vật đối phân thớ: mọi vật;
• vật phân thớ: mọi vật.

Ví dụ 2.6 (Cole, 2006). Một cấu trúc khác hỗn hợp được cho bởi

• tương đương yếu: tương đương đồng luân yếu (mô hình Quillen);
• đối phân thớ: rút gọn của đối phân thớ theo Strøm, đồng thời thừa nhận phân tích $f \circ i$, với $i$ là một đối phân thớ theo Quillen và $f$ là một tương đương đồng luân;
• phân thớ: phân thớ Hurewicz (mô hình Strøm);

Ví dụ 2.7. Phạm trù $\mathbf{Ch}(R)$ các phức dây chuyền các môđun trên một vành $R$ thừa nhận các cấu trúc mô hình sau đây:

• Mô hình xạ ảnh: Tương đương yếu: tựa đẳng cấu; đối phân thớ: đơn cấu với đối hạch xạ ảnh; phân thớ: toàn cấu (nếu hạn chế lên $\mathbf{Ch}_{\ge 0}(R)$, ta cần xét các ánh xạ dây chuyền toàn cấu ở bậc $\ge 1$).
• Mô hình nội xạ: Tương đương yếu: tựa đẳng cấu; đối phân thớ: đơn cấu; phân thớ: toàn cấu với hạch nội xạ.
• Mô hình Strøm: Tương đương yếu: tương đương đồng luân; đối phân thớ: các ánh xạ dây chuyền có tính chất nâng trái đối với $\text{ev}_0: B^I \to B$; phân thớ: các ánh xạ dây chuyền có tính chất nâng phải đối với $i_0: A \to A \otimes I$; ở đây $I = N_\ast(\Delta^1)$ là hàm tử phức chuẩn hóa đã nhắc đến ở bài https://diendantoanh...g-luân-đơn-hình.

Trước khi tiếp tục, ta nhắc lại về địa phương hóa phạm trù. Cho $\mathbf{M}$ là một phạm trù và $\mathscr{W}$ là một lớp các cấu xạ trong $\mathbf{M}$. Ta muốn một phạm trù mới trong đó mọi cấu xạ trong $\mathscr{W}$ đều trở thành đẳng cấu.

Định nghĩa (Gabriel–Zisman). Một địa phương hóa của $\mathbf{M}$ theo $\mathscr{W}$ là một phạm trù $\mathbf{M}[\mathscr{W}^{-1}]$ cùng một hàm tử $\lambda: \mathbf{M} \to \mathbf{M}[\mathscr{W}^{-1}]$ thỏa mãn tính chất phổ dụng sau. Với mọi hàm tử $F: M \to \mathbf{C}$ sao cho $Ff$ là một đẳng cấu với mọi $f \in \mathscr{W}$, tồn tại duy nhất (sai khác đẳng cấu tự nhiên) hàm tử $G: \mathbf{M}[\mathscr{W}^{-1}] \to \mathbf{C}$ và đẳng cấu tự nhiên $G \lambda \cong F$.

Nói riêng, với mọi $f \in \mathscr{W}$, $\lambda f$ là một đẳng cấu trong $\mathbf{M}[\mathscr{W}^{-1}]$. Điều ngược lại nói chung không đúng, nhưng ta sẽ thấy rằng nó đúng trong phạm trù mô hình.

Mệnh đề 2.8. Địa phương hóa $\mathbf{M}[\mathscr{W}^{-1}]$ tồn tại và là duy nhất sai khác tương đương phạm trù.

Một cách xây dựng ad hoc của $\mathbf{M}[\mathscr{W}^{-1}]$ như sau. Các vật của $\mathbf{M}[\mathscr{W}^{-1}]$ là các vật của $\mathbf{M}$. Một cấu xạ giữa $X$ và $Y$ trong $\mathbf{M}[\mathscr{W}^{-1}]$ là tập thương của:

• tập các đường đi giữa $X$ và $Y$, tạo bởi các cấu xạ trong $\mathbf{M}$, và các cấu xạ trong $\mathscr{W}$ theo chiều ngược (nghịch đảo hình thức của $\mathscr{W}$);
• quan hệ tương đương sinh bởi $X \xrightarrow{f} Y \xleftarrow{f} X \sim X$ với $f \in \mathscr{W}$, và $X \xrightarrow{f} Y \xrightarrow{g} Z \sim X \xrightarrow{gf} Z$.

Phép hợp thành cấu xạ trong $\mathbf{M}[\mathscr{W}^{-1}]$ được cảm sinh từ phép nối đường.

Một cách xây dựng khác: Xét $\mathbf{Arr}$ là phạm trù với hai vật $x, y$ và một cấu xạ không tầm thường duy nhất $x \to y$, và $\mathbf{Iso}$ là phạm trù với hai vật $x,y$ và hai cấu xạ không thường $x \to y$, $y \to x$ là nghịch đảo của nhau. Cho một hàm tử $\mathbf{Arr} \to \mathbf{M}$ (tương ứng, $\mathbf{Iso} \to \mathbf{M}$) cũng là cho một cấu xạ (tương ứng, một đẳng cấu) trong $\mathbf{M}$. Thế thì $\mathbf{M}[\mathscr{W}^{-1}]$ tương đương với đẩy ra của cặp hàm tử $$\bigsqcup_{f \in \mathscr{W}} \mathbf{Arr} \to \mathbf{M} \qquad \bigsqcup_{f \in \mathscr{W}} \mathbf{Arr} \to \bigsqcup_{f \in \mathscr{W}} \mathbf{Iso}.$$

Định nghĩa. Cho $(\mathbf{M}, \mathscr{W}, \mathscr{C}, \mathscr{F})$ là một phạm trù mô hình. Ta định nghĩa phạm trù đồng luân của $\mathbf{M}$ là địa phương hóa $\mathbf{Ho}(\mathbf{M}) = \mathbf{M}[\mathscr{W}^{-1}]$.

Một định lý của Freyd (1970) nói rằng phạm trù $\mathbf{Ho}(\mathbf{Top})$ (tương đương yếu = tương đương đồng luân yếu) không phải là một phạm trù cụ thể, tức là không tồn tại hàm tử trung thành $\mathbf{Ho}(\mathbf{Top}) \to \mathbf{Set}$. Nhìn chung, mô tả tường minh phạm trù đồng luân là một vấn đề phức tạp, chẳng hạn việc xác định xem liệu hai cấu xạ trong phạm trù đồng luân có bằng nhau là một vấn đề không tầm thường.

Phạm trù đồng luân hoàn toàn chỉ phụ thuộc vào lớp $\mathscr{W}$. Điều này cho thấy ý tưởng rằng các lớp $\mathscr{C}$ và $\mathscr{F}$ chỉ đóng vai trò bổ sung thông tin. Bổ đề 2.9 dưới đây cho thấy rằng, để làm việc với phạm trù đồng luân, ta chỉ cần quan tâm đến các vật (đối) phân thớ.

Định nghĩa. Ký hiệu bởi $\mathbf{M}_c$ (tương ứng, $\mathbf{M}_f$, tương ứng, $\mathbf{M}_{cf}$ phạm trù con đầy của $\mathbf{M}$ sinh bởi các vật đối phân thớ (tương ứng, vật phân thớ, tương ứng, vật phân thớ và đối phân thớ). Ta cũng định nghĩa phạm trù đồng luân của chúng bởi địa phương hóa theo lớp $\mathscr{W}$.

Bổ đề 2.9. Các phép bao hàm cảm sinh các tương đương phạm trù

Chứng minh. Xét phép bao hàm $\mathbf{M}_f \subset \mathbf{M}$. Nó biến tương đương yếu thành tương đương yếu, nên cảm sinh một hàm tử $\mathbf{Ho}(\mathbf{M}_f) \to \mathbf{Ho}(\mathbf{M})$. Ngược lại, ta có hàm tử "giải phân thớ" $R: \mathbf{M} \to \mathbf{M}_f$, nó cảm sinh một hàm tử $\mathbf{Ho}(\mathbf{M}) \to \mathbf{Ho}(\mathbf{M}_f)$. Ta kiểm tra được rằng chúng là nghịch đảo (sai khác đẳng cấu tự nhiên) của nhau. $\square$

Khái niệm phạm trù mô hình (model category) được đưa ra bởi Quillen năm 1967, trong nỗ lực tổng quát hóa đại số đồng điều thành lý thuyết đồng luân cho các đối tượng không abel như không gian tô pô, nhóm, đại số trên một vành... Ngôn ngữ phạm trù mô hình và khái niệm đồng luân tổng quát là một phần quan trọng trong K-lý thuyết đại số cũng như hình học đại số.

Một phần của lý thuyết phạm trù mô hình và đồng luân là lý thuyết đồng luân đơn hình đã được viết ở bài https://diendantoanh...g-luân-đơn-hình.

Chúng ta sẽ trình bày những khái niệm và kết quả cơ bản của lý thuyết này.

1. Ví dụ: Không gian tô pô và phức dây chuyền

Xét phạm trù $\mathbf{Top}$ các không gian tô pô.

Nhắc lại rằng hai ánh xạ liên tục $f, g: X \to Y$ được gọi là đồng luân nếu tồn tại ánh xạ liên tục $H: X \times [0,1] \to Y$ sao cho $H(-,0) = f$ và $H(-,1) = g$ (một phép đồng luân giữa $f$ và $g$). Khi đó, ta ký hiệu $f \simeq g$.

Hai không gian $X$ và $Y$ được gọi là tương đương đồng luân nếu tồn tại các ánh xạ liên tục $f: X \leftrightarrows Y: g$ sao cho $fg \simeq 1_Y$ và $gf \simeq 1_X$. Khi đó, ta ký hiệu $X \simeq Y$.

Nếu $(X,x)$ và $(Y,y)$ là các không gian định điểm, ta ký hiệu hởi $[(X,x), (Y,y)]$ thương của tập hợp các ánh xạ định điểm $(X,x) \to (Y,y)$ bởi quan hệ đồng luân định điểm (một phép đồng luân định điểm $H$ giữa hai ánh xạ định điểm là một phép đồng luân sao cho $H(-,t)$ là ánh xạ định điểm với mọi $t \in [0,1]$). Với $n \ge 0$, Ký hiệu bởi $\pi_n(X,x) = [(\mathbb{S}^n,\ast),(X,x)]$. Ta có các hàm tử $\pi_n: \mathbf{Top}_\ast \to \mathbf{Set}$, hơn nữa $\pi_1$ là nhóm và $\pi_n$ là nhóm abel với $n \ge 2$. 

Mệnh đề 1.1. Nếu $f: X \to Y$ là một tương đương đồng luân thì $\pi_0(f): \pi_0(X,x) \to \pi_0(Y,f(x))$ là một song ánh, và với mọi $x \in X$ cũng như $n \ge 1$ thì $\pi_n(f): \pi_n(X,x) \to \pi_n(Y,f(x))$ là một đẳng cấu nhóm.

Định nghĩa. Một tương đương đồng luân yếu là một ánh xạ liên tục $f: X \to Y$ sao cho các ánh xạ cảm sinh $\pi_n(f)$ thỏa mãn các điều kiện ở mệnh đề trên. Ta ký hiệu tương đương đồng luân yếu bởi $\tilde{\rightarrow}$. Hai không gian $X$ và $Y$ được gọi là tương đương yếu nếu tồn tại các tương đương đồng luân yếu $$X \tilde{\leftarrow} X_1 \tilde{\rightarrow} \cdots \tilde{\leftarrow} X_n \tilde{\rightarrow} Y.$$

Hiển nhiên, hai không gian tương đương yếu thì các nhóm đồng luân tương ứng đẳng cấu.

Trong các không gian tô pô, các CW-phức (hoặc các phức đơn hình...) đóng vai trò như những mô hình tổ hợp để tính toán các nhóm đồng luân. Thực tế, ta chỉ cần quan tâm đến lý thuyết đồng luân của chúng, nhờ vào các định lý sau đây.

Định lý 1.2. Với mỗi không gian tô pô $X$, tồn tại một CW-phức $Z$ và một tương đương đồng luân yếu $Z \to \tilde{\rightarrow} X$.

Định lý 1.3 (Xấp xỉ CW). Mỗi ánh xạ liên tục giữa hai CW-phức đều đồng luân với một ánh xạ phân phân ngăn.

Hơn nữa, để nói về tương đương đồng luân giữa các CW-phức, ta chỉ cần quan tâm đến tương đương yếu, nhờ

Định lý 1.4 (Whitehead). Mỗi tương đương đồng luân yếu giữa hai CW-phức là một tương đương đồng luân.

Mục đích của khái niệm phạm trù mô hình là cho phép, trong một phạm trù bất kỳ, nói về:

• thế nào là "giống nhau sai khác đồng luân" (tương đương đồng luân) giữa hai vật;
• thế nào là một phép đồng luân, một tương đương đồng luân;
• những vật nào là đủ "tốt" (những "mô hình") mà trên đó ta chỉ cần quan tâm đến các tương đương đồng luân yếu.

Một phạm trù khác nơi ta có thể làm lý thuyết đồng luân là phạm trù các phức dây chuyền (đồng luân ở đây được biến đến dưới dạng đại số đồng điều). Cho $R$ là một vành. Xét phạm trù $\mathbf{Ch}_{\ge 0}(R)$ các phức dây chuyền (chiều của vi phân là chiều giảm) các $R$-môđun tập trung ở bậc không âm.

Một phép đồng luân dây chuyền giữa hai ánh xạ dây chuyền $f, g: A \to B$ là một dãy các đồng cấu $h: A_n \to B_{n+1}$ sao cho $f - g = hd + dh$. Khi $h$ tồn tại, ta nói $f$ và $g$ đồng luân và ký hiệu $f \simeq g$.

Hai phức dây chuyền $A$ và $B$ được gọi là tương đương đồng luân nếu tồn tại các ánh xạ dây chuyền $f: A \leftrightarrows B: g$ sao cho $fg \simeq 1_B$ và $gf \simeq 1_A$. Khi đó, ta ký hiệu $A \simeq B$.

Mệnh đề 1.5. Nếu $f: A \to B$ là một tương đương đồng luân thì nó cảm sinh đẳng cấu $H_n(f): H_n(A) \to H_n(B)$ với mỗi $n \ge 0$.

Định nghĩa. Một tựa đẳng cấu là một ánh xạ dây chuyền $f: A \to B$ sao cho $H_n(f)$ là một đẳng cấu với mỗi $n \ge 0$. Ta ký hiệu tựa đẳng cấu bởi $\tilde{\rightarrow}$. Hai phức dây chuyền $A$ và $B$ được gọi là tựa đẳng cấu nếu tồn tại các tựa đẳng cấu $$A \tilde{\leftarrow} A_1 \tilde{\rightarrow} \cdots \tilde{\leftarrow} A_n \tilde{\rightarrow} B.$$

Hiển nhiên, hai phức tựa đẳng cấu thì các nhóm đồng điều tương ứng đẳng cấu.

Nhắc lại rằng một $R$-môđun $P$ được gọi là xạ ảnh nếu hàm tử $\text{Hom}_R(P,-): {}_R\mathbf{Mod} \to \mathbf{Ab}$ khớp (bảo toàn toàn cấu). Một $R$-môđun $I$ được gọi là nội xạ nếu hàm tử $\text{Hom}_R(-,I): {}_R\mathbf{Mod} \to \mathbf{Ab}$ khớp (biến đơn cấu thành toàn cấu). 

Mệnh đề 1.6. Cho $f: A \to B$ là một tựa đẳng cấu giữa hai phức tập trung ở bậc không âm. Nếu $A$ nội xạ ở mọi bậc hoặc $B$ xạ ảnh ở mọi bậc thì $f$ là một tương đương đồng luân.

Như vậy, nếu muốn làm đại số đồng điều trong đó các phức sai khác tựa đẳng cấu, ta có hai mô hình:

• mô hình "xạ ảnh", nơi các vật "tốt ở nguồn" là các môđun xạ ảnh, và mọi vật đều "tốt ở đích". Mỗi $R$-môđun đều có một giải xạ ảnh $P_{\bullet} \to M$, nó đóng vai trò như các CW-phức cho các không gian tô pô.
• mô hình "nội xạ", nơi mọi vật đều "tốt ở nguồn" và các vật "tốt ở đích" là các môđun nội xạ.  Mỗi $R$-môđun đều có một giải nội xạ $M \to I_{\bullet}$, nó đóng vai trò đối ngẫu so với các CW-phức cho các không gian tô pô.

Một trong những mục tiêu của lý thuyết đồng luân của Quillen là tổng quát hóa khái niệm "giải" ở trên cho các phạm trù không abel.

Ta nhắc lại về dãy khớp dài. Giả sử $0 \to A \xrightarrow{i} B \xrightarrow{p} C \to 0$ là một dãy khớp ngắn các phức dây chuyền, khi đó ta có dãy khớp dài $$\cdots \to H_n(A) \xrightarrow{i_\ast} H_n(B) \xrightarrow{p_\ast} H_n(C) \xrightarrow{\partial} H_{n-1}(A) \to \cdots \to H_0(C) \to 0,$$ trong đó $\partial$ là các đồng cấu nối. Có hai cách xây dựng các đồng cấu nối.

1. Ta có thể xét ánh xạ dây chuyền $i: A \to B$ tùy ý (không nhất thiết là đơn cấu). Nón (cone) của $i$ là phức $C(i)$ cho bởi $B_n \oplus A_{n-1}$ ở bậc $n$ và vi phân $d(b,a) = (d(b) + i(a), d(a))$. Khi đó ta có dãy khớp dài ở trên khi thay $C$ bởi $C(i)$. Đồng cấu nối $\partial$ được cảm sinh từ phép chiếu $C(i) \to A[-1]$. Khi $i$ là đơn cấu, ta kiểm tra được rằng $C(i)$ tựa đẳng cấu với $C$.
2. Ta cũng có thể xét ánh xạ dây chuyền $p: B \to C$ tùy ý (không nhất thiết là toàn cấu). Thớ đồng luân (homotopy fiber) của $p$ là phức $K(p)$ cho bởi $B_n \oplus C_{n+1}$ ở bậc $n$ và vi phân $d(b,c) = d(b), p(b) + d(c))$. Khi đó ta có dãy khớp dài ở trên khi thay $A$ bởi $K(p)$. Đồng cấu nối $\partial$ được cảm sinh từ phép chiếu nhúng $C[1] \to K(p)$. Khi $p$ là toàn cấu, ta kiểm tra được rằng $K(p)$ tựa đẳng cấu với $A$.

Để xây dựng dãy khớp dài cho các nhóm đồng luân của các không gian tô pô, ta cần các khái niệm tương tự (theo nghĩa đồng luân) với khái niệm đơn cấu và toàn cấu của phức dây chuyền. Đó là khái niệm (đối) phân thớ.

Định nghĩa 1.7. Một phân thớ Hurewicz là một ánh xạ liên tục $p: E \to B$ sao cho trong mọi biểu đồ giao hoán

$H$ có thể nâng thành một ánh xạ liên tục $\tilde{H}$. Nói cách khác, nếu ta có một phép đồng luân $H: X \times [0,1] \to B$ giữa hai ánh xạ liên tục $f,g: X \to B$ và một nâng $\tilde{f}: X \to E$ của $f$, thế thì ta có thể nâng $H$ thành một phép đồng luân giữa $\tilde{f}$ và một nâng $\tilde{g} = \tilde{H}(-,1)$ của $g$.

Mệnh đề 1.8. Kéo lùi của một phân thớ Hurewicz là một phân thớ Hurewicz.

Ví dụ 1.9. Cho $f: X \to Y$ là một ánh xạ liên tục. Ta định nghĩa không gian đường của $f$ bởi $$P_f = Y^{[0,1]} \times_Y X = \{(\gamma,x) \,|\, \gamma: [0,1] \times X, x \in X, \gamma(0) = f(x)\},$$ trong đó tô pô trên $Y^{[0,1]}$ là tô pô compact-mở. Thế thì ánh xạ $\text{ev}_1: P_f \to Y$ cho bởi $\text{ev}_1(\gamma,x) =\gamma(1)$ là một phân thớ Hurewicz. Hơn nữa, ta có phân tích $X \tilde{\hookrightarrow} P_f \xrightarrow{\text{ev}_1} Y$ - nghĩa là có thể phân tích mọi ánh xạ liên tục thành hợp của một phân thớ và một tương đương đồng luân yếu.

Mệnh đề 1.10. Cho $p: E \to B$ là một phân thớ với $B$ liên thông đường. Khi đó các thớ $E_b = p^{-1}(b)$ (với $b \in B$) tương đương đồng luân. Nếu ta lấy $b_0 \in B$, $F = p^{-1}(b_0)$ và $f_0 \in F$ thì ta có dãy khớp dài các nhóm đồng luân $$\cdots \to \pi_n(F,f_0) \to \pi_n(E,f_0) \to \pi_n(B,b_0) \to \pi_{n-1}(F,f_0) \to \cdots$$

Một cách đối ngẫu, ta có

Định nghĩa 1.11. Một đối phân thớ (Hurewicz) là một ánh xạ liên tục $i: A \to X$ sao cho trong mọi biểu đồ giao hoán

$h$ có thể mở rộng thành một ánh xạ liên tục $H$. Nói cách khác, nếu ta có một ánh xạ liên tục $f: X \to Y$ và một phép đồng luân giữa $h$ "hạn chế" $f \circ i = f|_A$ và một ánh xạ khác $g: A \to Y$, thì ta có thể mở rộng $h$ lên cả $X$.

Mệnh đề 1.12. Một đối phân thớ $i: A \to X$ cảm sinh một phép đồng phôi $i: A \to i(A)$. Nếu $X$ Hausdorff thì $i(A)$ đóng. 

Ví dụ 1.13. Phép bao hàm của một CW-phức con trong một CW-phức là một đối phân thớ.

Ví dụ 1.14. Cho $f: A \to X$ là một ánh xạ liên tục. Ta định nghĩa hình trụ của $f$ bởi $$C_f = (A \times [0,1] \sqcup X) / \left\langle(a,0) \sim f(a): a \in A \right\rangle.$$ Ta có phân tích của $f$ thành hợp của một tương đương đồng luân yếu và một đối phân thớ $A \hookrightarrow C_f \tilde{\rightarrow} X$.

Cho hai ánh xạ liên tục $f,g: A \to X$. Nhận xét rằng, với $\gamma = (1_A,1_A): A \sqcup A \to A$ là ánh xạ hiển nhiên, cho một phép đồng luân giữa $f$ và $g$ cũng là cho một ánh xạ liên tục $H: C_\gamma \to Y$ sao cho hợp $A \sqcup A \to C_f \to X$ chính là ánh xạ $(f,g)$. Một cách đối ngẫu, xét $\delta = (1_X,1_X): X \to X \times X$ là ánh xạ đường chéo. Thế thì cho một ánh xạ liên tục $H: X \to P_\delta$ sao cho $\text{ev}_0 \circ H = f$ và $\text{ev}_1 \circ H = g$ cũng là cho một ánh xạ liên tục $u: A \to X$ cùng hai phép đồng luân $f \simeq u \simeq g$.

Định nghĩa. Cho $(X,A)$ là một cặp không gian và $a \in A$. Ta định nghĩa các tập hợp đồng luân tương đối $\pi_n(X,A)$ (với $n \ge 1$) là thương của tập hợp các ánh xạ liên tục $\gamma: [0,1]^n \to X$ sao cho $\gamma(\partial [0,1]^n) \subset A$ và $\gamma(\partial [0,1]^n \setminus ([0,1]^{n-1} \times \{0\})) \subset A = \{a\}$ sai khác đồng luân tương đối $A$. Đó là một nhóm với $n \ge 2$ và là một nhóm abel với $n \ge 3$.

Mệnh đề 1.15. Ta có dãy khớp dài các nhóm đồng luân $$\cdots \to \pi_n(A) \to \pi_n(X) \to \pi_n(X,A) \to \pi_{n-1}(A) \to \cdots$$

We say that $f(x)$ has limit $L$ (or $f(x)$ converges to $L$) when $x$ tends to $a$, denoted by $\lim_{x \to a} f(x) = L$, if

• formally, $\forall \varepsilon > 0, \exists \delta > 0, \forall x, \quad 0 < |x - a| < \delta \implies |f(x) - L| < \varepsilon$;
• less formally, for any given tolerance $\varepsilon > 0$, there is a sufficiently small threshold $\delta > 0$ such that whenever $x$ is closer to $a$ than this threshold, then $f(x)$ is closer to $L$ than the given tolerance;
• informally, $f(x)$ can be arbitrarily close to $L$, provided that $x$ is sufficiently close to $a$.

It's like playing a 2-player game: the first player give an $\varepsilon > 0$, and the second has to respond using a $\delta > 0$. 

Proving $\lim_{x \to a} f(x) = L$ is to show that a response $\delta$ exists for every $\varepsilon$.

Example of non-existing limit: The function $f(x) = \dfrac{1}{x}$ has no limit as $x \to 0$.

We may show this by contradiction: Suppose that $\lim_{x \to 0} \dfrac{1}{x} = L$ for some $L \in \mathbb{R}$.

By definition, $$\forall \varepsilon > 0, \exists \delta > 0, \forall x, \quad 0 < |x| < \delta \implies \left|\frac{1}{x} - L\right| < \varepsilon.$$

This is a claim which holds for all $\varepsilon > 0$, in particular it holds for (let us say) $\varepsilon = 1$ (specialization of the quantifier $\forall$). Hence $$\exists \delta > 0, \forall x, \quad 0 < |x| < \delta \implies \left|\frac{1}{x} - L\right| < 1.$$

(In words, there exists a $\delta > 0$ such that $\left|\dfrac{1}{x} - L\right| < 1$ whenever $0 < |x| < \delta$). Let us show that the existence of such a $\delta$ is contradictory. Indeed, if such $\delta$ existed, let us take $x > 0$ which is sufficiently small such that $x < \frac{1}{|L| + 1}$ and $x < \delta$, says $$x = \frac{1}{2}\min\left\{\delta, \frac{1}{|L| + 1}\right\}.$$ On the one hand, since $0 < x < \delta$, the definition of $\delta$ gives $$\left|\dfrac{1}{x} - L\right| < 1.$$

On the other hand, $$\left|\dfrac{1}{x} - L\right|  \ge \frac{1}{|x|} - |L| > |L| + 1 - |L| = 1.$$ This contradiction conludes the proof.

Dùng tiêu chuẩn Cauchy thôi.

Vì $\lim_{n \to \infty}\dfrac{x_{n+1}}{x_n} = \dfrac{1}{2}$ nên tồn tại $N \in \mathbb{N}$ sao cho $\dfrac{x_{n+1}}{x_n} < \dfrac{3}{4}$ với mọi $n \ge N$.

Từ đó với mọi $n > N$ thì $x_n < \left(\dfrac{3}{4}\right)^{n - N} x_N$.

Xét $m > n \ge N$, ta có $$\begin{align*}|s_m - s_n| & = x_{n+1} + \cdots + x_m \\ & < \left(\dfrac{3}{4}\right)^{n+1 - N} x_N + \cdots + \left(\dfrac{3}{4}\right)^{m - N} x_N \\ & =  \left(\dfrac{3}{4}\right)^{n+1 - N}x_N\dfrac{1 -  \left(\dfrac{3}{4}\right)^{n-m}}{1 - \dfrac{3}{4}} \\ & < 4x_N\left(\dfrac{3}{4}\right)^{n+1 - N} \end{align*}.$$ Cố định $\varepsilon > 0$ và lấy $$n_\varepsilon = N + \max\left\{\left\lfloor\frac{\ln 4 + \ln x_N - \ln \varepsilon}{\ln 4 - \ln 3} \right \rfloor,0 \right\}.$$ Thế thì $n_\varepsilon \ge N$ cũng như $n_\varepsilon - N + 1 > \frac{\ln 4 + \ln x_N - \ln \varepsilon}{\ln 4 - \ln 3}$, hay $\left(\dfrac{4}{3}\right)^{n_{\varepsilon} + 1 - N} > \frac{4x_N}{\varepsilon}$, do đó với $m > n \ge n_\varepsilon$ thì $$|s_m - s_n| < 4x_N\left(\dfrac{3}{4}\right)^{n+1 - N} \le 4x_N\left(\dfrac{3}{4}\right)^{n_{\varepsilon}+1 - N} < \varepsilon.$$

Ở cấp phổ thông trở xuống, các bạn học sinh dùng dấu “⇒” rất tuỳ tiện: dấu ⇒ vốn là một toán tử dùng để nối hai mệnh đề, tạo ra một mệnh đề mới, nhưng rất nhiều bạn lại dùng nó như một liên từ (viết tắt thay cho “suy ra”, “vì thế”,…). Điều này gây trở ngại về tư duy khi học lên cao hơn: rất nhiều sinh viên không hiểu được những suy luận cơ bản kiểu “nếu A thì B”… và khi đụng đến những định nghĩa dài kiểu 2-3 lượng từ như định nghĩa hàm liên tục thì đa số sinh viên tê liệt.

> 0, ∀x, |x - a| < δ ⇒ |f(x) - f(a)| < ε

Đề thiếu, cần thêm giả thiết $m,n \ge 2$ (với $m = 2, n = 1$ thì $F_m | F_n$ nhưng $m \not | n$).

Bước 1. Chứng minh rằng $\gcd(F_m, F_{m-1}) = 1$ (quy nạp theo $m$).

Bước 2. Chứng minh rằng $F_{m+k} = F_{k+1}F_m + F_k F_{m-1}$ với mọi $k \ge 1$ (quy nạp theo $k$).

Bước 3. Chứng minh mệnh đề đã cho bằng quy nạp theo $n$.

Xét $n \le m$. Nếu $n < m$ thì $0 < F_n < F_m$ nên $F_m \not | F_n$. Nếu $n = m$ thì hiển nhiên $F_m | F_n$.

Do đó với $n \le m$ thì khẳng định "$F_m | F_n \Leftrightarrow m | n$" đúng.

Xét $n > m$, dùng kết quả Bước 2 cho $k = n - m$, ta được $F_n = F_{n-m+1} F_m + F_{n-m}F_{m-1}$. Do đó $$F_m | F_n \Leftrightarrow F_m | F_{n-m}F_{m-1}  \Leftrightarrow F_m | F_{n-m}$$ (dùng kết quả Bước 1). Giờ áp dụng giả thiết quy nạp cho số $n - m$: $$F_m | F_n \Leftrightarrow F_m | F_{n-m} \Leftrightarrow m | n-m \Leftrightarrow m | n.$$

5 - ĐỊNH LÝ CHEVALLEY-SHEPHARD-TODD

Ở mục này, ta trả lời câu hỏi khi nào $\mathbb{C}[x_1,\ldots,x_n]^G$ có phân tích Hironaka đơn giản nhất: $\mathbb{C}[x_1,\ldots,x_n]^G = \mathbb{C}[\theta_1,\ldots,\theta_n]$, tức là một đại số đa thức.

Chú ý rằng vì $G$ là một nhóm ma trận hữu hạn nên mọi ma trận $g \in G$ đều chéo hóa được.

Định nghĩa. Ta gọi một ma trận $\sigma \in \text{GL}_n(\mathbb{C})$ là một phép giả phản xạ nếu $1$ là một giá trị riêng của $\sigma$ với bội $n-1$.

Nói cách khác, $\sigma$ là một phép giả phản xạ nếu $\sigma \neq \text{id}$ và $\sigma$ cố định một siêu phẳng. Chẳng hạn, khi nhúng $S_n \hookrightarrow \text{GL}_n(\mathbb{C})$ (các ma trận hoán vị) thì các chuyển vị (2-chu trình) là các phép giả phản xạ, vì khối $\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$ có 2 giá trị riêng là $1$ và $-1$. Vậy nhóm $S_n$ được sinh bởi các phép giả phản xạ.

Định lý Chevalley-Shephard-Todd. Đại số con bất biến $\mathbb{C}[x_1,\ldots,x_n]^G$ là một đại số đa thức khi và chỉ khi $G$ được sinh bởi các phép giả phản xạ.

Chú ý rằng việc được sinh bởi các phép giả phản xạ không phải một tính chất nội tại của nhóm hữu hạn $G$, nó phụ thuộc vào phép nhúng $G \hookrightarrow \text{GL}_n(\mathbb{C})$.

Ta bắt đầu chứng minh điều kiện đủ.

Nếu $\sigma \in \text{GL}_n(\mathbb{C})$ là một phép giả phản xạ thì $H_{\sigma} = \sigma - \text{id}$ là siêu phẳng được cố định bởi $\sigma$. Nó được định nghĩa bởi phương trình $L_{\sigma} = 0$, với $L_{\sigma} \in \mathbb{C}[x_1,\ldots,x_n]$ là một đa thức thuần nhất bậc 1. Nhân xét rằng với mọi $f \in \mathbb{C}[x_1,\ldots,x_n]$, đa thức $\sigma \cdot f - f$ chia hết cho $L_{\sigma}$. Thật vậy, theo định nghĩa của $H_{\sigma}$ thì $(\sigma \cdot f - f)(v) = 0$ với mọi $v \in H_{\sigma}$, nên theo Hilberts Nullstellensatz thì một lũy thừa nào đó của $\sigma \cdot f - f$ chia hết cho $L_{\sigma}$. Vì $L_{\sigma}$ bất khả quy nên bản thân $\sigma \cdot f - f$ chia hết cho $L_{\sigma}$.

Mệnh đề 1. Giả sử $G \subseteq \text{GL}_n(\mathbb{C})$ là một nhóm ma trận hữu hạn được sinh bỏi các phép giả phản xạ. Ký hiệu bởi $I$ ideal của $\mathbb{C}[x_1,\ldots,x_n]$ sinh bởi các đa thức bất biến thuần nhất bậc dương. Nếu $h_1,\ldots,h_m \in \mathbb{C}[x_1,\ldots,x_n]$ là các đa thức thuần nhất và $g_1,\ldots,g_m \in \mathbb{C}[x_1,\ldots,x_n]^G$ sao cho $h_1 g_1 + \cdots + h_m g_m = 0$ thì $h_1 \in I$, hoặc $g_1 \in \langle g_2,\ldots,g_m \rangle$.

Chứng minh. Quy nạp theo bậc của $h_1$.

• Nếu $h_1 = 0$ thì hiển nhiên $h_1 \in I$.
• Nếu $h_1$ là một hằng số khác $0$ thì $g_1 = -\frac{h_2}{h_1}g_2 - \cdots - \frac{h_m}{h_1}g_m \in \langle g_2,\ldots,g_m \rangle$.
• Nếu $\deg(h_1) > 0$, ta giả sử $g_1 \notin \langle g_2,\ldots,g_m \rangle$. Xét $\sigma \in G$ là một phép giả phản xạ. Với mỗi $i = 1,\ldots,m$, ta có thể viết $\sigma \cdot h_i  - h_i = L_\sigma \tilde{h}_i$, từ đó $$0 = \sigma \cdot (h_1 g_1 + \cdots + h_m g_m) - (h_1 g_1 + \cdots + h_m g_m) = L_\sigma \tilde{h}_1g_1 + \cdots + L_\sigma \tilde{h}_mg_m,$$ suy ra $\tilde{h}_1g_1 + \cdots + \tilde{h}_mg_m = 0$. Ta có $\deg(\tilde{h}_1) < \deg(h_1)$ và $g_1 \notin \langle g_2,\ldots,g_m \rangle$, nên theo giả thiết quy nạp thì hoặc $\tilde{h}_1 \in I$, suy ra $\sigma \cdot h_1  - h_1 = L_\sigma \tilde{h}_1 \in I$. Hiển nhiên $I$ ổn định dưới tác động của $G$ nên nếu $\sigma_1,\ldots,\sigma_r \in G$ là các phép giả phản xạ thì $$\sigma_1 \cdots \sigma_r \cdot h_1 - h_1 = \sigma_1 \cdots \sigma_{r-1}(\sigma_r \cdot h_1 - h_1) + \cdots + (\sigma_1 \cdot h_1 - h_1) \in I,$$ do đó $\sigma \cdot h_1 - h_1 \in I$ với mọi $\sigma \in G$, vì $G$ được sinh bởi các phép giả phản xạ. Từ đó ta có $$h_1^\ast - h_1 = \frac{1}{|G|} \sum_{\sigma \in G}(\sigma \cdot h_1 - h_1) \in I,$$ suy ra $h_1 \in I$ vì $h_1^\ast$ bất biến và thuần nhất. $\square$

Chứng minh điều kiện đủ trong định lý Chevalley-Shephard-Todd. Giả sử $G \subseteq \text{GL}_n(\mathbb{C})$ được sinh bỏi các phép giả phản xạ. Ta vẫn ký hiệu bởi $I$ ideal của $\mathbb{C}[x_1,\ldots,x_n]$ sinh bởi các đa thức bất biến thuần nhất bậc dương, thế thì tồn tại các đa thức thuần nhất bậc dương $f_1,\ldots,f_m \in \mathbb{C}[x_1,\ldots,x_n]^G$ sao cho $I = \langle f_1,\ldots,f_m\rangle$ theo định lý cơ sở Hilbert. Ta đã biết (theo chứng minh của định lý hữu hạn Hilbert) rằng $\mathbb{C}[x_1,\ldots,x_n]^G = \mathbb{C}[f_1,\ldots,f_m]$.

Chọn hệ sinh $f_1,\ldots,f_m$ (của $I$) sao cho $m$ nhỏ nhất có thể. Ta chứng minh $f_1,\ldots,f_m$ độc lập đại số trên $\mathbb{C}$ (nói riêng, $m = n$ vì chiều Krull của $\mathbb{C}[x_1,\ldots,x_n]^G$ bằng $n$). Giả sử phản chứng rằng tồn tại đa thức $g \in \mathbb{C}[y_1,\ldots,y_m] \setminus \{0\}$ sao cho $g(f_1,\ldots,f_m) = 0$ (nói riêng, $g$ khác hằng). Chọn $g$ có bậc nhỏ nhất như vậy. Hơn nữa, ta có thể giả sử rằng tồn tại số nguyên dương sao cho mọi đơn thức $y_1^{j_1} \cdots y_m^{j_m}$ xuất hiện trong $g$ thỏa mãn $j_1 \deg(f_1) + \cdots + j_m \deg(f_m) = d$ (chọn $d$ sao cho có ít nhất một đơn thức như vậy, rồi thay $g$ bởi tổng của các đơn thức như vậy của nó). Nói cách khác, khi khai triển $g(f_1,\ldots,f_m)$, các đơn thức $x_1^{i_1} \cdots x_n^{i_n}$ nhận được đều có bậc $i_1 + \cdots + i_n = d$.

Đặt $g_i = \dfrac{\partial g}{\partial y_i}(f_1,\ldots,f_m) \in \mathbb{C}[x_1,\ldots,x_m]^G$, $i=1,\ldots,m$. Thế thì $g_i$ thuần nhất bậc $d - \deg f_i$. Vì $g$ khác hằng nên tồn tại chỉ số $i$ sao cho $\dfrac{\partial g}{\partial y_i} \neq 0$. Hơn nữa với các chỉ số $i$ như vậy thì $\dfrac{\partial g}{\partial y_i}$ có bậc nhỏ hơn $g$ nên $g_i \neq 0$ theo cách chọn $g$.

Ký hiệu bởi $J$ ideal của $\mathbb{C}[x_1,\ldots,x_n]$ sinh bởi $g_1,\ldots,g_m$. Đánh số lại sao cho $g_1,\ldots,g_k$ là hệ sinh cự tiểu của $J$ $(k \le m)$. Với $k+1 \le i \le m$, viết $g_i = h_{i1}g_1 + \cdots + h_{ik} g_k$, trong đó $h_{ij} = 0$ hoặc thuần nhất bậc $\deg(g_i) - \deg(g_j) = \deg(f_j) - \deg(f_i)$. Nói riêng, $h_{ij}f_i$ thuần nhất bậc $\deg(f_j)$.

Với $s=1,\ldots,n$, ta có $$\begin{align*} 0 & = \dfrac{\partial}{\partial x_s}(g(f_1,\ldots,f_m)) \\ & = \sum_{i=1}^m g_i \dfrac{\partial f_i}{\partial x_s} \\ & = \sum_{i=1}^k g_i \dfrac{\partial f_i}{\partial x_s} + \sum_{i=k+1}^m \left(h_{i1}g_1 + \cdots + h_{ik} g_k\right) \dfrac{\partial f_i}{\partial x_s} \\ & = \sum_{i=1}^k g_i \left(\dfrac{\partial f_i}{\partial x_s} + \sum_{j=k+1}^m h_{ji} \dfrac{\partial f_j}{\partial x_s}\right). \end{align*}$$ Vì $g_1 \notin \langle g_2,\ldots,g_m \rangle$ nên theo Mệnh đề 1 thì $$\frac{\partial f_1}{\partial x_s} + \sum_{j=k+1}^m h_{j1} \dfrac{\partial f_j}{\partial x_s} \in I, \qquad s=1,\ldots,n.$$ Theo công thức Euler cho các đa thức thuần nhất $f_j$, ta có $$\deg(f_1)f_1 + \sum_{j=k+1}^m \deg(f_j) h_{j1} f_j = \sum_{s = 1}^n x_s \frac{\partial f_1}{\partial x_s} + \sum_{j=k+1}^m h_{j1} \sum_{s=1}^n x_s \dfrac{\partial f_j}{\partial x_s} \in \langle x_1,\ldots,x_n \rangle I.$$ Mà $I = \langle f_1,\ldots,f_m\rangle$ và các đa thức $h_{j1} f_j$ đều thuần nhất bậc $\deg(f_1)$ nên $$\deg(f_1)f_1 + \sum_{j=k+1}^m \deg(f_j) h_{j1} f_j \in \langle f_2,\ldots,f_m \rangle,$$ suy ra $f_1 \in \langle f_2,\ldots,f_m \rangle$, mâu thuẫn với việc chọn $f_1,\ldots,f_m$ là hệ sinh nhỏ nhất của ideal $I$. Vậy $f_1,\ldots,f_m$ độc lập đại số và chứng minh kết thúc. $\square$

Ta chuyển qua chứng minh điều kiện cần. Xét $G \subseteq \text{GL}_n(\mathbb{C})$ là một nhóm ma trận hữu hạ bất kỳ (không nhất thiết sinh bởi các phép giả phản xạ). Ta tìm khai triển Laurent cho chuỗi Hilbert $\Phi_G(t)$ của $\mathbb{C}[x_1,\ldots,x_n]^G$. Nhắc lại công thức Molien $$\Phi_G(t) = \frac{1}{|G|} \sum_{\sigma \in G} \frac{1}{\det(\text{id} - t\sigma)}.$$

• Với $\sigma = \text{id}$, ta có $\frac{1}{\det(\text{id} - t\text{id})} = \frac{1}{(1-t)^n}$.
• Với $\sigma \in G$ là một phép giả phản xạ thì $\sigma$ có giá trị riêng $1$ với bội $n-1$ và một giá trị riêng đơn $\lambda \neq 1$. Khi đó $\frac{1}{\det(\text{id} - t\sigma)} = \frac{1}{(1-t)^{n-1}(1 - \lambda t)}$. Mặt khác, $\sigma^{-1}$ cũng là một phép giả phản xạ và $\frac{1}{\det(\text{id} - t\sigma^{-1})} = \frac{1}{(1-t)^{n-1}(1 - \lambda^{-1} t)}$, do đó $$\begin{align*} \frac{1}{\det(\text{id} - t\sigma)} + \frac{1}{\det(\text{id} - t\sigma^{-1})} & = \frac{1}{(1-t)^{n-1}}\left(\frac{1}{1 - \lambda t} + \frac{1}{1 - \lambda^{-1} t}\right) \\ &= \frac{1}{(1-t)^{n-1}}\left(\frac{1}{1 - \lambda} +  \frac{1}{1 - \lambda^{-1}} + O(1-t)\right) \\ & = \frac{1}{(1-t)^{n-1}} + O((1-t)^{2-n}) \end{align*}.$$ Vì thế khi lấy tổng của $\frac{1}{\det(\text{id} - t\sigma)}.$ trên các phép giả phản xạ $\sigma \in G$, ta thu được $\frac{r}{2(1-t)^{n-1}} + O((1-t)^{2-n})$, với $r$ là số phép giả phản xạ trong $G$.
• Trong các trường hợp còn lại, giá trị riêng $1$ của $\sigma$ có bội $\le n-2$, nên $\frac{1}{\det(\text{id} - t\sigma)} = O((1-t)^{2-n})$.

Tóm lại $$\phi_G(t) = \frac{1}{|G|(1-t)^n} + \frac{r}{2|G|(1-t)^{n-1}} + O((1-t)^{2-n}).$$

Chứng minh điều kiện cần trong định lý Chevalley-Shephard-Todd. Giả sử $\mathbb{C}[x_1,\ldots,x_n]^G = \mathbb{C}[\theta_1,\ldots,\theta_n]$ là một đại số đa thức, trong đó $\theta_1,\ldots,\theta_n$ độc lập đại số và thuần nhất với bậc lần lượt là $d_1,\ldots,d_n$. Chuỗi Hilbert của nó được cho bởi $$\begin{align*} \Phi_G(t) & = \dfrac{1}{(1 - t^{d_1}) \cdots (1 - t^{d_n})} \\ & = \left(\frac{1}{d_1(1-t)} + \frac{d_1-1}{2d_1} + O(1-t) \right) \cdots \left(\frac{1}{d_n(1-t)} + \frac{d_n-1}{2d_n} + O(1-t) \right) \\ & = \frac{1}{d_1 \cdots d_n(1-t)^n} + \frac{d_1 + \cdots + d_n - n}{2d_1 \cdots d_n(1-t)^{n-1}} + O((1-t)^{2-n}) \end{align*},$$ do đó $|G| = d_1 \cdots d_n$ và $r = d_1 + \cdots + d_n - n$, với $r$ là số phép giả phản xạ trong $G$.

Ký hiệu bởi $H$ nhóm con của $G$ sinh bởi các phép giả phản xạ. Từ điều kiện cần, ta biết rằng $\mathbb{C}[x_1,\ldots,x_n]^H = \mathbb{C}[\psi_1,\ldots,\psi_n]$ là một đại số đa thức, trong đó $\psi_1,\ldots,\psi_n$ độc lập đại số và thuần nhất với bậc lần lượt là $e_1,\ldots,e_n$. Hiển nhiên ta cũng có $|H| =  e_1 \cdots e_n$ và $r = e_1 + \cdots + e_n - n$, suy ra $d_1 + \cdots + d_n = e_1 + \cdots + e_n$.

Vì $\mathbb{C}[x_1,\ldots,x_n]^G \subseteq \mathbb{C}[x_1,\ldots,x_n]^H$ nên mỗi bất biến $\theta_i$ là một hàm đa thức theo $\psi_1,\ldots,\psi_n$. Theo tiêu chuẩn Jacobi về độc lập đại số (xem https://www.scienced...19566988371022X), ma trận $\left[\dfrac{\partial \theta_i}{\partial \psi_j} \right]$ có định thức (xem như phần tử của $\mathbb{C}[\psi_1,\ldots,\psi_n]$) khác $0$. Nói riêng, tồn tại hoán vị $\sigma \in S_n$ sao cho $\dfrac{\partial \theta_{\sigma(i)}}{\partial \psi_i} \neq 0$ với $i=1,\ldots,n$, nghĩa là $\psi_i$ xuất hiện trong $\theta_{\sigma(i)}$. Nói riêng, $e_i \le d_{\sigma(i)}$. Mà $e_1 + \cdots + e_n = d_1 + \cdots + d_n$ nên $e_i = d_{\sigma(i)}$ với $i=1,\ldots,n$, từ đó $|H| = e_1 \cdots e_n = d_1 \cdots d_n = |G|$, nên $G = H$ được sinh bởi các phép giả phản xạ. $\square$

4 - TÍNH COHEN-MACAULEY

Trong trường hợp $G = S_n$ là nhóm đối xứng (nhóm các ma trận hoán vị), ta biết rằng $\mathbb{C}[x_1,\ldots,x_n]^{S_n}$ là một đại số đa thức (sinh bởi các đa thức đối xứng sơ cấp). Với nhóm ma trận hữu hạn $G$ tùy ý thì điều này không còn đúng, tuy nhiên ta có một tính chất gần tốt như vậy, nó cho ta một phân tích tương đối đơn giản của đại số con bất biến.

Cho $R$ là một $\mathbb{C}$-đại số phân bậc với chiều Krull bằng $n$. Ký hiệu bởi $R_d$ thành phần thuần nhất bậc $d$ của $R$ với mỗi $d \ge 0$. Theo bổ đề chuẩn hóa Noether, tồn tại $n$ đa thức thuần nhất bậc dương $\theta_1,\ldots,\theta_n \in R$ sao cho $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module hữu hạn sinh (nói riêng, $\theta_1,\ldots,\theta_n$ độc lập đại số). Một hệ $\{\theta_1,\ldots,\theta_n\}$ như vậy được gọi là một hệ tham số thuần nhất của $R$.

Định lý - Định nghĩa. Hai điều kiện sau đây là tương đương.

1. Với một hệ tham số thuần nhất $\{\theta_1,\ldots,\theta_n\}$ nào đó, $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module tự do (hạng hữu hạn).
2. Với mọi hệ tham số thuần nhất $\{\theta_1,\ldots,\theta_n\}$, $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module tự do (hạng hữu hạn).

Nếu một trong hai (vì thế, cả hai) điều kiện trên được thỏa mãn, ta gọi $R$ là một vành Cohen-Macauley.

Khi $R$ là một vành Cohen-Macauley và $\theta_1,\ldots,\theta_n$ là một hệ tham số thuần nhất, các phần tử $\eta_1,\ldots,\eta_k \in R$ tạo thành một cơ sở của $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module $R$ khi và chỉ khi chúng tạo thành một cơ sở của $\mathbb{C}$-không gian vector $R  / \left\langle\theta_1,\ldots,\theta_n\right\rangle$. Phân tích $$R = \bigoplus_{i=1}^k \eta_i \mathbb{C}[\theta_1,\ldots,\theta_n]$$ được gọi là phân tích Hironaka của vành Cohen-Macauley $R$.

Tổng quát hơn, một dãy phần tử $\theta_1,\ldots,\theta_n$ của $R$ được gọi là dãy chính quy nếu $\theta_i$ không phải ước của $0$ trong vành thương $R / \left\langle \theta_1,\ldots,\theta_{i-1} \right\rangle$ với $i=1,\ldots,n$. Giả sử $\{\theta_1,\ldots,\theta_n\}$ là một hệ tham số thuần nhất. Khi đó nó là một dãy chính quy khi và chỉ khi $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module tự do. Thật vậy, nếu $\theta_1,\ldots,\theta_n$ là một dãy chính quy, chọn các phần tử $\eta_1,\ldots,\eta_k \in R$ sao cho chúng tạo thành một cơ sở của $\mathbb{C}$-không gian vector $R  / \left\langle\theta_1,\ldots,\theta_n\right\rangle$. Thế thì $$R = \sum_{i=1}^k \eta_i \mathbb{C}[\theta_1,\ldots,\theta_n]$$ là một tổng trực tiếp (xét một ràng buộc $\mathbb{C}[\theta_1,\ldots,\theta_n]$-tuyến tính tùy ý rồi chiếu nó xuống thương bởi ideal $\left\langle \theta_1,\ldots,\theta_{i-1} \right\rangle$). Ngược lại, nếu $\eta_1,\ldots,\eta_k \in R$ là một cơ sở của $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module $R$ thì $\theta_1$ không phải là ước của $0$ trong $R$. Lý do là vì nếu $\theta_1 g = 0$ với $g \in R$ nào đó, ta có thể viết $g = \eta_1 f_1 + \cdots + \eta_k f_t$, với $f_1,\ldots,f_t \in \mathbb{C}[\theta_1,\ldots,\theta_n]$. Thế thì điều kiện $\theta_1 g = 0$ trở thành $\theta_1 f_1 = \cdots = \theta_1 f_t = 0$ (vì tính tự do của hệ $\eta_1,\ldots,\eta_k$), hay $f_1 = \cdots = f_t = 0$ (vì tất cả đã ở trong vành đa thức $n$ biến $\mathbb{C}[\theta_1,\ldots,\theta_n]$).

Để chứng minh định lý trên, ta cần 2 bổ đề sau đây.

Bổ đề 1. Cho $a_1,\ldots,a_n$ là các số nguyên dương.

1. Một hệ $\{\theta_1,\ldots,\theta_n\}$ là hệ tham số thuần nhất khi và chỉ khi hệ $\{\theta_1^{a_1},\ldots,\theta_n^{a_n}\}$ cũng vậy.
2. Giả sử $\{\theta_1,\ldots,\theta_n\}$ là một hệ tham số thuần nhất. Khi đó $\theta_1,\ldots,\theta_n$ là dãy chính quy khi và chỉ khi $\theta_1^{a_1},\ldots,\theta_n^{a_n}$ cũng vậy.

Chứng minh. Ta có thể giả sử $\theta_1,\ldots,\theta_n$ thuần nhất và độc lập đại số. Dễ thấy $\mathbb{C}[\theta_1,\ldots,\theta_n]$ là một $\mathbb{C}[\theta_1^{a_1},\ldots,\theta_n^{a_n}]$-module tự do với hạn $a_1\cdots a_n$ và cơ sở $$\{\theta_1^{b_1},\ldots,\theta_n^{b_n} : \forall i = 1,\ldots,n, 0 \le b_i < a_i\}.$$ Từ đó ta có cả 1. và 2. $\square$

Bổ đề 2. Cho $\{\theta_1,\ldots,\theta_n\}$ và $\{\phi_1,\ldots,\phi_n\}$ là các hệ tham số thuần nhất. Khi đó tồn tại một tổ hợp $\mathbb{C}$-tuyến tính $\theta = \lambda_1 \theta_1 + \cdots + \lambda_n \theta_n$ sao cho $\{\phi_1,\ldots,\phi_{n-1},\theta\}$ là một hệ tham số thuần nhất.

Chứng minh. Đặt $S = R/\left \langle \phi_1,\ldots,\phi_{n-1} \right \rangle$ và ký hiệu bởi $T$ ảnh của $\mathbb{C}[\theta_1,\ldots,\theta_n]$ trong $S$. Vì $\phi_1,\ldots,\phi_{n-1}$ độc lập đại số nên $S$ có chiều Krull $1$. Vì $S$ là một $T$-module hữu hạn sinh nên $T$ cũng có chiều Krull bằng $1$. Theo bổ đề chuẩn hóa Noether, tồn tại một tổ hợp $\mathbb{C}$-tuyến tính $\theta = \lambda_1 \theta_1 + \cdots + \lambda_n \theta_n$ đồng thời là một tham số thuần nhất của  $T$. Vì $T$ là một $\mathbb{C}[\theta]$-module hữu hạn sinh nên $S$ cũng vậy, suy ra $R$ là một $\mathbb{C}[\phi_1,\ldots,\phi_{n-1},\theta]$-module hữu hạn sinh, hay $\{\phi_1,\ldots,\phi_{n-1},\theta\}$ là một hệ tham số thuần nhất của $R$. $\square$

Chứng minh định lý. Hiển nhiên $2. \Rightarrow 1.$ Ngược lại, giả sử ta có các hệ tham số thuần nhất $\{\theta_1,\ldots,\theta_n\}$ và $\{\phi_1,\ldots,\phi_n\}$, trong đó $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module tự do, hay $\theta_1,\ldots,\theta_n$ là một dãy chính quy. Ta cần chứng minh rằng $\phi_1,\ldots,\phi_n$ cũng là một dãy chính quy. Quy nạp theo $n$ (chiều Krull của $R$).

• Với $n = 1$. Ta có một phần tử chính quy $\theta \in R$ và một tham số thuần nhất $\phi \in R$. Nếu $\phi$ không chính quy thì $\phi u = 0$ với $u \in R \setminus \{0\}$ nào đó. Vậy $\phi$ nằm trong ideal linh tử $\text{Ann}(u)$ của $R$, suy ra $R / \text{Ann}(u)$ có chiều Krull bằng $0$, tức là một vành Artin. Từ đó $\theta^m \in \text{Ann}(u)$ với $m$ đủ lớn, suy ra $\theta^m$ là ước của $0$, mâu thuẫn với Bổ đề 1. Vậy $\phi$ chính quy.
• Xét $n > 1$. Theo Bổ đề 1, ta có thể giả sử rằng $\theta_1,\ldots,\theta_n$ có cùng bậc. Lấy $\theta$ như ở Bổ đề 2 ($\{\phi_1,\ldots,\phi_{n-1},\theta\}$ là một hệ tham số thuần nhất). Ta có thể giả sử $\theta_1,\ldots,\theta_{n-1},\theta$ là $\mathbb{C}$-độc lập tuyến tính (đánh số lại nếu cầu thiết). Thế thì $\theta_1,\ldots,\theta_{n-1},\theta$ là một dãy chính quy trong $R$, hay $R$ là một $\mathbb{C}[\theta_1,\ldots,\theta_{n-1},\theta]$-module tự do. Từ đó suy ra $S = R / \langle \theta \rangle$ là một $\mathbb{C}[\theta_1,\ldots,\theta_{n-1}]$-module tự do. Mặt khác, $\{\phi_1,\ldots,\phi_{n-1}\}$ là một hệ tham số thuần nhất của $S$ nên nên theo giả thiết quy nạp (chiều Krull của $S$ bằng $n-1$) thì $S$ cũng là một $\mathbb{C}[\phi_1,\ldots,\phi_{n-1}]$-module tự do. Từ đây suy ra $R$ là một $\mathbb{C}[\phi_1,\ldots,\phi_{n-1},\theta]$-module tự do, hay $\{\phi_1,\ldots,\phi_{n-1},\theta\}$ là một dãy chính quy trong $R$. Nói riêng, $\theta$ không là ước của $0$, hay chính quy trong $T = R / \langle \phi_1,\ldots,\phi_{n-1} \rangle$ (một vành có chiều Krull bằng 1). Theo trường hợp $n = 1$ thì $\phi_n$ cũng chính quy trong $T$ (vì nó là một tham số thuần nhất). Vậy $T$ là một $\mathbb{C}[\phi_n]$-module tự do, suỷa $R$ là một $\mathbb{C}[\phi_1,\ldots,\phi_n]$-module tự do. $\square$

Giả sử $R$ là vành Cohen-Macauley với phân tích Hironaka $$R = \bigoplus_{i=1}^k \eta_i \mathbb{C}[\theta_1,\ldots,\theta_n],$$ trong đó có thể chọn $\eta_1,\ldots,\eta_k$  thuần nhất. khi đó ta dễ dàng tính được chuỗi Hilbert của $R$ bởi công thức $$\sum_{d = 0}^\infty \dim(R_d)t^d = \frac{t^{\deg(\eta_1)} + \cdots + t^{\deg(\eta_k)}}{(1 - t^{\deg(\theta_1)}) \cdots (1 - t^{\deg(\theta_n)})}.$$

Bây giờ ta chứng minh định lý chính của mục này.

Định lý. Cho $G \subseteq \text{GL}_n(\mathbb{C})$ là một nhóm ma trận hữu hạn. Đại số con bất biến $\mathbb{C}[x_1,\ldots,x_n]^G$  là một vành Cohen-Macauley.

Chứng minh. Nhắc lại rằng $\mathbb{C}[x_1,\ldots,x_n]$ là một mở rộng nguyên của $\mathbb{C}[x_1,\ldots,x_n]^G$, vì thế là một $\mathbb{C}[x_1,\ldots,x_n]^G$-module hữu hạn sinh. Ta có phân tích $$\mathbb{C}[x_1,\ldots,x_n] = \mathbb{C}[x_1,\ldots,x_n]^G \oplus U,$$ với $U = \{f \in \mathbb{C}[x_1,\ldots,x_n]: f = 0\}$ là hạch của toán tử Reynolds. Chiều Krull của $\mathbb{C}[x_1,\ldots,x_n]^G$ bằng $n$, nên nó có một hệ tham số thuần nhất $\{\theta_1,\ldots,\theta_n\}$ theo bổ đề chuẩn hóa Noether. Hiển nhiên đó cũng là một hệ tham số thuần nhất của $\mathbb{C}[x_1,\ldots,x_n]$.

Vành $\mathbb{C}[x_1,\ldots,x_n]$ đương nhiên là Cohen-Macauley, nên nó là một $\mathbb{C}[\theta_1,\ldots,\theta_n]$-module tự do (hạng hữu hạn). Từ đó ta có tổng trực tiếp $$\mathbb{C}[x_1,\ldots,x_n]/\langle \theta_1,\ldots,\theta_n \rangle \cong (\mathbb{C}[x_1,\ldots,x_n]^G / \langle \theta_1,\ldots,\theta_n \rangle) \oplus (U / \langle \theta_1,\ldots,\theta_n \rangle)$$ của các $\mathbb{C}$-không gian vector hữu hạn chiều. Chọn các đa thức thuần nhất $\eta_1,\ldots,\eta_k,\eta_{k+1},\ldots,\eta_s$ sao cho $\eta_1,\ldots,\eta_k$ là một cơ sở của $\mathbb{C}$-không gian vector $\mathbb{C}[x_1,\ldots,x_n]^G / \langle \theta_1,\ldots,\theta_n \rangle$ và $\eta_{k+1},\ldots,\eta_s$ là một cơ sở của $\mathbb{C}$-không gian vector $U / \langle \theta_1,\ldots,\theta_n \rangle$. Từ đây ta có phân tích Hironaka $$\mathbb{C}[x_1,\ldots,x_n] = \bigoplus_{i=1}^{s} \eta_i \mathbb{C}[\theta_1,\ldots,\theta_n],$$ suy ra $$\mathbb{C}[x_1,\ldots,x_n]^G = \bigoplus_{i=1}^{k} \eta_i \mathbb{C}[\theta_1,\ldots,\theta_n],$$ nên $\mathbb{C}[x_1,\ldots,x_n]^G$ là một vành Cohen-Macauley. $\square$

Trong phân tích Hironaka của $\mathbb{C}[x_1,\ldots,x_n]^G$ như trên, các tham số thuần nhất $\theta_1,\ldots,\theta_n$ được gọi là các bất biến sơ cấp. Các phần tử sinh (thuần nhất) $\eta_1,\ldots,\eta_k$ được gọi là các bất biến thứ cấp. Lần lượt ký hiệu bậc của chúng bởi $d_1,\ldots,d_n$ và $e_1,\ldots,e_k$. Chuỗi Hilbert của $\mathbb{C}[x_1,\ldots,x_n]^G$ khi đó được cho bởi công thức $$\Phi_G(t) = \frac{t^{e_1} + \cdots + t^{e_k}}{(1 - t^{d_1})\cdots(1 - t^{d_n})}.$$ So sánh đẳng thức trên với công thức Molien, ta được $$\frac{t^{e_1} + \cdots + t^{e_k}}{(1 - t^{d_1})\cdots(1 - t^{d_n})} = \frac{1}{|G|}\sum_{\sigma \in G} \frac{1}{\det(\text{id} - t\sigma)}.$$ Nhân hai vế với $(1 - t)^n$ và tính giá trị hai vế tại $t = 1$, ta được $$\frac{k}{d_1 \cdots d_n} = \frac{1}{|G|},$$ vì ở vế phải, trừ ma trận đơn vị có $\det(\text{id} - t\text{id}) = (1-t)^n$ thì bội của giá trị riêng $1$ của các phần tử khác đều nhỏ hơn $n$. Từ đây ta thấy $k = \dfrac{d_1 \cdots d_n}{|G|}$, nghĩa là số bất biến thứ cấp chỉ phụ thuộc vào bậc của các bất biến sơ cấp.

1 - GIỚI THIỆU

Một định lý quen thuộc nói rằng mọi đa thức đối xứng đều biểu diễn được (một cách duy nhất) dưới dạng hàm đa thức theo các đa thức đối xứng sơ cấp. Cụ thể, nếu ta xét tác động hiển nhiên của nhóm đối xứng $S_n$ trên đại số đa thức $K[x_1,\ldots,x_n]$ (với $K$ là một trường tùy ý) thì ta có đẳng cấu đại số $$K[y_1,\ldots,y_n] \to K[x_1,\ldots,x_n]^{S_n} := \{f \in K[x_1,\ldots,x_n]: \forall \sigma \in S_n, \sigma \cdot f = f\}$$ $$y_i \mapsto e_i,$$ trong đó $e_i$ là đa thức đối xứng sơ cấp thứ $i$, được định nghĩa bởi $$\begin{align*} e_1 & = x_1 + \cdots + x_n, \\ e_2 & = \sum_{1 \le i < j \le n} x_i x_j, \\ \vdots \\ e_n & = x_1\cdots x_n.\end{align*}$$

Dễ thấy trong trường hợp trên, nhóm $S_n$ tác động lên $K[x_1,\ldots,x_n]$ bằng các đẳng cấu $K$-đại số phân bậc. Lý thuyết bất biến của nhóm hữu hạn quan tâm đến bài toán tổng quát: cho $G$ là một nhóm ma trận hữu hạn (một nhóm con của $\text{GL}_n(K)$), nó tác động lên không gian các đa thức thuần nhất bậc 1 (sinh bởi $x_1,\ldots,x_n$), vì thế tác động lên $K[x_1,\ldots,x_n]$ một cách tự nhiên. Ta biết gì về đại số con bất biến $K[x_1,\ldots,x_n]^G$?

Về mặt tính toán toán, người ta quan tâm đến các câu hỏi sau.

1. Tìm một hệ sinh (theo nghĩa $K$-đại số) $f_1,\ldots,f_m$ cho $K[x_1,\ldots,x_n]^G$, tức là ta có toàn cấu $$K[y_1,\ldots,y_m] \to K[x_1,\ldots,x_n]^G, \qquad y_i \mapsto f_i.$$ (Ta sẽ thấy rằng hệ sinh như vậy luôn tồn tại theo định lý hữu hạn Hilbert, và kết quả vẫn đúng nếu thay điều kiện $G$ hữu hạn bằng reductive. Ngược lại, khi $G$ không reductive thì Nagata đã đưa ra một ví dụ nổi tiếng rằng đại số $K[x_1,\ldots,x_n]^G$ không nhất thiết hữu hạn sinh).
2. Giả sử $f_1,\ldots,f_m$ là một hệ sinh của $K[x_1,\ldots,x_n]^G$, tìm quan hệ đại số giữa các phần tử sinh $f_i$ (các đa thức $g_1,\ldots,g_k \in K[y_1,\ldots,y_m]$ sao cho $g_1(f_1,\ldots,f_m) = \ldots = g_k(f_1,\ldots,f_m) = 0$, các syzygy), tức là ta có đẳng cấu $$K[y_1,\ldots,y_m] / \left\langle g_1,\ldots,g_m \right\rangle \cong K[x_1,\ldots,x_n]^G, \qquad y_i \mapsto f_i.$$ (Tồn tại một hệ hữu hạn syzygy theo định lý cơ sở Hilbert).
3. Cho một đa thức bất biến $f \in K[x_1,\ldots,x_n]^G$, mô tả $f$ dưới dạng hàm đa thức theo các phần tử sinh, tức là tìm đa thức $g \in K[y_1,\ldots,y_m]$ sao cho $f = g(f_1,\ldots,f_m)$.

Các bài toán trên đều có lời giải bằng cách dùng cơ sở Gröbner.

Ở bài này, mình đề cập đến một số tính  Để đơn giản, người ta thường xét trường hợp $K$ là một trường đóng đại số với đặc số 0, ký hiệu bởi $\mathbb{C}$. $G$ luôn là một nhóm con hữu hạn của $\text{GL}_n(\mathbb{C})$.

2 - TÍNH HỮU HẠN SINH

Ở mục này, ta chứng minh

Định lý hữu hạn Hilbert. $\mathbb{C}[x_1,\ldots,x_n]^G$ là một $\mathbb{C}$-đại số hữu hạn sinh.

Trước hết, nhận xét rằng chiều Krull của $K[x_1,\ldots,x_n]^G$ bằng $n$. Thật vậy, thêm biến mới $t$ và xét các đa thức ẩn $t$ $$P_i(t) = \prod_{\sigma \in G} (t - g \cdot x_i)$$ với $i = 1,\ldots,n$. Dễ thấy $P_i \in \mathbb{C}[x_1,\ldots,x_n]^G[t]$, $P_i$ là đa thức đơn khởi (monic) và $t = x_i$ là một nghiệm của $t$. Vậy $\mathbb{C}[x_1,\ldots,x_n]$ là một mở rộng nguyên của $\mathbb{C}[x_1,\ldots,x_n]^G$ (hay $\mathbb{C}(x_1,\ldots,x_n)$ là một mở rộng đại số của trường các thương của $\mathbb{C}[x_1,\ldots,x_n]^G$).

Ý tưởng ở trên là xuất phát từ đa thức $t - x_i$, sau đó lấy tích của các $\sigma \cdot (t - x_i) = t - \sigma \cdot x_i$ với $\sigma \in G$ để thu được một phần tử của $\mathbb{C}[x_1,\ldots,x_n]^G[t]$. Điều này gợi ý rằng việc lấy tích (hoặc tổng, hoặc trung bình...) theo $G$-quỹ đạo là một thao tác tự nhiên để thu được các đa thức bất biến.

Định nghĩa. Toán tử Reynolds $(-)^\ast: \mathbb{C}[x_1,\ldots,x_n] \to \mathbb{C}[x_1,\ldots,x_n]$ được định nghĩa bởi $$f \mapsto f^\ast := \frac{1}{|G|}\sum_{\sigma \in G} \sigma \cdot f.$$

Dễ thấy toán tử Reynolds thỏa mãn các tính chất sau.

1. $f^\ast \in f \in \mathbb{C}[x_1,\ldots,x_n]^G$ với mọi $f \in f \in \mathbb{C}[x_1,\ldots,x_n]$ và $f^\ast = f$ với mọi $f \in \mathbb{C}[x_1,\ldots,x_n]^G$, tức là $(-)^\ast$ là một phép chiếu lên $\mathbb{C}[x_1,\ldots,x_n]^G$).
2. $(fg)^\ast = f g^\ast$ với mọi $f \in \mathbb{C}[x_1,\ldots,x_n]^G$ và $g \in \mathbb{C}[x_1,\ldots,x_n]$, tức là $(-)^\ast$ là một đồng cấu $\mathbb{C}[x_1,\ldots,x_n]^G$-module.

Trong các chứng minh về sau, ta chỉ cần sử dụng 2 tính chất này của toán tử Reynolds. Nếu $G \subseteq \text{GL}_n(\mathbb{C})$ là một nhóm Lie compact (nói riêng, nó reductive) thì ta có thể định nghĩa $$f^\ast: = \int_G (\sigma \cdot f) d\sigma,$$ với $d\sigma$ là độ đo xác suất Haar trên $G$. Toán tử $(-)^\ast$ cũng thỏa mãn 2 tính chất trên nên nó sẽ đóng vai trò như toán tử Reynolds trong trường hợp $G$ hữu hạn.

Chứng minh Định lý hữu hạn Hilbert. Xét $I$ là ideal của $\mathbb{C}[x_1,\ldots,x_n]$ sinh bởi các đa thức bất biến thuần nhất bậc dương. Theo định lý cơ sở Hilbert, tồn tại các đa thức bất biến thuần nhất bậc dương $f_1,\ldots,f_m \in \mathbb{C}[x_1,\ldots,x_n]^G$ sao cho $$I = \left\langle f_1,\ldots,f_m \right\rangle.$$ Ta chứng minh rằng $\mathbb{C}[x_1,\ldots,x_n]^G = \mathbb{C}[f_1,\ldots,f_m]$. Giả sử phản chứng rằng tồn tại $g \in \mathbb{C}[x_1,\ldots,x_n]^G \setminus \mathbb{C}[f_1,\ldots,f_m]$, thế thì ít nhất một thành phần thuần nhất của $g$ cũng không nằm trong $\mathbb{C}[f_1,\ldots,f_m]$, nên ta có thể giả sử $g$ thuần nhất. Chọn $g$ có bậc nhỏ nhất (và thuần nhất) như vậy. Vì $g \in I$ nên ta có thể viết $$g = g_1f_1 + \cdots g_m f_m$$ với $g_1,\ldots,g_m \in \mathbb{C}[x_1,\ldots,x_n]$. So sánh thành phần thuần nhất bậc $\deg(g)$ ở hai vế, ta có thể giả sử rằng mỗi đa thức $g_i$ thuần nhất bậc $\deg(g) - \deg(f_i) < \deg(g)$. Áp dụng toán tử Reynolds lên hai vế, ta được $$g = g_1^\ast f_1 + \cdots + g_m^\ast f_m.$$ Khi đó mỗi đa thức $g_i^\ast$ là bất biến và thuần nhất với bậc $\deg(g_i) < \deg(g)$, nên theo cách chọn $g$ thì $g_1^\ast,\ldots,g_m^\ast \in \mathbb{C}[f_1,\ldots,f_m]$, suy ra $g \in \mathbb{C}[f_1,\ldots,f_m]$, mâu thuẫn. $\square$

Theo chứng minh trên, ta thấy rằng một hệ sinh của ideal $I$ sẽ tự động là một hệ sinh của đại số con $\mathbb{C}[x_1,\ldots,x_n]^G$.

3 - CÔNG THỨC MOLIEN

Ta muốn đếm số bất biến (độc lập tuyến tính) bậc $d$ cho trước. Ta có thể làm điều này bằng các tính chuỗi Hilbert $$\Phi_G(t) = \sum_{d = 0}^\infty \dim(\mathbb{C}[x_1,\ldots,x_n]^G_d) t^d$$ của $\mathbb{C}[x_1,\ldots,x_n]^G$, trong đó $(-)_d$ chỉ thành phần thuần nhất bậc $d$.

Bổ đề. Cho $V$ là một không gian vector và $G$ là một nhóm con hữu han của $\text{GL}(V)$. Ký hiệu bởi $V^G = \{v \in V: \forall \sigma \in G, \qquad \}$ Khi đó $$\dim(V^G) = \frac{1}{|G|}\sum_{\sigma \in G} \text{Tr}(\sigma)$$ ($\text{Tr}$ chỉ vết của tự đồng cấu).

Chứng minh. Xét trung bình hóa $$\pi = \frac{1}{|G|} \sum_{\sigma \in G} \sigma: V \to V.$$ Dễ thấy $\pi(v) \in V^G$ với mọi $v \in V$ và $\pi(v) = v$ với mọi $v \in V^G$. Nói riêng, $\pi^2 = \pi$, hay $\pi$ là phép chiếu lên $V^G$. Vì thế $\pi$ chéo hóa được với các giá trị riêng là $0$ hoặc $1$. Do đó $\dim(V^G) = \text{rank}(\pi) = \text{Tr}(\pi) = \dfrac{1}{|G|}\sum_{\sigma \in G} \text{Tr}(\sigma).$ $\square$
 

Công thức Molien. Chuỗi Hilbert của $\mathbb{C}[x_1,\ldots,x_n]^G$ được cho bởi $$\Phi_G(t) = \frac{1}{|G|}\sum_{\sigma \in G} \frac{1}{\det(\text{id} - t \sigma)}.$$

Chứng minh. Cố định $\sigma \in G$. Với mỗi $d \ge 0$, ta có $\mathbb{C}[x_1,\ldots,x_n]_d = S^d \mathbb{C}[x_1,\ldots,x_n]_1$ (ký hiệu $S^d$ chỉ lũy thừa đối xứng bậc $d$. Ký hiệu $\sigma_d = S^d\sigma: \mathbb{C}[x_1,\ldots,x_n]_d \to \mathbb{C}[x_1,\ldots,x_n]_d$ là tác động của $\sigma$ trên thành phần thuần nhất bậc $d$. Theo bổ đề trên, ta cần tính $\text{Tr}(\sigma_d)$. Vì $\sigma^{|G|} = \text{id}$ nên $\sigma$ chéo hóa được, gọi $v_1,\ldots,v_n$ là một cơ sở của $\mathbb{C}[x_1,\ldots,x_n]_1$ gồm các vector riêng của $\sigma$, với các giá trị riêng tương ứng là $\lambda_1,\ldots,\lambda_n$. Dễ thấy các $\sigma_d$ cũng chéo hóa được: Các vector $$v_{i_1}\cdots v_{i_d},$$ với $(i_1,\ldots,i_d) \in \{1,\ldots,n\}^n$ chạy trên các bộ sao cho $1 \le i_1 \le \cdots \le i_d \le n$, tạo thành một cơ sở của $\mathbb{C}[x_1,\ldots,x_n]_d$ với các giá trị riêng tương ứng $\lambda_{i_1}\cdots \lambda_{i_d}$. Từ đây ta có $$\begin{align*} \sum_{d = 0}^{\infty} \text{Tr}(\sigma_d) & = \sum_{d = 0}^{\infty} \sum_{1 \le i_1 \le \cdots \le i_d \le n} \lambda_{i_1}\cdots \lambda_{i_d}t^d \\ & = (1 + \lambda_1t + \lambda_1^2t^2 + \cdots) \cdots (1 + \lambda_nt + \lambda_n^2t^2 + \cdots) \\ & = \frac{1}{(1 - \lambda_1 t) \cdots (1 - \lambda_n t)} \\ & = \frac{1}{\det(\text{id} - t\sigma)}. \end{align*}$$ Theo bổ đề trên, ta có $$\Phi_G(t) = \sum_{d = 0}^{\infty} \frac{1}{|G|} \sum_{\sigma \in G} \text{Tr}(\sigma_d) = \frac{1}{|G|}\sum_{\sigma \in G} \frac{1}{\det(\text{id} - t\sigma)}.$$ $\square$