Với $x \ge 1$ thì $0 < \frac{\sqrt{x+1}}{x^2} \le \frac{\sqrt{x+x}}{x^2} = \frac{\sqrt{2}}{x\sqrt{x}}$. Mặt khác, tích phân $\int_1^{\infty} \frac{\sqrt{2}}{x\sqrt{x}}$ hội tụ. Thật vậy, $$\lim_{M \to \infty} \int_1^M \frac{\sqrt{2}}{x\sqrt{x}} = \lim_{M \to \infty} \left(-\frac{\sqrt{2}}{2\sqrt{x}} \Bigg|_{x = 1}^{x=M} \right) = \lim_{M \to \infty}\left(\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2M}}\right) = \frac{1}{\sqrt{2}}.$$ Theo tiêu chuẩn so sánh, tích phân đã cho hội tụ.

Một lý thuyết toán học gồm những tiên đề và một hệ thống quy tắc suy luận. Chứng minh toán học là dùng các quy tắc suy luận để đi từ các tiên đề đến các định lý, phát biểu... Các định nghĩa dựa theo những định nghĩa đã có trước. Vì thế phải có những khái niệm nguyên thủy đầu tiên, không định nghĩa (không nói chúng là gì, nhưng chúng phải thỏa mãn những tiên đề của lý thuyết).

 

Hệ tiên đề được sử dụng rộng rãi trong toán học hiện nay là lý thuyết tập hợp ZFC.  Đối tượng nguyên thủy (không định nghĩa) là các tập hợp. Một khái niệm được coi là định nghĩa rõ ràng nếu nó là một tập hợp, một phần tử của một tập hợp nào đó... Hình thức hóa về cơ bản là đưa các khái niệm về lý thuyết tập hợp, sử dụng các mệnh đề toán học (gồm các toán hạng như các số 0,1, 2,..., quan hệ giữa các toán hạng như dấu =, <, >, ..., và các toán tử của logic vị từ "và", "hoặc", "$\implies$", $\iff$,... cũng như hai lượng từ của logic bậc nhất $\forall$, $\exists$.

Chứng minh rằng với mọi số nguyên dương $n$ thì

$$\prod_{k=1}^{n-1} \left(4\cos^2 \tfrac{k\pi}{n} + 1\right) = F_n^2,$$ trong đó $$\begin{cases} F_1 = F_2 = 1, \\ F_n = F_{n-1} + F_{n-2} & \text{nếu } n \ge 3. \end{cases}$$

Giải đấu trên $3$ vận động viên với $3$ người vô địch tương đối.

Giải đấu trên $4$ vận động viên với $3$ người vô địch tương đối.

GIải đấu trên $6$ vận động viên với $6$ người vô địch tương đối.

Ta gọi một “giải đấu” trên $n$ vận động viên là một cách gán thắng/thua cho từng trận đấu (trong tổng cộng $\frac{n(n-1)}{2}$ trận đấu).

Dễ dàng xây dựng giải đấu trên $3$ cũng như $4$ vận động viên sao cho có $3$ vận động viên vô địch tương đối. Do đó $S_3 = 3$ và $S_4 \ge 3$.

Để chứng minh $S_4 < 4$, ta xét một giải đấu tuỳ ý trên $4$ vận động viên.

• Nếu có một vận động viên $a$ thắng cả $3$ trận thì các vận động viên còn lại không thể viết được tên $a$, nên họ đều không vô địch tương đối.
• Nếu có một vận động viên $a$ thua cả $3$ trận thì anh ta không thể viết tên ai, nên không vô địch tương đối.
• Trường hợp còn lại, mỗi vận động viên đều thắng đúng $1$ hoặc $2$ trận. Mà tổng số trận đấu là $6$ nên có đúng $2$ vận động viên chỉ thắng $1$ trận, gọi họ là $a$ và $b$ và giả sử rằng $a$ thắng $b$. Rõ ràng $a$ chỉ viết được tên của $b$ và người duy nhất mà $b$ thắng, nên $a$ không vô địch tương đối.

Tóm lại, không tồn tại giải đấu trên $4$ vận động viên mà cả $4$ đều vô địch tương đối, vậy $S_4 < 4$, hay $S_4 = 3$.

Tiếp theo, ta định nghĩa một “tam giác” là một bộ $3$ vận động viên $a,b,c$ mà $a$ thắng $b$, $b$ thắng $c$ và $c$ thắng $a$. Ta có nhận xét sau: một giải đấu có cả $n$ vận động viên đều vô địch tương đối khi và chỉ khi mỗi cặp vận động viên đều nằm trong một tam giác nào đó.

Từ nhận xét trên, ta chứng minh khẳng định sau: nếu $S_n = n$ thì $S_{n+2} = n+2$. Thật vậy, giả sử tồn tại một giải đấu $n$ vận động viên sao cho cả $n$ người đều vô địch tương đối. Ta thêm hai vận động viên mới là $a$ và $b$, và xây dựng giải đấu mới trên tất cả $n+2$ vận động viên này bằng cách quy định: $a$ thắng $b$, $b$ thắng tất cả $n$ vận động viên cũ, và tất cả vận động viên cũ thắng $a$. Dễ thấy lúc này, mọi cặp vận động viên đều nằm trong một tam giác nào đó, nên ta thu được một giải đấu với $n+2$ vận động viên đều vô địch tương đối.

Từ đó dễ thấy $S_n = n$ với mọi $n \ge 3$ và lẻ.
Ta cũng xây dựng được giải đấu với $6$ vận động viên đều vô địch tương đối, nên $S_6 = 6$, từ đó $S_n = n$ với mọi $n \ge 6$ và chẵn.

Anh có thể nói kĩ về nhận xét được không ạ, nếu mỗi cặp vận động viên đều nằm trong một tam giác thì sẽ có cả $n$ vận động viên vô địch tương đối?

 

Nếu mỗi cặp vận động viên $\{a, b\}$ đều nằm trong một tam giác dạng ($a$ thắng $b$, $b$ thắng $c$, $c$ thắng $a$) hoặc ($b$ thắng $a$, $a$ thắng $c$, $c$ thắng $b$) thì $a$ viết được tên $b$ và $b$ cũng viết được tên $a$. Nếu điều này đúng với mọi cặp vận động viên thì mỗi vận động viên đều viết được tên của $n-1$ vận động viên còn lại, nghĩa là mọi vận động viên đều vô địch tương đối.

Ngược lại, giả sử một giải đấu có cả $n$ vận động viên vô địch tương đối. Xét một cặp vận động viên $\{a,b\}$ tùy ý. Ta có thể giả sử $a$ thắng $b$. Vì $b$ viết được tên $a$ tên tồn tại một vận động viên $c$ mà $b$ thắng $c$ và $c$ thắng $a$, vậy ta thu được tam giác $(a,b,c)$ chứa cặp $\{a,b\}$.

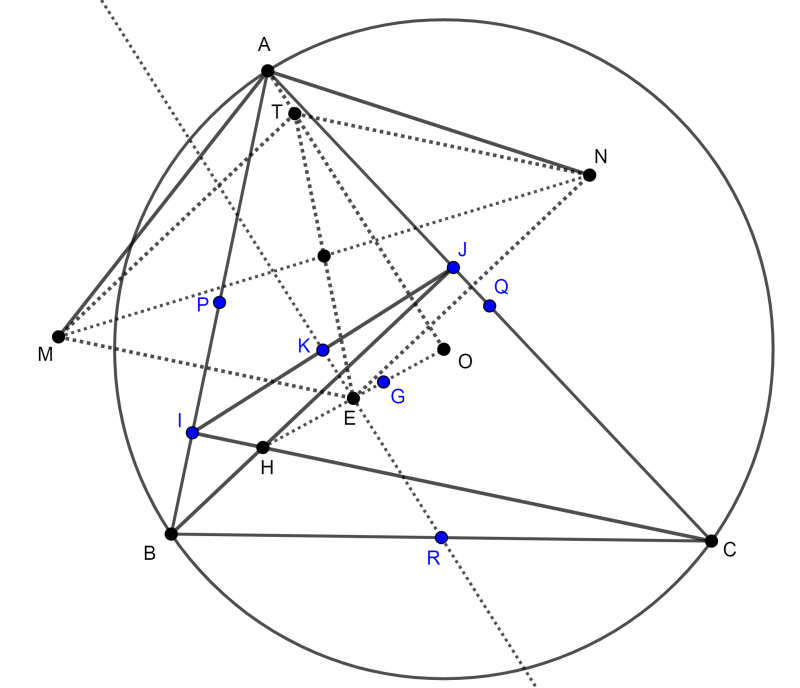
Mình đổi lại tên tâm đường tròn Euler của $\triangle ABC$ là $E$.

 

Cách làm bằng véctơ:

Gọi $I, J$ lần lượt là chân đường cao kẻ từ $B$ và từ $C$ của $\triangle ABC$. Gọi $P, Q, R, K$ lần lượt là trung điểm của $AB, AC, BC, IJ$. Gọi $G$ là trọng tâm $\triangle ABC$.

Ta có $$\overrightarrow{AT} = \overrightarrow{AE} + \overrightarrow{ET} = \frac{1}{2}(\overrightarrow{AO} + \overrightarrow{AH}) + (\overrightarrow{EM} + \overrightarrow{EN})$$ vì $E$ là trung điểm của $OH$, và vì tứ giác $EMTN$ là hình bình hành).

Một mặt, ta có tính chất quen thuộc $\overrightarrow{AH} = 2\overrightarrow{OR}$.

Mặt khác, đường thẳng $EM$ chứa đường trung bình của hình thang $HOPI$ và $M$ đối xứng với $E$ nên $\overrightarrow{EM} = \overrightarrow{OP} + \overrightarrow{HI}$. Tương tự, ta có $\overrightarrow{EN} = \overrightarrow{OQ} + \overrightarrow{HJ}$. Từ đó $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + (\overrightarrow{OR} + \overrightarrow{OP} + \overrightarrow{OQ}) + (\overrightarrow{HI} + \overrightarrow{HJ}).$$ Do $G$ cũng là trọng tâm của $\triangle PQR$ và do $K$ là trung điểm của $IJ$ nên $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + 3\overrightarrow{OG} + 2\overrightarrow{HK}.$$ Cuối cùng, $$3\overrightarrow{OG} = \overrightarrow{OH} = 2\overrightarrow{EH}$$ nên $$\overrightarrow{AT} = \frac{1}{2}\overrightarrow{AO} + 2\overrightarrow{EH} + 2\overrightarrow{HK} = \frac{1}{2}\overrightarrow{AO} + 2\overrightarrow{EK}.$$ Vì $EI = EJ$ nên đường thẳng $EK$ chính là đường trung trực của $IJ$, suy ra $EK \perp IJ$. Bằng tính chất quen thuộc rằng $IJ \perp AO$ (chứng minh chẳng hạn bằng cách cộng góc), ra suy ra $EK \parallel AO$, do đó các véctơ $\overrightarrow{AT}$ và $\overrightarrow{AO}$ cùng phương, hay $A, T, O$ thẳng hàng.

 

Cho $G = \left\langle g \right\rangle \cong \mathbb{Z}$ là nhóm cyclic vô hạn. Ký hiệu $\text{Ext}^n_{\mathbb{C}G}(-,-)$ chỉ hàm tử $\text{Ext}^n$ trong phạm trù các biểu diễn phức hữu hạn chiều của $G$. Liệu ta có $\text{Ext}^n_{\mathbb{C}G}(\mathbb{C},V) = 0$ với mọi biểu diễn $V$ và mọi $n \ge 2$?

Chú ý: đây có thể coi như họ hàng xa của tính chất: nhóm hầu cyclic $\hat{\mathbb{Z}}$ có số chiều đối đồng điều (cohomological dimension) bằng 1.

\begin{align*} \frac{\sqrt[3]{\cos 2x} - \sqrt{\cos x}}{\ln(1 - x^2)} & = \left(\frac{\sqrt[3]{\cos 2x} - 1}{x^2} - \frac{\sqrt{\cos x} - 1}{x^2}\right) \cdot \frac{x^2}{\ln(1 - x^2)} \\ & = \left(\frac{\cos 2x - 1}{\sqrt[3]{\cos^2 2x} + \sqrt[3]{\cos 2x} + 1} \cdot \frac{1}{x^2} - \frac{\cos x - 1}{\sqrt{\cos x} + 1} \cdot \frac{1}{x^2}\right) \cdot  \left(- \frac{\ln(1 - x^2)}{-x^2} \right)^{-1} \\ & = \left(\frac{\cos 2x - 1}{(2x)^2} \cdot \frac{4}{\sqrt[3]{\cos^2 2x} + \sqrt[3]{\cos 2x} + 1} - \frac{\cos x - 1}{x^2} \cdot \frac{1}{\sqrt{\cos x} + 1}\right) \cdot  \left(- \frac{\ln(1 - x^2)}{-x^2} \right)^{-1} \end{align*}

 

Sử dụng các giới hạn cơ bản $$\lim_{x \to 0} \frac{\cos x - 1}{x^2} = \frac{1}{2}, \quad \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1,$$ ta thu được $$I = \left(\frac{1}{2}\cdot\frac{4}{1+1+1} - \frac{1}{2} \cdot \frac{1}{1+1}\right) \cdot (-1)^{-1} = -\frac{5}{12}.$$

 

Dùng tiêu chuẩn tích phân: 

Chuỗi đa cho hội tụ khi và chỉ khi tích phân suy rộng $$\int_{2}^{+\infty} \frac{1}{x (\ln x)^p}\,dx$$ hội tụ. Đổi biến $\ln(x) = t$, tích phân trên trở thành $$\int_{\ln 2}^{+\infty} \frac{1}{t^p}\,dt.$$ Tích phân này hội tụ khi và chỉ khi $p > 1$.

Con lắc đơn không dao động điều hòa. Khi lập phương trình chính xác và không dùng phép làm tròn $\sin x \approx x$, nghiệm của phương trình vi phân thu được có dạng tích phân elliptic, và ta biết rằng tích phân elliptic thì không biểu diễn được dưới dạng hàm sơ cấp: http://ed.quantum-bg...c-integrals.pdf.

Với $n=0$, bài toán không có nghiệm.
Với $n=1$, hiển nhiên tất cả các nghiệm cho bởi $(P(x), Q(x)) = (x-a, x-a-1)$, với $a$ là số nguyên dương tuỳ ý.
Xét $n \ge 2$. Viết $Q(x) = (x-a_1)\cdots (x-a_n)$ với $a_1 \le \cdots \le a_n$ là các số tự nhiên. Nếu $a$ là một nghiệm của $P$ thì $(a-a_1)\cdots (a-a_n) = Q(a) = P(a) - 1 = -1$, suy ra $a-a_i \in \{\pm 1\}$ với mọi $i = 1,\ldots,n$. Mặt khác ta không thể có $a-a_1 = \cdots = a-a_n = 1$, nên tồn tại chỉ số $i$ sao cho $a-a_i = -1$. Mà $a-a_1 \ge \cdots \ge a-a_n$ nên $a-a_n = -1$, hay $a = a_n - 1$, nghĩa là đây là nghiệm duy nhấy của $P$. Vậy $P(x) = (x-a)^n$.
Ta cũng có $Q(x) = (x-a+1)^k (x-a-1)^{n-k}$ với $0 \le k < n$ nào đó. Nếu $n \ge 3$ thì $k \ge 2$ hoặc $n-k \ge 2$. Trong trường hợp thứ nhất thì $Q’(a-1) = 0$, trong trường hợp thứ hai thì $Q’(a+1) = 0$. Nhưng $Q’(x) = P’(x) = n(x-a)^{n-1}$ chỉ có nghiệm duy nhất là $a$, mâu thuẫn. Vậy với $n \ge 3$ thì bài toán không có nghiệm.
Ta chỉ còn trường hợp $n = 2$. Lúc này, thử trực tiếp $k = 0$ và $k = 1$, ta thấy tất cả các nghiệm của bài toán là $(P(x), Q(x)) = ((x-a)^2, (x-a+1)(x-a-1))$, với $a$ là số nguyên dương tuỳ ý.

Với ý tưởng ở Bước 4, ta có thể tính được biểu thức tường minh cho $f(n)$ như sau.

 

Đặt $m = \left\lfloor \sqrt{n} \right  \rfloor$, $n = m^2 + k$ với $0 \le k \le 2m$. Ta chứng minh bằng quy nạp theo $m$ rằng $\begin{equation} \label{eq:4} f(n+1) - f(n) = \begin{cases} 2(m-k) & \text{nếu } 0 \le k \le m-1, \\ 2(2m-k) + 1 & \text{nếu } m \le k \le 2m. \end{cases} \end{equation}$

Với $m = 1$ thì $\eqref{eq:4}$ đúng vì $f(2) - f(1) = 2$ $(k = 0)$, $f(3) - f(2) = 3$ $(k = 1)$, $f(4) - f(3) = 1$ $(k = 2)$.

Xét $m \ge 2$.

Với $0 \le k \le m-1$ thì $$f(n+1) - f(n) = f(n+1-m) + (n+1) - f(n-m) - n = f(n+1-m) - f(n-m) + 1.$$ Ta có $n-m = (m-1)^2 + (k + (m-1))$, và $m-1 \le k+(m-1) \le 2(m-1)$, nên theo giả thiết quy nạp thì $$f(n+1) - f(n) = f(n+1-m) - f(n-m) + 1 = 2(2(m-1) - (k+(m-1))) + 1 + 1 = 2(m-k).$$

Với $m \le k \le 2m-1$ thì $$f(n+1) - f(n) = f(n+1-m) + (n+1) - f(n-m) - n = f(n+1-m) - f(n-m) + 1.$$ Ta có $n-m = m^2 + (k-m)$, và $0 \le k-m \le m-1$, nên theo trường hợp trước thì $$f(n+1) - f(n) = f(n+1-m) - f(n-m) + 1 = 2(m + (k-m)) + 1 = 2(2m - k) + 1.$$

Với $k = 2m$ thì $$f(n+1) - f(n) = f((m+1)^2) - f(m^2 + 2m) = f(m^2 + m) + (m+1)^2 - (f(m^2 + m) - (m^2+2m)) = 1.$$ Vậy $\eqref{eq:4}$ đúng trong tất cả trường hợp. 

 

Từ đó, với $0 \le k \le m$ thì

$$f(n) = f(m^2 + k) = f(m^2) + \sum_{i=0}^{k-1} 2(m-i) = \frac{m(m+1)(4m-1)}{6} + k(2m-k+1).$$

Với $m+1 \le k \le 2m$ thì $$f(n) = f(m^2 + m) + \sum_{i=0}^{k-1} (2(2m-i) + 1) = \frac{m(m+1)(4m+5)}{6} + k(4m-k+2).$$

 

 

 

Bước 4. Chứng minh rằng $f(n) < f(n+1)$ với mọi $n \in \mathbb{N}^\ast$ bằng quy nạp.

Thật vậy, với $n = 1$ thì $f(2) = 3 > 1 = f(1)$.

Xét $n \ge 2$. Đặt $m = \left\lfloor\sqrt{n}\right\rfloor$. Thế thì $m^2 \le n \le (m+1)^2 - 1$, suy ra $m^2 + \le < n+1 \le (m+1)^2$, nên $n+1 \in \{m,m+1\}$. Suy ra $$f(n+1) = f(n+1-m) + n+1 > f(n-m) + n+1 > f(n-m) + n = f(n)$$ theo giả thiết quy nạp, hoặc $$f(n+1) = f(n+1 - (m+1)) + n + 1 > f(n-m) + n = f(n),$$ vậy $f(n+1) > f(n)$ trong mọi trường hợp, tức là dãy $(f(n))_n$ tăng.

Bước 1. Tính $f(m^2)$ và $f(m^2-m)$.

Với $m \ge 2$, ta có $$\begin{align*} f(m^2) & = f(m^2 - m) + m^2  \\ & = f(m^2 - m - (m-1)) + (m^2 - m) + m^2 \\ & = f((m-1)^2) + 2m^2 - m.\end{align*}$$

Từ đó $\begin{equation} \label{eq:1} f(m^2) = f(1) + \sum_{k=2}^m (2k^2 - k) = \frac{m(m+1)(4m-1)}{6} \end{equation}$ và $\begin{equation} \label{eq:2} f(m^2 - m) = f(m^2) - m^2 = \frac{m(m-1)(4m+1)}{6}. \end{equation}$

 

Bước 2. Đặt $S(m) = \sum_{n=m^2}^{m^2 + 2m} f(n)$ và tính $S(m)$.

Với $m \ge 2$, ta có $$\begin{align*} S(m) & = \sum_{n=m^2}^{m^2 + 2m} f(n) \\ & = \sum_{n=m^2-m}^{m^2 + m} f(n) + \sum_{n=m^2}^{m^2 + 2m} n \\ & = \sum_{n=m^2-m}^{m^2 - 1} f(n) + \sum_{n=m^2}^{m^2 + m} f(n) + m(m+1)(2m+1) \\ & = \sum_{n=(m-1)^2}^{m^2 - m} f(n) + \sum_{n=m^2-m}^{m^2-1} n + \sum_{n=m^2-m}^{m^2} f(n) + \sum_{n=m^2}^{m^2 + m} n + m(m+1)(2m+1) \\ & = \sum_{n=(m-1)^2}^{m^2} f(n) + f(m^2-m) + \sum_{n=m^2-m}^{m^2+m}n + m(m+1)(2m+1) \\ & = S(m-1) + f(m^2) + f(m^2 - m) + m^2(2m+1)  + m(m+1)(2m+1).\end{align*}$$

Kết hợp với $\eqref{eq:1}$ và $\eqref{eq:2}$, ta được $$\begin{align*} S(m) & = S(m-1) + \frac{m(m+1)(4m-1)}{6} + \frac{m(m-1)(4m+1)}{6} + m^2(2m+1) + m(m+1)(2m+1) \\ & = S(m-1) + \frac{16m^3 + 12m^2 + 2m}{3} \end{align*}.$$ Ngoài ra $f(2) = f(1) + 2 = 3$, $f(3) = f(2) + 3 = 6$ nên $S(1) = f(1) + f(2) + f(3) = 10$, suy ra $\begin{equation} \label{eq:3} S(m) = S(1) + \sum_{k=2}^m \frac{16k^3 + 12k^2 + 2k}{3} = \frac{4m^4 + 12m^3 + 11m^2 + 3m}{3}. \end{equation}$

 

Bước 3. Tính $S$.

Sử dụng $\eqref{eq:1}$ và $\eqref{eq:3}$ ta có $$\begin{align*} \sum_{n=1}^{m^2} f(n) & = \sum_{k=1}^{m-1} S(k) + f(m^2) \\ & = \sum_{k=1}^{m-1} \frac{4k^4 + 12k^3 + 11k^2 + 3k}{3} + \frac{m(m+1)(4m-1)}{6} \\ & = \frac{m(m+1)(8m^3 + 2m^2 + 8m-3)}{30}.\end{align*}$$ Thay $m = 10$, ta được $S = \sum_{n=1}^{100} f(n) = 30349$.

 

 

Bước 4. Chứng minh rằng $f(n) < f(n+1)$ với mọi $n \in \mathbb{N}^\ast$ bằng quy nạp.

Thật vậy, với $n = 1$ thì $f(2) = 3 > 1 = f(1)$.

Xét $n \ge 2$. Đặt $m = \left\lfloor\sqrt{n}\right\rfloor$. Thế thì $m^2 \le n \le (m+1)^2 - 1$, suy ra $m^2 + 1 \le n+1 \le (m+1)^2$, nên $n+1 \in \{m,m+1\}$. Suy ra $$f(n+1) = f(n+1-m) + n+1 > f(n-m) + n+1 > f(n-m) + n = f(n)$$ theo giả thiết quy nạp, hoặc $$f(n+1) = f(n+1 - (m+1)) + n + 1 > f(n-m) + n = f(n),$$ vậy $f(n+1) > f(n)$ trong mọi trường hợp, tức là dãy $(f(n))_n$ tăng.

 

Bước 5. Tính $\lim_{n \to +\infty} \frac{f(n)}{n\sqrt{n}}$.

 Đặt $m = \left\lfloor\sqrt{n}\right\rfloor$. Thế thì $m^2 \le n < (m+1)^2$ và $m \to +\infty$ khi $n \to +\infty$. Sử dụng $\eqref{eq:1}$, ta có $$\lim_{m \to +\infty} \frac{f(m^2)}{(m+1)^3} = \lim_{m \to +\infty} \frac{m(4m-1)}{6(m+1)^2} = \frac{2}{3},$$ $$\lim_{m \to +\infty} \frac{f((m+1)^2)}{m^3} = \lim_{m \to +\infty} \frac{(m+1)(m+2)(4m+3)}{6m^3} = \frac{2}{3}.$$ Ngoài ra vì $(f(n))_n$ tăng nên $$\frac{f(m^2)}{(m+1)^3} \le \frac{f(n)}{n\sqrt{n}} \le \frac{f((m+1)^2)}{m^3},$$ suy ra $$\lim_{n \to +\infty} \frac{f(n)}{n\sqrt{n}} = \frac{2}{3}.$$

Bài không khó nhưng hệ số tìm được làm một số quan trọng và xuất hiện trong nhiều bài toán đếm khác nhau. 

Trường hợp riêng của định lý tương ứng Lucas

Điều kiện cần:

Giả sử $n$ thỏa mãn tính chất đã phát biểu. Với $x = p+1$ thì dễ thấy $p \, | \, (p+1)^n - 1$ nên ta phải có $p^2 \, | \, (p+1)^n - 1$.

Dùng nhị thức Newton ta thấy $(p+1)^n \equiv 1 + np \pmod{p^2}$, suy ra $p^2 \,|\, np$, hay $p \,|\, n$.

 

Điều kiện đủ:

Giả sử $p \, | \,n$. Viết $n = kp$. Giả sử $p \,|\, x^n-1$. Theo định lý nhỏ Fermat $$1 \equiv x^n \equiv x^{kp} \equiv x^k \pmod p.$$ Ta có $$x^n - 1 = x^{kp} - 1 = (x^k - 1)(x^{k(p-1)} + x^{k(p-2)} + \cdots + x^k + 1),$$ mà $x^k - 1 \equiv 0 \pmod p$ và $x^{k(p-1)} + x^{k(p-2)} + \cdots + x^k + 1 \equiv 1 + 1 + \cdots + 1 \equiv p \equiv 0 \pmod p$ nên $p^2 \,|\, x^n - 1$.

 

Vậy tất cả số tự nhiên thỏa mãn đề bài là các số tự nhiên chia hết cho $p$.

$$\begin{align*} C^n_{2n} & = (n+1 - n)C^n_{2n} = (n+1)C^n_{2n} - nC^n_{2n} = (n+1)C^n_{2n} - n \cdot \frac{(2n)!}{n! \cdot n!} \\ & = (n+1)C^n_{2n} - (n+1) \cdot \frac{(2n)!}{(n-1)! \cdot (n+1)!} = (n+1)(C^n_{2n} - C^{n-1}_{2n}). \end{align*}$$

Gọi $d$ là đường phân giác của $\widehat{MIB}$ cũng như của $\widehat{NIC}$ (bằng cộng góc, ta dễ thấy $M, I, C$ thằng hàng và $N, I, B$ thằng hàng). Phép đối xứng qua đường thẳng $d$ biến $B$ thành $M$, biến $C$ thành $N$ và biến $(I)$ thành chính nó. Vì $(I)$ nội tiếp $\triangle ABC$ nên để chứng minh nó nội tiếp $\triangle DMN$ thì ta chỉ cần chứng minh rằng $D$ và $A$ đối xứng với nhau qua $d$.
Thật vậy, một mặt, nếu ký hiệu bởi $r$ bán kính của $(I)$ thì từ chỗ $\widehat{ABI} = 30^\circ$ ta tính được $IA = 2r = ID$.
Mặt khác, $$\widehat{AIM} = \widehat{ACI} + \widehat{CAI} = \frac{\widehat{ACB} + \widehat{BAC}}{2} = \frac{180^\circ - \widehat{ABC}}{2} = 90^\circ - \widehat{IBC} = \widehat{BID}$$ nên $d$ cũng là đường phân giác của $\widehat{AID}$. Từ đó suy ra rằng $A$ và $D$ đối xứng với nhau qua $d$, chính là điều ta muốn.

$B, I, N$ thẳng hàng và $C, I, M$ thẳng hàng.

$M, A, N$ cùng thuộc cung $60^{\circ}$ dựng trên đoạn $BC$.

Tính được $\angle AMB=\angle DBM$, hơn nữa $MA=MB=BD$ suy ra $\triangle MAB=\triangle BMD$. Do đó $MD=BA$.
Chứng minh tương tự $ND=AC$.
Thêm vào đó $MN=BC$ do $\triangle IMN=\triangle IBC$.
Như vậy $\triangle DMN=\triangle ABC$ (c.c.c).

Từ đây ta có $\angle MDN=\angle BAC=60^{\circ}$, dẫn tới $B, D, C$ cùng thuộc cung $60^{\circ}$ dựng trên đoạn $MN$.
Mà $CD=CN$, $BD=BM$ suy ra $IM, IN$ lần lượt là tia phân giác của hai góc $DMN, DNM$.

Từ chỗ $IM$ và $IN$ là hai đường phân giác mới suy ra được $I$ là tâm đường tròn ngoại tiếp $\triangle DMN$, em nghĩ cần nói thêm là “vì $\triangle DMN = \triangle ABC$ nên chúng có cùng bán kính đường tròn nội tiếp” nữa.

Coi $b,c,d$ là hằng số và $a$ là biến. Vế trái là hàm lồi theo $a$ nên đạt GLTN trên biên, vậy ta chỉ cần chứng minh bất đẳng thức khi $a = 0$ hoặc $a = 1$. Tương tự với các biến còn lại, ta thấy GTLN của vế phải đạt được khi $a,b,c,d \in \{0,1\}$. Vậy chỉ cần thử cả 16 trường hợp là đủ.

Vậy thì trình bày lời giải trên theo ngôn ngữ sơ cấp.
Đặt $f(a,b,c,d) = $ vế trái. Ta chứng minh $$f(a,b,c,d) \le (1-a)f(0,b,c,d) + a f(1,b,c,d).$$ Chỗ này sau khi rút gọn thì chỉ còn một biến $a$ thôi, biến đổi tương đương sẽ ra $a^2 \le a$. Từ đó suy ra với $b,c,d$ cố định thì vế trái đạt GTLN khi $a = 0$ hoặc $a = 1$.

Từ giả thiết, ta có $a_{n+1}^\alpha = a_n + a_n^\alpha$. Từ đó dãy $(a_n)$ tăng. Nếu nó bị chặn trên thì có giới hạn hữu hạn $\ell$. Nhưng từ đẳng thức trên ta tính được $\ell = 0$, mâu thuẫn vì $a_1 > 0$. Vậy dãy $(a_n)$ tăng và không bị chặn trên, nên $\lim a_n = +\infty$, suy ra $\lim \dfrac{1}{a_n} = 0.$
Mặt khác, $$a_{n+1} - a_n = a_n((1+ a_n^{1-\alpha})^{\frac{1}{\alpha}} - 1) = \frac{f(1/a_n) - f(0)}{1/a_n}$$ với $f(x) = (1+x^{\alpha - 1})^{\frac{1}{\alpha}}$. Ta có $f’(x) = \frac{1}{\alpha} (1+x^{\alpha - 1})^{\frac{1}{\alpha}-1} (\alpha-1)x^{\alpha-2}$. Vì $\alpha > 2$ nên $f’(0) = 0$, hay $$\lim_{x \to 0} \frac{f(x) - f(0)}{x} = 0,$$ suy ra $\lim(a_{n+1} - a_n) = 0$. Theo định lý trung bình Cesàro, ta có $\lim \dfrac{a_n}{n} = 0$.

Đề thiếu, cần thêm giả thiết $m,n \ge 2$ (với $m = 2, n = 1$ thì $F_m | F_n$ nhưng $m \not | n$).

 

Bước 1. Chứng minh rằng $\gcd(F_m, F_{m-1}) = 1$ (quy nạp theo $m$).

Bước 2. Chứng minh rằng $F_{m+k} = F_{k+1}F_m + F_k F_{m-1}$ với mọi $k \ge 1$ (quy nạp theo $k$).

Bước 3. Chứng minh mệnh đề đã cho bằng quy nạp theo $n$.

Xét $n \le m$. Nếu $n < m$ thì $0 < F_n < F_m$ nên $F_m \not | F_n$. Nếu $n = m$ thì hiển nhiên $F_m | F_n$.

Do đó với $n \le m$ thì khẳng định "$F_m | F_n \Leftrightarrow m | n$" đúng.

Xét $n > m$, dùng kết quả Bước 2 cho $k = n - m$, ta được $F_n = F_{n-m+1} F_m + F_{n-m}F_{m-1}$. Do đó $$F_m | F_n \Leftrightarrow F_m | F_{n-m}F_{m-1}  \Leftrightarrow F_m | F_{n-m}$$ (dùng kết quả Bước 1). Giờ áp dụng giả thiết quy nạp cho số $n - m$: $$F_m | F_n \Leftrightarrow F_m | F_{n-m} \Leftrightarrow m | n-m \Leftrightarrow m | n.$$

Bài giảng số học - Đặng Hùng Thắng