Stranger411 nội dung
Có 85 mục bởi Stranger411 (Tìm giới hạn từ 14-05-2020)
#392825 Đếm bằng $v_p$
 Đã gửi bởi
Stranger411
on 03-02-2013 - 15:47
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 03-02-2013 - 15:47
trong
Tổ hợp và rời rạc
Ps: Đang viết 1 bài về $v_p$ và đây là một ứng dụng trong tổ hợp của nó.
#372277 $Q(k) = p^n$
 Đã gửi bởi
Stranger411
on 24-11-2012 - 23:22
trong
Đa thức
Đã gửi bởi
Stranger411
on 24-11-2012 - 23:22
trong
Đa thức
#423590 Chứng minh 3 điểm cùng thuộc một đường vuông góc với $OE'$
 Đã gửi bởi
Stranger411
on 03-06-2013 - 23:15
trong
Hình học
Đã gửi bởi
Stranger411
on 03-06-2013 - 23:15
trong
Hình học
Cho tam giác $ABC$ có $O$ là tâm đường tròn ngoại tiếp, $E$ là tâm đường tròn Euler. Lấy $E'$ thỏa $\widehat{E'BA}=\widehat{EBC}$ và $\widehat{E'AB}=\widehat{EAC}$. Trung trực $OA$ cắt $BC$ tại $A'$. Các điểm $B',C'$ được xác định tương tự. Chứng minh $A',B',C'$ cùng thuộc 1 đường thẳng vuông góc với $OE'$
#438572 Chứng minh ba đường tròn đồng quy
 Đã gửi bởi
Stranger411
on 27-07-2013 - 13:22
trong
Hình học
Đã gửi bởi
Stranger411
on 27-07-2013 - 13:22
trong
Hình học
Cho tứ giác toàn phần $ABCDEF$. Chứng minh các đường tròn đướng kính $AC,BD,EF$ đồng quy tại 2 điểm.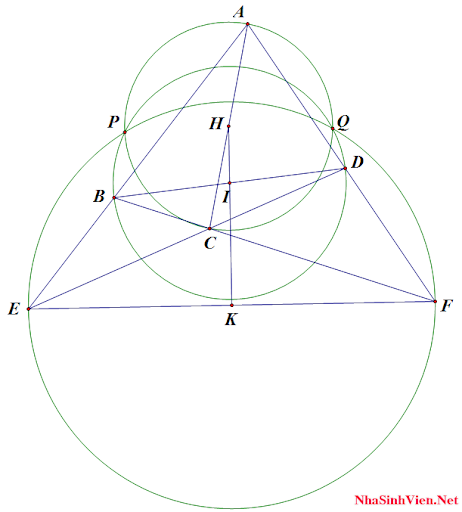
#441489 IMO shortlist 2012 - Problems + Solution
 Đã gửi bởi
Stranger411
on 09-08-2013 - 15:20
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
Stranger411
on 09-08-2013 - 15:20
trong
Thi HSG Quốc gia và Quốc tế
Mới có bản Scan thôi, các bạn dùng tạm ![]()
File gửi kèm
-
 VNMATH.COM-imo 2012 shortlist.pdf 615.93K
1990 Số lần tải
VNMATH.COM-imo 2012 shortlist.pdf 615.93K
1990 Số lần tải
#372273 Phân hoạch tập tốt
 Đã gửi bởi
Stranger411
on 24-11-2012 - 23:13
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 24-11-2012 - 23:13
trong
Tổ hợp và rời rạc
#353030 $p \equiv 1 (\bmod m)$
 Đã gửi bởi
Stranger411
on 08-09-2012 - 23:40
trong
Số học
Đã gửi bởi
Stranger411
on 08-09-2012 - 23:40
trong
Số học
Cho số nguyên tố $p \equiv 1 (\bmod m)$ với $m>2$. Chứng minh:
\[\prod\limits_{i = 1}^p {\left( {{i^{m - 1}} + {i^{m - 2}} + \ldots + i + 1} \right)} \equiv 0 (\bmod p)\]
Bài này dùng 1 tí kiến thức về hệ thu gọn.
Bên mathlink post mấy tháng rồi mà chưa có lời giải :-<
#343066 Chứng minh giá trị của $k$ thuộc 1 tập xác định
 Đã gửi bởi
Stranger411
on 03-08-2012 - 12:48
trong
Số học
Đã gửi bởi
Stranger411
on 03-08-2012 - 12:48
trong
Số học
#340308 $S\left( {{a_n}} \right)$ không chia...
 Đã gửi bởi
Stranger411
on 26-07-2012 - 00:51
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 26-07-2012 - 00:51
trong
Tổ hợp và rời rạc
Chứng minh có vô hạn số $n$ sao cho $S\left( {{a_n}} \right) $ không chia hết cho $5$
#343028 có tất cả bao nhiêu số tự nhiên n<m sao cho m l n(2n+1)(5n+2)
 Đã gửi bởi
Stranger411
on 03-08-2012 - 11:27
trong
Số học
Đã gửi bởi
Stranger411
on 03-08-2012 - 11:27
trong
Số học
\[{\text{m}} = {\text{2}}{007^{2008}} = {3^{4016}}{223^{2008}}\]cho m=20072008 ,hỏi có tất cả bao nhiêu số tự nhiên n<m sao cho m l n(2n+1)(5n+2)
Ta có: $m|n\left( {2n + 1} \right)\left( {5n + 2} \right)$
$ \Rightarrow m|10n\left( {10n + 5} \right)\left( {10n + 4} \right)$ $(1)$
Đặt $10n=x$, ta được: $m|x\left( {x + 5} \right)\left( {x + 4} \right)$
Đặt ${q_1} = {3^{4016}},{q_2} = {223^{2008}}$. Vì $\gcd \left( {{q_1},{q_2}} \right) = 1$
Nên \[{\text{(1)}} \Leftrightarrow \left\{ \begin{gathered}
x\left( {x + 5} \right)\left( {x + 4} \right) \equiv 0(\bmod {q_1}) \\
x\left( {x + 5} \right)\left( {x + 4} \right) \equiv 0(\bmod {q_2}) \\
\end{gathered} \right.\]
Mà $x \equiv 0(\bmod 10)$
Nên $x$ là nghiệm của hệ:
\[\left\{ \begin{gathered}
x \equiv {r_1}(\bmod {q_1}) \\
x \equiv {r_2}(\bmod {q_2}) \\
x \equiv 0(\bmod 10) \\
\end{gathered} \right.\]
với ${r_1},{r_2} \in \left\{ {0; - 4; - 5} \right\}$
Theo định lí Thặng Dư Trung Hoa, hệ có 1 nghiệm $(\bmod 10{q_1}{q_2})$
với mỗi cặp ${r_1},{r_2}$ chỉ tồn tại 1 nghiệm x.
Có tất cả $3^2$ cách chọn ${r_1},{r_2}$ nên có 9 số $x$ thỏa.
Suy ra có 9 số $n$ thỏa mãn bài toán.
#392819 Bất khả quy trên $\mathbb{Z[x]}$
 Đã gửi bởi
Stranger411
on 03-02-2013 - 15:29
trong
Đa thức
Đã gửi bởi
Stranger411
on 03-02-2013 - 15:29
trong
Đa thức
#432488 Hỏi có thể thực hiện dc phép tô màu nói trên hay không nếu: 1.$n= 2012...
 Đã gửi bởi
Stranger411
on 03-07-2013 - 11:37
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 03-07-2013 - 11:37
trong
Tổ hợp và rời rạc
xét số nguyên $n> 1$. Người ta muốn tô màu tất cả các số tự nhiên bởi 2 màu xanh và đỏ sao cho các điều kiện sau được đồng thời thỏa mãn:
i. Mỗi số dc tô bởi 1 màu, và mỗi màu đều dc dùng để tô vô số số;
ii. tổng của n số đôi 1 khác nhau cùng màu là số có cùng màu đó.
Hỏi có thể thực hiện dc phép tô màu nói trên hay không nếu:
1.$n= 2012$
2.$n= 2013$
Tổng quát:
* Nếu $n$ lẻ thì phép tô thực hiện được:
Tô tất cả số chẵn cùng màu đỏ, số lẻ cùng màu xanh. Khi đó, mỗi số được tô bởi đúng 1 màu và có vô hạn lần tô mỗi màu (vì có vô hạn số lẻ, số chẵn). Tổng $n$ số cùng màu là một số cùng màu vì tổng $n$ số lẻ là một số lẻ (vì $n$ lẻ) và tổng $n$ số chẵn là một số chẵn.
* Nếu $n$ chẳn, thì phép tô không thực hiện được:
Phản chứng, giả sử phép tô thực hiện được, suy ra được có vô hạn số được tô bởi 2 màu xanh đỏ.
Khi đó, tồn tại số $a_1$ được tô màu xanh và $b_1 = a_1 +1$ được tô bỏi màu đỏ.
Tiếp tục, cũng tồn tại $b_2 > b_1$ mà $b_2$ được tổ bởi màu đỏ và $a_2$ được tổ bởi màu xanh.
Tương tư như vậy tồn tại $a_{n-1} > a_{n-2}$ được tô màu xanh và $b_{n-1} = a_{n-1} +1$ tô bởi màu đỏ và cũng tồn tại $b_n > b_{n-1}$ mà $b_n$ được tô màu đỏ và $a_n = b_n +1$ tô bởi màu xanh.
Tóm lại các số $a_i$ và $b_i$ là đôi một khác nhau và thỏa $a_i$ màu xanh và $b_i$ màu đỏ và $b_{2k-1} = a_{2k-1} +1$ và $b_{2k} = a_{2k} -1$ với mọi $k \le \frac{n}{2}$
Theo điều kiện đề bài thì gọi $a$ là tổng các số $a_i$ nên a được tô xanh còn $b$ là tổng các $b_i$ nên $b$ được tô đỏ. Nhưng vì $b_{2k-1} = a_{2k-1} +1$ và $b_{2k} = a_{2k} -1$ với mọi $k \le \frac{n}{2}$ nên suy ra $a=b$ từ đó $a,b$ phải được tô cùng màu dẫn tới vô lí.
#312728 Cho $a,b,c>0$và $ab+bc+ca+abc=4$ .CM$a^3+b^3+c^3...
 Đã gửi bởi
Stranger411
on 25-04-2012 - 23:19
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Stranger411
on 25-04-2012 - 23:19
trong
Bất đẳng thức và cực trị
Phải nói đây một bất đẳng thức khá bá đạo.Cho$a,b,c>0$ thỏa mãn $ab+bc+ca+abc=4$.Chứng minh
$a^3+b^3+c^3+9abc\geq 4(a+b+c)$
Nhưng nếu làm bđt nhiều thì cũng không khó gì để nhận ra nó.
Đổi biến $a=\frac{2x}{y+z},b=\frac{2y}{x+z},c=\frac{2z}{x+y} $, ta được $ab+bc+ca+abc=4$
Lời giải còn lại của bài toán các bạn xem trong file đính kèm.
File gửi kèm
-
 Bai 29.doc 548.5K
95 Số lần tải
Bai 29.doc 548.5K
95 Số lần tải
#441245 Mở rộng Problem 4 - IMO 2013
 Đã gửi bởi
Stranger411
on 08-08-2013 - 14:40
trong
Hình học
Đã gửi bởi
Stranger411
on 08-08-2013 - 14:40
trong
Hình học
1 bài mở rộng của thầy Quang Hùng trong GGTH lần 5
Cho tam giác $ABC$, đường tròn $(I)$ đi qua $B,C$ cắt CA,AB tại $N,M$ khác $B,C$.
Đặt $H = BN \cap CM$. Gọi $d$ là đường thẳng qua $I$ vuông góc với $AH$. Lấy $W$ bất kì trên $d$.
$WK,WL$ là đường kính của đường tròn ngoại tiếp các tam giác $WBM,WCN$.
Chứng minh $K,H,L$ thẳng hàng.

#314274 $$\dfrac{a^3+b^3+c^3+3abc}{(a+b+c)(ab+bc+ca)}+\dfrac{abc}...
 Đã gửi bởi
Stranger411
on 04-05-2012 - 13:03
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
Stranger411
on 04-05-2012 - 13:03
trong
Bất đẳng thức - Cực trị
Bài toán của bạn được ghép từ 3 bổ đề sau:Bài toán :
Cho $a, b, c \ge 0$ . Chứng minh rằng :
$$\dfrac{a^3+b^3+c^3+3abc}{(a+b+c)(ab+bc+ca)}+\dfrac{abc}{a^2b+b^2c+c^2a}\ge 1$$
Nguồn : ML
1)${{a}^{3}}+{{b}^{3}}+{{c}^{3}}+3abc\ge \sum{ab\left( a+b \right)}$
2)$\left( a+b+c \right)\left( ab+bc+ca \right)\frac{8}{9}\le \left( a+b \right)\left( b+c \right)\left( c+a \right)$
3)$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{3abc}{2\left( {{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a \right)}\ge 2$
#392813 $a^2 +b | a + b^2$
 Đã gửi bởi
Stranger411
on 03-02-2013 - 14:57
trong
Số học
Đã gửi bởi
Stranger411
on 03-02-2013 - 14:57
trong
Số học
1) $a^2 +b = p^k$ với $k \in \mathbb{Z^+}$
2) $a^2 +b | a + b^2$
ps: mấy chú ở Khtn chắc biết bài này nhỉ
#387048 $P(x^2 -2002) \vdots P(x)$
 Đã gửi bởi
Stranger411
on 15-01-2013 - 22:00
trong
Đa thức
Đã gửi bởi
Stranger411
on 15-01-2013 - 22:00
trong
Đa thức
(1) $degP(x) = 2003$
(2) $P(x^2 -2002) \vdots P(x)$ ($\forall x \in \mathbb{R}$)
ps: hồi chiều làm kiểm tra bị bể bài này
#346443 Các bài toán về số Ferma - Các bài giảng của LEUNG Tat-Wing
 Đã gửi bởi
Stranger411
on 13-08-2012 - 13:46
trong
Tài liệu, chuyên đề, phương pháp về Số học
Đã gửi bởi
Stranger411
on 13-08-2012 - 13:46
trong
Tài liệu, chuyên đề, phương pháp về Số học
Công nhận mấy giáo sư người Tàu rất đáng khâm phục. Mời các bạn tham khảo nó
File gửi kèm
-
 Eng_v7_n4.pdf 57.08K
778 Số lần tải
Eng_v7_n4.pdf 57.08K
778 Số lần tải
#345818 $\frac{{{a^2} - 2}}{{2...
 Đã gửi bởi
Stranger411
on 11-08-2012 - 12:21
trong
Số học
Đã gửi bởi
Stranger411
on 11-08-2012 - 12:21
trong
Số học
#343333 Đếm số cách lát các quân đôminô
 Đã gửi bởi
Stranger411
on 04-08-2012 - 13:57
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 04-08-2012 - 13:57
trong
Tổ hợp và rời rạc
Lát chúng bằng các quân đôminô $1\times2$ sao cho
1) Phủ kín hình chữ nhật và ko có 2 quân nào chồng lền nhau.
2) Vơi $n$ lẻ, ta được phép bổ sung thêm 1 quân đôminô "đặc biệt" sao cho có thể phủ kín ô $n$ và $n+1$
Đếm số cách lát thỏa mãn đề bài.
ps: Thực chất đây là bài toán tập hợp liên quan đến các phần tử tốt.
#346650 ${p_{k + 1}}|{p_1} + {p_2} +...
 Đã gửi bởi
Stranger411
on 14-08-2012 - 11:48
trong
Số học
Đã gửi bởi
Stranger411
on 14-08-2012 - 11:48
trong
Số học
Chứng minh rằng tồn tại 1 bộ hoán vị ${p_1},{p_2}, \ldots ,{p_n}$ của $1,2, \ldots ,n$ sao cho ${p_{k + 1}}|{p_1} + {p_2} + \ldots + {p_k}$ với $k = 1,2, \ldots ,n-1$
#312558 Bất đẳng thức $4$ biến thoả $ abcd=1$
 Đã gửi bởi
Stranger411
on 25-04-2012 - 08:17
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
Stranger411
on 25-04-2012 - 08:17
trong
Bất đẳng thức - Cực trị
Áp dụng bất đẳng thức Tukervici, ta có:Cho các số thực dương $a,b,c,d$ thoả mãn: $abcd=1$.Chứng minh rằng:
$$ 3(a^2+b^2+c^2+d^2) + 4 \ge (a+b+c+d)^2$$
$ 3(a^4+b^4+c^4+d^4) + 4abcd \ge (a^2+b^2+c^2+d^2)^2$
Bất đẳng thức cần chứng minh là dạng tương đương của bất đẳng thức trên. $\blacksquare$
Bất đẳng thức trên dùng pp FMPX để chứng minh.
#343075 MOSP 2001 by Cecil Rousseseau
 Đã gửi bởi
Stranger411
on 03-08-2012 - 13:15
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 03-08-2012 - 13:15
trong
Tổ hợp và rời rạc
Bài này lâu rồi, sử dụng phép chia nhóm là đượcProblem: $a_n$ kí hiệu là số tập con không rỗng của $S$ thỏa mãn rằng:
(i) $S\subseteq${$1$, $2$, $...$, $n$};
(ii) tất cả các phần tử của $S$ đều cung tính chẵn, lẻ.
(iii) mỗi phân tử $k\in{S}$ thỏa mãn $k\geq2|S|$.
Tìm công thức tường minh cho $a_n$
Ta có: $ a_{2m-1}= 2(F_{m+1}-1) $ và $ a_{2m}= F_{m+3}-2 $
với $m\ge1$ và $F_{m}$ là số Fibonacci thứ $m$.
Lời giải:
Đặt $T_{n}=\{S\in\{1,2,\cdots,n\}\}$ thỏa $(ii)$ và $(iii)$
Chia $ T_{n+4} $ thành 3 tập con:
Phần 1: $A_{n+4}=\{S\in T_{n+4}\ ;\ 1,2\notin S,\ \forall k\in S, k\geq 2|S|+2\}$
Xây dựng $ f\ :\ \mathcal{P}(\{1,2,\cdots,n+2\})\rightarrow\mathcal{P}(\{1,2,\cdots,n+4\}) $ thỏa:
$$f(\{x_{1},x_{2},\cdots,x_{k}\}) =\{x_{1}+2,x_{2}+2,\cdots,x_{k}+2\}$$
Ta được: $ f(T_{n+2}) = A_{n+4} $ nên $ |A_{n+4}|=|T_{n+2}|$
Phần 2: $ B_{n+4}=\{S\in T_{n+4}\ ;\ 1,2\notin S,\ \exists k\in S, k < 2|S|+2\} $
Tương tự, ta được:
$f(\phi) =\{3\}$
$f\left( {\left\{ {{x_1},{x_2},...,{x_k}} \right\}} \right) = \left\{ {{x_1} + 4,{x_2} + 4,...,{x_k} + 4,2k} \right\}$
nếu các phần tử cùng chẳn.
$f\left( {\left\{ {{x_1},{x_2},...,{x_k}} \right\}} \right) = \left\{ {{x_1} + 4,{x_2} + 4,...,{x_k} + 4,2k+1} \right\}$
nếu các phần tử cùng lẽ.
Suy ra: $|B_{n+4}|=|T_{n}|+1 $
Phần 3: $ C_{n+4}=\{ S\in T_{n+4}\ ;\ 1\in S\ \mathrm{or}\ 2\in S\} $
Tương tự, ta có: $ |T_{n+4}|=|T_{n+2}|+|T_{n}|+2 $
Từ đó, ta chứng minh được: $ a_{2m-1}= 2(F_{m+1}-1) $ và $ a_{2m}= F_{m+3}-2 $
#343069 bài toán về tập tốt
 Đã gửi bởi
Stranger411
on 03-08-2012 - 12:53
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 03-08-2012 - 12:53
trong
Tổ hợp và rời rạc
#392817 $c \le \frac{1}{4n}$
 Đã gửi bởi
Stranger411
on 03-02-2013 - 15:17
trong
Dãy số - Giới hạn
Đã gửi bởi
Stranger411
on 03-02-2013 - 15:17
trong
Dãy số - Giới hạn
1) $a_n =0$
2) $a_k = c+ \sum_{i=k}^{n-1}(a_i + a_{i+1})$ $\forall k=\overline{0,n-1}$.
Chứng minh $c \le \frac{1}{4n}$
- Diễn đàn Toán học
- → Stranger411 nội dung


